地震作用下建筑抗震支吊架体系的动力放大系数研究
董逸轩,丁幼亮,2,3, 朱浩樑 ,2,3
(1.东南大学土木工程学院,南京210096;2.江苏建筑机电抗震研究院,南京211200;3.南京睿永智运维工程科技有限公司,南京211200)
1 引言
地震是一种常见的自然灾害,强度大、范围广,发生频率高,并且难以预测,给人类的生命财产安全造成极大的损害。我国是地震灾害频发的国家,也是地震造成生命财产损失最大的国家之一,根据不完全统计,全球由于地震死亡的人数中,我国约占50%。随着各国对建筑抗震的重视程度不断提高,抗震规范愈加严格,结构抗震能力在得到保证的同时,建筑机电抗震设计领域开始引起人们的重视。建筑抗震支吊架在地震中对建筑机电设施给予可靠保护,承受来自任意水平方向的地震作用【1】。因此,准确计算建筑抗震支吊架的地震作用是抗震支吊架设计的基础问题。
依附于建筑主体结构之上的抗震支吊架体系是典型的二次结构体系。目前为止,等效侧力法、楼面反应谱法和时程分析法是用于计算二次结构地震反应的主要方法。3种计算方法各有优缺点,为了建立简便适用的支吊架地震作用计算方法,就必须准确把握主体结构与支吊架体系之间的动力作用特征。抗震支吊架体系的动力放大系数是表征主体结构对二次结构动力影响的重要参数。为此,本文针对多层建筑和高层建筑研究不同自振周期的支吊架体系的动力放大系数,讨论场地类别和安装楼层对动力放大系数的影响规律。
2 抗震支吊架计算方法对比
抗震支吊架的构成包括加固吊杆、斜撑、锚固体和抗震连接构件等【2】。抗震支吊架与结构体牢固连接,承受地震中任意水平方向的地震作用,保护机电设备管线不受地震破坏,并防止出现机电设备受损造成的二次灾害。抗震支吊架及机电设备管线可以简化为附属于建筑主体结构的单质点体系。
等效侧力法是GB 50981—2014《建筑机电抗震设计规范》推荐的地震作用计算方法,本质是拟静力分析方法。据已有研究,等效侧力法在附属结构基本周期为0.06s到1.4倍建筑物基本周期范围时计算结果偏小,而当附属结构周期较小时计算结果则偏大【3】。此计算方法在计算精度上尚需完善。时程分析法可以较准确地计算地震波输入下主体结构和附属结构的地震响应,但计算量巨大,并且时程分析法的计算结果一般离散程度较大,在实际工程应用不够便利高效也是时程分析法的问题之一。
楼面反应谱是安装在某楼面上的具有不同自振周期和阻尼的单自由度系统对楼面地震反应时程历史最大值的均值组成的曲线【4】。楼面反应谱法按照发展阶段可以分为传统反应谱法和新型反应谱法。传统反应谱法不考虑主体结构和附属结构的相互作用,将其强行解耦,先计算主体结构在地震下的响应,再将附属结构与主体结构连接处的响应作为附属结构的输入进行计算。传统反应谱法由于不考虑主体结构与附属结构的相互作用,计算结果会产生较大误差。新型反应谱法考虑了主体结构和附属结构的耦合作用,计算结果较传统反应谱法更加精确,在附属结构周期较长且质量占主体结构较大的情况下传统楼面反应谱法有较高的精度【5】。但由于楼面反应谱建立过程复杂,且理论上一次建立只能针对于特定建筑的单个楼层,因此楼面反应谱法在工程应用中的普适性有所欠缺。在实际工程中,建筑抗震支吊架体系的自振周期一般较小,为了建立适用于抗震支吊架地震作用计算的简化楼面反应谱法,本文重点研究多层建筑和高层建筑研究不同自振周期的支吊架体系的动力放大系数,为后续研究简化楼面反应谱法提供了基础依据。
3 工程实例分析
3.1 模型建立
本文采用ETABS软件建立主体结构-抗震支吊架耦合作用模型。模型均采用空间杆系单元对框架梁、柱进行模拟,采用板单元对楼板和剪力墙进行模拟。在建筑结构每一层设置抗震支吊架,抗震支吊架设置于楼层加速度最大处,用以模拟地震作用下的最不利工况。采用时程分析法分别计算楼层的绝对加速度和抗震支吊架的绝对加速度。选取地震波时,地震波加速度时程的最大值符合GB 50011—2016《建筑抗震设计规范》的规定,并且弹性时程分析时,每条时程曲线计算所得结构底部剪力应不小于振型分解反应谱法计算结果的65%,多条时程曲线计算所得结构底部剪力的平均值不应小于振型分解反应谱法计算结果的80%。
3.2 算例工况
以某5层框架结构和21层框架-剪力墙结构为例,抗震支吊 架 的 自 振 周 期 分 别 为0.02s、0.05s、0.08s、0.10s、0.15s和0.20s。分别计算在Ⅰ、Ⅱ、Ⅲ、Ⅳ类场地土条件下各楼层楼面的绝对加速度和抗震支吊架的绝对加速度。抗震设防烈度为7度(0.1g),设计地震分组为第Ⅱ组。图1和图2分别为5层框架结构和21层框架-剪力墙结构的整体分析模型,分别在4类场地土下各选取7条地震波,地震波加速度峰值控制在GB 50011—2010《建筑抗震设计规范》规定范围之内。

图1 5层框架结构模型

图2 21层框架-剪力墙结构模型
计算结果取7条地震波的平均值,并计算抗震支吊架绝对加速度与楼层绝对加速度的比值,即地震作用下抗震支吊架的动力放大系数,计算结果见表1~表8。

表1 5层框架结构在Ⅰ类场地下的动力放大系数

表2 5层框架结构在Ⅱ类场地下的动力放大系数

表3 5层框架结构在Ⅲ类场地下的动力放大系数

表4 5层框架结构在Ⅳ类场地下的动力放大系数

表5 21层框架-剪力墙结构在Ⅰ类场地下的动力放大系数
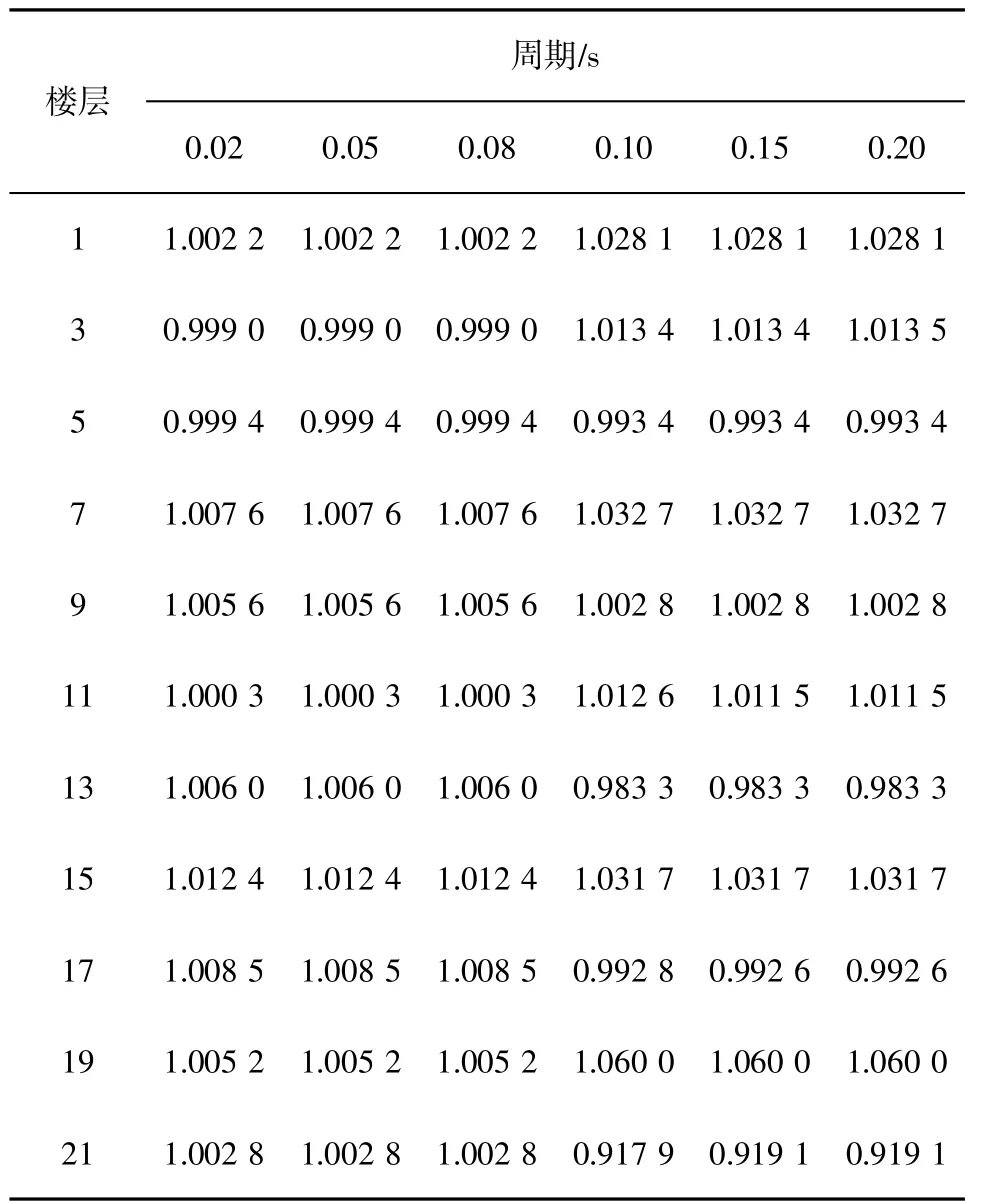
表6 21层框架-剪力墙结构在Ⅱ类场地下的动力放大系数

表7 21层框架-剪力墙结构在Ⅲ类场地下的动力放大系数
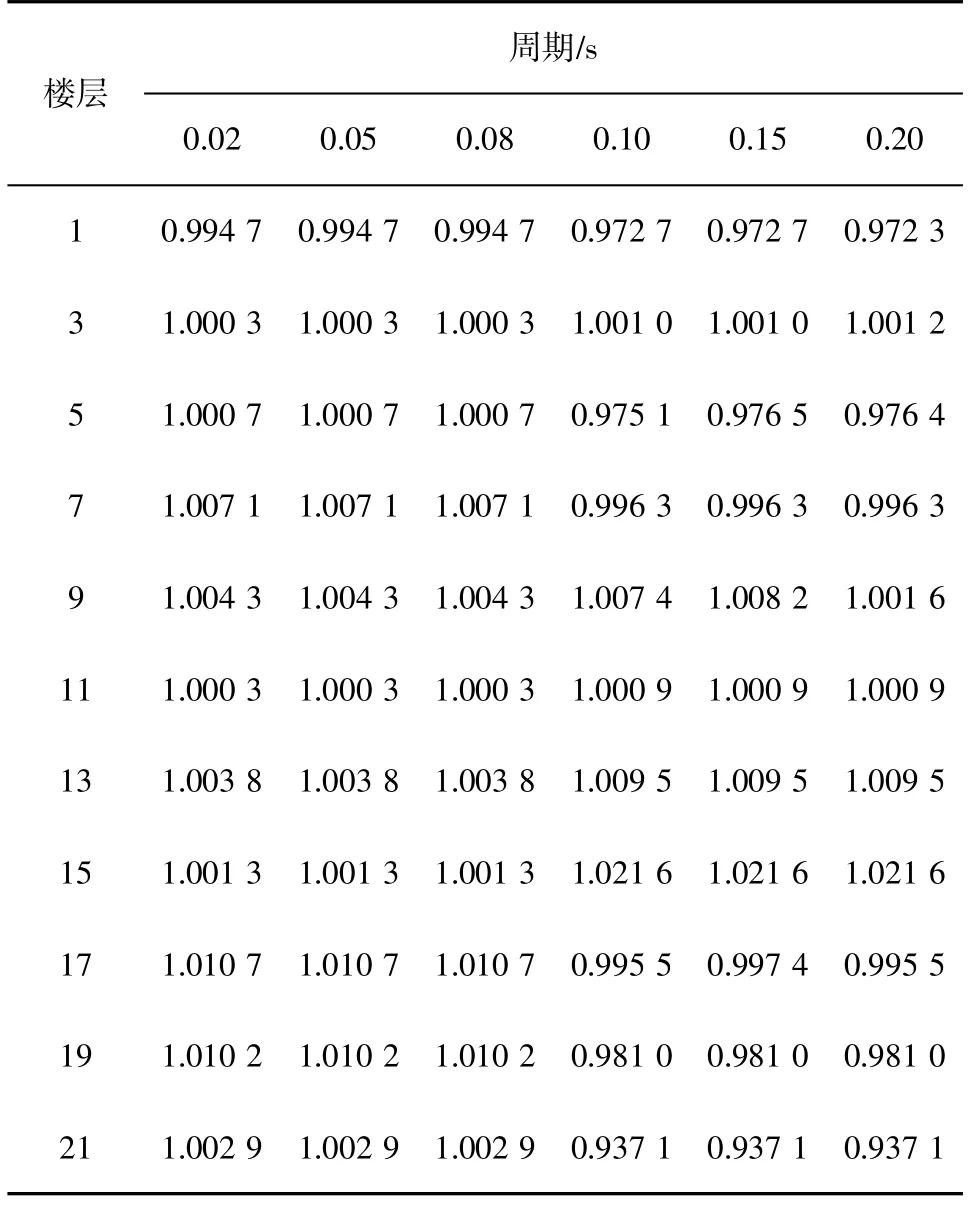
表8 21层框架-剪力墙结构在Ⅳ类场地下的动力放大系数
从表1~表4可以看出:
1)抗震支吊架自振周期小于0.10s时,5层框架结构在I、II、III和IV类场地条件下各楼层的动力放大系数最大值分别为1.003、1.001 7、1.002 3和1.003 1。可以看出,动力放大系数非常小,可以忽略。此外,随着场地类别的增大,动力放大系数最大值有增大的趋势,但因为动力放大系数很小,场地类别的影响也可以忽略。
2)抗震支吊架自振周期介于0.1~0.2s时,5层框架结构在I、II、III和IV类场地条件下各楼层的动力放大系数最大值分别为1.099 5、1.055 7、1.056 3和1.080 5。可以看出,动力放大系数最大值不超过1.10。此外,场地类别对动力放大系数的影响规律不明显。
从表5~表8可以看出:
1)抗震支吊架自振周期小于0.10s时,21层框架-剪力墙结构在I、II、III和IV类场地条件下各楼层的动力放大系数最大值分别为1.009 7、1.012 4、1.010 1和1.010 7。可以看出,动力放大系数非常小,可以忽略。此外,场地类别对动力放大系数的影响规律不明显。
2)抗震支吊架自振周期为介于0.1~0.2s时,21层框架-剪力墙结构在I、II、III和IV类场地条件下各楼层的动力放大系数最大值分别为1.116 8、1.06 0、1.056 9和1.021 6。可以看出,动力放大系数最大值不超过1.12。此外,场地类别对动力放大系数的影响规律不明显。
上述分析结果总体来看,场地类别和楼层位置对于动力放大系数没有显著影响,抗震支吊架的动力放大系数总体较小,根据动力放大系数和楼层的绝对加速度近似计算抗震支吊架的绝对加速度,可以简化计算抗震支吊架的地震作用,从而为建立抗震支吊架地震作用计算的简化楼面反应谱法提供了基础依据。
4 结语
1)抗震支吊架自振周期小于0.10s时,地震作用下支吊架绝对加速度相对于楼层绝对加速度的放大系数不超过1.03,动力放大系数可以忽略;
2)抗震支吊架自振周期介于0.1~0.2s时,动力放大系数的波动性较大,但最大值仍不超过1.12,动力放大系数仍较小;
3)场地类别和楼层位置对于动力放大系数没有显著影响,因此,根据动力放大系数和楼层的绝对加速度可以简化计算抗震支吊架的地震作用,从而为建立抗震支吊架地震作用计算的简化楼面反应谱法提供了基础依据。

