贯流风机不同湍流模型数值模拟时的应用效果分析

珺，程家胜，舒朝晖

（1.华中科技大学，武汉 430074；2.武汉理工大学，武汉 430070）

0 引言

贯流风机作为家用分体壁挂式空调室内机的核心送风部件，其送风性能和噪声大小受到广大消费者和研究人员的关注。贯流风机在工作时，流体从叶轮一侧进入内部流场，从另一侧穿出叶轮，在叶轮内侧靠近蜗舌的位置存在明显的偏心涡结构，偏心涡的存在对于贯流风机的气动性能有明显的影响［1-2］。

自从20世纪50年代Eck［3］提出贯流风机后，一系列有关的试验相继展开，许多学者结合试验和可视化技术对贯流风机的内部流场进行研究［4-7］。随着计算流体动力学的发展， CFD等模拟软件广泛被用于流场模拟与仿真计算，这给贯流风机的研究也带来了极大便利。国内外许多研究者通过FLUENT等流体仿真软件对贯流风机的内部流场和噪声性能进行了研究［8-10］。在贯流风机的模拟计算中，可以选用的湍流模型有多种，最常用的有雷诺平均方法（RANS）和大涡模拟（LES）。RANS方法将非稳态的N-S方程对时间取平均，求解得到流场的时均结果。针对雷诺平均方法，邢改兰等［11］对比了RNG k-ε模型和Standard k-ε模型，认为RNG k-ε模型计算时的收敛速度更快，预测的叶轮内部旋涡强度更大。LES模型将N-S方程在小空间域内取平均，把流场中的涡分为大小尺度的2种，大涡直接求解，小涡则通过亚网格尺度模型求解，该模型有在计算噪声时具有较高精度，但同时对网格的尺寸和质量要求较高。舒朝晖等［12］对比了RNG kε、RSM、DES、LES 4种湍流模型在计算贯流风机流场时的差异，结果表明DES与LES模型在捕捉流场的微小流动细节方面更有优势，但对网格要求较高且耗用的计算资源更多。SAS模型由Menter［15］提出，它结合了RANS和LES两种模型的思想，稳态区域的计算类似于RANS模型，而不稳定流动区域的计算则类似于LES模型，但是该模型不需要和网格关联，能够自动调整解析小尺度涡，对网格尺寸的依赖相比LES模型低，并且有研究表明该模型在流场噪声的计算上有着不错的精度［16］。

本文通过建立贯流风机流场的二维模型，采用计算流体力学的方法，针对RNG k-ε、LES、SAS这3种湍流模型的模拟结果进行对比，分析使用不同的湍流模型在计算贯流风机内流场和噪声等性能时的差异，为实际应用提供参考。

1 数值模型

1.1 物理模型

本研究所用的物理模型由厂家提供，简化后的模型如图1（a）所示，主要包括换热器和贯流风机（蜗壳、蜗舌、叶轮），其中叶轮采用非等距叶轮，叶片数为35。由于贯流风机轴向具有一致性，因此本研究采用二维模型进行模拟计算。二维整体流场模型如图1（b）所示，整体计算域呈半圆形，该半圆半径为10倍叶轮外径。

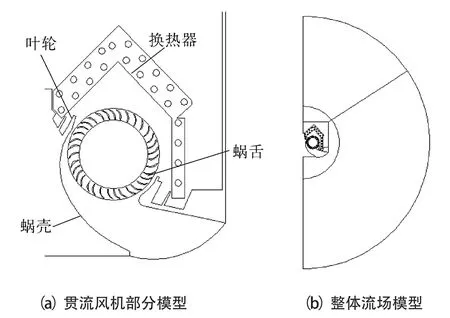
图1 室内机物理模型

1.2 网格划分

本文的3种湍流模型采用相同的网格尺寸进行计算，整体计算域的网格如图2（a）所示，外部环形区域流场的网格采用结构网格，如图2（b）所示。贯流风机及内流区域采用非结构网格，如图2（c）所示。为使模拟结果更加精确，针对叶轮壁面设置边界层，并且加密蜗壳和蜗舌附近的网格，图2（d）示出带有边界层的叶轮处网格。

图2 网格模型

1.3 模拟条件设置

本研究采用FLUENT软件进行计算，为了缩短计算时间，先统一使用RNG k-ε模型进行稳态计算，叶轮区域设置为Frame Motion，速度压力耦合采用SIMPLE算法；再用稳态计算的结果作为3种湍流模型非稳态计算的初始值，叶轮区域设置为Mesh Motion，速度压力耦合采用PISO算法，时间步长设置为0.000 2 s，取计算达到准稳态（以监测的出口流量与蜗舌处压力等参数出现周期性变化作为依据，本文取1.2 s，总共6 000个时间步长）时的流场作为计算结果来分析。边界条件设置如下：进出口为压力进出口，表压均为0 Pa；换热器区域设置为多孔介质和管束组成的区域；旋转区域与静止区域之间设置Interface边界加以连接；叶片壁面设置为旋转壁面；叶轮转速设为1 200 r/min；流体介质为空气，采用FLUENT软件中的默认参数。

1.4 网格无关性验证

网格无关性验证的目的是在保证数值模型准确的前提下尽可能减少计算量，达到节省计算资源的效果。根据不同的网格加密尺度，本文共选取5组网格进行无关性验证，以使用RNG k-ε模型计算达到准稳态时的出口流量作为参考指标进行比较，网格数量及对应的出口流量见表1。由表可知，网格数量从mesh-1增加到mesh-3时，出口流量随之增加，而继续增加到mesh-4、mesh-5时出口流量的变化很小，也即网格数量的增加对结果影响很小。为了减少计算量，本文统一采取mesh-3对应的网格进行数值模拟。

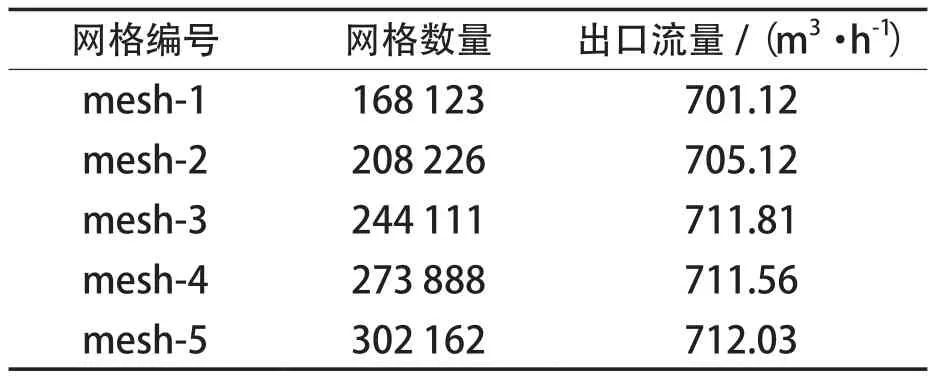
表1 不同网格数量对应的出口流量

2 结果分析

2.1 计算过程对比

在使用FLUENT软件进行非稳态计算时，需要保证在每个时间步长内达到收敛。本文计算时每个时间步长的最大迭代步数设置为60步，3种湍流模型在计算时均能在60步以内达到收敛。对比计算速度，如表2所示，其中RNG k-ε模型在计算时，每一个时间步长一般需要迭代48～50次达到收敛，LES模型一般需要迭代32～34次达到收敛，而SAS模型只需要迭代29～31次就能达到收敛。在总共6 000个时间步长的计算过程中，RNG k-ε模型计算时总共迭代294 494步（包含稳态计算的5 000步，下同），LES模型总共迭代206 523步，SAS模型则只迭代了188 674步。由此可见，这3种模型在计算过程中，SAS模型计算效率最高，LES次之，RNG k-ε模型偏低。

表2 不同湍流模型计算过程中的计算速度对比

在非稳态计算的过程中，本文对实时的出口流量和蜗舌处的压力进行了监测，波动曲线分别如图3，4所示。由图3可知，使用RNG k-ε模型计算时，出口流量的波动性最小，在0.4 s左右就已经只在一个很小的范围内波动，数值近乎稳定；SAS模型的波动较为明显，但整体在720～740 m3/h区间内上下波动，出口流量的平均值比RNG k-ε模型高；而LES模型的波动相比前两者更加明显，波动幅值更大，但出口流量的平均值要低于前两者。由图4可知，3种模型监测的静压均在一定的范围内上下波动，但RNG k-ε模型的波动性最小，幅值较小，周期性最明显；LES模型的波动范围最大，周期性最弱，且压力的平均值最低。因此，在获取出口流量和静压等流场数据指标时，尤其在进行性能优化时，使用RNG k-ε模型更加方便，各组数据间进行对比时的误差最小。

图3 出口流量随计算时间波动曲线

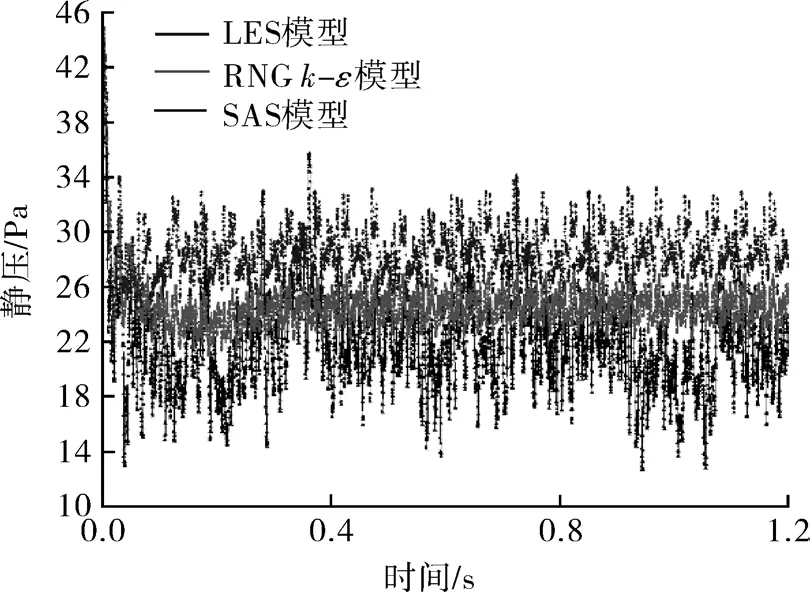
图4 蜗舌壁面静压随计算时间波动曲线

2.2 内流场对比

使用3种湍流模型计算得到流场的静压云图与速度云图分别如图5和6所示，在靠近蜗舌的一侧3种湍流模型都存在明显的偏心涡，叶轮进口与偏心涡部分都属于低速区，而高速区都集中在叶轮出口处。其中LES模型相比另外两种模型偏心涡的范围更小，且叶轮出口处的气体流速相对较小，考虑到这是流场一个瞬间（1.2 s）的静压/速度云图，结合图3中显示的LES模型计算时瞬时波动幅度最大，且出口流量值始终低于另外两个模型，由此可以解释其偏心涡区域和叶轮出口流速比另外两种模型小。RNG k-ε模型计算得到的云图中静压与速度整体分布均匀，具有时均特性，对比图5可以发现，另外两种模型在叶轮进口处均存在一些不规则的高压微团，LES模型中甚至出现了低压微团；而对比图6可以发现，LES和SAS模型在偏心涡处出现了多个低速旋涡，并且在叶轮进口与出口流道均出现了一些高速流体微团，说明LES和SAS模型在捕捉流场内微小尺度流动方面明显优于RNG k-ε模型。

图5 3种湍流模型对应的静压云图

图6 3种湍流模型对应的速度云图

2.3 噪声对比

由于RNG k-ε模型是使用雷诺平均方法计算得到时均流场，不能用于计算气动噪声，因此本文只对比LES与SAS模型在噪声计算上的差异。噪声计算采用FW-H方程，本文在计算6 000个时间步长，即达到准稳态后开启FW-H方程，设置声源与噪声接收点（噪声接收点采取GBT7725-2004空调器性能标准进行设置），继续计算800个时间步长，并对结果进行对比分析。

图7是选择不同声源（叶轮、蜗壳、蜗舌以及以三者同时作为声源，转速为1 200 r/min）情况下两种湍流模型的总声压级对比，从中可以看出，2种湍流模型在以蜗舌为声源时得到的总声压级最低，而在以蜗壳、叶轮以及三者同时作为声源时总声压级依次升高，且LES模型的总声压级略高于SAS模型。

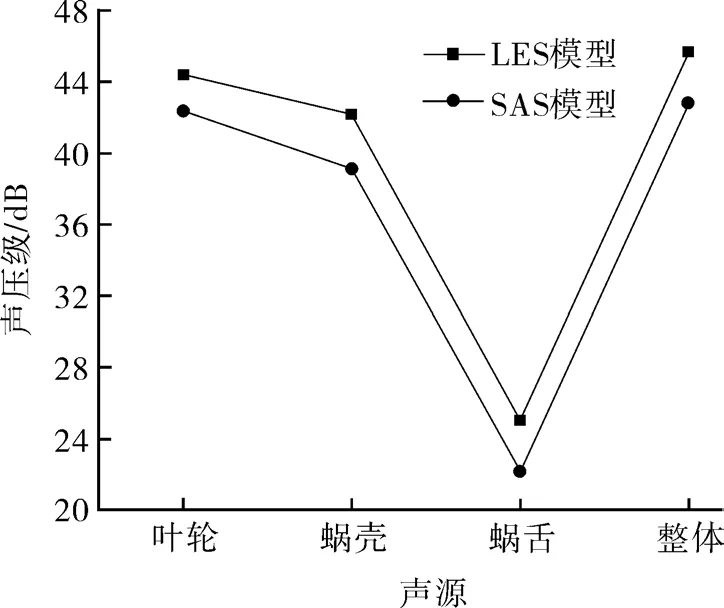
图7 不同声源对应的总声压级

图8示出在不同叶轮转速（以叶轮为声源）工况下2种湍流模型的总声压级对比，由图可知，LES模型的总声压级始终略高于SAS模型，但2种湍流模型计算的总声压级均随着转速增加近似呈线性地增加，变化规律基本一致。

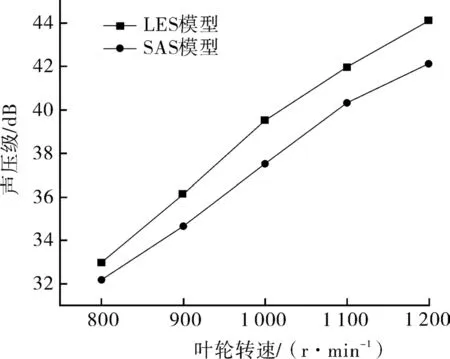
图8 不同转速对应的总声压级

图9示出2种湍流模型以叶轮为声源输出的噪声频谱图，从图中可以看到2种湍流模型在基频（1 200×35/60=700 Hz）及其谐波频率（1 400 Hz、2 100 Hz）处均存在明显的尖峰，这符合叶轮辐射的旋转噪声的离散特性。除此之外，2种湍流模型的声压级随频率变化的整体趋势基本一致，低频时声压级较高，随着频率升高声压级逐渐衰减。

图10示出2种湍流模型以叶轮、蜗壳和蜗舌同时作为声源输出的噪声频谱，从图中可以看到，两种湍流模型在基频处均能看到明显的尖峰，而在谐波频率处的尖峰不明显，整体呈湍流噪声特性，没有明显的离散特性；在变化趋势上，2种湍流模型的声压级均随频率增大而降低，且基频以下的低频段声压级较高。因此，可以认为2种湍流模型对于噪声的预测结果十分接近。

图9 叶轮作为声源时的噪声频谱

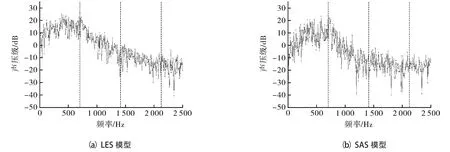
图10 叶轮、蜗壳、蜗舌同时作为声源时的噪声频谱

3 结论

（1）使用3种湍流模型进行计算时，SAS模型的计算速度最快，单个时间步长内收敛所需的迭代步数最少，LES模型次之，RNG k-ε模型计算速度最慢，单个时间步长内收敛所需的迭代步数最多。

（2）用3种湍流模型在计算中监测流量与压力时，RNG k-ε模型监测的数据波动最小，接近稳定，SAS模型监测的数据总体在一定范围内波动，而LES模型监测的数据波动最为明显，周期规律性最弱。

（3）RNG k-ε模型计算得到的云图中静压与速度整体分布均匀，具有时均特性，而LES与SAS模型则具有明显的瞬时特性，在捕捉流场内微小尺度流动方面较RNG k-ε有优势。

（4）SAS模型计算得到的总声压级略低于LES模型，但其随声源和叶轮转速变化的规律与LES模型高度一致，且两者噪声频谱图的整体衰减趋势十分接近，符合叶轮旋转噪声的离散特性。

整体而言，RNG k-ε模型计算流场的性能数据时最稳定，非稳态误差小，而LES模型与SAS模型则能有效捕捉流场中的微小尺度流动，其中SAS模型对网格质量要求较低，但对于气动噪声的计算结果与LES模型十分接近。在实际数值模拟时，可以针对不同的条件和要求来选择不同的湍流模型。