考虑底部过流的透水框架群阻力系数研究

刘建华，杨中华，李 达，李 明

(1. 武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2. 长江航道规划设计研究院，湖北 武汉 430040)

四面体透水框架是近年来得到广泛应用的一种“亲水性”生态护堤固岸、防护墩柱技术，其结构基本形式为6根相同的钢筋混凝土支架拼接而成的正四面体，内部空心可透水。四面体透水框架施工简单、成本较低，特殊的结构使得其减速促淤效果明显、适应河床变形能力强，优良的透水性减小了对水生动植物与陆地生态循环的影响，是一种多功能生态技术[1-2]。目前透水框架的研究偏向于防冲促淤、减速效果等的定性分析研究。徐国宾等通过室内试验分析透水框架群减速落淤和防护效果，并探讨其布设的密疏度、框杆断面形式和长宽比以及框架群空间布设尺度对减速率的影响[3]；杨中华等利用PIV研究四面六边透水框架周边流场性质，结果表明背流布置与迎流布置相比减速效果更好[4]；Wang等从流速分布、水深和阻力系数等方面探究清水过流条件下透水框架对河道保护作用[5]。

框架群的铺设加大了河道阻力，在河道水力计算中需要考虑其阻水作用。目前对于透水框架阻力大小的理论研究存在不足。已有研究大多针对其水力特性展开，涉及阻力系数计算方面研究少。李若华通过水槽试验数据拟合建立计算式，但无严密的理论分析[6]。阻力系数法是量化河床床面阻力大小的最常见方法，当床面粗糙度较小时，可以将其对水流的影响等效视为河床阻力，得到床面阻力系数与粗糙高度的关系[7]；但当河床床面的粗糙度很大，影响到水流过水面积的情况下，传统的阻力系数与粗糙高度的关系式不再满足。已有研究忽略大尺度的粗糙结构体底部过流量，得出不考虑底部透水情况下的阻力系数与粗糙高度的关系式[8-10]。而在实际河道中，对于透水框架这类大尺度粗糙结构体，形态结构往往使其内部具备一定透水能力，这种情况下透水框架的阻力系数计算式有待进一步研究[11]。

对于有底部透水层的流动问题，当前研究主要是将流动进行分区，提出了多种流速分层理论[12-13]。利用分层理论求解断面的平均流速需要对每一层流速分布分别求解，所用方法较为复杂，难以直接应用到河道过流能力的计算中。同时，粗糙体排列方式、底层透水量的计入也增加了问题的难度。因此，本文将从建立考虑底部过流的透水框架河床粗糙系数的角度出发，将透水框架视为大尺度的粗糙结构体，考虑大尺度粗糙体内部过流流量，基于已有的流速分层理论，结合透水框架的结构性质，提出透水框架阻力系数与相对粗糙特征高度之间关系的计算式。

1 大尺度粗糙结构体特征高度理论

利用边界层理论和混合层理论研究底部透水条件下的水流特性，主要特征高度包括当量粗糙度、 零平面位移和入侵深度等特征高度。当量粗糙度用来概化床面粗糙高度，一般认为其大小与河床颗粒粒径及级配有关[14]。零平面位移用来描述理论河床下降后的高度位置，表征粗糙体吸收动量的平均位移，常用粗糙体与水流接触面流速廓线由高向低延伸至流速为0处高度表示[15-17]。不考虑底部过水时，在相对淹没深度较小条件下，Bayazit[8]利用对数分布律求出与关系。粗糙结构体在高度处与自由水面接触，此处紊动切应力最大，在零平面位移高度处切应力达到最小，与混合层理论中入侵深度物理意义类似[18]。

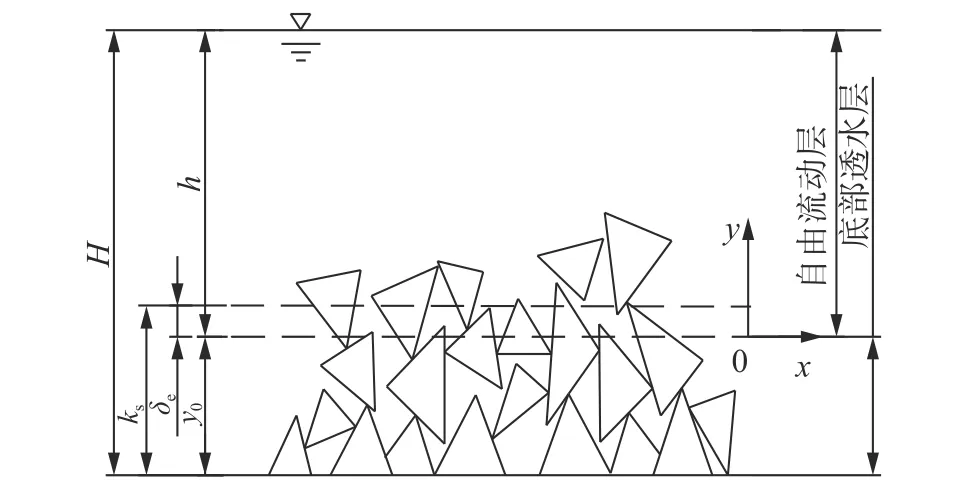
图 1 双层模型示意Fig. 1 Two-layer model diagram

2 考虑粗糙结构体底层透水的阻力系数公式推导

根据分层理论，对上部自由流动层和底部透水层分别计算。

在底部透水层中，水体流动受到水重力的分力、切应力和粗糙结构体产生的拖曳力的影响。入侵深度以下的水体，切应力可以简单视为0，线性动量守恒，此时为重力分力与拖曳力之间的平衡。因此，对于均匀流条件下的底部透水层，根据动量方程得：

式中：N为形状系数，与粗糙体结构种类有关。Cheng[9]在不考虑底部透水情况下利用边界层理论研究大尺度粗糙体阻力系数时，证实当零面位移高度取值合适，上层的有效阻力系数可用式（5）求出。Li[12]利用混合层理论分析一定植被密度条件下的刚性植被过水的试验数据，得出上层自由流动层阻力系数计算满足式（5）。本文也将式（5）作为上层流动的阻力系数计算式。将式（5）与（4）联立，得：

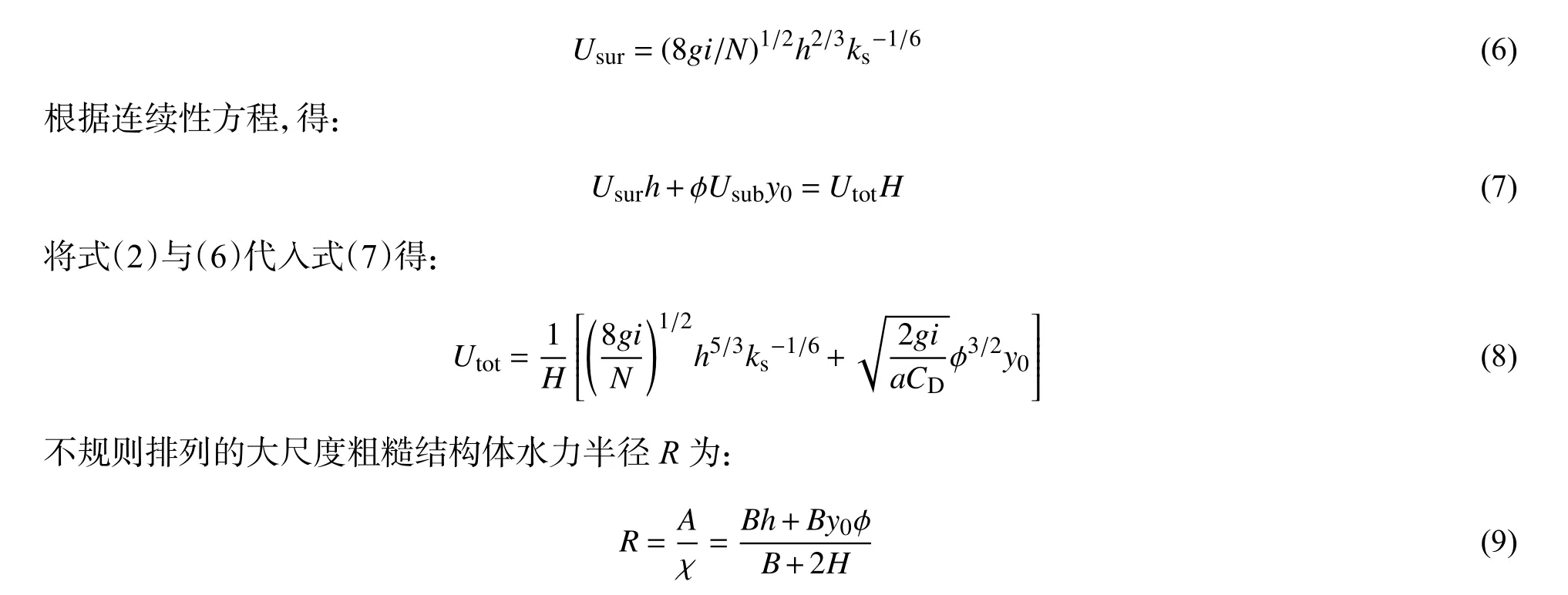
3 四面体透水框架过流条件下参数确定和公式验证

3.1 试验概况

试验在Armfield公司生产的高精度变坡水槽中进行，试验装置如图2，水槽长7.50 m，宽0.30 m，高0.45 m。流量范围为0～30 L/s，坡度为0～2%，用于测量精度要求较高的明渠流动试验。水深及框架平均高度由探针测量，精度为0.1 mm。

试验中的透水框架有4种型号（表1），模型几何比尺为20。模型满足几何相似和水流运动相似（含流态相似）。共有6种铺设类型，铺设长度均为7 m。其中3种铺设选取单一类型（型号4）框架铺设，另外3种使用混合类型（包含所有型号）的框架铺设，单一类型框架两种铺设与混合类型框架2种铺设的框架体体积相同。调整坡度分别为0.001与0.002，同时设置流量为6～13 L/s。实际设定工况共计47组。利用探针测量水深与框架体平均高度。PIV用于测量均匀流条件下框架上层断面流速，进而计算底部透水量。

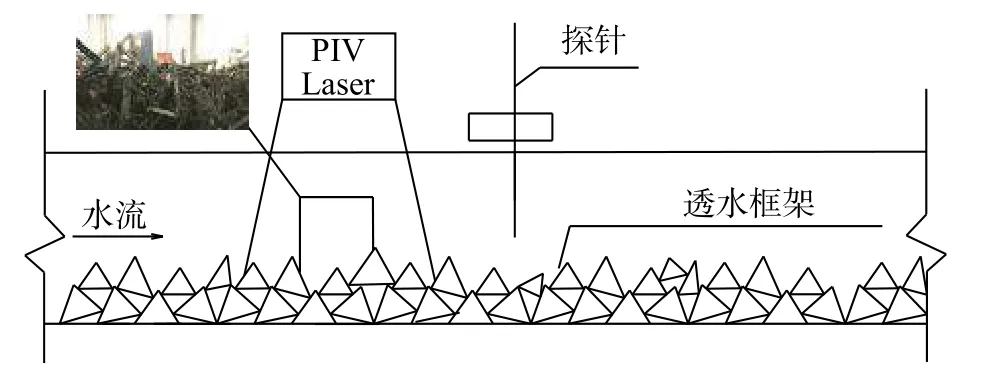
图 2 试验装置示意Fig. 2 Experimental set-up

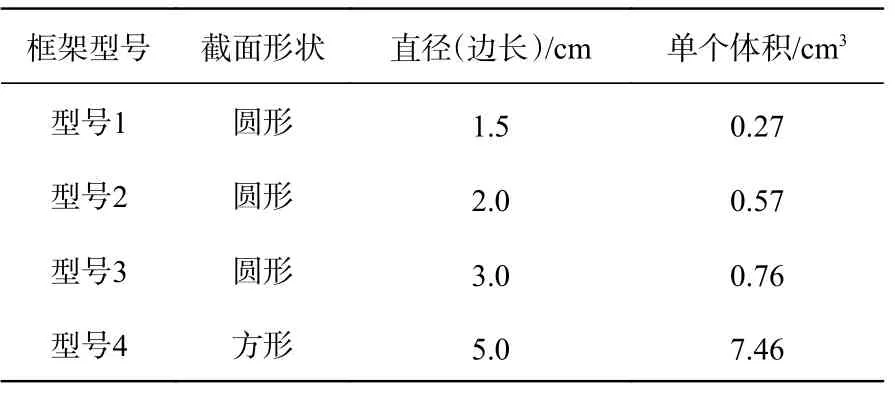
表 1 框架尺寸Tab. 1 Frame size

3.2 数据分析

3.2.1 流速分布 框架铺设前，水深方向上断面流速分布呈“J”型，黏滞力使得流速在水层上部减小速率缓慢，随着水深减小，流速减小速率逐渐增大；框架群铺设后，水深方向上断面流速分布呈“S”型，黏滞力使得框架群上部水层流速减小缓慢，由于框架群的阻力作用，在近框架群位置，流速减小速率增大（见图 3）。

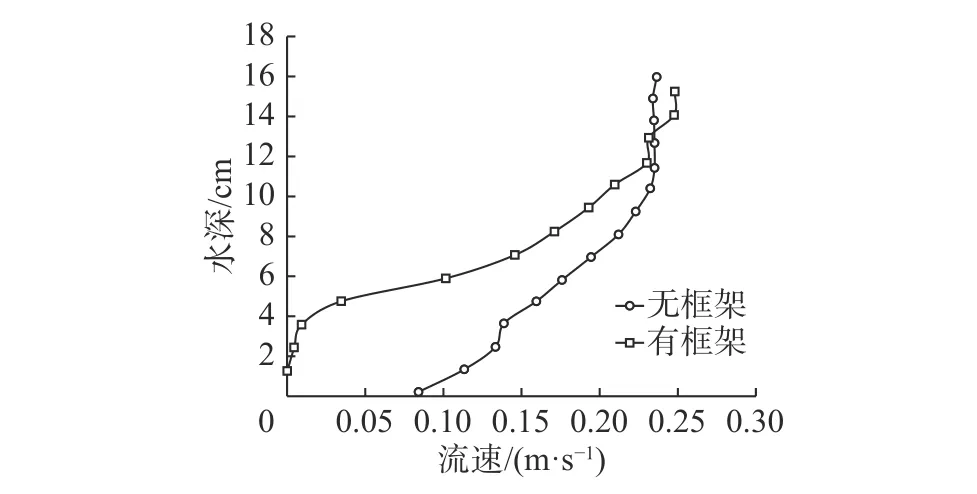
图 3 有无框架条件下断面流速分布（Q=8 L/s）Fig. 3 Velocity distribution with and without frames （Q=8 L/s）

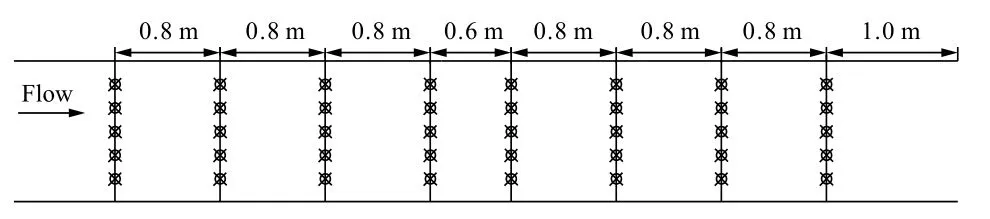
图 4 框架高度测量点示意Fig. 4 Measurement for the average height of frames

3.2.2 阻力系数公式 目前已有文献对透水框架当量粗糙度没 有准确的定义方式，的 大小与框架本身的特征长度、投放框架类型等有关。框架群平均高度表征结构体高度平均化，测量通过探针法实现，均匀铺设一组密度下的框架群后，通过探针分别测出水槽中测量点与框架接触点高程和槽底高程，接触点高程减去槽底高程即可推算出该点处框架的高度。本试验在水槽方向上选取8个测量断面，分别距出水口 1.0，1.8，2.6，3.4，4.0，4.8，5.6 和 6.4 m。每个断面选取的测量点分别距右岸 0.05，0.10，0.15，0.20和0.25 m，共计40个测量点，取均值记为框架平均高度，如图4所示。

高柱等[20]研究得出单一贴壁四面体透水框架拖曳力系数与雷诺数变化关系曲线，考虑的雷诺数范围为 1 800～155 000，本试验雷诺数范围为 25 000～50 000，取数值为 1.567。将式（11），（12）和取值代入式（7）可得：

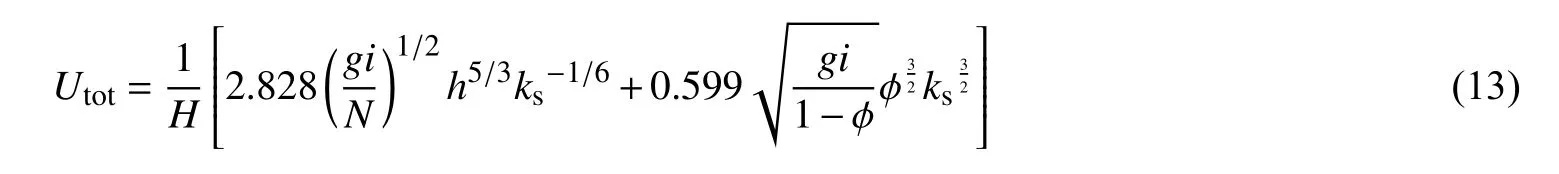
4 结 语

本文针对大尺度粗糙结构体实际底部过流情况，概化提出新的双层流速分布形式。基于该理论，得出考虑大尺度粗糙结构体在占用过水面积、同时底部透水层不可忽略透水量情况下的阻力系数计算式。通过调整形状系数，透水框架群试验数据与推导式配型良好，最终得出考虑底部过流条件下透水框架群阻力系数计算式。框架群的相对粗糙高度与孔隙率共同影响阻力系数大小。透水框架群当量粗糙度、零面位移高度和入侵深度的求解方法需要进一步研究。