函数极限求值的若干方法探究

陈书坤

(山东青年政治学院 信息工程学院，济南 250103)

关于函数极限的求解方法，在高等数学教材中主要介绍了极限的四则运算、两个重要极限、等价无穷小代换、洛必达法则，等等。为了丰富求函数的极限方法，现总结介绍几种高等数学教材中不常用的函数极限求解方法。

1 利用微分中值定理求极限

在利用微分中值定理时需要构造适当的函数，而函数可以通过观察极限的结构来进行合理构造。

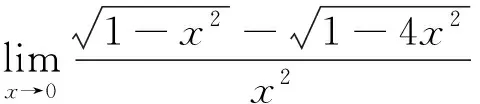
其中ξ∈(1-4x2,1-x2)。当x→0时，ξ=1

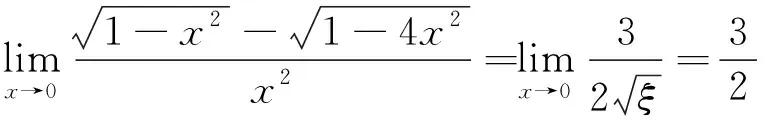
(说明：本题也可用洛必达法则或泰勒展开公式求解。)

2 利用泰勒展开公式求极限

在求解函数极限时有时需要用到泰勒展开公式，尤其是一些初等函数的麦克劳林公式，如ex、sinx、cosx、ln(1+x)、(1+x)α等。在使用泰勒公式时，至于需要将所展函数展开到第几项还需要根据具体情况进行相应处理。例如，若求解的是分式函数的极限，则需要根据分子、分母的幂次来决定，原则是展开后(去掉高阶无穷小)使得分子、分母的最高次幂相等。

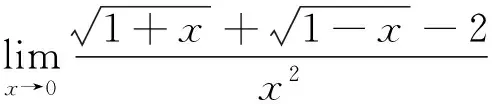
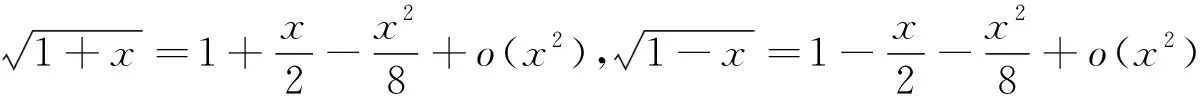
所以原式

(说明：本题也可用洛必达法则求解，但由于本题分子中含有根号，求导时会变得较为繁琐，而使用泰勒展开公式会更简便。)

3 利用积分中值定理求极限

利用积分中值定理可以求某些含有定积分表达式的函数极限。

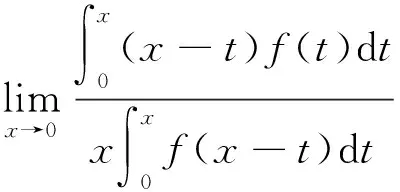
解：由于f(x)在x=0的某邻域内连续，则由积分中值定理可知：

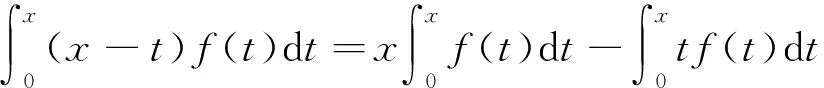
则有：

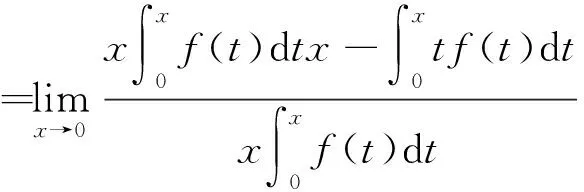
(说明：本题从结构上来看可以使用洛必达法则求解，但在求解时遇到了不符合洛必达法则条件的情况，因此不能使用洛必达法则。)

4 利用导数的定义求极限

当在函数极限出现有关函数导数的相关条件时，可以考虑根据导数的定义表达式进行求解。

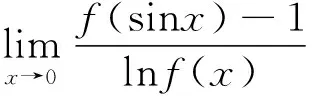
解：由题知

(说明：本题也可以利用洛必达法则和拉格朗日中值定理求解。)

5 利用函数的幂级数展开式求极限

当所求函数极限中出现诸如ex、sinx、cosx、ln(1+x)等类似形式的函数时，可以考虑将其展开为幂级数。该方法可以将复杂函数表示为简单的幂级数，从而便于求出函数极限。

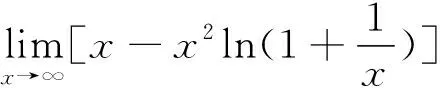
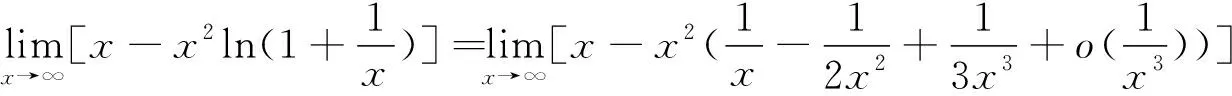
(说明：该题也可以通过换元将其变为分式函数，然后使用洛必达法则求解。)

6 利用函数与极限的关系求极限

有些函数的求极限问题可以根据函数与极限的关系进行求解：若limf(x)=A，当且仅当f(x)=A+α(x)，α(x)→0

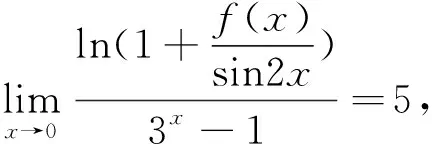
于是f(x)=sin2x·[e(5+α(x))·(3x-1)-1]

而e(5+α(x))·(3x-1)-1～(5+α(x))·(3x-1)(x→0)

则有：

(说明：本题也可以直接根据四则运算法则及等价无穷小代换求解。)