基于自适应变异的多目标鸽群优化的无人机目标搜索
霍梦真段海滨
(1.北京航空航天大学自动化科学与电气工程学院仿生自主飞行系统研究组,北京 100083;2.鹏城实验室,广东深圳 518000)
1 Introduction
The modern search theory was initially proposed to develop efficient search methods to find enemy marine vessels by Koopman[1],Stone[2]and others.Unmanned aerial vehicles (UAVs)are an indispensable tool for search and rescue of critical,time sensitive missions as they have the advantages of zero casualties,highspeed overload,good stealth performance,short operation time,and low life-cycle cost[3–4].Search theory has been applied to many fields with great success,encompassing applications such as search and rescue missions,exploration,mining,medicine,and surveillance[5].
Early search theory focused on the allocation of search effort to areas within the search region while finding optimal search paths on these areas is intuitively with unconstrained searcher motion.If it is not that case,the search problem of finding the optimal paths would become more complicate for searchers.At present,some studies of the search problem as an optimal control problem are conducted in continuous time and space[6],which are generally applied to a very restricted set of initial target distribution.There are many different approaches to solve this problem.Zhang et.al[7]presented a probabilistic path planning method for target search to reduce the expected-time cost in uncertain environments.Tang et.al[8]addressed an improved grouping strategy based on constriction factors particle swarm optimization for multiple targets search in unknown environments.Chen and Chang[9]proposed an agentbased simulation for multi-UAVs coordinative sensing.Sun and Duan[10]presented a restricted-direction target search approach based on coupled routing and optical sensor tasking optimization.To simplify the optimization problem,Qiu and Duan[3]addressed a decoupling receding horizon search approach to agent routing and optical sensor tasking,which was employed in this paper.
In the search problem,a single UAV aims to search for several targets in a bounded planar region.The agent is equipped with a gimbaled optical sensor that can be steered around to view a limited area of the search region[10].The optical sensor will collect information about the environment in the form of automatic target recognition(ATR)data and determine whether the target is located at the specific region or not.The problem mentioned above can be turned into an multi-objective optimization problem(MOP)by selecting the approximate controlling means and mathematical model.
In order to solve MOPs,multi-objective evolutionary algorithms(MOEAs)has been becoming one of the major research topics during recent years.Among the evolutionary algorithms (EAs),pigeon-inspired optimization(PIO)is a novel swarm intelligence algorithm based on the behavior of homing pigeons,invented by Duan and Qiao[11].Due to the high convergence speed and ease of implementation,PIO algorithm has been applied in many fields such as neural network[12],path planning[13],and so on.However,PIO is easy to be trapped into local optimum and uneven distribution while dealing with complex multi-objective problems.Therefore,this paper presents an improved multiobjective pigeon-inspired optimization algorithm based on the adaptive flight mechanism and mutation mechanism.These two mechanisms are designed to reinitialize the pigeons to improve the search capability of the algorithm and prevent pigeons from falling into local optimum and premature convergence.
The remainder of this paper is organized as follows.Section 2 describes the problem formulation,covering the model description,the design of the multi-objective optimization cost function,and the search approach.Section 3 illustrates the improved MOPIO algorithm.Simulation validation,together with comparison against the traditional approach,is presented in Section 4.Section 5 provides conclusions and some possible paths for future work.
2 Search problem
A single UAV is considered to be tasked with exploring an area of interest in order to search multiple targets in a bounded planar region.The UAV is equipped with a gimbaled optical sensor,which can be steered around to view a limited area of the search region.
This section formulates the target search problem as a discrete-time optimization and the approach that controls the UAV and the optical sensor to find the targets as soon as possible.
2.1 UAV dynamics and sensor model
Denote the controlled variables of a UAV at timekby the velocityv(k)and the heading angleθ(k),wherekis a discrete time variable belonging to the nonnegative integers.Without loss of generality,we assume that the UAV keeps the fixed flight height while performing a search task.Thus,the kinematic equation of the search agent can be expressed as the following discrete time point-mass kinematics model:
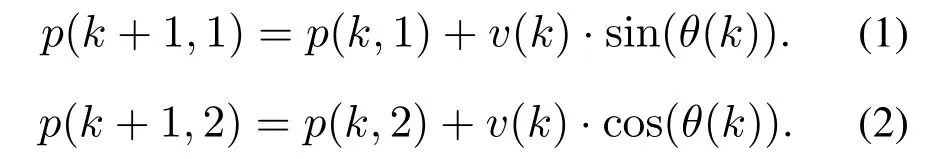
wherep(k+1,1)denotes the horizontal axis in absolute coordinate system of the next current position,p(k+1,2)denotes the vertical axis in absolute coordinate system of the next current position.Due to the maneuverability limitations of the UAV,the velocity has a limited range [vmin,vmax]and the ∆θbetween two consecutive moments is subject to the minimum turning radiusRmin.Velocityv(k)together with the turning radiusRmindescribes the mobility and determines the flight trajectory of the UAV.
During the search process,the region that a sensor can view at a certain moment is called the field of view(FOV),and the subset of the search region viewable by the sensor as it is swept through its entire range of motion is called the sensor’s field of regard(FOR)[10].For each candidate path,the position of UAV can be defined asp(k)=[x(k),y(k)],wherep(k)is the waypoint at timek.As shown in the Fig.1,FOR is considered as the rectangle that takes the current waypointp(k)as center.FOV is set as a square,whose center can move along the centerline of the rectangle.The center of FOV is stated as the sensor taskq(k)that specifies the stare point where the agent will point its optical sensor at timek.Thus,the search problem has been transferred into the problem to obtain the next waypointp(k+1)and the sensor taskq(k).
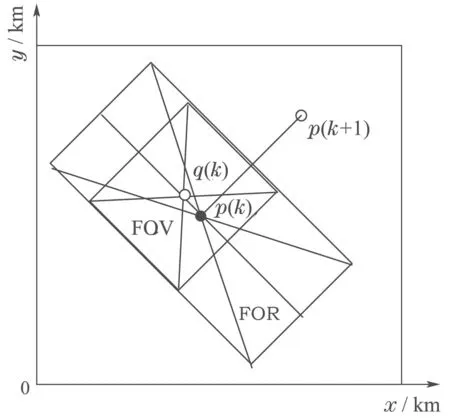
Fig.1 Diagram of the sensor model
2.2 Search map
The graph-based model method is employed to depict the environment information in allusion to searching process.The search region is divided intoM ×Ncells.The coordinate of each two-dimension discrete cell is denoted as (x,y),x ∈{1,2,···,M},y ∈{1,2,···,N}.For the convenience of the following exposition,the cells are numbered by the following equation in a sequence asm ∈{1,2,···,M ×N}:
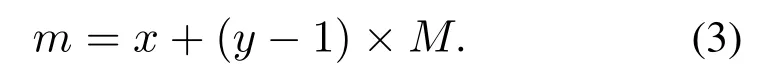
Denote the information structure of each cell asIm(k),including the target occupancy probabilityρm(k)that describes the probability that the search targets exist in themthcell at timekand the environment certaintyχm(k)that describes the certainty of themthcell for the UAV.Im(k)can be stated as follow:

whereρm(k)∈[0,1]andχm(k)∈[0,1].If the target exists in themthcell,ρm(k)=1;On the contrary,ρm(k)=0 while there is no target in themthcell.Similarly,if the UAV fully understands the environment information,χm(k)=1;On the contrary,χm(k)=0 while the UAV knows nothing about the information in the cell.
Consider there existntargets in the search region whose initial positions are unknown.It is reasonable to assume that the position of the target is uniformly distributed.Thus,we can obtain the following equations:
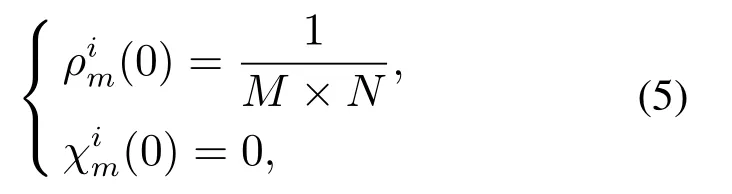
wherem∈{1,2,···,M ×N}andi∈{1,2,···,n}.
During the dynamic search,the search map at timek+1 is updated dynamically based on the state of the agent and the detection results of the sensor at time constantly.The updating principle of theρim(k+1)is stated as follows:
Case 1Theithtarget is detected:
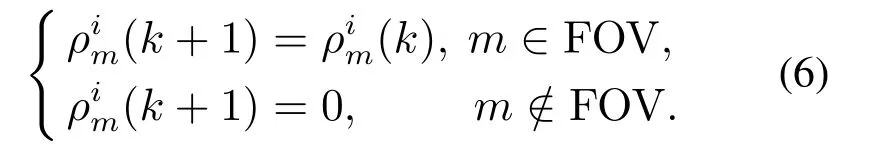
Case 2Theithtarget is not detected:
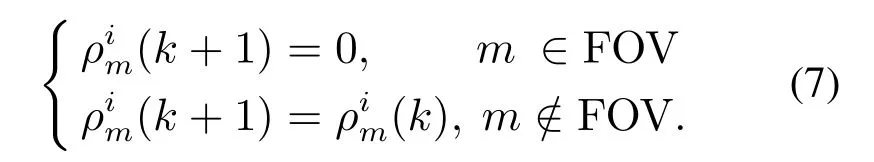
The updating principle of theχim(k+1)is stated as follows:{

2.3 Cost function
The search problem of the UAV is a rather intricate multi-objective optimization problem.It is crucial to select the multi-objective cost functions associated with each candidate path.The introduction of the set of cost functions are shown below:
F1describes the probability of finding target on the candidate path under the action of the controlv(k)andθ(k).
F2describes the entire environment certainty for agent which could be increased by probing the region unknown away from the cells withχm(k)=1.
F3describes the time cost or fuel cost between two continuous waypoints.
F4reflects the behavior of avoiding the threating regions composed of natural threats,missiles threats,and no-fly zone.The value of this function represents the cost to be paid by the drone crossing the threat zone.
F5is designed to estimate whether the trajectory of UAV is within the limited search region.
The better results of search task require larger value of cost functionsF1,F2,F3and lower value of cost functionsF4,F5.Therefore,to unify the optimization,weadopt the inverse value of cost functionsF1,F2andF3.
2.4 Receding horizon control search approach
The receding horizon control (RHC)search approach with the advantage of online processing constraints on control input and output could describe the control problem as a constrained optimization problem of finite time[14].The primary steps of the RHC search controller are as follows:
Step 1Initialize the agent waypointp0at timek,optimize five cost functions based on the search map information and obtain a set of the optimal control variablesv(k)andθ(k)inNsteps;
Step 2Choose the first item of control variables as the agent RHC inputs and abandon the others;
Step 3Reach the next waypointp1at next time(k+1)by the control inputs;
Step 4Obtain the search result by sensor at waypointp1and update the search map information structureIm(k);
Step 5Update the current time and the agent waypoint as initial value,return to Step 1.
The whole process of RHC search approach is illustrated in Fig.2.
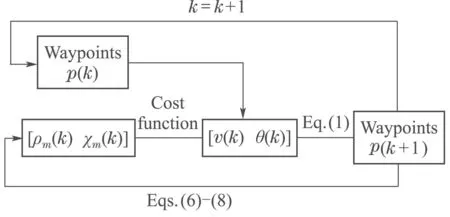
Fig.2 Process of RHC search approach
3 Search problem
Pigeon-inspired optimization is a population-based bio-inspired swarm intelligence optimization algorithm based on the special navigation behavior of the homing pigeons.In this algorithm,two operators(map and compass operator,landmark operator)are employed to guide the pigeons to find the destination.When pigeons start their journey,they may rely more on compass-like tools.While in the middle of their journey,they could switch to using landmarks when they need to reassess their route and make corrections[11].Due to the imperfection of the basic multi-objective pigeon-inspired optimization algorithm[16],two mechanisms are employed to strengthen the capability of global exploration and local exploitation.
3.1 Main algorithm
The basic PIO algorithm adopts two independent useful cycles to mimic the characteristics of the homing pigeons.To improve the efficiency of the optimization process,the two cycles are integrated to one main cycle using two adaptive flight parametersk1andk2.The velocityViand positionXiof each pigeon at timet+1 are updated according to the following equations:
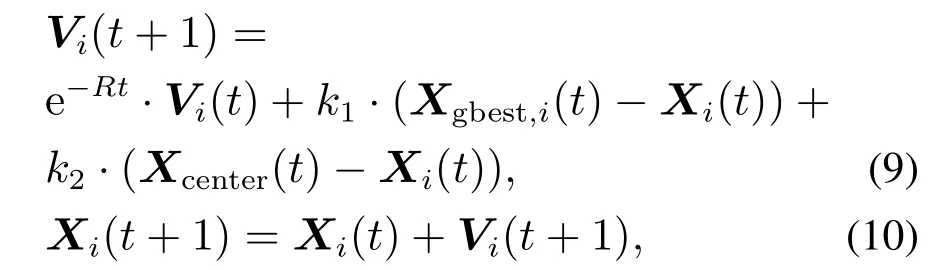
whereRis map and compass factor,tis the time of iteration,iis the number of pigeons in the swarm andi ∈{1,2,···,N},Xgbest,irepresents the best position in the flight path of the pigeon.Xcenteris the center of the pigeon’s position used as the reference direction during the last period of flight.The adaptive flight parameters and center positionXcenterare obtained by the following mechanisms.
3.2 Adaptive flight mechanism
In the flight process of pigeons,the balance of theV(t),Xgbest,andXcenteris crucial to the tradeoff between the exploration and exploitation for the evolutionary properties,such as convergence,diversity,and optimal solution.There exist some challenges on the optimization of the flight parameters.Thus,the adaptive flight mechanism is proposed in this paper to balance the global exploration with local exploitation by utilizing the diversity information and population SP information[17].The calculation of the population SP information of theithpigeon at(t+1)iteration is shown below:
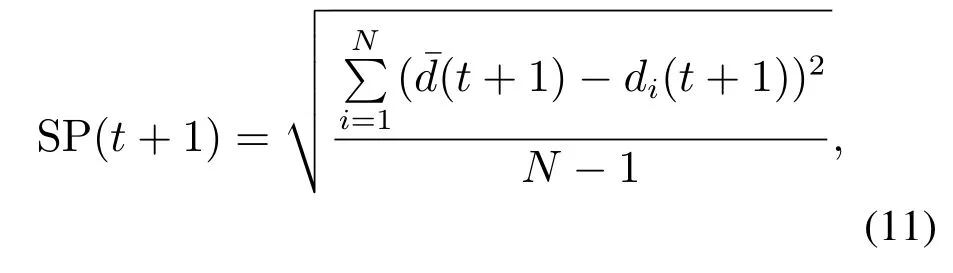
wheredi(t+1)is the minimum Manhattan distance between the position of theithpigeon and other pigeons,d(t+1)represents the average value of thedi(t+1)for all pigeons.During the optimization process,the pigeons are with nonlinear characteristics intricately[15].Thus,a special nonlinear function is proposed to describe this process:
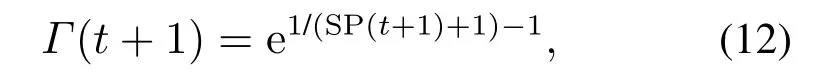
whereΓ(t+1)is the adaptive nonlinear function of the flight process.The initial values of adaptive flight parameters are random numbers created according to the uniform distribution.Considering the value ofΓ(t+1),the adaptive flight parameters are updated as follows:
Case 1SP(t+1)=SP(t):

Case 2SP(t+1)>SP(t):

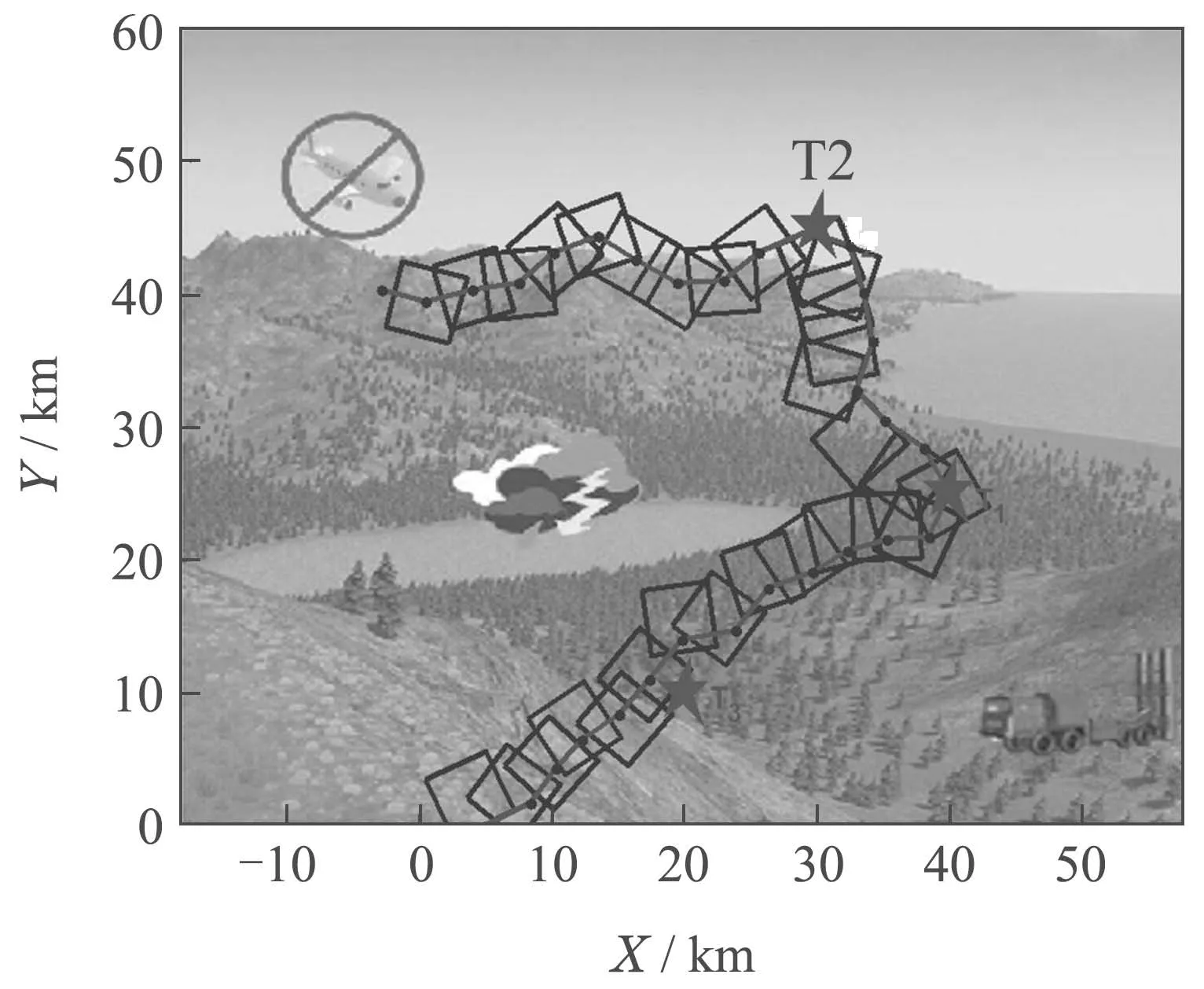
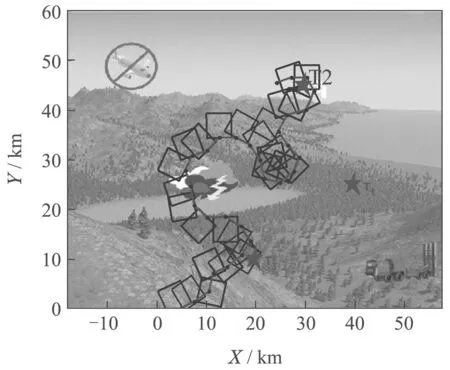
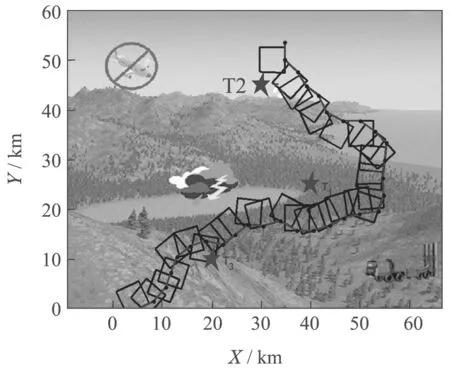
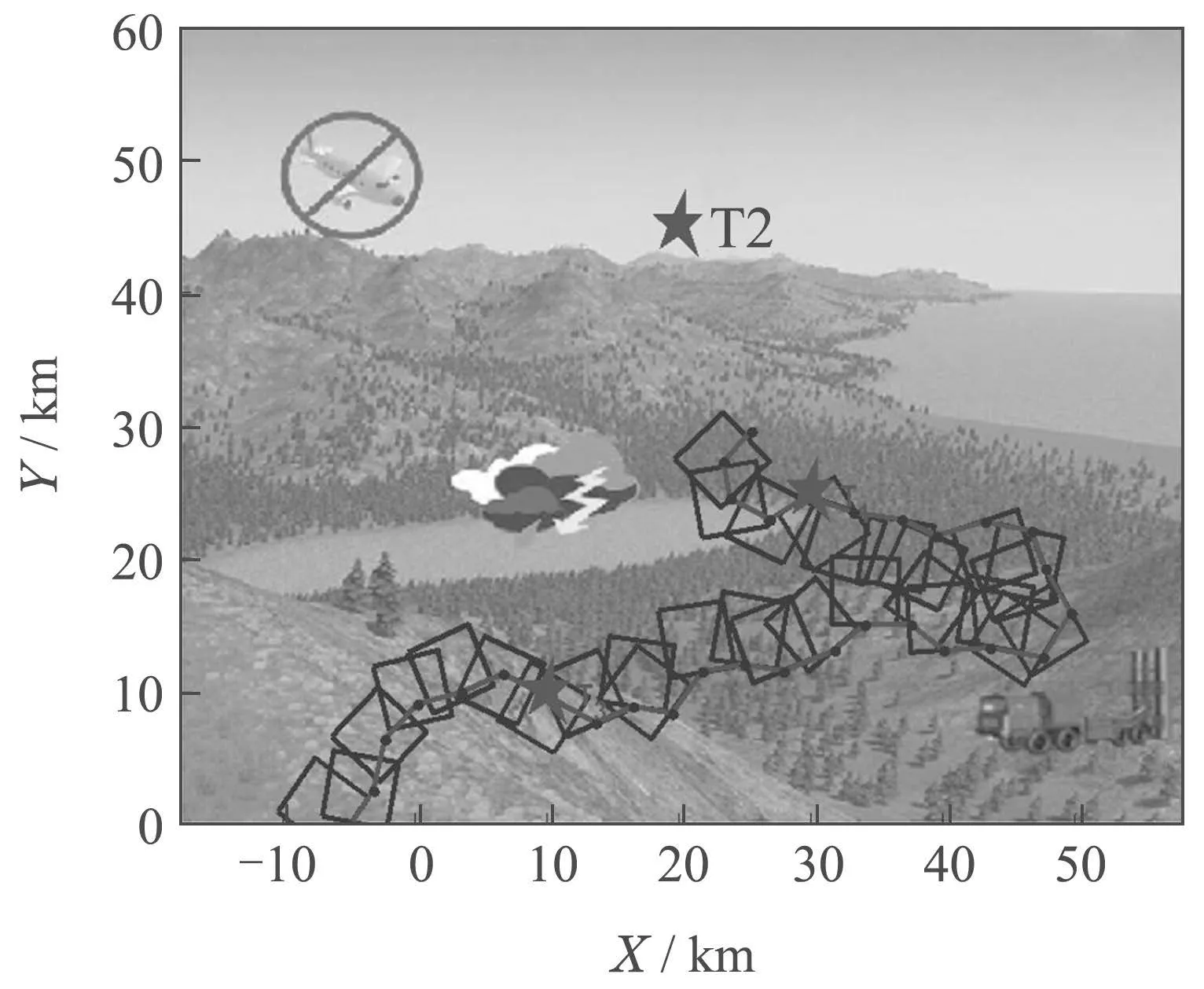
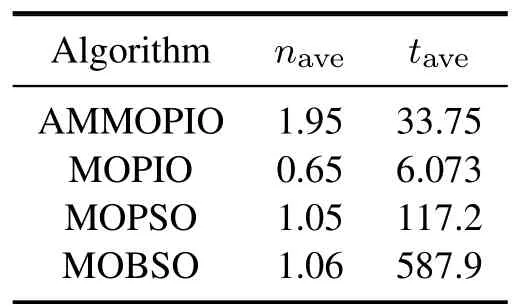
Case 3SP(t+1) The variation of the population SP information reflects the distribution of the pigeon flock.That is to say,the increasing value of SP means the inhomogeneity of the pigeon flock,and the decreasing value of SP means the suitable distribution of the pigeon flock. At the beginning of the optimization,the solutions obtained are far from the true Pareto fronts (PF)with uneven distribution.Based on the above equations,we can see that the parameterk1becomes larger to increase the diversity of the pigeon flock and enhances the exploration ability.During the second half of the optimization,large number of the non-dominated solutions close to the PF are obtained and distributed more evenly.Thus,the parameterk2gets larger to improve the exploitation ability. As the parameterk1increases,the searching process of the optimization mainly depends on theXgbest.While the parameterk2rises,the center positionXcenterplays a major role in the searching process.This demonstrates that the optimization process of the improved MOPIO algorithm corresponds to the navigation mechanism of the pigeon flocks,which illustrates the rationality of the adaptive flight mechanism. The center positionXcenterof the PIO algorithm is calculated by following: The fitness is the function to be optimized: where Case 1 represents the maximization problem,Case 2 represents the minimization problem. Due to the single cost function,there exists the single maximum or minimum value of the function.However,in the multi-objective optimization problems,there exist multiple cost functions.And a single solution which can find the maximum or minimum value for all the objectives at the same time does not exist.Thus,a mutation mechanism is developed to generate the center positionXcenterin the multi-objective optimization problems. Firstly,restore the nondominated solutions in the repository.Then,choose one solutionXrepin the repository randomly and employ the mutation mechanism to improve the chosen solution based on the step mutation operator in Eqs.(19)–(21): wheremis the mutation operator andk=0,1,···,m. The chosen solution is expanded inDdimensions respectively.While the solution with certain dimensionjmutated could obtain the better function value,then thejthdimension ofXcenteris updated.The pseudocode of mutation mechanism is introduced in following steps: Step 1Initialize the flight parameters,population size,repository size,map and compass operator,mutation operator,and maximal iterations. Step 2Initialize the positionX(0)and velocityV(0)of the pigeon flock. Loop. Step 3Calculate the value of cost functions. Step 4Obtain the non-dominated solutions and store the non-dominated solutions in repository. Step 5Select one solutionXreprandomly in repository,use the mutation mechanism Eq.(19). Step 6Calculate the population SP information of the pigeons Eq.(11). Step 7Calculate two flight parameters Eqs.(13)–(15). Step 8Update the position and velocity Eqs.(9)–(10). End loop. The receding horizon control search approach is utilized to solve the search problem and the AMMOPIO algorithm is designed to optimize the parameters of RHC search approach.The holistic search process is depicted in Fig.3. In the simulation,suppose there is a single UAV agent searching for three stationary targets whose positions are unknow in the bounded planar region.The UAV is expected to search the targets as many as possible in the shortest time with multiple goals,consisting of improving the certainty of environment,reducing fuel cost,avoiding the threats,and staying in the task search region. The sampling time is set to be 20 s,and 30 RHC circles are conducted in one simulation.In one single circle,the AMMOPIO algorithm runs 100 times.The parameters and constraints of the simulation are shown in Table 1.The initial states are shown in Table 2.The control parameters of AMMOPIO are given in Table 3. Fig.3 Process of target search Table 1 Optimization parameters and constraints Table 2 Initial states Table 3 Control parameters of AMMOPIO algorithm The performances of the AMMOPIO algorithm are compared with the basic MOPIO algorithm and other two state-of-the-art methods,including multiobjective particle swarm optimization (MOPSO)and multiobjective brain storm optimization (MOBSO).The basic MOPIO algorithms is composed of two cycles and the center positionXcenteris randomly selected in the non-dominated solutions without mutation mechanism.The best results of four algorithms in 20 simulation cycles are illustrated in Figs.4–7. Fig.4 Search results of AMMOPIO algorithm Fig.5 Search results of MOPIO algorithm Fig.6 Search results of MOPSO algorithm Fig.7 Search results of MOBSO algorithm Table 4 Statistic data of four algorithms In Fig.4,three signal represents the threat region,respectively,no-fly zones,bad weather region,and missiles threat.T1–T3 denotes three stationary targets to be found.The red short lines between the adjacent dots are the paths of the UAV.The blue squares are FOV.The average number of the targetsnavefound in 20 simulation cycles is recorded in Table 5 and thetaverepresents the average running time of the simulations. Observed that the agent in Fig.4 found three stationary targets,while successfully avoiding the threats and remaining in the search task region.On the contrary,the results in the Figs.5–7 show that the agent could only find two of the three targets with winding flight path in the simulation.Compared with other three algorithms,the AMMOPIO method gives a good performance in less valid paths. The statistic data in Table 5 illustrates that the search target optimization with AMMOPIO algorithm could find more than double targets compared with the basic MOPIO algorithm although more time is needed.The MOPSO and MOBSO approaches could only find one target approximately in much more simulation time in contrast to the AMMOPIO algorithm.The average number of the targets could reflect the stability of the algorithms.The statistic data shows the feasibility of our proposed algorithm in the practical environment. As we can see in the results above,our proposed AMMOPIO algorithm could find most targets in the finite time.It could be estimated that it could find more targets as there are more than three targets.Therefore,it is clearly that the performance of AMMOPIO algorithm is superior to other three methods.Contrast to the algorithm in[3],this paper employed the multi-objective optimization algorithm to solve the target finding problem.That is to consider all requirements simultaneously rather than scaling down the value of requirements.Even though there is a gap between the number of targets found and the number of targets existing,a preliminary evaluation can be still given that the optimization purposes of searching targets has a basic implementation. This paper presented an AMMOPIO algorithm for the optimization of target search problem.The adaptive flight mechanism could improve the distribution of pigeons with applicable diversity and convergence.The mutation mechanism is used to simplify the model of PIO to improve the search efficiency.From the comparative results in simulation,it can be concluded that our proposed AMMOPIO algorithm does perform superiority in the number of targets found and the time taken to find targets compared with other three approaches.We will also develop more theoretical research on multiobjective optimizations to enhance the ability of unmanned system in the process of performing missions.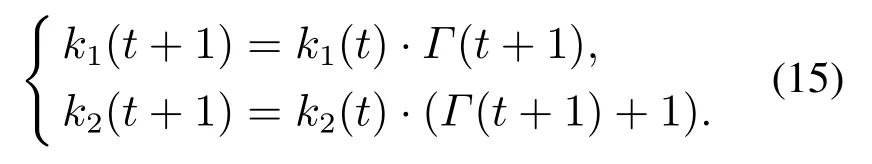
3.3 Mutation mechanism
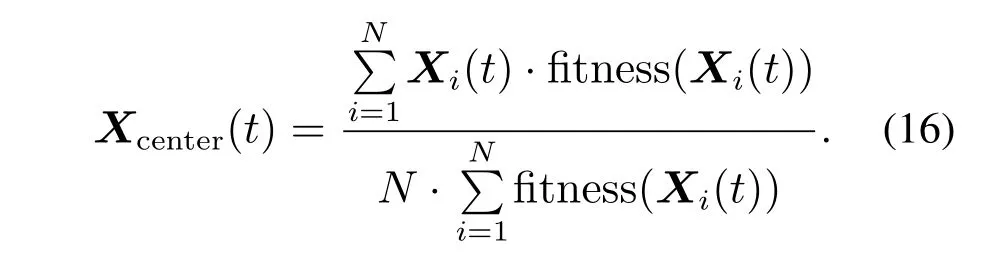
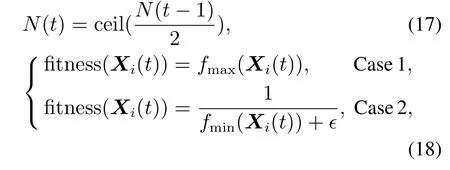
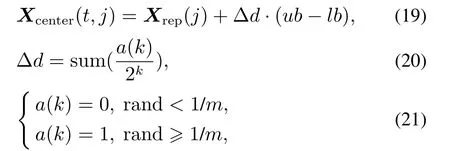
4 Simulation results



5 Conclusion

