支持密钥隔离的属性代理重加密方案

刘 艳，段 茹，琚名扬

1(大连大学 辽宁省北斗高精度位置服务技术工程实验室，辽宁 大连 116622)

2(大连大学 信息工程学院，辽宁 大连 116622)

E-mail ：linda_whb@163.com

1 引 言

随着云计算技术和大数据的飞速发展，云存储方式有效地降低了本地数据存储和管理成本，实现了高质量的应用服务.通过云存储技术，数据通信和共享变得比以往任何时候都更加经济和方便.然而，人们在享受云技术带来的好处的同时，还面临着如何使数据能够安全高效共享的问题.

代理重加密(Proxy Re-encryption，PRE)[1]支持代理者在不知道授权人私钥的情况下，将授权人的密文转换为可被被授权解密的密文，解决了云端数据分享的问题.然而，目前的ABPRE方案虽实现了数据共享，但仍存在一些不足之处，限制了ABPRE的应用.其中一个亟待解决的问题是加密密钥的时间限制安全保护[3].在现有的大多数工作中，重新加密密钥是独立于系统时间段生成的，当用户的访问权限发生变化时，这些时间段易因缺乏前向安全保护而造成密钥泄漏问题，而密钥隔离密码体制[4-8]则是解决该问题的有效方法之一.

即使拥有保证密钥安全的方法，仍需要高效的数据访问模式，如今单一的数据共享已无法适应云环境、可以实现一对多的数据访问的方案急需研究.众多加密算法被提出，其中基于属性的代理冲加密方案[2]可将多个属性加密的明文转换成另一组属性加密的密文，极大大提高了数据分享效率.后来，Liang等人利用密文策略，提出了第一个利用属性实现自中心访问管理的CP-ABPRE[9].为提高计算效率，出现了恒定双线性对的加密方案[10].同时为提高安全性，具有CCA安全性的ABPRE方案和可匿名的代理重加密方案等陆续被提出[3，11，12，16].上述方案虽然使得数据共享变得更加高效快捷，安全性也有提高，但方案中加密密钥是独立于系统时间段生成的，当用户的访问权限发生变化或密钥暴露时，均无法实现前向安全保护[13，14].2017年，Hong等人提出的方案[15]实现了将属性与密钥隔离相结合的方式实现了数据的安全保护，但其采用的与门访问结构并不能很好的适应当前云端的数据访问控制需要.

针对上述存在的问题，本文将密钥隔离技术与基于属性的代理重加密方案相结合，并采用LSSS线性共享矩阵的访问结构，提出一种支持密钥隔离的属性代理重加密方案.方案采用密钥隔离技术将生存期分为离散时间片，用户的私钥定期刷新.当系统进入一个新的时间段时，以前时间段中的重新加密密钥无法在新的时间段中为用户生成有效的密文；同时，在新时间段失去访问权限的用户将无法解密授权用户的密文.方案精简了协助者密钥，在私钥产生和更新过程避免了增加多余的计算量，证明了随机预言模型下的安全性.

2 预备知识

2.1 双线性映射

定义1.设有两个阶为素数p的乘法循环群.g，gT分别为G，GT的生成元，双线性映射e：G×G→GT，同时满足以下性质：

·双线性 ：存在e(ga，gb)=e(g，g)ab，其中∀a，b∈Zp.

·非退化性：存在g∈G，使得e(g，g)≠1.

·可计算性：对∀(u，v)∈G，e(u，v)都能有效的计算.

2.2 判定性q-parallel BDHE问题假设

设有两个阶为素数p的乘法循环群，生成元g∈G，随机选取元素a，s，b1，…，bq∈Zp，给定一个多元组：(g，gs，ga，…，g(aq)，g(q+2)，…，g(a2q))，(gs·bj，ga/bj，…，g(aq/bj)，g(q+2/bj)，…，g(a2q/bj))其中∀1≤j≤q；(gasbk/bj，…，g(aqsbk/bj))其中∀1≤j，k≤q，j≠k.

如果不存在一个多项式时间算法能以一个不可忽略的优势T输出T=e(g，g)aq+1·s∈GT，则称判定性q-parallel BDHE假设成立.

3 方案构建

本文采用的系统模型如图1所示，用户将数据加密后上传至云端后通过代理服务器将转换后的密文CT′发送给被授权人，但因重加密密钥中包含了用户的私钥信息，当服务器与一些被授权人串通时，用户将无法避免自身权益和隐私权受到损害.系统加入了密钥隔离技术，当进入t2时间段时，协助者辅助用户计算出新私钥SK2.假设被授权人已被剥夺访问权限，且代理服务器与被授权人于t1时刻合谋计算出的用户私钥SK1已失效，被授权人将无法得到用户加密后的信息，从而保证了用户的隐私及数据的安全性.

图1 系统模型图

系统中云服务器主要负责存储用户加密后的数据和提供数据重加密服务.数据拥有者即用户，负责将加密自己的数据上传至云端、生成tl时刻的私钥及更新下一时间段私钥.协助者负责进入新的时间段后更新用户私钥组件，帮助用户更新私钥.被授权者想获得用户上传的隐私数据，要取得访问用户的访问权限，如果符合，云服务器将重加密用户的文件，将重加密后的文件发送给被授权人.本系统算法工作流程如图2所示.其中

1)密钥生成：由用户和被授权者生成各自的密钥.

2)密钥协助更新：协助者作为辅助用户更新私钥的部分，负责给用户发送私钥更新组件.

3)私钥更新阶段：用户通过协助者计算的更新组件生成当前tl+1时刻的私钥.

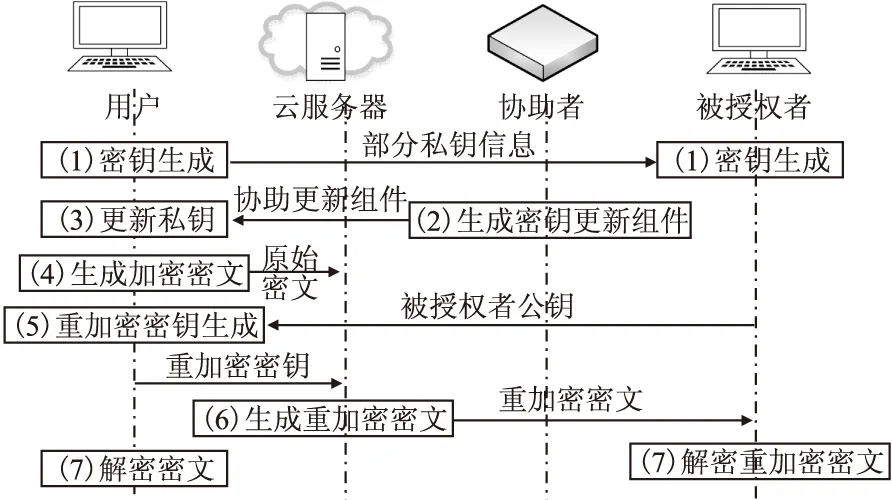
图2 算法工作流程图

4)密文生成阶段：用户使用当前tl+1时刻的私钥加密明文生成原始密文.

5)重加密密钥生成阶段：用户结合被授权者的公钥生成重加密密钥并发送给云服务器.

6)重加密密文生成阶段：云服务器根据重加密密钥执行重加密算法，生成重加密密文并发送给被授权者.

7)解密阶段：用户及被授权人执行解密算法，若符合访问结构，则分可解密原始密文及重加密密文，否则则无法得到明文.

4 算法实现

4.1 方案的具体实现

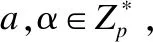
协助密钥更新HkUpdate(MSK，S)：此算法为协助密钥更新组件密钥由密钥协助者执行(密钥协助者可与委托者为同一人).输入主密钥MSK和用户属性集S.当系统进入从tl到tl+1的新周期时，密钥协助者计算具有属性S的密钥刷新组件：tl时刻的密钥协助组件为HSKtl=H1(x，tl)h；tl+1时为HSKtl+1=H1(x，tl+1)h.协助者更新公式为 ：HSKtl→tl+1=HSKtl+1/HSKtl=(H(x，tl+1)/H(x，tl))h.当tl+1到来时，用户为属性集S和被委托者可使用此组件更新密钥.

私钥更新SkRef(HSKtl→tl+1，SK，S)：此算法为私钥更新算法，由用户执行.输入密钥协助更新组件HSKtl→tl+1、用户私钥SK和用户属性集S.当系统进入从tl到tl+1的新周期时，用户计算：

Kx，tl+1=Kx，tl/HSKtl→tl+1=gβH1(x，tl+1)h

计算完成后输出更新后的私钥：

SK={K，L，{Kx，tl+1}∀x∈S}.

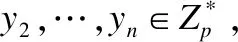
CT={(M，ρ)，A1，A2，A3，Bi，Ci∀i∈[l]}.

最后输出重加密密钥：

RK={rk1，rk2，rk3，rk4，Rx，tl}.

重加密密文生成ReEnc(CT，RK)：算法由半可信代理服务器执行.输入初始密文CT和重加密密钥RK.重加密密钥RK重加密密文CT′的计算过程如下：

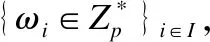
(1)

最后输出重加密密文：

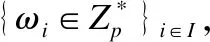
(2)

然后计算A1/Z=m，得到明文消息m.

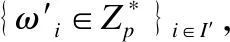
(3)

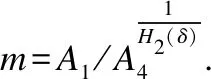
4.2 正确性

1)正确性验证：

=e(gs，gα)

同理可得Z′=e(gs′，gα)，解出密文为：

A1/Z=m·e(g，g)α·s/e(g，g)sα=m.

2)重加密算法中A4的正确性验证：

=e(g，g)sαH2 (δ)

5 安全性证明

5.1 数据机密性

定理1.随机预言模型下，如果q-BDHE困难问题是难解的，那么本方案在是不可区分性安全的.

证明：假设在一个概率多项式时间内，构造敌手A和一个挑战者C，如果敌手A以不可忽略的优势ε攻破本方案随机预言模型下不可区分性的安全游戏，那么可以利用敌手A的输出求解q-BDHE困难问题.输入问题实例y和T，进行如下模拟游戏：

1)初始化：敌手A发送给挑战者C一个想要挑战的访问结构(M*，ρ*)，其中M*为l*×k*，l*，k*≤q的矩阵.

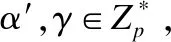
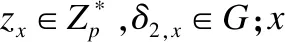
否则挑战者C设置δ2，x=gzx.最后挑战者C返回δ2，x，给敌手A并将元组(x，zx，δ2，x)添加至H1列表中.

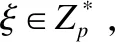
3)阶段1：敌手A发起询问，挑战者C作如下响应：

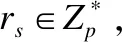
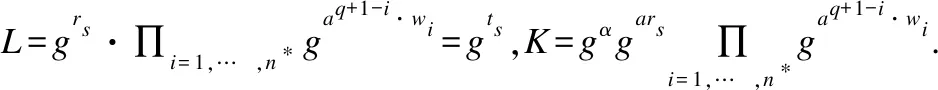
最后，挑战者C将(S，SK)添加到列表中并发送给敌手A.

②协助密钥更新查询OHkUpdate(MSK，S)：敌手A提交查询时间片段tl到tl+1的密钥更新请求，挑战者C计算：HSKtl→tl+1=HSKtl+1/HSKtl=H1(x，tl+1)h/H1(x，tl)h，并将结果返回敌手A.

③私钥更新查询OSkRef(HSKtl→tl+1，SK，S)：挑战者C计算Kx，tl+1=Kx，tl/HSKtl→tl+1=grsH1(x，tl+1)h，将结果返回敌手A.

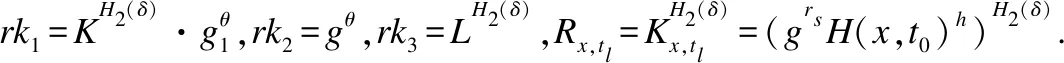
4)挑战：令b∈{0，1}，挑战者C负责加密消息mb，mb为敌手A发送，且m1、m2等长，加密后作如下回答：

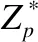
5)阶段2:同阶段1.

6)猜测.设b′敌手A为猜测结果.如果b′=b，挑战者C输出0，说明T是GT的随机值.如果b′≠b则输出1，则有T=e(g，g)aq+1·s，说明敌手A能够以ε的概率得到有效密文：

Pr[b′=b|(y，e(g，g)aq+1·s)=0]=1/2+ε.因此，战者C成功解决决定性q-BDHE问题的概率为ε/2.

5.2 抗合谋攻击性

在本方案中，假设代理服务器将代理重加密密钥发送给被委托者恶意合谋，此时被委托者结合自身私钥可以恢复出δ的值，然后根据rk3和Rx，tl得出gβ和Kx，t0=gβH(x，t0)h的值.但是被委托者无法根据rk2和剩下信息得出θ的值，从而得出K的值，如此便不可能得到用户的全部私钥.由此证明，即使代理服务器与被委托人恶意合谋也无法解密没有访问权限的用户密文，从而实现了抗合谋攻击性.

6 功能与效率分析

本文采用医生查看病例的情况及含75个属性的UCI真实数据集Heart Disease来分析说明文献[16]、文献[15]和本方案算法的功能与效率比较结果.实验将医生A设置为数据所有者即用户，将合作的医生B设置为被授权者.当医生A欲与别的医生合作时，可设置访问条件后加密上传至服务器.如当医生A确定与主治劳动引起心绞痛症状的医生B合作，则可设定访问条件为{典型心绞痛&通过劳累引起}.与医生C合作则可设为{(典型心绞痛&通过劳累引起)∨{有ST-T波异常&运动可诱发心绞痛}}.如此患者通过改变访问结构中的条件即可实现数据有针对的分享.

仿真实验环境为64bit Windows10操作系统、实验代码基于jPBC(java Pairing-Based Cryptography Library)库，方案存储空间开销及运行时间结果将使用MATLAB 2014a进行更直观的对比表示.为仿真真实环境，实验设用户属性个数|S|∈[10，50]，访问条件为访问结构属性个数l，实验结果均为20次模拟运算的平均值.

6.1 性能比较

文献[16]的属性代理重加密方案安全性较高，文献[15]同样支持密钥隔离的属性代理重加密方案，因此将本方案功能与文献[16]和文献[15]进行对比分析，如表1所示.其中|G|和|GT|分别代表群G和GT中元素的长度，|U|表示属性集大小，对比了系统建立和密钥长度的存储代价.

表1 方案性能比较

从表1可以看出，文献[16]与本方案同采用LSSS线性共享矩阵，但文献[16]虽是选择密文安全的属性代理重加密方案，具有很好的安全性，但其并不支持密钥隔离的功能，在用户权限发生变更时，本文方案更具安全性.文献[15]虽然同样支持密钥隔离，但采用的灵活度较低的与门访问结构，从系统建立及密文长度可以看出，该算法需要占用更大的资源.由于加入密钥隔离的参数计算，在密钥生成阶段，本方案与文献[15]占用资源要高于文献[16]，且本文方案略高于文献[15]，但相比于密文的开销，如图3所示，本方案更适用于云计算和实际应用.

6.2 效率比较

本节将从效率方面与文献[16]、文献[15]进行对比，比较结果见表 2.其中E表示G上的一次指数操作指数运算，P是表示双线性对配对运算.由于哈希算法、非生成元群元素上的指数操作计算量较小，故忽略不计两种算法的计算量.

表2 计算开销比较

6.3 计算代价比较

本章主要展示了密文生成时间、重加密时间和解密时间的实验运行结果.如图4、图5和图6所示.由于加密时间与用户属性数量相关而与访问结构匹配属性数量无关，文献[15]的始终进行较大的属性数运算，即属性个数取值始终为数据集总数据量，故而在密文加密阶段，密文生成和解密阶段始终需要更多的运算时间.而在重加密阶段，文献[16]随着匹配属性的增加，运算时间直/线上升，本方案却始终保持着最低的时间消耗.结合三个阶段的时间对比可知，本方案在时间消耗方面更具优势.

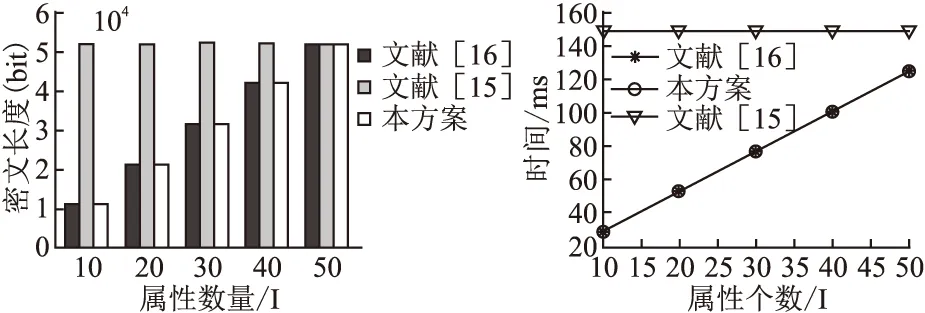
图3 密文存储代价

Fig.3 Ciphertext storage cost

图4 密文生成时间

Fig.4 Time of encryption time

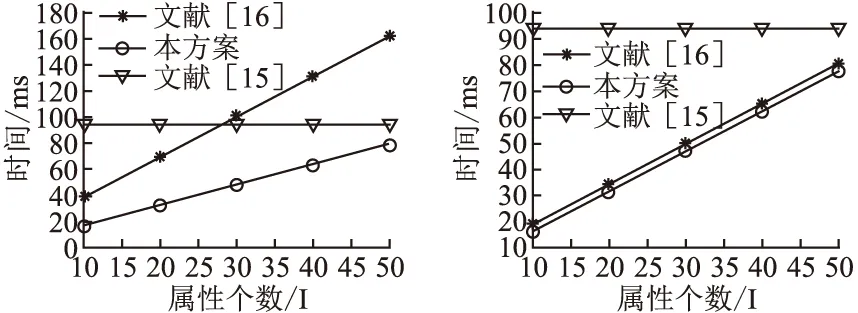
图5 重加密时间

Fig.5 Time of Re-cryption

图6 解密时间

Fig.6 Time of decryption

7 结束语

本文提出了一种支持密钥隔离的属性代理重加密方案，在属性代理重加密方案中加入时间参数，避免了不可信第三方与被授权用户的非法勾结，解决了属性代理重加密方案的秘钥泄露问题.系统生存期被划分为离散的时间片，当系统进入新的时间片时，每个用户都可以进行密钥刷新来限定访问时间，进入新的时间周期后，已经失去访问权限的用户无法对系统中的数据造成威胁，本方案的保密性和抗合谋攻击性已通过安全性证明.此外，相对于已有的支持密钥隔离的重加密方案，功能和效率分析结果表明本案在提高安全性的同时没增加计算开销，且拥有更加灵活的访问策略和计算效率，是一种比较适合当前云环境的加密方案.