高速冲压生产线上下料冗余机械臂的运动学分析
王凯强 ,于鲁川 ,张建华 ,张志刚
(1.山东大学 机械工程学院,山东 济南 250061;2.高效洁净机械制造教育部重点实验室/国家级机械基础实验教学示范中心,山东 济南 250061;3.济南二机床集团有限公司,山东 济南 250022)
汽车产业的竞争日益激烈,汽车部件的生产效率对提高市场占有率具有十分重要的作用,而汽车车身超过60%的外覆盖件部件是通过冲压工艺生产制造,并且上下料系统是冲压生产线最主要的单元,因此,提高上下料机械臂的运动节拍会极大提高汽车覆盖件的生产效率。
通过机械臂在各个压机之间进行物料输送是目前应用最广泛的上下料方式。上下料机械臂轨迹运动规划的优劣直接决定着机械臂的运动节拍、工作效率、关节扭矩、整线配合等性能。将上下料机械臂设计成具有一定的冗余自由度可以提高其运行的灵活性,这种机械臂适合在高度受限的空间中工作,在运行平稳性、使用可靠性等方面要明显优于冗余度低的机械臂[1]。高冗余机械臂可以处理一些非常规功能,但是运动学逆解求解困难,容易出现多解的情况,很多学者在求冗余机械的逆解方法上提供了有效的方法,Samer Yahya等人提出一种几何方法,该方法能够在无限解中运用较少的计算量来得出冗余或者超冗余机械臂的最佳解,这种方法适应性较强,可以适合所有的任意平面n序列机械臂[2]。García-Sedano等人[3]提出一种改进遗传算法将机械臂的运行轨迹进行优化,生成无碰撞的有效的运行轨迹,最大程度的缩短运行周期的时间,此种方法考虑到了机械臂特定组件的几何形状,来调整路径以优化给定冲压单元中的循环时间。在轨迹规划过程中还可以用五次均匀B样条曲线对关键点进行拟合,并采用改进遗传算法对拟合后的曲线进行寻优,然后求得曲线的速度、加速度曲线,通过此方法可以使运行轨迹更加平滑[4]。本文从建立机械臂的正运动学模型出发,对末端执行器轨迹和冗余自由度关节进行规划,进而求出各关节的逆解,旨在对冗余机械臂的求逆解方法提供参考。
1 正运动学分析
1.1 模型分析
图1为冲压生产线上下料机械臂的三维模型,图2为其结构简图,该机构共7个构件,8个低副,可以得出该送料臂的自由度为5,由于其运动全部是在一个平面中运行,所以此机械臂具有两个冗余的自由度。
1.2 正运动学求解
图2中各符号表示的意义为:S为参考坐标系,T为工具坐标系。d0表示各关节角度为0时,滑块D1理论最低点和参考坐标系S原点的距离,d10表滑块D1初始位置和D1理论最低点之间的距离,d1为滑块D1的位移,r2为连杆 R2的长度,r31表示滑块D7的关节点和大摆臂与R2连点之间的距离,d40为滑块D4初始位置距离滑块D7之间的距离,d4为滑块D4的位移,r5为送料臂R5的长度,R6为末端执行器。

图1 送料臂三维模型
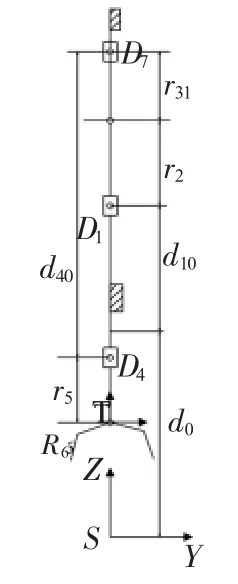
图2 送料臂简图
根据对上下料机械臂的结构分析可知:滑块D7属于从动件,其运动轨迹可根据其他关节的轨迹确定,在进行运行学求解时不需要对其求解。旋量理论在正运动学建模中相对于D-H法具有简洁、几何关系明显的优点,只需要建立参考坐标系S和工具坐标系T,不需要在各关节轴上建立局部坐标系,计算过程也比较简单。
应用旋量理论将参考坐标系S的原点建立在地面和机械臂中轴线的交点,工具坐标系T建立在末端执行器R6的旋转关节处,当上下料机械臂各个关节角为0时参考坐标系和工具坐标系的坐标转换关系为:
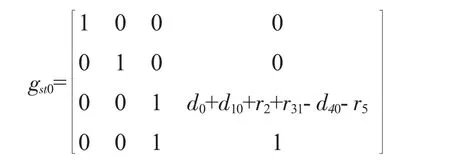
通过分析机械臂的结构可知所有的旋转运动只绕着旋转轴线的转动而没有沿轴线的移动,其节距为0,各关节轴线的单位矢量分别为:
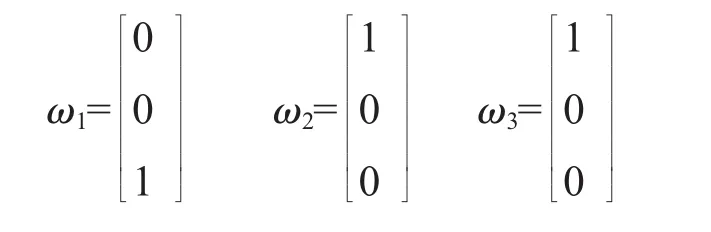

各旋转关节轴线在各关节角为0时经过的点分为:
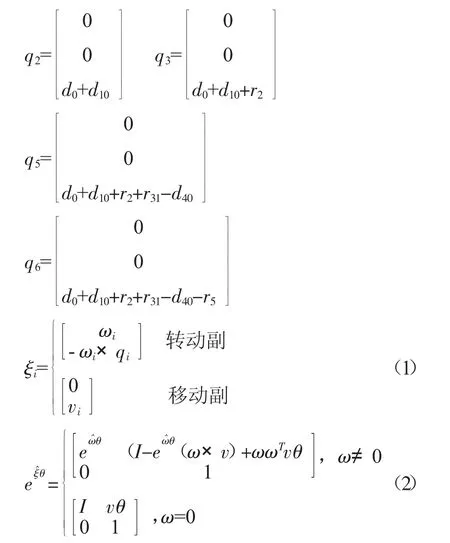
根据旋量理论,关节的运动副旋量计算公式(1)和指数积公式(2)可以得出各关节的指数积公式为:

θ3的初始位姿为180°,其角度变化要添加一个相位角,所以其角度为(π+θ3)。

机械臂的正运动学方程可以通过各关节的指数积矩阵相乘得到:

在正运动学方程中,角度和位移都为矢量,在进行指数积方程运算时不需要考虑其正负,在求解时若符号为正则旋转轴的运动方向表示为在右手坐标系中,沿轴线方向观察为顺时针方向,对于移动轴移动方向为沿Z轴正方向运。其各简化符号的意义为:
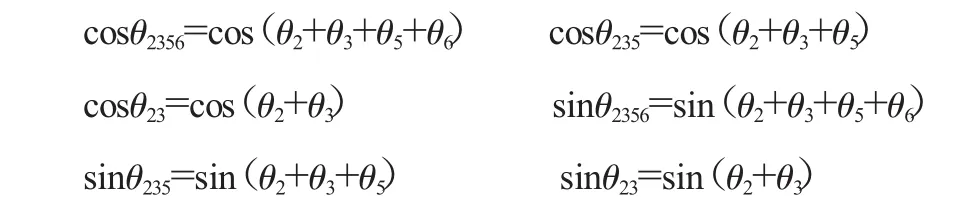
2 逆运动学求解
2.1 末端执行器轨迹规划
在机械臂的轨迹规划过程中,连接起点和终点位姿的具有时间序列的点或者曲线叫做轨迹,用多项式或者样条曲线对曲线关键点进行拟合称为轨迹规划[5,6],用算法将规划后的轨迹进行优化叫做轨迹优化[7]。
在进行末端执行器轨迹进行规划前,需要对其关键点进行设定。送料机械臂末端执行器的运行参数如表1所示,关键点主要设置在Home点和模区边界、取放料点。关键点的选取将直接决定末端执行器运行时的速度、加速度、冲击、关节扭矩等。而其非关键点的位置可以在一定范围内波动,这就能够提供一定的优化空间。
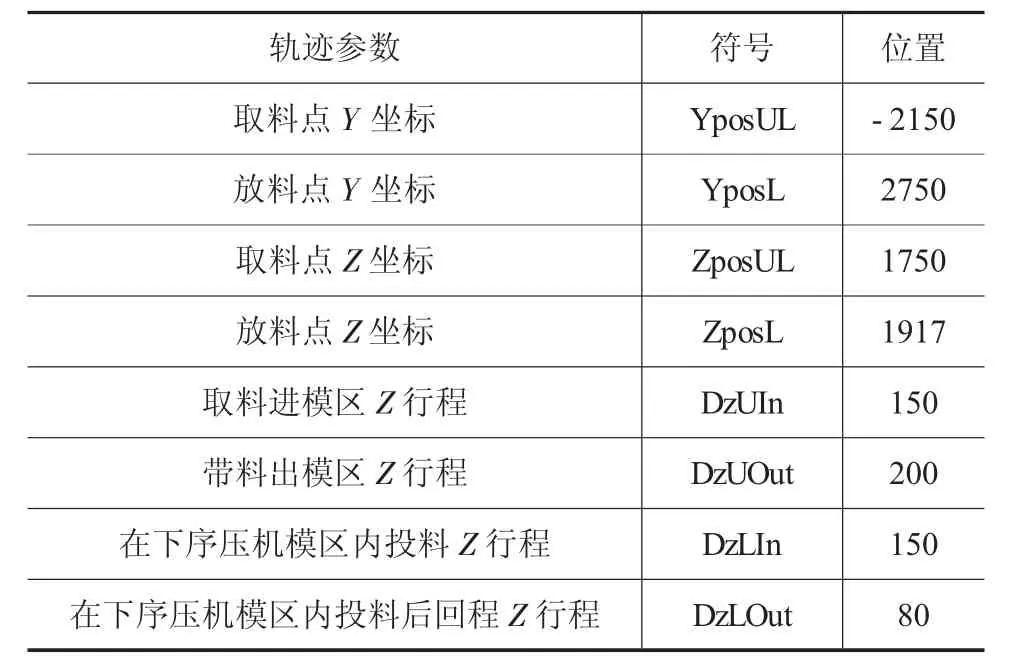
表1 机械臂末端执行器运行参数
B样条是一种以“逼近”为原理的拟合曲线[8],根据表1中末端执行器Y方向和Z方向的运行参数可以对其进行初步的规划,通过在MATLAB中设定关键点采用五次B样条曲线的插值方式形成初步的位移曲线,这样可以保证拟合后的轨迹曲线的位移、速度、加速度都连续可导,使运行轨迹尽可能的平滑。在机械臂初始运行时选取几个点为静点,这样可以避免运行过程中出现加速度突变或加速度无限大的情况。
冲击率的定义为加速度相对于时间的变化率,称之为加加速度[9]。为保证采用五次B样条差值的位移曲线的冲击率尽可能的小,可采用算法对其进行优化,使轨迹更加平滑。遗传算法作为一种通用的智能算法,可以将目标函数进行迭代寻优,最终得到最优解。以加加速度的最大值为优化目标,通过调节非关键点处对应的时间使其最大值尽量减少,经过编码、计算适应度值、选择、交叉、变异的操作,迭代次数设定为50代,最终得出冲击率最小的一条曲线。末端执行器Y方向和Z方向运行轨迹的位移、速度、加速度优化前和优化后的图像如图3、图4所示,加加速度优化前和优化后的图像如图5、图6所示。
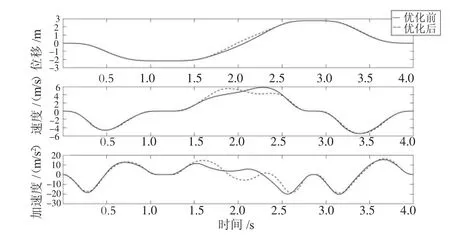
图3 末端执行器Y方向位移、速度、加速度优化前和优化后对比
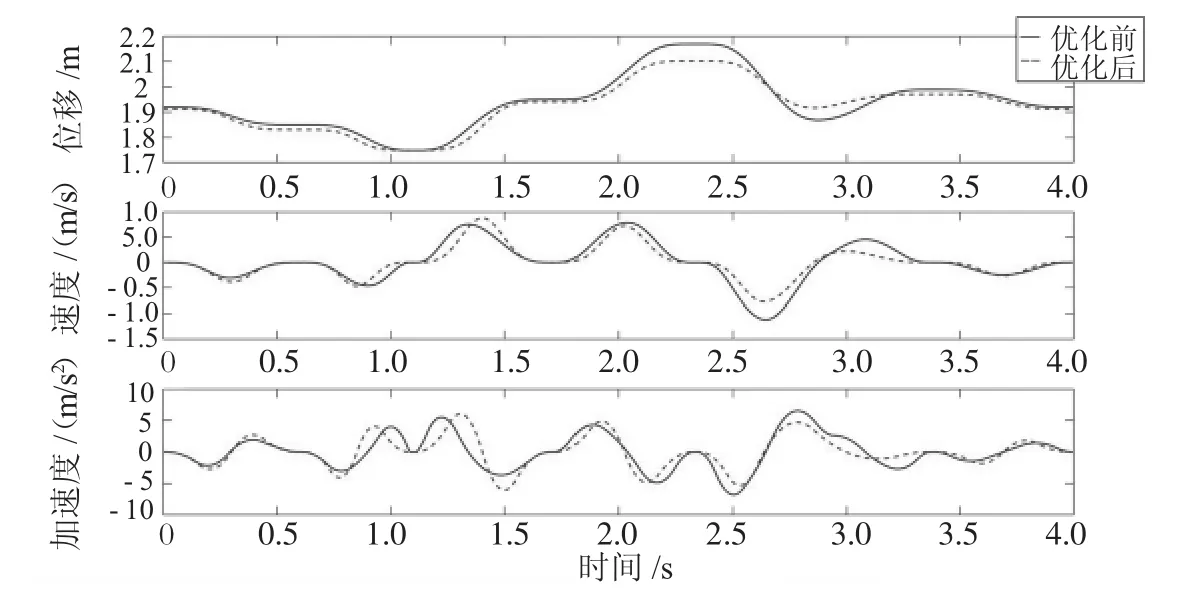
图4 末端执行器Z方向位移、速度、加速度优化前和优化后对比
从图3和图4可以看出,加加速度的调整导致了位移曲线的变化,使运行轨迹在某些非关键点处发生了变化。从图5和图6中可以看出:末端执行器Y方向和Z方向轨迹的加加速度波动范围变小,在绝对值最大处经过优化后明显降低,表明遗传算法的优化效果使冲击率变化更加稳定。
在Matlab中进行优化的过程中,记录每代种群二次加速度的最大值,加加速度的最大值随迭代次数的变化趋势如图7和图8所示。
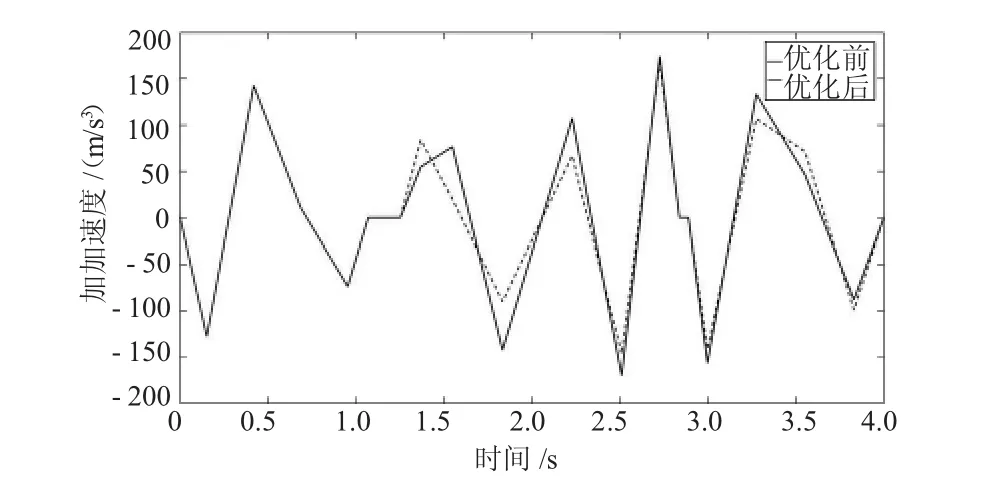
图5 末端执行器Y方向加加速度优化前和优化后对比

图6 末端执行器Z方向加加速度优化前和优化后对比
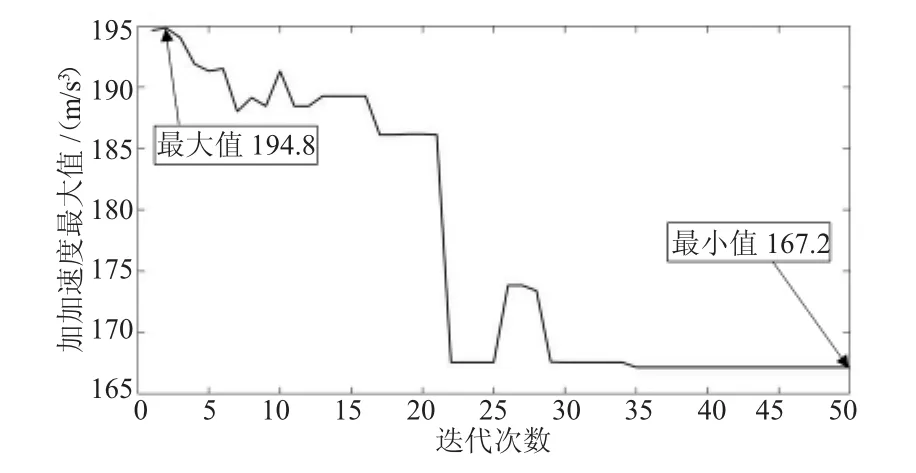
图7 末端执行器Y方向加加速度最大值变化趋势

图8 末端执行器Z轴加加速度最大值变化趋势
从图7和图8中可以看出,Y方向和Z方向加加速度的最大值随着迭代次数的增加呈减小趋势,分别在第35代和40代左右达到稳定状态,加加速度最大值分别减小了14.2%和11.0%,说明遗传算法没有提前收敛且优化效果比较明显。
2.2 冗余关节的轨迹规划
前面提到此送料机械臂的自由度为5,有两个冗余自由度,如果直接求运动学逆解,会导致多解或者无解的情况发生。采用消除冗余自由度的方法可以解决这一问题。在选择消除的冗余自由度时,各个关节都可以作为对象,各关节的求解效率会根据选择消除自由度的关节的不同差别很大。经过多次测试发现对滑块D4和R5_R6关节进行规划,可以大大提高其他关节的求解效率。在对滑块D4和R5_R6关节进行规划时采用的方法和末端执行器的方法一样,固定关键位置点然后采用五次B样条曲线进行拟合,拟合后的运动曲线如图9和图10所示。
2.3 其他关节求解
根据正运动学方程和机械臂的几何关系可得:
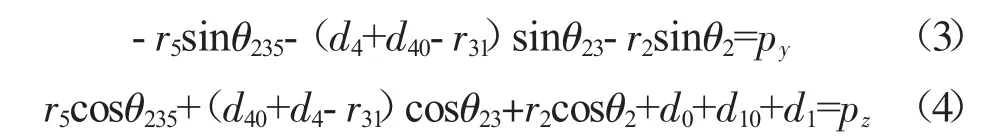

根据 θ2,θ3,r2,r31之间的三角几何关系,并根据正弦定理可得:


图9 滑块D1位移、速度、加速度、加加速度曲线

图10 R5_R6关节位移、速度、加速度、加加速度曲线
式(3)、(4)、(5)、(6)中 py,pz,d4,θ6已经通过轨迹规划求出,四个方程四个未知量,可以求出唯一的解。利用MATLAB的数值计算功能对其他关节进行求解,求解结果如图11~图14所示。
通过图11~图14可以看出求出的其他关节解的运动曲线是连续并且比较平滑,各关节运动过程比较平稳,没有较大的波动,说明前面的轨迹规划和优化效果比较明显。
3 结论

图11 移动滑块D1位移曲线

图12 转动关节D1_R2角度曲线
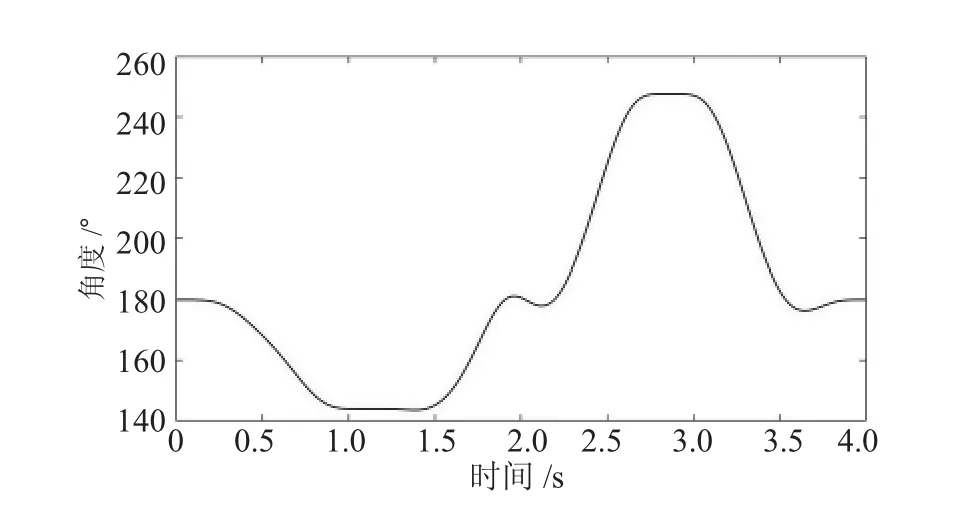
图13 转动关节R2_R31角度曲线

图14 转动关节D4_R5角度曲线
轨迹规划在冲压生产线的上下料系统中发挥着至关重要的作用,本文根据上下料机械臂的工作过程和冗余机械臂特点提出一种通用的运动学分析方法,主要工作有以下两点:
(1)采用五次B样条曲线结合遗传算法对末端执行器的运行轨迹进行规划和优化,使运行轨迹更加平滑,能够将最大冲击率降低10%以上,从而可提高上下料机械臂的平稳性。
(2)针对冗余机械臂的求逆解特点,选择首先对滑块D1和R5_R6关节的轨迹进行规划,提高其他关节的求解效率。

