能量收集和能量协作菱形信道的功率分配策略
孙 莉,李陶深,王 哲
1(广西大学 计算机与电子信息学院,南宁 530004)
2(广西大学 电气工程学院,南宁 530004)
E-mail:1160742044@qq.com
1 引 言
无线通信网络的性能在受到设备电池寿命限制,电池的手动更换或充电导致无线设备的频繁中断.能量收集技术可以从周围环境中源源不断地收集能量,并将这些能量运用在无线通信系统中,大大延长了无线设备的生命寿命,降低维护成本,提高无线网络系统的性能[1-3].然而在能量收集网络系统中,由于能量的间歇性,一些节点的能量可能被消耗殆尽,因此需要指定合理的数据传输和能量管理策略.因此,能量收集无线网络中功率分配和能量转移问题的研究就显得尤为重要.
本文的主要贡献如下:
以最大化系统的端到端吞吐量为目标,提出了一种功率分配和能量转移策略,基于传输节点的能量和数据因果关系约束,构建系统吞吐量优化模型,并将原问题分解为功率分配和逐个时隙的能量转移问题,将两个子问题的解,近似为原问题的最优解.
2 相关工作
近年来,能量收集无线网络中功率分配问题得到了广泛的研究.文献[4]提出了一种配备无限容量电池的能量收集网络节点传输时间最小化方案,通过考虑单用户能量收集无线通信系统中的最优分组调度问题,求得最优离线调度策略.文献[5]利用配备有限电池容量的能量收集传输节点在无线衰减信道中通信,以优化点对点的数据传输,通过控制受能量存储容量和因果关系限制的传输功率时间顺序,来优化在截止时间前的吞吐量最大化问题,给出了最优离线和在线策略.文献[6-10]分别将吞吐量最大化问题及其解决方法的研究扩展到多终端模型,如广播、多址、两跳、干扰和菱形信道,从这些研究中得出了最优的功率分配算法.
能量收集网络是具有间歇可用性网络,网络节点间的能量协作能够提高网络的性能,引起了人们的关注和研究.文献[11]研究了能量收集无线节点的能量转移,并考虑了几种具有能量收集和无线能量转移的多用户网络结构,制定了相应的管理策略.文献[12-14]分别针对单向能量协作的双向、两跳、多址等情况,提出了最优联合离线能量管理策略来获得端到端的吞吐量最大化.文献[15]针对具有能量收集的多终端网络,在吞吐量最大化约束下,提出了一种延迟策略,即能量只有在立即被使用的情况下才进行转移,且转移的能量在当前时隙结束前必须全部使用.该延迟策略的目的是将所述的联合优化问题分解为能量转移和功率分配问题,从而求解最优的传输功率和能量转移策略.文献[16]使用等效的能量转移效率表示法,证明了在最优策略中,节点不能同时发送和接收能量.文献[17]研究了在多终端用户电池能量有限约束下的能量分配问题,将原电池无限容量的假设具体到最佳电池容量并制定出相应策略.
由于地理位置或时间的影响,能量收集网络中能量收集节点收集的能量存在较大的差异.单向能量转移虽然在一定程度上提高了系统端到端吞吐量,但是也存在一些问题.例如对于收集能量较少的节点来说,在不同的时间收集到的能量可能有所不同,此时可以通过双向能量协作的方式实现节点间能量的相互转移和补给.
本文将文献[10]和文献[14]中提出的能量收集的高斯菱形信道模型扩展为双向能量协作的菱形通信网络,提出一种实现端到端吞吐量最大化的功率分配和能量转移策略,通过构建系统吞吐量优化模型,通过分解的方法求得原问题最优解.结果表明,与基于无能量协作和基于单向能量协作的功率分配策略相比,当源节点和中继节点能量收集相差较大时,本文的功率分配策略显著提高了系统的吞吐量.
3 系统模型
本文研究基于能量收集和双向能量协作的菱形信道.如图1所示,包含了一个源节点S、两个中继节点R1和R2,以及一个目的节点D.源节点和中继节点均从环境中收集能量,收集到的能量被存储到相应的电池中.假设源节点和中继节点所配备的电池容量为无限大,目的节点则由固定电源供电.菱形信道的物理层是由广播信道和多址信道串联而成,通过构建无线供电通信网络(Wireless Powered Communication Network,WPCN)为具有不同物理条件和服务需求的多个通信设备供电.本文研究的菱形信道是高斯型菱形信道,即前一部分的广播信道和后一部分的多址信道均为高斯信道,信道噪声为加性高斯白噪声.系统以时隙作为最小传输时间单位,一个传输周期共包含L个等长的时隙.本文所述策略可以扩展到任意时隙长度.
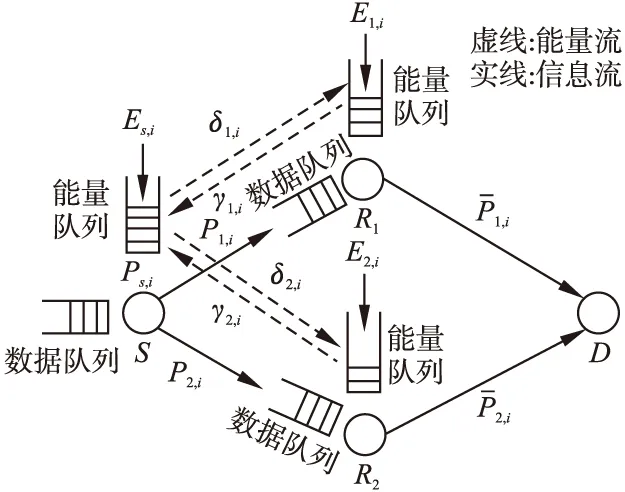
图1 具有能量收集和双向能量协作的菱形信道

在本文的研究中,传输节点S、R1、R2须满足能量的因果约束关系,即在前n个时隙未到达的能量不能使用.因果约束关系如下:
(1)
(2)
中继节点R1、R2还应满足数据的因果关系约束,在前n个时隙未达到的数据不能转发.即:
(3)
系统中端到端的最大吞吐量可以表示为:
(4)
4 功率分配和能量转移策略
当根据能量收集菱形信道最大吞吐量由速率表示时,式(4)中的问题是凸优化问题,然而由于式(3)中的数据因果关系约束,使得问题难以处理.为了简化问题,我们通过对中继施加严格的延迟约束[18].相当于删除中继节点的数据缓冲区,并强制中继节点在同一时隙解码并转发接收的数据.由于中继节点没有数据缓冲区,因此两个中继节点在任何时隙中都不存在未转发的数据,对所有n,式(3)应该满足相等性.因此有:

(5)
(6)
当根据能量收集菱形信道最大吞吐量由速率r1、r2表示时,式(4)中的问题是凸优化问题的证明.
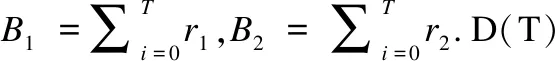
(7)
这里我们只需要证明D(T)是一个凸函数,就可以得到式(4)用速率表示时是一个凸函数,式(4)的问题是凸优化问题.






证明:首先证明两节点间在同一时隙中不能双向能量转移,即δk,iγk,i=0.假设δk,iγk,i≠0,若δk,i≥γk,i>0,则可以用δk,i-γk,i和0分别来代替原来的δk,i和γk,i,(δk,i-γk,i)*0=0.若γk,i>δk,i>0,则可以用γk,i-δk,i0分别来代替原来的γk,i和δk,i,(γk,i-δk,i)*0=0,经过转换后并不会降低最大和吞吐量,由此可证δk,iγk,i=0成立,即两节点间在同一时隙中不能双向转移成立.


证明完毕.


(8a)
(8b)
(8c)
(8d)
(δ1、δ2、γ1、γ2)≥0
(8e)
(8)
其中,{δ1,i、δ2,i、γ1,i、γ2,i的能量约束是式(8c)、式(8d)和式(8e),因此可以定义:

(9)
原问题等价于:
(10)
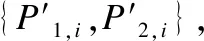
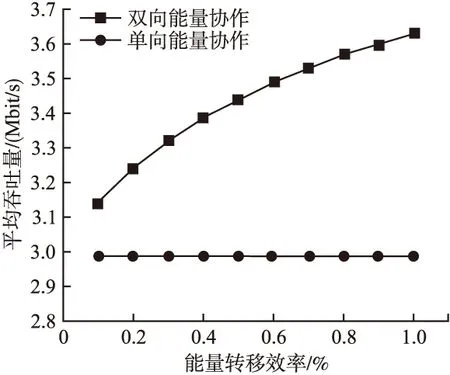
如图2所示,无能量转移的最优功率分配可通过定向注水算法得到.下面对等价能量协作最优功率协作进行简单说明.假设图2中的每个图中L1、L2代表两个时间段,注意到如果有E单位的水(能量)注入到底为L的矩形中,那么注水级就是E/L,定向注水算法的关键部分是可向右渗透的阀门,它只允许水(能量)自从左向右转移.Emax表示电池的最大容量,Ei表示第i时隙中收集到的能量,假设Emax足够大时考虑两时隙L1、L2.如果E0/L1>E1/L2,为了使两个区间的注水级相等,那么就有一些能量从时隙1流向时隙2,该情况如图2(a)所示.然而,如果E0/L1 图2 两时间段情况下带有右透水水龙头的定向注水算法 定理2的证明可参考文献[10]. 证明: 证明完毕. 实验是在Matlab仿真环境下完成的.实验环境设置在1台PC机上,操作系统是Windows 10,CPU为Pentium4 3.0GHz,运行内存8G.运行环境为VSCode,Matlab版本R2018b_win64.实验数据以实际的风电数据为例,由于风能较太阳能在数据上而言具有更大的不确定性,作为模型的输入更能测试模型的顽健性.因此在验证仿真实验中模型的输入数据采用某电网公司2017年7月1日-30日共30天的风功率实际值.实验目的是验证与基于无能量协作和基于单向能量协作的功率分配策略相比,本文的功率分配策略显著提高了系统的吞吐量. 图3给出了T=4,7,10s时菱形信道端到端的吞吐量,纵坐标B1表示源节点通过中继节点R1到目的节点的吞吐量,横坐标B2表示源节点通中继节点R2到目的节点的吞吐量.从图3中可以看出对于每个时间T,端到端的吞吐量是凸的,所以一定存在端到端吞吐量的最大值.随着时间T的增加,端到端的最大吞吐量递增. 图3 系统在不同固定时间的最大吞吐量 图4给出了在能量转移效率α=0.5时,随着时间的变化,两种策略的端到端吞吐量的变化曲线.从图4可以看出,在给定的功率分配和能量转移的策略下,本文策略的端到端的吞吐量优于基于单向能量协作的菱形信道的功率分配和能量转移策略.随着时间的增加,基于单向能量协作和双向能量协作的功率分配和能量转移策略端到端的吞吐量明显都增加. 图4 系统在不同时间段的最大吞吐量 图5给出了随着节点之间能量转移效率变化,两种策略的端到端吞吐量的变化曲线.从图5可以看出,在给定的功率分配和能量转移的策略下,本文策略的端到端的吞吐量优于基于单向能量协作的菱形信道的功率分配和能量转移策略.随着能量转移效率的增大,基于单向能量协作的功率分配和能量转移策略端到端的吞吐量保持不变,而基于双向能量协作的功率分配和能量转移策略端到端的吞吐量明显增加.这是因为源节点和中继节点收集的能量相差较小,所以没有从源节点到中继节点节点能量的转移. 图5 不同能量转移效率下2个策略的系统吞吐量比较 图6给出的是3个策略端到端吞吐量随着源节点Es的收集能量最大值变化的曲线.实验中假设α=0.5.从图6可以看出,在源节点收集能量较少时,基于单向能量协作和无能量协作信道的功率分配和能量转移策略的吞吐量性能接近,本文策略的吞吐量高于基于单向能量协作和无能量协作的功率分配和能量转移策略.随着源节点收集能量最大值的逐渐增大,基于单向能量协作、双向能量协作的功率分配和能量转移策略的吞吐量性能差距逐渐变小,但是本文策略的吞吐量性能依然优于基于单向能量协作和无能量协作功率分配和能量转移策略. 图6 不同源节点收集能量最大值下3个策略的系统吞吐量比较 本文基于能量收集和能量协作的菱形信道,提出一种能够实现系统端到端的吞吐量最大化的功率分配和能量转移策略.该策略在最大化系统端到端的吞吐量条件下,根据能量和数据因果约束,构建了系统吞吐量优化模型,在满足传输节点间能量和数据因果关系约束条件下,求得最优解;应用延迟策略将问题分解为最优功率分配和逐个时隙的能量转移问题,分别使用定向注水算法和不等式分析求解,原问题的最优解则通过分离的两个问题的解来获得.仿真结果表明,与基于单向能量协作和双向能量协作的功率分配和能量转移策略相比,本文提出的策略能够显著提高系统吞吐量.




5 仿真结果




6 结束语

