2020年高考数学选做题预测

王佩其

众所周知，新课标高考全国卷数学试题的最后一题，是一个分值为10分的选做题，要求二选一作答，其中一题考查坐標系与参数方程内容，另一题考查不等式选讲内容. 从命题形式来看，两个题目都是具有两小问的解答题;从难度上看，以中档题为主;从考查目标来看，主要考查考生的逻辑推理能力和数学运算素养.

高考命题一向坚持稳中有变不断创新的原则. 在2020年的新课标高考数学的全国卷中，选做题会如何命题，本文分坐标系与参数方程和不等式选讲两个部分加以预测，供考生参考.

一、坐标系与参数方程

（一）考纲回眸

1. 了解坐标系的作用，了解在平面直角坐标系伸缩变换作用下平面图形的变化情况;

2. 了解极坐标的基本概念，会在极坐标系中用极坐标刻画点的位置，能进行极坐标和直角坐标的互化;

3. 能在极坐标系中给出简单图形表示的极坐标方程.

4. 了解参数方程，了解参数的意义;

5. 能选择适当的参数写出直线、圆和椭圆的参数方程.

（二）命题规律

高考对坐标系与参数方程考查主要有以下两方面：

（1）参数方程、极坐标与曲线的关系;

（2）由参数方程、极坐标方程求解曲线的一些基本量，主要是极坐标与直角坐标、参数方程（直线、圆、椭圆的参数方程）与普通方程的互化问题及应用等，考查知识点较为简单和稳定.

（三）试题预测

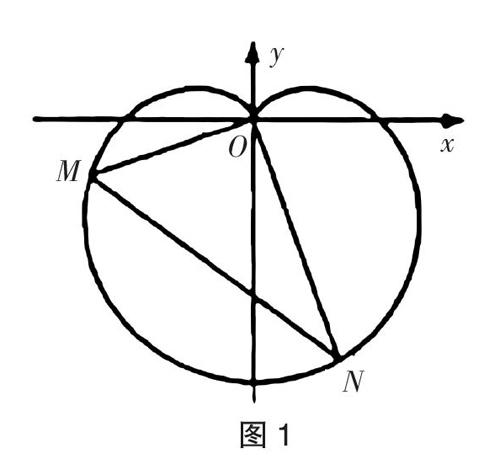
【预测题1】在新中国成立周年国庆阅兵庆典中，众多群众在脸上贴着一颗红心，以此表达对祖国的热爱之情. 在数学中，有多种方程都可以表示心型曲线，其中有著名的笛卡尔心型曲线. 如图1，在直角坐标系中，以原点O为极点，x轴正半轴为极轴建立极坐标系. 图中的曲线就是笛卡尔心型曲线，其极坐标方程为ρ=1-sin？兹 （ρ=1-sin？兹， ρ>0），M为该曲线上的任意一点.

（1）当 | OM | =■时，求M点的极坐标;

（2）将射线OM绕原点O逆时针旋转■与该曲线相交于点N，求 | MN | 的最大值.

【详细解答】（1）设点M在极坐标系中的坐标（■，），

由ρ=1-sin，得■=1-sin，sin=-■. ∵ 0≤<2？ ■或=■.

所以点M的极坐标为（■， ■）或（■， ■）.

（2）由题意可设M（ρ1， ？兹），N（ρ2， ■）.

由ρ=1-sin得ρ1 =1-sin，ρ2 =1-sin（■+=1-cos

| MN |=■=■=■=■，

■时，| MN | 的最大值为■+1.

【考点说明】本题背景新颖，主要考查极径的几何意义，三角函数的性质，利用极径的几何意义是解题关键，属于基础题.

【预测题2】在平面直角坐标系中，曲线C1的参数方程为x=4cos，y=2sin（为参数），曲线C2的参数方程为x=1+cos，y=sin（为参数）.

（1）求曲线C1直角坐标方程以及C2的极坐标方程.

（2）若A（ρ1， ），B（ρ2， +■） 是曲线C1上的两点，求■+■的值.

【详细解答】（1）由题可得C1的普通方程为■+■=1，C2的普通方程为（x-1）2+y2=1，

∴将x= ρcos，y= ρsin代入C2的普通方程化简得C2的极坐标方程为ρ=2cos.

（2）将x= ρcos，y= ρsin代入C1的普通方程化简得C1的极坐标方程为■+■=1，

将A（ρ1， ），B（ρ2， +■） 代入，得■+■=1，■+■=1，

∴ ■+■=（■+■）+（■+■）=■.

【考点说明】本题考核参数方程和普通方程的互化，直角坐标方程和极坐标方程的互化，考查了极坐标方程的应用，是基础题.

【预测题3】在以原点为极点，x轴正半轴为极轴的极坐标系中，曲线C1的极坐标方程为ρ2 cos 2？兹+8ρcos？兹=ρ2+8.

（1）求曲线C1的直角坐标方程;（2）曲线C2的方程为x=2+ tcos，y= tsin（t为参数），若曲线C1与曲线C2交于A、B两点，且 | AB | =8，求直线AB的斜率.

【详细解答】（1）由ρ2 cos 2+8ρcos=ρ2+8得ρ2 （2cos 2 -1）+8ρcos=ρ2+8，2ρ2 cos 2 +8ρcos=2ρ2+8，于是2x2 +8x=2x2 +2y2 +8.

∴ 曲线C1的直角坐标方程为y2=4（x-1）.

（2）曲线C2是直线. 且过点P（2，  0），倾斜角是？琢，将其参数方程代入曲线C1的方程得：t2sin 2 -4tcos？兹-4=0，∴ t1+t2=■，t1 t2=-■，于是 | AB | = | t1-t2 | =■=8，即（■）2-4（-■）=64，解得sin 2 ■，即sin■，∴ ■或=■，∴ k=tan=1或k=tan=-1，于是AB的斜率为 ±1.

【考点说明】本题考查极坐标方程和直角坐标方程之间的转换，一元二次方程根和系数关系式的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型.

【预测题4】已知直线l过点（1， 0），倾斜角为60°，在以坐标原点为极点，x轴的非负半轴为极轴的极坐标系中，曲线C的方程为ρ2=■.

（1）写出直线l的参数方程和曲线C的直角坐标方程;

（2）若直线l与曲线C相交于A、B两点，设点F（1， 0），求■+■的值.

【详细解答】（1）∵直线l过点（1， 0），倾斜角为60°，

∴可设直线l的参数方程为x=1+■t.y= ■t（t为参数），

∵曲线C的方程为ρ2=■，∴ 2ρ2+ρ2sin 2 =6，

∴ 2（x2 +y2 ）+y2=6，即2x2 +3y2 =6，∴曲線C的直角坐标方程为■+■=1.

（2）由（1）知，直线l的参数方程为x=1+■t，y= ■t（t为参数），A、B两点所对应的参数分别为t1，t2，将的参数方程代入到曲线C的直角坐标方程为■+■=1中，化简得：

11t2+8t-16=0，∴由韦达定理，得t1+t2=-■，t1t2=-■，

∵ t1·t2=-■<0，∴ | FA |·| FB | = | t1·t2 |=■.

| FA | + | FB | = | t1 | + |t2 |=| t1-t2 | =■=■=■ ，

∴ ■+■=■=■.

【考点说明】本题综合考查了极坐标方程，参数方程，韦达定理的应用，意在考查学生的计算能力，利用直线的参数方程可以简化运算，是解题的关键. 属于中档题.

【预测题5】在平面直角坐标系xOy中，曲线C1：x=2cos，y= sin？（？茁为参数），将曲线C1上所有点横坐标缩短为原来的■，纵坐标不变，得到曲线C2，过点（0， -■）且倾斜角为？琢的直线l与曲线C2交于A、B两点.

（1）求曲线C2的参数方程和？琢的取值范围;（2）求AB中点P的轨迹的参数方程.

【详细解答】 （1）曲线C2的参数方程为x=cos，y= sin（为参数）

当=■时，l与C2交于两点;当≠■时，记tan？琢=k，则l的方程为y=kx-■，l与C2交于两点当且仅当 |■| <1，解得k<-1或k>1，即？（■， ■）或∈（■， ■）.

综上，？琢的取值范围是（■， ■）.

（2）l的参数方程为x= tcos，y= -■+tsin（t为参数，■<）.

设A、B、P对应的参数分别为tA、tB、tP，曲线C2的普通方程为x2 +y2 =1，

将直线l的参数方程与曲线C2的普通方程联立得t2 -2■tsin+1=0，

则tP=■，且tA、tB满足t2 -2■tsin+1=0.

于是tA+tB=2■sin，tP=■sin，

又点P的坐标（x， y）满足x= tP cos？琢，y= -■+ tP sin

所以点P的轨迹的参数方程是x=■sin2，y= -■-■cos2（为参数，■<）.

【考点说明】本题考查伸缩变换、曲线的参数方程的求解以及动点轨迹参数方程的求解，涉及直线参数方程几何意义的应用，考查计算能力，属于中等题.

二、不等式选讲

（一）考纲回眸

1. 理解绝对值的几何意义，并了解下列不等式成立的几何意义及取等号的条件：| a+b|≤| a |+| b|（a， b∈R）;| a-b|≤| a-c|+| c-b|（a， b，c∈R）;

2. 会利用绝对值的几何意义求解以下类型的不等式：|ax+b|≤c;|ax+b|≥c;|x-c|+|x-b|≥a.

3. 通过一些简单问题了解证明不等式的基本方法：比较法、综合法、分析法.

（二）命题规律

高考对不等式选讲的考查主要有以下两个方面：

（1）绝对值不等式的求解与函数问题的综合，这是高考命题的热点;

（2）绝对值不等式中的恒成立问题与不等式的证明相结合.

（三）试题预测

【预测题1】已知函数f（x）= |2x-3| + |2x+1|.

（1）解不等式：f（x）≥6;（2）设x∈R时，f（x）的最小值为M. 若正实数a， b，c满足a+b+c=M，求ab+bc+ca的最大值.

【详细解答】（1）当x≤-■时，不等式化为-2x+3-2x-1≥6，解得x≤-1;

当-■< x <■时，不等式化为-2x+3+2x-1≥6，解得x∈？准;

当x≥■时，不等式化为2x-3+2x+1≥6，解得x≥2;

综上，不等式的解集为（-∞， -1]∪[2， +∞）.

（2）由 |2x-3| + |2x+1|≥|（3-2x）+（1+2x）|=4，

所以f（x）的最小值M=4，∴ a+b+c=4，

因为a2+b2 ≥2ab，b2+c2 ≥2bc，c2+a2 ≥2ca，

可得a2+b2 +c2≥ab+bc+ca，当且仅当a=b=c取等号.

所以 3（ab+bc+ca）≤（a+b+c）2=16？圯ab+bc+ca≤■，当且仅当a=b=c取等号.

故ab+bc+ca 的最大值为■.

【考点说明】本题主要考查了含绝对值不等式的求解，以及绝对值三角不等式的应用，其中解答中熟记绝对值不等式的解法，以及合理应用绝对值的三角不等式是解答的关键，着重考查了推理与运算能力，属于基础题.

【预测题2】已知函数f（x）= | x-5| + | x-3|.

（1）求函数f（x）的最小值m;（2）若正实数a ， b满足a2+■=m，证明：■+■≥2.

【详细解答】（1）f（x）= | x-5| + | x-3|≥|（x-5）-（x-3）|=2，

所以函数f（x）的最小值m=2.

（2）由（1）知a2+■=2，因为（■+■）2=■+■+■，

所以■+■+■=■×（a2+■）×（■+■+■）=■×（■+■+■+■+2），

因为■+■≥2，■+■≥4（当且仅当b=2a 时取等号），

所以（■+■）2≥■×（2+4+2）=4（当且仅当b=2a 时取等号），

即■+■≥2（当且仅当b=2a 时取等号），当b=2a ，a2+■=2时，解得a=1，b=2，

即■+■≥2（当且仅当a=1，b=2时取等号）.

【考点说明】本题考查绝对值不等式公式| a |+| b|≥| a-b|以及基本不等式的应用，是中档题.

【预测题3】已知函数f（x）=2| x+1| + | x-2|，f（x）的最小值为M.

（1）求M;（2）若a>0，b>0且a+b=M，求■+■的最小值.

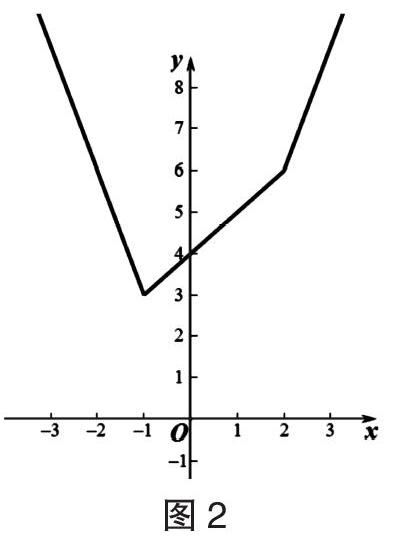
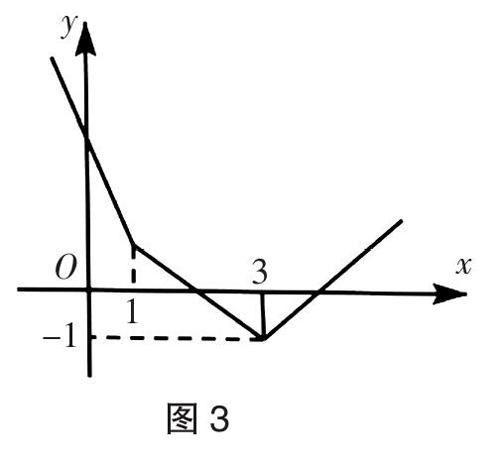
【详细解答】（1）f（x）=2| x+1| + | x-2|=-3x， x≤-1x+4， -1

函数f（x）的图像如图2所示：

∴ f（x）min = f（-1）=3.

（2）由（1）可知a+b=3，故

■+■=■[（3a+b）+（a+3b）]·（■+■）=■（2+■+■）. 又a>0，b>0，∴■>0，■>0，

∴ ■+■≥2，∴ ■+■≥■，当且仅当a=b=■时“=”成立，

∴ ■+■的最小值为■.

【考点说明】本题主要考查了利用基本不等式求最值以及利用图象法解绝对值不等式，属于中档题.

【预测题4】已知函數f（x）= | x-3| + | x-1|.

（1）若f（x）≥x+m对任意x∈R恒成立，求实数m的取值范围;

（2）记函数f（x）的最小值为s，若a，b，c>0，且a+b+c=s，证明：4ab+bc+ac≥8abc.

【详细解答】（1）设g（x）= f（x）-x = | x-3| + | x-1| -x，

∵ g（x）≥m恒成立

∴ g（x）=x-4， x≥3-x+2，  1

故g（x）min = g（3）=-1，

∴ m∈（-∞， -1].

（2）f（x）= | x-3| + | x-1|≥

|（x-3）-（x-1）|=2，

当且仅当1≤x≤3时等号成立，∴ s=2，即a+b+c=2，

原不等式等价于■+■+■≥8，由柯西不等式得：

（a+b+c）（■+■+■）≥（■·■+■·■+■·■）2 =16，

∴ ■+■+■≥8，当且仅当a=■，b=■，c=1时等号成立，

∴ 4ab+bc+ac≥8abc成立.

【考点说明】本题主要考查了含绝对值不等式的求解，以及含绝对值不等式的恒成立问题，其中解答中合理分类讨论去掉绝对值，转化为等价不等式求解是解答的关键，着重考查了分类讨论思想，以及推理与运算能力，属于中档试题，

【预测题5】已知函数f（x）=x2-x+1，且a，b，c∈R.

（1）若a+b+c=1，求f（a）+f（b）+f（c）的最小值;

（2）若 | x-a |<0，求证：| f（x）-f（a）|<2（| a |+1）.

【详细解答】（1）由柯西不等式，得a2+b2 +c2≥■（a+b+c）2 =■（当且仅当a=b=c=■时取等号），所以f（a）+f（b）+f（c）=（a2+b2 +c2）-（a+b+c）+3≥■+1=■，

即f（a）=f（b）=f（c）的最小值为■.

（2）因为 |x-a|<1，所以 |f（x）-f（a）|=|（x2-a2）-（x-a）|=|x-a |· | x+a-1| <| x+a-1| = |（x-a）+（2a-1）|≤| x-a |+| 2a-1|<1+（2| a | +1）=  2| a | +1，故结论成立.

【考点说明】本题考查了利用柯西不等式求最值，考查了利用绝对值三角不等式证明的问题，属于中等题.

责任编辑 徐国坚