非高斯噪声下的回声消除算法研究*
杨瑞丽,潘 琛
(商丘工学院信息与电子工程学院,河南 商丘476000)
1 引 言
通话质量问题是在人们的通信的过程中广受关注的几个具有决定性的核心问题之一,其中通话的噪声和回声一直都是人们认为影响电话通信质量的主要决定性因素[1-2]。针对此类问题,已出现了比较成熟的回声消除技术, 基于自适应滤波的回声消除器就是被广为认可和应用的一种回声消除典型技术,该类技术通过有限长脉冲响应滤波器(FIR)进行建模[3],得以实现的前提是假设回声路径符合线性特征。基于自适应滤波的回声消除技术常用的算法有最小均方误差(Least Mean Square, LMS)算法和归一化最小均方误差(Normalized Least Mean Square, NLMS)算法等。
目前,虽然针对回声消除的自适应滤波算法研究已经比较常见,但大部分研究是基于高斯噪声背景进行的。在日常生活的现实和虚拟世界中, 由于雷电、飓风、天电干扰、太阳磁暴和宇宙电磁波脉冲等自然因素,报警器、电动机、柴油机、发动机、发电机等人为因素的相互影响,在对语音信号的处理、实时道路交通的检测等复杂应用场合中,普遍存在的不是只有符合高斯分布的噪声,另一种非高斯所产生的噪声同样也广泛地存在着[4]。非高斯噪声往往都会在环境中呈现出很强的电磁波脉冲分布特性,与高斯分布的噪声相比, 往往表现为分布更为厚重的噪声拖尾现象。高斯噪声和非高斯的噪声都有可能被用来作为回声消除系统的主要背景噪声。
正是由于复杂环境所产生的非高斯噪声往往具有特殊的特性,比如强烈的冲激性,严重地影响基于 范数优化准则的各种自适应噪声滤波系统和算法的性能。除此之外,通信系统中的回声路径通常都具有明显的稀疏特性[5-6],在核心矩阵算法的理论基础上与回声消除系统的稀疏特性相互结合,可以有效地大幅度降低算法的计算量和成本,根据此特点,文献[7]利用比例矩阵思想,设计了修正的改进比例归一化最小均方误差(Modified Improved Proportionate Normalized Least Mean Square,MIPNLMS)算法。根据符号算法(Sign Algorithm, SA)对非高斯噪声具有良好适应能力这一特点。在此将改进比例矩阵算法的思想融合应用到符号算法中,提出一种不仅适用于高斯噪声,更能消除非高斯噪声的改进MIPNSA 算法,并将该归一化算法应用于修正噪声的回声消除的系统中,从而使回声消除系统能够较好地消除不同背景下的回声。
2 非高斯噪声条件下的新算法
高斯的和非高斯的噪声都有可能被用来作为回声消除系统的主要背景噪声。非高斯噪声所表现的脉冲特性,严重影响了基于L2范数优化计算准则的自适应滤波算法的回声消除性能,现已有研究工作明确论证了符号矩阵的算法能够有效抑制非高斯的噪声[8]。同时,回声路径矩阵也具有明显的稀疏特性,该特性同样影响自适应滤波算法对回声消除的性能。综上分析,考虑高斯与非高斯两种噪声作为回声消除的背景噪声,可将比例式滤波矩阵的设计思想与NSA 算法相结合,设计出适用于非高斯噪声背景下实现回声消除的改进MIPNSA 算法,其中采用α 稳定分布表述非高斯分布的方法描述非高斯噪声。
在非高斯噪声背景下,NSA 算法[9]因具有良好性能而被广泛应用,该算法是通过将NLMS 算法和SA 算法相结合而得到的,不仅保留了NLMS 算法所具有的收敛速度快的特点,同时又对非高斯噪声具有良好的抑制能力,设滤波器系数向量为hˆ(n),系统的输入向量为x(n),误差信号为e(n),固定步长参数为μ,则NSA 算法的主要的迭代函数方程可以表示为下式:

已发表的回声消除相关研究工作表明,自适应滤波器的阶数、收敛步长、系统稀疏度等都是影响自适应滤波算法性能的主要因素[10]。关于系统稀疏度与算法性能之间的算法研究亦较为成熟,已知现有的IPNLMS 算法对系统的稀疏特性则具有良好的适应能力,该算法是在PNLMS 算法的基础上针对系统稀疏度进行改进而提出的。设有对角矩阵G(n),指正参数ζ 和φ,则IPNLMS 主要的迭代函数方程为:

把式(2)中系数比例矩阵带入如(1)式所示的SA算法迭代公式中,整理为迭代方程可表示为如下式的IPNSA 算法:

根据式(2),系统比例项权重会直接影响IPNLMS算法的收敛速度。文献[7]的MIPNLMS 算法给出了系统比例项的权值与整个系统稀疏度的关系表述,但MIPNLMS 算法并没有明确系统比例项的权值取最优时系统稀疏度的取值。




令γ 和δ 分别表示正参数,则β(n)可表示为:

设MIPNLMS 算法中的对角矩阵为K(n),根据(4)、式(5)、式(6),K(n)可表示为:
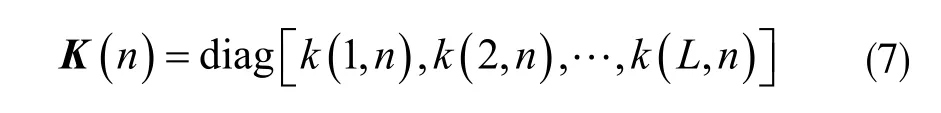
已知式(7),则MIPNLMS 算法迭代更新函数可表示为:

根据式(8),结合式(1),可将改进的MIPNSA 算法的迭代更新函数表示为:

根据迭代更新函数式(9),所提的改进MIPNSA算法在输入非高斯噪声后可以表示为如下各式所示的自适应过程:

3 仿真实验
3.1 仿真条件
仿真实验所采用的输入信号包括两种形式,即随机信号和相应的语音信号。将两种输入信号分别进行相应的MATLAB 仿真。在仿真实验中,FIR 滤波器的长度等于128,并使线性的声学回声路径的长度为128。
设脉冲响应的长度为L,以r(n)表示范围为[-0.2,0.2]的随机数,δ 为Dirac 函数,初始状态令L=128,初始化hˆ(n)为零向量,根据下式即可计算线性声学回声路径:

其中,n,i=0,1,...,L-1。
回声路径的特性如图1 所示,具有明显的稀疏特点,其中系数较大的数值只占少数,系数较小的数值占大部分,并且大部分接近零。

图1 声学回声路径脉冲响应h
3.2 性能指标和参数设置
实验进行的条件是各对比算法取等效步长,各种算法实验结果的综合性能表现好坏利用权误差向量范数(WEVN)的收敛曲线函数来准确衡量和分析评价, 从而充分说明各种算法综合实验性能的总体优劣。
线性系数的WEVN 表达式为:

随着WEVN 的取值的变小,即表示系统中的自适应滤波器和所需要跟踪的未知滤波器系统越来越逼近。
设分散系数为γ,令高斯环境下的信噪比为SNR1,非高斯环境下的信噪比为SNR2,分别表示为如下二式:

仿真实验将高斯条件和非高斯滤波噪声两种条件下的滤波信噪比分别精确设置为20dB,其中输入的非高斯噪声取α=1.5 时具有稳定分布。
3.3 仿真结果分析
在进行仿真实验时,每个实验仿真结果统一采用30 次独立仿真实验的平均结果,符合实验的公平原则。
3.3.1 随机信号仿真实验
仿真实验中输入信号为高斯白噪声,均值为零。当输入高斯噪声时,各算法性能比较如图2 所示;当输入非高斯噪声时,各算法性能比较如图3 所示。
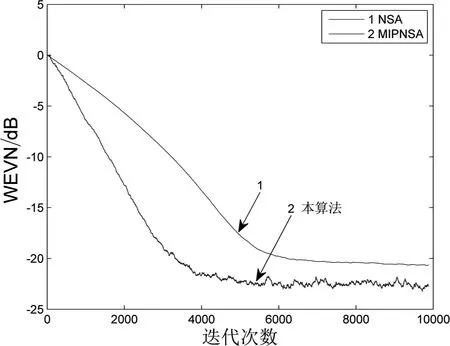
图2 高斯噪声下滤波器系数收敛曲线(随机信号)

图3 非高斯噪声下滤波器系数收敛曲线(随机信号)
对比图2 和图3 中的仿真结果,可以明显看出:在非高斯噪声的条件下,传统算法的回声消除已经开始出现失效。此外,与其他各类传统高斯噪声算法相比,此处提出的改进MIPNSA 算法不管是在高斯噪声环境下还是非高斯噪声的环境下,回声消除效果均表现较好。
3.3.2 语音信号仿真实验
仿真实验中采集非平稳的真实语音信号作为系统的输入信号,输入的语音信号如图4 所示,该信号是样本长度为20000 和频率长度为4kHz 的采样噪声,其他参数的取值与均值为零的高斯白噪声相同。

图4 语音信号
两种噪声条件下的滤波器系数收敛曲线如图5和图6 所示。
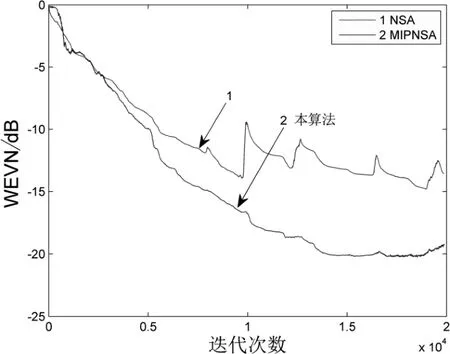
图5 高斯噪声下滤波器系数收敛曲线(语音信号)

图6 非高斯噪声下滤波器系数收敛曲线(语音信号)
对比如图5 和图6 中的仿真结果,可明显看出:当语音信号作为滤波器的输入信号时,在高斯噪声和非高斯噪声两种环境下,根据不同滤波器算法的非平稳收敛曲线,仍然能够反映本改MIPNSA 算法对高斯噪声和非高斯噪声的消除效果。虽然语音信号作为输入时的非平稳的特性直接导致本算法的收敛曲线性能比预期有所降低,但相比于实验中其他算法的仿真结果,本算法对非高斯噪声的效果仍然表现较好。
4 结 束 语
随着通信技术和多媒体处理技术的不断发展,社会对便利性、互动性日益增长,一般的通信质量已经难以满足人们的日常需求。在通信质量的各种指标中,语音清晰度是最基本也是最主要的一点。为保证语音清晰度,最关键是要更好地去除回声和噪声的影响。通过实验,分别采用随机信号和语音信号作为回声消除系统的输入,对高斯噪声和非高斯噪声实验仿真的结果进行分析,可以得出以下结论:一、所提的MIPNSA 算法能够适用于不同类型和背景的噪声,对高斯噪声和非高斯噪声均能够表现出较好的抑制噪声能力;二、明确系统的稀疏性与比例项的权值两者之间的关系,便可更好地实现自主控制系统比例项的权重,并对其进行适当的选值,使得算法能够进一步改善回声消除的效果。相较于仿真实验中采用的传统自适应滤波算法,所提的新算法具有更快的收敛速度以及更佳的系统稳态性能。

