材料漫反射比测量研究综述

马宇轩，冯国进，孙若端，甘海勇，郑春弟，吴厚平，张巧香，刘子龙

(中国计量科学研究院，北京 100029)

引言

在日常生活中，反射现象无处不在，人或动物能够看清物体的全貌主要是依赖反射光在眼睛内的成像。在各类反射现象中，漫反射是指光线被粗糙表面无规则地向各个方向反射的现象，占反射的主体部分。材料的光谱漫反射特性对于光度学、辐射度学以及色度计量等领域具有重要意义，在照明工程、生物医药、建筑业、遥感科学、辐射定标技术以及空间探测领域都有着重要的应用[1]。投光照明是景观照明中最常用的照明手段，只有知道了被照对象材料的漫射特性才能达到设计的照明效果。在计量领域，材料漫反射比被国际光度和辐射度咨询委员会(CCPR)定为光辐射领域的6个关键性比对物理量(比对代号：K5)之一，受到了各国计量机构的重视。漫反射比测量的水平高低直接代表了该国在该领域的计量能力，因此，如何改进测量方法，优化测量步骤，以提高漫反射比的测量水平，降低漫反射比测量结果的不确定度一直是各国不断努力的目标。

1 材料漫反射比的测量方法

材料漫反射测量方法从大类上讲分为相对测量法和绝对测量法。相对测量法主要适用于常规性、大批量或精度要求不太高的场合下的测量。绝对测量法一般适用于计量机构，用于量值的复现和高等级的测量，尤其在国际比对等关乎国际声誉的场合下使用较多。

1.1 相对测量法

相对测量法的测量不确定度水平依赖于标准样品的漫反射比的不确定度。相对测量法的原理图如图1所示，在样品位置依次放置待测样品和已知反射比的标准漫反射板进行测试。

图1 相对测量原理图Fig.1 Schematic diagram of relative measurement

该方法最终测得的反射比R为

(1)

其中，S1、S2分别为测量待测样品以及标准样品时得到的测量信号，RS为已知反射比的标准样品。该方法要求：积分球内壁必须由漫射特性较好的高漫反射比材料制成；待测样品和标准样品的的反射特性要尽可能接近理想朗伯体，以降低由于空间反射分布不同造成的系统误差。

1.2 绝对测量法

漫反射比的绝对定标方法很多，国际上比较公认的绝对测量方法主要有三种：夏普-利特法(Sharp-Little)[2]、科特法(Korte)、辅助积分球法，也是各国家计量院(NMI)采用的方法，他们大多在上世纪均已经完成相关装置的搭建。

1)夏普-利特法(Sharp-Little)。1920年，泰勒提出了将积分球引入到材料漫反射比测量中的方案，成功实现了d/d(漫射光入射，积分球探测)和0/d(入射光垂直于样品表面入射，积分球探测)条件下的漫反射比的测量[3]。1920年，Sharp和Little同样将积分球引入漫反射比测量中，并在此基础上引入了挡屏，成功实现了d/0(用积分球产生漫射光入射到样品表面，垂直于样品表面探测)条件下漫反射比的测量。1970年，Budde对Sharp-Little的方法进行更严密的论证，修正了积分球开口处的误差，建立了d/0条件的漫反射比测量装置[4]。

夏普-利特法的测量原理[5]如图2所示，积分球内表面为反射率高、漫反射性能好的白色涂层。当一束入射辐射通量为Φ的光由开口进入积分球照射到内壁A处，经过涂层表面的一次或多次漫反射后,一部分光通量会经由开口出射, 其他光通量则会在积分球内壁上形成均匀照度。

图2 测光积分球原理示意图[5]Fig.2 Schematic diagram of optical integration sphere

设球内B点的照度为E，它由A点出射的直射照度E0和多次漫反射照度EΣ这两部分组成,B点的总照度为[6]：

(2)

其中ρ为积分球内表面涂料的光谱反射比，F为实际内反射面积与积分球内表面面积之比。

在A、B点之间引入挡屏，当挡屏存在时，A点直射到B点的照度被完全遮挡，此时B点的照度就只有E∑，由此得出

(3)

通过式(3)将光谱漫反射比的测量转化成对于该点的漫反射照度与总照度的测量以及积分球几何参数F的计算。

2)科特法(Korte)。该方法的特点是样品位于积分球球中心，但只采用积分球半球对样品进行漫射照明。

科特利用了理想漫反射体各方向、各个波长上的反射因数均匀的特点，将对理想漫反射体的亮度测量转换成对施加辐照的半球球壁亮度的测量。

图3为科特法的原理图，其中L为光源，用以对半球Ⅱ进行照明，P为挡屏，避免光源对半球Ⅰ进行直接照射。半球Ⅰ所接收到的光源是以半球Ⅱ作为二次光源进行照明的。探测器通过测量孔分别对半球Ⅰ和半球Ⅱ的亮度进行测量。

图3 科特法测量原理图[5]Fig.3 Schematic diagram of Korte measurement

该方法测得的漫反射比ρ为

(4)

式中LⅠ和LⅡ分别为半球Ⅰ和半球Ⅱ测得的亮度。

这种方法的优点在于它摆脱了复杂的公式推导，使测量结果直观地展示出来。缺点在于该方法将光源放置在积分球内部，对于积分球的体积要求增大了，并且随着时间的推移，球内温度会升高，所以需要配备相应的冷却系统以及复杂的机械移动装置，导致测量与加工的难度增大。

3)辅助积分球法。辅助积分球法又称为双球法，该方法需要用到单孔辅助积分球和平面漫反射板，其中单孔辅助积分球所用的内壁材料以及制作工艺均与平面漫反射板完全相同。其测量原理如图4所示。

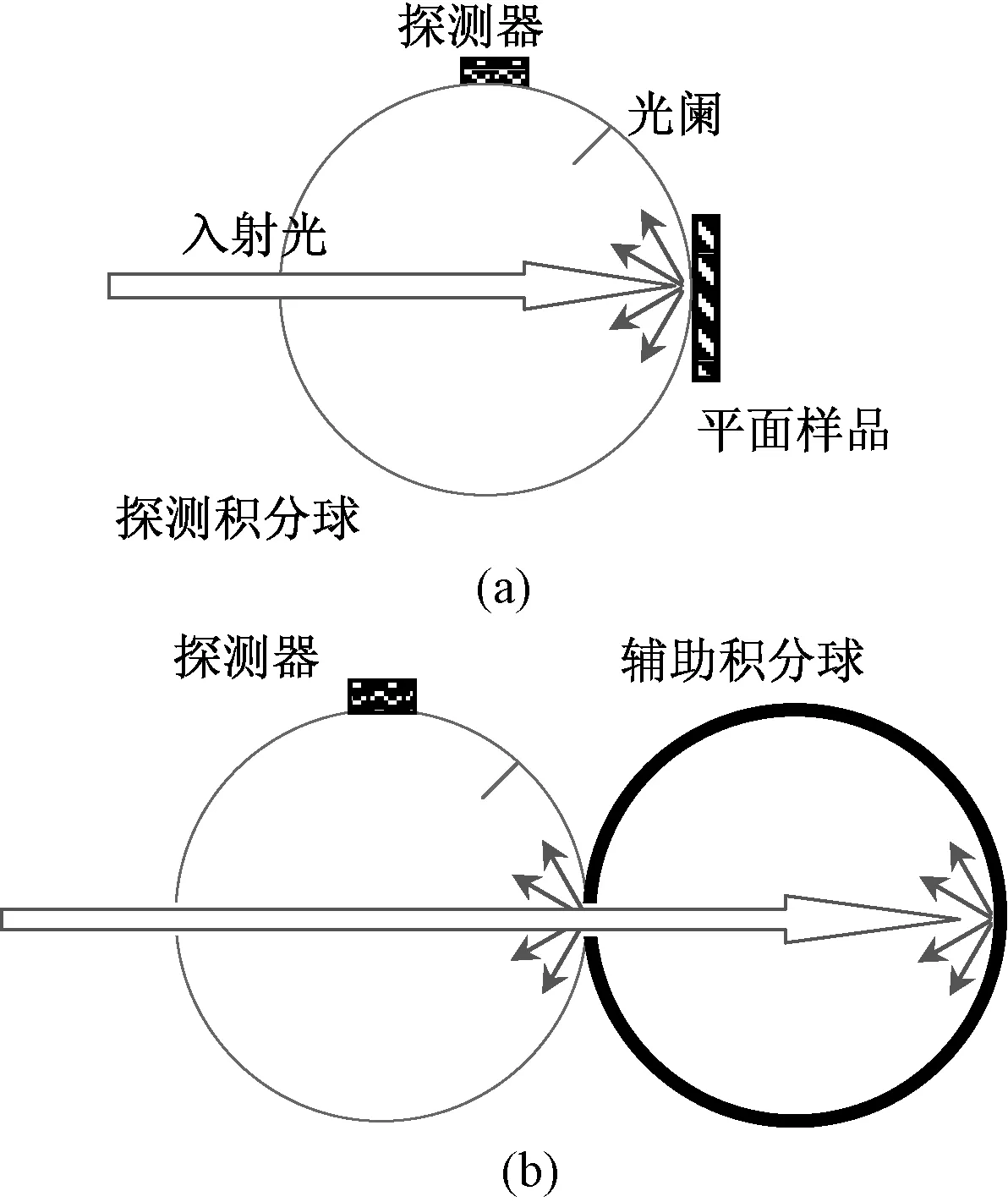
图4 辅助积分球法测量原理图[5]Fig.4 Schematic diagram of auxiliary integration sphere

图4(a)是将平面漫反射板作为样品，图4(b)是将辅助积分球作为样品。该方法得出的漫反射板的光谱反射比ρ为

(5)

其中，QF和QS依次为测量出的辅助积分球和漫反射板的相对反射比[7]。f为辅助积分球开口处球冠面积与内表面总面积的比值。

通过这种方法可以将漫反射比测量问题转化为对于辅助积分球几何参数的测量以及辅助积分球和漫反射板的光电读数问题。

这种方法相比于前面两种方法操作更为简单。但在实际测量中，有诸多因素会对实验结果造成影响，例如，辅助积分球内表面反射比均匀性的影响, 辅助积分球开口的影响,辅助积分球开口边缘厚度的影响等。

4)其他方法。目前，少数国家正在尝试采用双向反射分布函数(BRDF)的方法进行漫反射比的绝对测量，该方法可以准确地反映材料在2π空间的光学反射特性，并且可以进行大面积、形状不规则样品的测量，但其不确定度水平等还有待进一步验证。

2 研究水平和现状

2.1 国际比对及研究水平现状

国际计量机构会定期在网站公布各个国家经过实际考核后的测量校准能力(CMCs)和国际比对进展。表1列出了几个国家在2008年进行的国际比对中的漫反射测量水平(波段范围为360～820 nm，间隔为20 nm)[8]。可以看出，以德国、美国为代表的国家在漫反射测量领域处于世界领先水平。

表1 CCPR-K5-2008 国际比对结果[8]

2.2 我国研究水平和现状

我国材料漫反射比量传和量值复现工作主要集中在中国计量科学研究院。中国计量科学研究院于20世纪80年代建立了0/d条件下800～2500 nm漫反射比国家副基准(不确定度U=0.4%,k=2)，于2000年利用改进的Sharp-Little法建立了d/0条件国家色度标准。并在此后对于诸多造成测量结果偏差的影响进行了修正与改进。2003年，对于积分球开口壁厚所造成的影响进行了分析，建立了数学模型对其进行修正[9]。2009年，通过对该公式的简化以及对于立体角精确的求解公式的计算，使得该修正方法更加严密简洁。当前在250～2 500 nm波段范围内，漫反射比测量不确定度水平可达0.4%(k=2)，和国际其他计量机构相比，测量能力基本属于同一梯队。

作为参与国际比对的成员之一，中国计量科学研究院当前正在进行新一轮的漫反射比国际比对(K5，波段范围为360～830 nm)，预计部分不确定度指标会有所提升。

3 结束语

在材料漫反射比的测量进程中，在20世纪基本已经形成了完善的并且通用的方法，此后做的很多相关的研究工作大多是在该基础上进行的细化、改进与修正。随着科技的发展和新材料的异军突起，许多行业对于漫反射比的测量精度和波段要求也进一步提高。为满足各行各业的需求，以中国计量科学研究院为代表的一批科研机构在2～16 μm的漫反射比量值复现方面已经获得初步成果，可以满足光学晶体材料研究、大气探测、空间探测等方面的需求，反射比低至0.00001的超低反射比测量装置也在组建中。材料漫反射比的测量正迎来新的发展机遇。