基于ELM的城市轨道交通系统建设成本估算研究

杨基宏，陈浩林，徐 刚，余澄庆，刘 辉

（1. 中车青岛四方机车车辆股份有限公司， 青岛 266111；2. 中南大学 数学与统计学院，长沙 410083；3. 中南大学 交通运输工程学院， 长沙 410075）

我国城市轨道交通行业发展迅速，成为国家“走出去”战略的重要产业代表。城市交通轨道系统的建设方便了人民出行，加速了城市间的经济文化交流。但其周期长，资金投入大，如何在建设施工过程中更好地控制成本已经成为亟待解决的问题。

目前，众多领域均有对大型项目建设成本的估算研究，王夏冰等人[1]利用BIM 数据信息平台实现自动化工程量计算和轨道交通建设过程的模拟，一定程度上避免了工程造价过高的情况；吕芳[2]提取与工程建设成本高相关的特征变量，结合分段回归预测和最小二乘拟合的方法对建设成本进行拟合和估算；孙亚南[3]构建动态成本估算模型，采用粒子群算法进行优化迭代，用以对待选方案进行选择；杨磊等人[4]建立基于模糊神经网络和粒子群算法的高精度变电站全生命周期成本估算模型，算例证明该方法能够指导变电站建设方案的选取；刘敬严等人[5]利用BP 神经网络建立高铁建设环境成本估算模型，并以长益城际铁路为例验证了方法的精确性和适用性；段晓晨等人[6]结合显著性成本方法和人工神经网络对拟建工程的环境成本进行估算。

在城市轨道交通系统的建设成本研究领域，普遍采用工程管理的方法对建设成本进行定性分析，或是提出控制成本的思考和定性的管理方法。本文利用机器学习算法，通过城市轨道交通系统建设阶段的少量关键成本指标，建立城市轨道交通系统建设成本估算模型，实现在设计阶段对建设成本进行估算的目标，为建设成本的控制与优化提供理论支撑。

1 基于ELM的模型构建

1.1 ELM概述

极限学习机（ELM ，Extreme Learning Machine） 是一种单隐层前馈神经网络学习方法[7]。ELM 简单易用，其输入权重和隐含层阈值均为随机确定，不需要经过迭代计算和更新，仅需设置隐含层节点个数，就可以通过求解线性方程组最小二乘解的方法获得输出权值，从而得到唯一最优解。ELM因学习速度快、泛化能力强、预测精度高被广泛应用于各领域[8-10]。ELM 网络结构如图1 所示。

图中，M为隐含层节点个数；wi为输入层到第i个隐含层节点之间的输入权重；βi为第i个隐含层节点到输出层的权重；i=1，2，…M。

1.2 ELM算法原理

假设ELM 网络有n个输入层节点，m个输出层节点，将采用的N个样本记为(xj,yj)，其中，xj=[xj1,xj2,xj3,…,xjn]T∈Rn为输入变量，yj=[yj1,yj2,yj3,…,yjm]T∈Rm为输出变量，j=1,2,3,…,N。则拥有M个隐含层节点的标准前馈神经网络的输出可以表示为：

其中，g(x) 为激活函数， 激活函数包括Sigmoid 函数、Threshold 函数和Liner 函数等；wi为输入层到第i个隐含层节点之间的输入权重，wi=[wi1,wi2,wi3,…,win]T∈Rn；bi为隐含层第i个节点的阈值；βi为隐含层第i个节点到输出层的权重，βi=[βi1,βi2,βi3,…,βim]T∈Rm；wi·xj则表示向量wi和向量xj的内积；i=1,2，…，M。

式（1）可以用矩阵表示为

其中，H为隐含层的输出矩阵，

对于已经随机赋值的输入权重wi和阈值bi，由式（2）可知，问题已经由训练模型转换为求解线性方程Hβ=Y的最小二乘解，记为。

其中，H -1为H的广义逆矩阵。

2 估算模型实例分析

2.1 建立成本数据集

通过参考文献[11] 得到8 条在运营城市轨道交通线路的建设成本数据，如表1 所示，包括前期准备成本、土建成本、车辆成本、车辆基地成本、机电设备成本、贷款利息、其他成本和延米造价。其中6条线路以地下敷设方式为主，包括北京4 号线、北京5 号线、北京10 号线、广州2 号线、南京1 号线和天津3 号线，2 条线路以地上敷设方式为主，包括北京八通线和北京13 号线。

根据前期准备成本、土建成本、车辆成本、车辆基地成本、机电设备成本、贷款利息和其他成本在城市轨道交通系统设计阶段获得的难易程度，以及成本特征的体量，基于尽量选择易获得且体量大的成本特征的原则，选择前期准备成本、土建成本、车辆成本和机电设备成本，共计4 个成本特征，作为基于ELM 的城市轨道交通系统建设成本估算模型的输入特征，延米造价为输出特征。

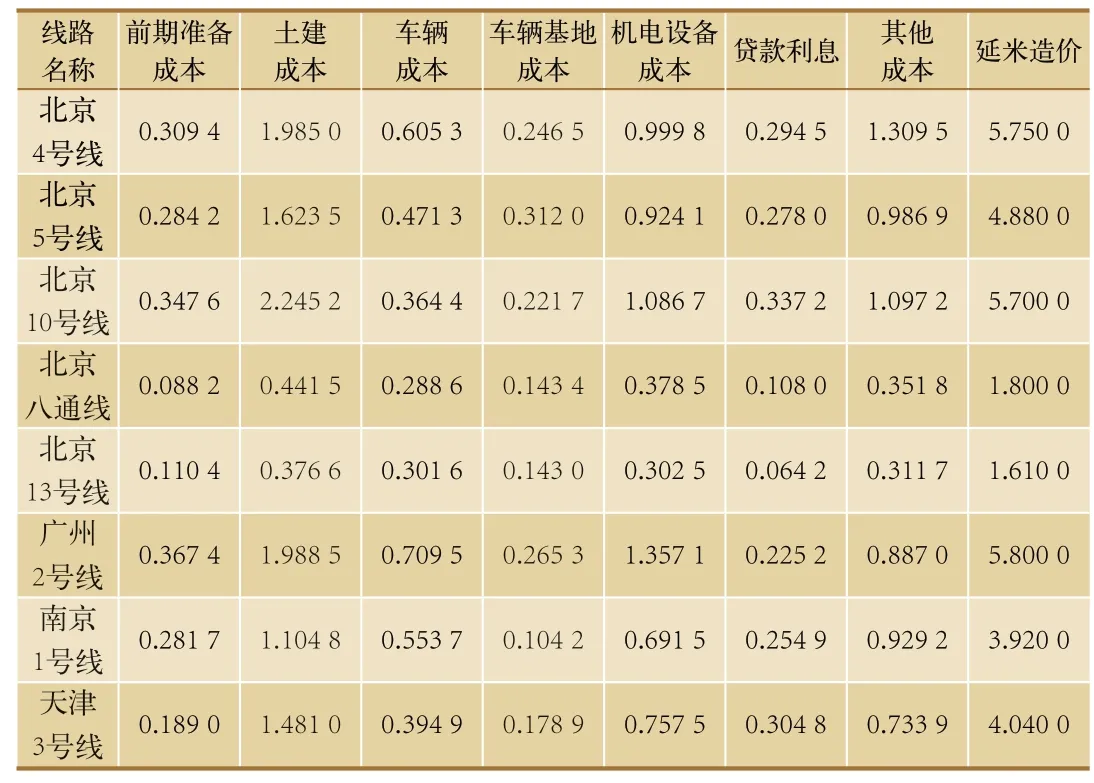
表1 线路建设成本数据表 单位：亿元/km

考虑到所获得的城市轨道交通线路数据较少，仅含8 条线路，不足以支撑ELM 模型的训练和验证，本文采用多项式拟合和添加噪声的方法生成轨道交通系统线路模拟数据。（1）采用多项式拟合的方法，对成本估算模型，每个特征4 个输入特征和1 个输出特征的8 个真实数据分别进行5 阶多项式拟合，得到5 个特征的趋势线。（2）对各特征趋势线添加代表轨道交通系统不确定性的白噪声，如图2 所示。直线x=i,i=1,2,3,…,700 与5 条特征趋势线交点的纵坐标即为第i条轨道交通系统线路的特征数据，其中8 条线路为真实数据，692 条线路为模拟数据。

考虑到多项式拟合所产生的特征趋势线与8 个真实特征数据在x轴上的相对位置相关，为了更科学地验证模型的估算性能和去除不确定性，本文对8 条真实城市轨道交通线路特征值在x 轴上的相对位置随机排序10 次，每次排序产生1 个成本数据集，共产生10 个成本数据集，分别用于成本估算模型的训练和测试。其中的3 个成本数据集如图2-4 所示。

2.2 估算模型程序化

本文基于Matlab 平台，选择成本数据集中的70条轨道交通系统线路的数据作为测试集，其余数据作为训练集。将每一条线路的前期准备成本、土建成本、车辆成本和机电设备成本作为输入，延米造价作为输出，利用训练集训练ELM 模型。设定ELM 模型的激活函数为Sigmoid 函数，隐含层节点个数为10。

利用10 个成本数据集，分别对基于上述设定的ELM 模型进行训练，获得10 个基于ELM 的城市轨道交通系统建设成本估算模型。将各数据集中的测试集分别输入相应的训练完成的模型中，得到各模型的估算结果以及估算误差。

本文采用均方误差（MSE ，Mean Square Error）、均方根误差(RMSE ，Root Mean Squared Error)、平均绝对误差(MAE ，Mean Absolute Error)和平均绝对百分比误差[12]( MAPE ，Mean Absolute Percent Error)来评价模型估算效果。

其中，m为测试集中样本的数量，为第i个样本的估算目标值，为第i个样本的估算值，i=1，2，…，m。建设成本估算模型的估算误差如表2 所示。

由表2 可知，10 个成本数据集中，MSE 最小值0.0423，最大值0.1036，平均值0.0615；RMSE 最小值0.2057，最大值0.3218，平均值0.2477；MAE 最小值0.1609，最大值0.2611，平均值0.2011；MAPE最小值4.35%，最大值7.23%，平均值5.62%。基于ELM 的城市轨道交通系统建设成本估算模型的最大MAPE 误差小于8%，平均MAPE 误差小于6%，估算结果在误差允许的范围内与实际数据吻合，能够实现城市轨道交通系统建设成本的高精度估算。

表2 成本估算模型估算误差列表

3 结束语

城市轨道交通系统建设成本估算的精确性对城市轨道交通系统全生命周期成本的优化与控制有着重大影响。本文提出的基于ELM 的城市轨道交通系统建设成本估算模型，可通过少量易获得的关键成本指标对建设成本进行估算。本文利用10 组成本数据集对估算模型进行验证，结果表明，该模型最大MAPE 误差不超过8%，与真实值较为接近。该方法能够为城市轨道交通系统建设成本估算提供一定的理论支撑。