基于灰色模型的铁路货运量预测

马睿　孟献刚

摘 要：文中利用灰色系统理论，以陕西省铁路货运为例，通过建立灰色GM（1，1）模型和改进数据序列光滑度的等维新息灰色模型，对陕西省铁路货运量进行分析研究和预测。通过分析两种模型的预测结果，得出改进的灰色模型预测精度更高，最后采用后验差检验等维新息灰色模型的精确度，并对未来三年的陕西省铁路货运量做出预测。

关键词：铁路货运;灰色模型;灰色预测;数据序列;后验差检验;预测精度

中图分类号：TP391 文献标识码：A 文章编号：2095-1302（2020）04-0-03

0 引 言

近年来，伴随着中国“一带一路”倡议的提出，我国与一带一路沿途国家的国际贸易合作更加紧密。国内外贸易快速发展，物流运输行业进入高速发展期，铁路货运运量大、运费低、能耗低、污染小的优势在各类物流运输行业中愈发突出。为了环境保护和可持续发展，政府部门一系列促进发展铁路运输的政策落地，我国货物运输整体结构不断优化调整，“公转铁”模式的运输结构逐渐影响并改变着物流体系，铁路货运发展势头有超越公路货运的趋势。铁路物流运输是绿色的物流货运运输方式，铁路物流运输为我国经济可持续发展和快速增长提供了强大的运力，为物流业的快速发展奠定了坚实的基础。如今铁路运输正在充分与地方物流运输和港口物流进行合作，同时也加快了与大型工矿企业合作以及物流园区铁路专线建设，向内采取调整优化，向外加快发展高铁等铁路基础建设这一系列措施都为铁路货物运输发挥铁路物流优势，扩大有效供给，降低物流成本，促进低碳绿色的交通运输提供了更强有力的保证。铁路货运量是反映铁路货物运输规模与发展速度的一项重要指标，为研究铁路物流运输的发展与变化趋势，本文以陕西省铁路货运为实例，通过对陕西省近年来的铁路货运量进行分析研究和预测，为判断陕西省铁路物流发展趋势提供定量的参考信息。灰色系统理论是我国学者创立的一种系统理论，是主要研究信息不足，样本数据较少的不确定性问题的方法[2]。灰色预测的特点是所需数据少，预测方法能够修正，预测精度较高，可以弥补在少数据、少信息基础上建模的一些不足。铁路货运相关数据较少，信息具有复杂的层次和随机的动态变化，基于铁路货运信息的特点，选择“贫信息”建模的灰色预测方法，运用灰色系统理论对铁路货运量进行分析研究具有可行性。

1 灰色模型建立

1.1 GM（1，1）模型建模

GM（1，1）模型是常用的灰色预测模型，建模过程如下：假设原始时间序列为n个原始非负样本序列，将X（0）作一次累加，生成

X（0）的1-AGO序列。其中：。由一次累加生成序列X（1）建立一阶线性微分方程，

其中a，b为参数，记。参数向量用最小二乘法估计，记为

其中矩阵Y，B：

，       （1）

估计出参数，后，得到预测模型为时间序列函数：

，k=2， 3， ...          （2）

其中。由上式累减可得原始数据系列模型，k=2， 3， ...，由此生成，其中。当k=1， 2， 3， ...， n时，是原始序列x（0）（k）的拟合值;当k>n时是原始序列x（0）（k）的预

测值。

1.2 等维新息GM（1，1）模型原理

GM（1，1）模型预测的精确度由于受到数据变化和时间序列长度的影响，对某些条件下的预测问题由于干扰因素积累会导致预测精度较差。等维新息模型的建模思想是用新陈代谢思想建模。建模过程是先通过GM（1，1）模型建模计算得到预测值，将预测值这个新信息加入到數据列中同时去掉原始序列中最早的旧信息，采用维数不变的新信息序列继续建立GM（1，1）模型。通过这样不断地计算预测，再不断地将新的预测值加入原序列，同时去掉最旧的信息，依次循环，反复重建相同维度的新信息数据GM（1，1）模型，最终通过新模型进行预测。

2 实例分析

在此以陕西省铁路货运量为实例，通过国家统计局数据库查询到陕西省2008—2018年铁路货运量总共11个数据，这里选择将前8个数据作为建模数据，后3个数据用于分析模型预测效果。

2.1 数据收集整理

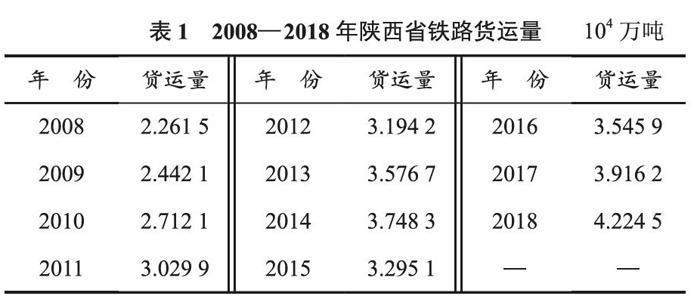
通过国家统计局数据库查询到的2008—2018年的陕西省铁路货运量列表如表1所示（数据来源：国家统计局数据库）。

2.2 各模型建模

以2008—2015年的陕西省铁路货运量数据为原始序列X（0），一次累加成1-AGO序列X（1）：X（1）=（2.261 5， 4.703 6，

7.415 7， 10.445 6， 13.639 8， 17.216 5， 20.964 8， 24.259 9）。

通过用Matlab 7.0编程计算出估计参数=（-0.056 1， 2.440 0），建立GM（1，1）模型即时间预测函数为：

（3）

用模型进一步计算出，累减还原得出，其中（2.261 5， 2.953 8， 3.124 1， 3.304 5， 3.495 1， 3.696 8， 3.910 1， 4.135 8）是2008—2015年陕西省铁路货运量拟合值，（4.374 4， 4.626 8， 4.893 8）是2016—2018年陕西省铁路货运量预测值。

在灰色理论中对GM（1，1）模型的改进方法一种是改进建模机制，一种是对原始数据列做数据处理，提高数据列光滑度。这里采用提高原始数据光滑度以及新陈代谢法对GM（1，1）模型进行改进并重建预测。本文采用用2008—2018年的数据通过Matlab 7.0拟合函数对数据进行处理。用拟合的函数y=0.003 5x3-0.070 6x2+0.586 2x+1.624 1计算出的数据序列光滑度比原始数据序列更平滑，其中2017年，2018年的货运量拟合计算结果为3.926 1×104万吨，4.188 2×104万吨，

与这两年实际数据的绝对误差分别为0.25%，0.86%，修正处理后的陕西省铁路货运量数据如图1所示。

用2013—2016年的铁路货运量拟合值替代实际值，以2011—2015年的铁路货运量为原始序列，将X（0）累加生成1-AGO序列X（1）建立GM（1，1）模型。通过用Matlab 7.0计算出估计参数为=（-0.089 7， 2.160 5），得到时间预测函数为：

（4）

用这个GM（1，1）模型计算出2016年货运量拟合值，再将该值加入到原数据序列X（0）中，同时去掉2011年旧数据，继续进行五维等维新息建模。依次通过4次等维新息建模，最终计算出2016—2018年的铁路货运量预测值为：。

2.3 各模型分析及预测结果比较

GM（1，1）模型是对原始数据基于最小二乘法做出的指数拟合的近似模型，数据越接近指数规律，序列越光滑预测效果越好。2015年我国宏观经济转型和经济结构调整，煤炭等大宗物资需求下降，导致2015年一年陕西省铁路货运量出现大幅下降，铁路货运量出现了负增长，但到2016年铁路货运量又回归正常的增长趋势。由于2015年、2016年货运量数据波动较大，因此用GM（1，1）模型预测精度较差。通过改进原始数据序列光滑度，用等维新信息模型建模预测增强了前后数据关联度，弱化了原数据变动对预测结果的影响。对比两种模型的预测结果以及其与实际值的残差分析，可见改进的等维新息灰色模型预测比GM（1，1）模型预测更接近实际值，预测效果更好，见表2所列。

2.4 等维新息模型检验

后验差检验是用后验差比和小概率误差进行检验的一种模型检验方法。后验差之比记为：

（5）

式中，S12为实际数据的方差：

（6）

S22为残差方差：

（7）

残差：

（8）

小概率误差为：

（9）

小概率误差P值大说明残差与残差平均值之差小于给定值0.674 5的点的多，所以P值越接近1越好。C表示实际数据经过模型处理后所得的数据与实际值相差的大小，C越小越好。对等维新息模型预测值进行后验差检验，计算出后验差比C=0.361 5，小概率误差P=0.854 7。

3 结 语

（1）用上述建立的等维新息灰色模型对2019—2021年陕西省铁路货运量进行预测，预测结果是未来三年陕西省铁路货运量分别为：4.287 3×104万吨，4.415 4×104万吨和4.672 3×104万吨。由于2019年数据没有公布，所以模型预测的精度还需要进一步验证。

（2）将灰色模型应用在陕西省铁路货运量预测中可见GM（1，1）模型对数据有波动的问题预测效果不好，修正序列光滑度的等维新息灰色模型比GM（1，1）模型的預测精度更高，预测数据更接近陕西省铁路货运量的实际值，改进的灰色模型使GM（1，1）模型的预测值得到修正。

参考文献

[1]刘思峰，杨英杰，吴利丰.灰色系统理论及其应用[M].北京：科学出版社，2014.

[2]张军.灰色预测模型的改进及其应用[D].西安：西安理工大学，2008.

[3]朱必勇.改进GM（1，1）模型在我国石油消费量预测中的应用[J].现代矿业，2010（3）：84-87.

[4]刘玲.灰色预测模型在国内物流货运量预测中的应用[J].物流科技，2017（4）：18-20.

[5]孟庆和，谭德荣.区域物流规模发展预测方法研究[J].农业装备与车辆工程，2006（12）：15-17.

[6]杨波，吴涵.基于组合预测模型的物流园区物流需求预测：以重庆空港物流园为例[J].数学的实践与认识，2015（10）：16-25.

[7]丛苏莉.基于灰色理论和神经网络的房地产前期价格预测研究[J].现代电子技术，2017，40（11）：107-110.

[8]冯兴来，王俊，刘文兵，等.GM（1，1）的优化及在人均生活能源消费量的应用研究[J].现代电子技术，2017，40（19）：109-111.

[9]米利波.基于改进灰色模型预测的节流流量传感器测量校正方法[J].现代电子技术，2019，42（5）：180-182.

[10]曹文阳，钟志峰，李辉，等.BP神经网络在我国饲料总产量预测中的应用[J].物联网技术，2017，7（1）：96-97.

作者简介：马 睿（1979—），女，陕西咸阳人，硕士，研究方向为物流管理。