经济增长与工业环境污染关系的环境库兹涅茨曲线检验——基于长江经济带省域的面板计量模型

周正柱，刘庆波，王云云

(上海应用技术大学 经济与管理学院，上海 201418)

近年来，包括上海、江苏、浙江、安徽、重庆、云南等11个省市的长江经济带区域经济取得快速增长，但环境污染尤其工业环境污染程度也呈扩大趋势。根据《中国环境统计年鉴》计算，2016年长江经济带区域工业固体废弃物产生量约9.14亿吨，较2012年增长5.7%；工业废气排放量约368 971.7亿标立方米，较2012年增长63.7%。由此可见，长江经济带区域经济增长的同时环境污染问题不容乐观。为此，习近平总书记在党的十九大报告中明确指出要“以共抓大保护、不搞大开发为导向推动长江经济带发展”；2018年4月，习近平总书记在深入推动长江经济带发展座谈会上再次指出，生态环境保护与经济协调发展对于新形势下推动长江经济带发展具有重要意义。因此，有必要研究长江经济带区域经济发展与环境污染间的关系及其长期演变趋势，以期促进区域经济与环境的健康可持续发展。

一、 文献综述

长期以来，关于经济发展与环境保护间的关系存在着不同观点。早在20世纪70年代，“罗马俱乐部”提出了“增长极限”的观点[1]，他们认为在自然资源约束条件下，经济增长是不可持续的，为了保护环境，应该降低经济增长速度。而Dasgupta等见证了经济增长与环境改善间的良性互动关系[2]。世界发展报告(1992)也提出了类似的观点，即经济增长产生的环境问题可以用增长的经济来治理。这些成果成为20世纪90年代该领域研究转向环境库兹涅茨曲线(EKC)检验的基础。

Grossman等提出环境库兹涅茨假说来描述经济发展与环境质量间的关系，认为经济发展与环境质量间存在倒“U”型关系，这意味着环境质量水平随着经济的发展呈现先上升后下降的趋势[3]。自此以后，学者们对不同国家和地区进行了实证检验[4-5]，并扩大和延伸了假设，形成不同类型的环境库兹涅茨曲线(EKC)假设检验和研究结论。一方面，部分学者研究表明环境污染与经济发展间确实存在倒“U”型关系，如马骏等选取长江经济带9省2市2003—2014年的面板数据，利用熵值法进行实证分析，发现从污染综合水平来看，长江经济带整体经济增长与环境质量之间呈倒“U”型关系[6]。柯文岚等利用山西省1990—2009年数据模拟环境库兹涅茨曲线，发现山西EKC曲线基本存在，呈倒“U”型[7]。由此表明在一个国家的早期发展阶段,经济发展将会增加环境污染，直到该国的经济发展达到一定点时(当更多的技术可以提高能源的有效利用率)，经济发展与环境污染间的关系才呈现反向关系。另一方面，也有学者研究表明环境污染物与经济发展间不存在倒“U”型关系，而呈现多种形态。一是正“U”型，如李佳佳等检验表明，我国中部地区EKC曲线呈现正“U”型[8]；二是倒“N”型，如高广阔等以2001—2013年我国30个新型城市面板数据为例，对人均碳排放量和人均GDP的关系进行EKC检验，结果表明我国新型城市的碳排放与经济增长存在倒“N”的曲线关系[9]；三是线性等多种形态，如刘华军等以我国160个地级及以上城市作为研究样本，以PM 2.5和PM 10作为雾霾污染的衡量指标，构建空间Tobit模型对EKC假说进行检验，研究发现雾霾污染与经济发展间呈现线性递减关系[10]。表1总结了国内部分学者关于环境污染物以人均工业固体废弃物产生量、人均工业废气排放量和人均工业废水排放量为对象的EKC曲线估计结果。

表1 环境库兹涅茨曲线经验研究的EKC曲线估计结果

注：①组的两个解是基于LSDV的估计与空间相关性检验结果；②组的两个解是基于SEM估计结果；③组只有一个拐点的倒N形，还有一个关键点21 807元/人；④实证分析得出人均工业固体废弃物产生量、人均工业废气排放量与人均GDP都呈同方向发展；⑤是运用非参数估计得到的结论；⑥是运用参数估计得到的结论。

综上所述，环境污染与经济发展间呈现倒“U”型、正“U”型、倒“N”型等多种关系，即使是同一种污染物指标，EKC曲线形态也不尽相同。研究结论的不一致表明，一方面，经济发展与环境污染间的关系不存在适合所有区域的单一关系；另一方面，指标数据的选择及研究方法不同，或者现有研究往往仅考虑经济发展这一因素对环境污染的影响。EKC估计要求数据能覆盖曲线的上升部分和下降部分，而多数时间序列数据由于样本较小很难同时满足这一要求，发达国家或地区的数据往往只覆盖曲线下降部分，发展中国家或地区的数据往往只能覆盖曲线上升部分。此外，影响环境污染的因素除了经济发展外，还有区域产业结构变迁、人口迁移等重要因素。

因此，论文将利用长江经济带2004—2017年11个省市的面板数据，运用面板计量方法和参数估计模型分析长江经济带区域EKC曲线的形态和拐点问题。考虑到长江经济带各省市既包括上海、江苏和浙江东部发达省市，又包括安徽、江西、重庆、贵州、云南等中西部省市，运用11个省市面板数据能较好地克服上述缺陷。同时，考虑到参数估计可以得到变量间的数量关系并可以进行预测，这也是目前多数学者研究这一问题时常采用的方法。此外，论文在考虑经济发展这一因素时，也将城镇化、产业结构等因素作为控制变量纳入方程，进一步分析它们对研究结论的影响。

二、 变量选取、数据来源与研究方法

1. 变量选取与数据来源

为了反映经济发展与环境污染间的关系，论文借鉴学者们常采用的工业“三废”指标来反映环境污染[12,14]，同时考虑到人口规模的差异采用人均指标。经济发展指标，主要采用人均GDP指标来表示。根据经济发展对环境的影响包括结构效应、技术效应和规模效应[3]，论文也将考虑这些因素对工业环境污染的影响，其中结构效应用第二产业占GDP比重表示，技术效应用单位生产总值能耗和专利授权数表示，规模效应则仍用人均GDP表示。同时，随着国家城镇化进程的不断推进，大量人口由农村迁移到城市，必将对环境产生重要影响，论文用城镇人口占总人口比重表示，各指标、单位与符号说明如表2所示。

表2 各指标、单位与符号说明

论文实证分析采用的数据主要来源于2005—2018年《中国统计年鉴》及各省市统计年鉴，收集的主要是2004—2017年相关指标数据，其中单位生产总值能耗为能源消耗量除以GDP。

2. 研究方法

EKC曲线假说检验时常用的简化模型[3]为

(1)

其中，yit为环境变量，xit为人均收入变量，zit为影响环境的其他因素变量构成的一个向量，εit是随机误差项，β1、β2、β3和β4是估计系数。

论文主要研究经济发展与工业环境污染间的关系，同时也考虑经济发展对环境的规模效应、技术效应和结构效应，以及城镇化进程的影响。参考上述模型，同时假设各省市经济发展与工业环境污染间的曲线形态相同，但省市间存在差异。因此，采用变截距面板计量模型，模型(2)仅考虑人均GDP变量对工业环境污染的影响；模型(3)是在模型(2)的基础上增加了城镇人口占总人口比重、第二产业占GDP比重、专利授权数和单位生产总值能耗等控制变量。

yit=α+β1pgdpit+β2(pgdpit)2+β3(pgdpit)3+λ1D1+λ2D2+…+λ11D11+εit

(2)

yit=α+β1pgdpit+β2(pgdpit)2+β3(pgdpit)3+β4urpit+β5sesit+β6patit+β7penit+λ1D1+λ2D2+…+λ11D11+εit

(3)

其中，yit为环境变量，分别表示pisit、pigit和piwit，即第i省市第t年的人均工业固体废弃物产生量、人均工业废气排放量和人均工业废水排放量，pgdpit、urpit、sesit、patit和penit分别表示第i省市第t年的人均GDP、城镇人口占总人口比重、第二产业占GDP比重、专利授权数和单位生产总值能耗；β1，β2，…，β7，λ1，λ2，…，λ11都是估计系数；εit是随机误差项；i=1,2,3,…,11,代表长江经济带区域11个省市；t=1,2,3,…,14，代表长江经济带区域2004—2017年的时间段；若属于i个个体，则Di=1，否则Di=0。

三、 研究结果与分析

1. 面板数据单位根检验与回归结果

面板数据回归分析前，往往需要对数据平稳性进行检验，主要包括同质面板单位根检验(使用Levin, Lin & Chu检验)和异质面板单位根检验(使用IPS、ADF-Fisher和PP-Fisher检验)，检验结果如表3所示。由此可知，各变量均在5%水平下显著，表明各变量水平值都是平稳的，可以直接进行回归分析，回归结果如表4所示。

由表4中各污染物回归系数检验结果可知，城镇化、规模效应控制变量在5%水平下显著，技术创新效应在10%水平下显著，而结构效应并不显著。由此表明，长江经济带各省市经济增长主要通过城镇化、规模效应和技术创新效应等控制变量显著影响着工业“三废”排放量，而结构效应影响并不明显。此外，对于不同的工业污染物指标，估计得到的EKC曲线形态和转折点也有所不同；增加控制变量并不影响曲线形态，而只是提高或降低人均GDP转折点。

(1)人均工业固体废弃物产生量、人均工业废水排放量在城镇化、规模效应和技术创新效应等控制变量影响下，安徽、江西、湖北、湖南、四川、贵州、云南等中西部省市2017年人均GDP已位于第一转折点和第二转折点间(其中人均工业固体废弃物产生量由低于第一转折点转变为位于第一转折点和第二转折点间)，呈现经济增长与工业固体废弃物产生量良性发展阶段；而上海、江苏和浙江等东部省市人均GDP已超过第二转折点(其中浙江2018年人均GDP已超过第二转折点)，呈现经济增长与工业固体废弃物产生量恶性发展阶段。

(2)人均工业废气排放量尽管也受到城镇化、规模效应和技术创新效应等控制变量显著影响，但安徽、江西、湖北、湖南、四川、贵州、云南、重庆等中西部省市2017年人均GDP仍位于倒“U”型曲线转折点的左边，呈现经济增长与工业废气排放量恶性发展阶段；而上海、江苏和浙江等东部省市人均GDP已超过倒“U”型曲线转折点，呈现经济增长与工业废气排放量良性发展阶段。

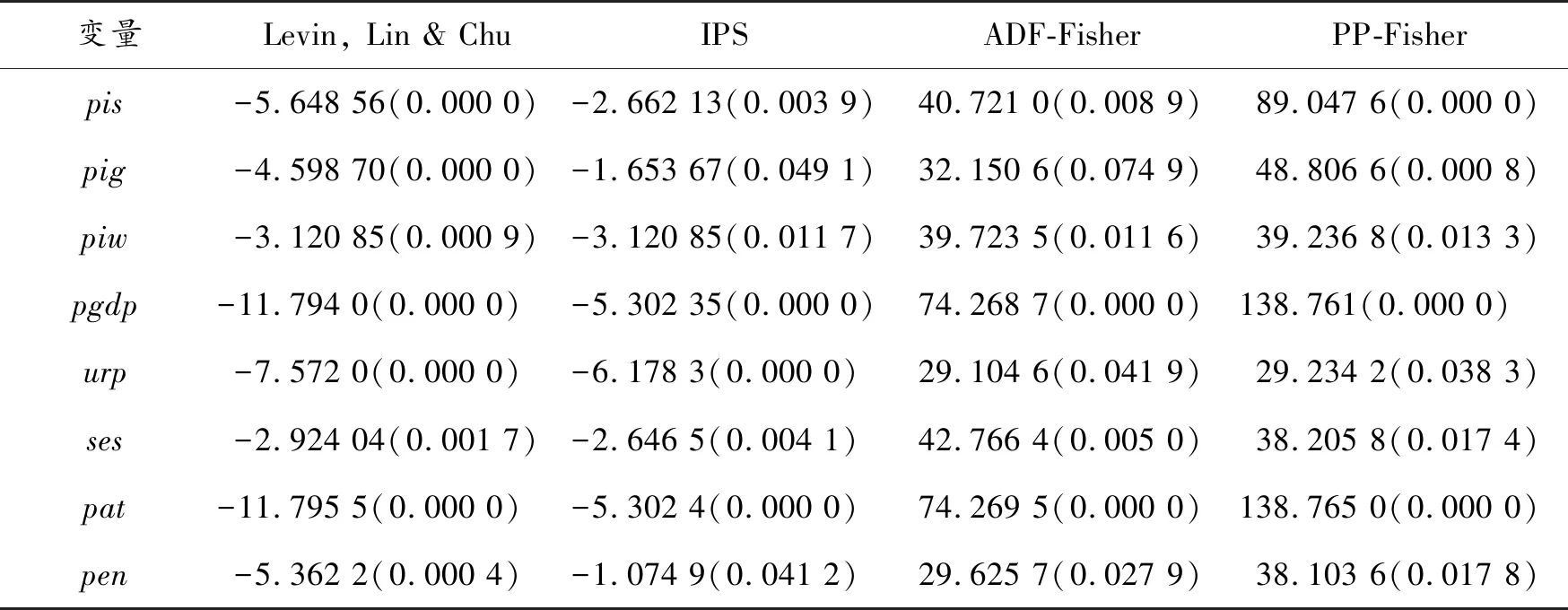
表3 面板数据水平方程单位根检验结果

注：估计方程含截距项；括号外的数字为检验值，括号内的数字为P值。

表4 三种污染物与各变量回归结果

续表

注：笔者采用Hausman检验法，运用个体固定效应模型，检验结果显著。

2. 人均工业固体废弃物产生量与人均GDP的EKC检验

图1是人均工业固体废弃物产生量与人均GDP间的曲线关系。由此可知，人均工业固体废弃物产生量与人均GDP间呈“N”型曲线关系，不含控制变量的个体固定效应模型的回归结果为

pisit=0.093 305+(7.49E-05)pgdpit-(1.07E-09)(pgdpit)2+(4.75E-15)(pgdpit)3+εit

(4)

由(4)式的估计结果可进一步计算出人均工业固体废弃物产生量与人均GDP呈“N”型曲线的转折点位于人均GDP 5.554万元和9.463万元的临界值处。这一估计结果的经济意义是：当人均GDP低于5.554万元时，该省市人均工业固体废弃物产生量将随着人均GDP的上升而增加；当人均GDP超过了5.554万元的转折点时，人均GDP继续增长将有利于降低人均工业固体废弃物产生量排放；当人均GDP突破了9.463万元后，人均工业固体废弃物产生量又将随着人均GDP的增加而上升。

当模型中增加城镇人口占总人口比重、第二产业占GDP比重、专利授权数、单位生产总值能耗控制变量时，回归曲线仍呈“N”型，只不过人均GDP两个转折点分别变为2.893万元与9.560万元。

从2017年各省市人均GDP与人均工业固体废弃物产生量的转折点来看，首先，无论模型中有控制变量还是没有控制变量，上海和江苏的人均GDP都超过了第二转折点，表明人均工业固体废弃物产生量随着人均GDP的增长呈现增大趋势；浙江与重庆的人均GDP都处于第一、第二转折点间，表明人均工业固体废弃物产生量将随着人均GDP的发展而呈现降低趋势，但浙江的人均GDP已接近第二转折点。其次，当模型中有控制变量时，其他省市呈现出明显的差异。其中，模型中没有控制变量时，安徽、江西、湖北、湖南、四川、贵州以及云南的人均GDP没有达到第一转折点，表明人均工业固体废弃物产生量将随着人均GDP的发展呈现增大趋势；模型中有控制变量时，这些省份的人均GDP处于第一、第二转折点间，表明人均工业固体废弃物产生量将随着人均GDP的发展而呈现降低趋势。

3. 人均工业废气排放量与人均GDP的EKC检验

图2是人均工业废气排放量与人均GDP间的曲线关系。由此可知，人均工业废气排放量与人均GDP之间存在显著的库兹涅茨倒“U”型曲线关系，个体固定效应模型回归结果为

pigit=0.044 004+0.000 138pgdpit-(7.81E-10)(pgdpit)2+εit

(5)

由(5)式可计算出，人均工业废气排放量与人均GDP呈倒“U”型曲线的转折点，位于人均GDP 8.835万元的临界值处。其经济意义是：随着人均GDP上升，人均工业废气排放量增加。一旦人均GDP突破了8.835万元的临界水平，该省市人均工业废气排放量才会有所减少。当模型中增加控制变量时，此时回归曲线仍呈倒“U”型，只不过转折点变为人均GDP 6.913万元。

通过对2017年各省市人均GDP值与倒“U”型曲线拐点的比较，可以看出，无论模型中有无控制变量，安徽、江西、湖北、湖南、重庆、四川、贵州、云南的人均GDP都没有达到转折点，表明人均工业废气排放量将随着人均GDP的发展而呈现增大趋势；而上海、江苏和浙江的人均GDP已超过转折点，表明人均工业废气排放量将随着人均GDP的发展而呈现降低趋势。

4. 人均工业废水排放量与人均GDP的EKC检验

图3是人均工业废水排放量与人均GDP间的曲线关系。由此可知，人均工业废水排放量与人均GDP间呈“N”型曲线关系，个体固定效应模型回归结果为

piwit=20.652 46+(7.06E-05)pgdpit-(3.43E-09)(pgdpit)2+(2.23E-14)(pgdpit)3+εit

(6)

由(6)式的估计结果可进一步计算出人均工业废水排放量与人均GDP呈“N”型曲线的转折点位于人均GDP 1.161万元和9.094万元的临界值处。这一估计结果的经济意义是：当人均GDP低于1.161万元时，该省市人均工业废水排放量将随着人均GDP的上升而增加；当人均GDP超过了1.161万元的转折点时，人均GDP继续增长将有利于降低人均工业废水排放量；当人均GDP突破9.094万元后，人均工业废水排放量又将随着人均GDP的增加而上升。当模型中增加控制变量时，此时回归曲线仍呈现“N”型，只不过两个转折点变为人均GDP 2.900万元与7.839万元。

通过2017年各省市人均GDP值与“N”型曲线拐点的比较，可以看出，模型中无论有无控制变量，安徽、江西、湖北、湖南、重庆、四川、贵州、云南人均GDP均处于第一、第二转折点间，表明人均工业废水排放量将随着人均GDP的发展而呈现降低趋势；上海、江苏和浙江人均GDP都超过了第二转折点，表明人均工业废水排放量将随着人均GDP的发展而呈现增大趋势。

根据各省市人均GDP的截面数据，运用移动平均法可以预测各省市人均GDP达到转折点对应的年份，结果如表5所示。

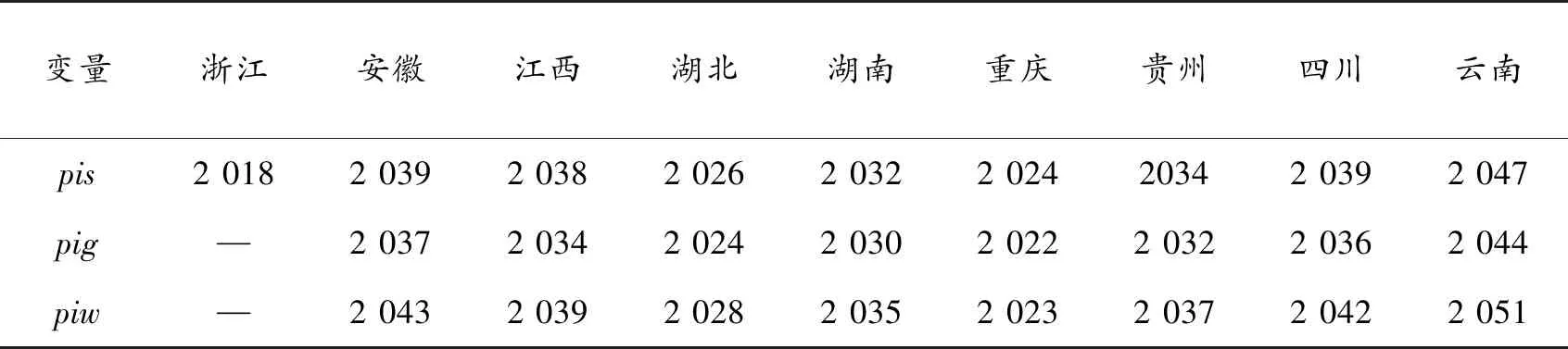
表5 各省市转折点对应年份预测

注：① 呈N型的，特指没有控制变量情况下达到第二转折点时对应的年份；② 上海、江苏的这三项指标目前已经超过第二转折点。

四、 结论与讨论

本文运用面板数据模型，检验长江经济带2004—2017年的工业“三废”与人均GDP的环境库茨涅兹曲线，结果表明：长江经济带区域人均工业废气排放量与人均GDP呈倒“U”型曲线关系；人均工业固体废弃物产生量、人均工业废水排放量与人均GDP呈“N”型曲线关系；增加控制变量并不影响曲线形态，只是提高或降低人均GDP转折点；经济增长与工业环境污染的关系在长江经济带不同区域省市存在显著差异。与其他文献的比较可知，对不同区域而言，EKC假说实质上具有不确定性。

基于上述结论，笔者认为，针对不同工业污染物，长江经济带东部和中西部省市要制定差异化政策，以期实现经济增长与工业污染物排放降低的双重目标。目前中西部省市更应关注城镇化发展和技术创新能力提升对经济发展的推动作用，从而有利于工业固体废弃物产生量和工业废水排放量的降低。但是，随着经济的快速发展，人均工业废气排放量会越来越高，更要加强与工业废气排放相关的技术改造，从而改善经济增长与其发展的不良局面。上海等东部省市目前由于城镇化率已较高，城镇化发展更应注重城镇化质量提升，同时注重与工业固体废弃物、工业废水排放相关的环保排污技术改造和技术能力提升，从而缓解经济增长与其发展的矛盾。

此外，经济增长与工业环境污染物排放的关系在长江经济带不同省市存在一定程度的差异性。长江经济带东部省市的EKC曲线转折点到来的时间总体上比中西部省市早。这种时间上的差距，本质上反映了长江经济带不同区域间的发展不平衡。其中以上海、江苏和浙江为代表的东部区域发展较快，从发展初期的高能耗高污染的产业结构逐渐转变为低能耗低污染的产业结构，第三产业占GDP比重较高；而长江经济带中西部区域则仍然以资源开采、高污染的重化工业为主的第二产业占GDP比重较高，这种产业结构分布就会造成长江经济带东部区域总体上比中西部区域的EKC转折点更早到来。因此，中西部区域需要在经济发展模式和经济激励政策上做出相应的调整，注重推进技术进步降低万元GDP能耗，同时逐步加强环境保护的立法和执法，执行更为严格的排放标准。一方面，各级政府要明确在环境保护方面的责任，充分发挥政府环境责任对企业的约束、监管作用，构建严格的企业发展环境考核标准以及经济发展的综合评价体系。另一方面，企业要树立可持续发展理念，坚持绿色发展，不断提高自主创新能力，尤其是环境保护方面的技术创新，利用先进技术解决环境污染问题。同时，深入贯彻落实新时代生态文明建设指导思想，积极推动长江经济带区域绿色和高质量发展。