一种联系数表达的位置不确定数据流聚类算法
史玲娟,黄德才
(浙江工业大学 计算机科学与技术学院,杭州 310023)
1 引 言
随着信息技术的快速发展,数据流模型在互联网数据传输、大型零售业销售信息、无线传感器网络[1,2]等众多领域中得到应用,并产生了大量不确定数据流.数据的不确定性主要由测量仪器误差、外部干扰、数据丢失、数据集成等内在和外在因素造成数据不可靠、随机、模糊、不完整等特性.
不确定数据流中的不确定数据模型一般可分为元组级(或存在级)不确定性(TLU)模型和属性级不确定性(ALU)模型.TLU描述了不确定元组存在的可能性概率,而不确定元组的属性值是确定性的.因此,仅将表示元组存在概率的概率维度加入到TLU的元组模型中.属性值的不确定性可以用ALU模型来描述[3],已有的ALU模型通常有两种形式:一种是在ALU模型中加入属性值不确定性的分布函数,另一种是加入区间数(或者由区间数衍生而来的三角模糊数和梯形模糊数)表示的属性值不确定性.位置不确定数据属于属性级不确定性的研究范畴,但它是一种新的不确定数据类型,无法用已有的ALU模型准确描述,因此需要研究新的模型来对其进行合理描述.
不确定数据流聚类算法是一个重要的研究课题,在学术界引起了众多研究者的关注.最近有大量的数据流聚类研究项目,这些研究项目产生了许多成功的算法[4].
针对存在级不确定数据流聚类问题,戴东波等[5]提出了P-Stream算法,基于不确定数据期望设置微簇核心,引入了强簇、过渡簇和弱簇的概念构造“当前簇”和“候选簇”两层簇窗口,但其离群点的处理机制不够完善,当大量离群点涌入时,离群点形成的“候选簇”会直接替代“当前簇”,从而影响最终的聚类质量;张晨等[6]提出了Emicro算法,该方法采用概率表示元组存在级的不确定性,考虑了元组间的距离和元组的不确定性,利用微簇结构存储簇的统计信息,采用“核心微簇”缓冲区和“离群点微簇”缓冲区两层聚类模型,但其离群点处理机制不够完善,当出现新的“离群点”时,采取立即将其删除的策略会误将代表新数据模型的初始数据删除,从而影响聚类的质量.Li等[7]提出了C_UStream算法,假定数据的存在概率已知,使用网格算法和滑动窗口机制,然而网格划分在处理高维数据会形成网格数据爆炸式增长,滑动窗口机制则忽略了历史数据的影响.夏聪等[8]提出了基于近邻传播的演化数据流EAP-UStream算法,该算法假定数据在每个维度上有不同的存在概率并且此概率已知,提出不确定微簇关联度的概念,并以此为基础构造不确定相似度矩阵,结合近邻传播思想实现不确定数据流演化聚类.离线聚类过程先在每个维度上进行聚类,而后进行聚类融合.郑祺等[9]提出了基于引力相似度的Gmicro算法,该算法假定数据存在概率已知,在距离度量时综合考虑元组之间的相似度与元组自身的不确定性,利用引力相似度为每个不断到达的数据元组寻找可能归属的微簇.以上算法需要以数据存在概率已知为条件,且以上算法中的存在不确定性是不确定数据的固有属性,不随时间变化.针对流数据的特征,本文采用时间衰减的存在不确定性模型,即数据的存在级不确定性随着时间增长逐渐降低.
针对属性级不确定数据流聚类问题,Aggarwal等提出了不确定数据流聚类算法UMicro[10],该算法采用标准差表示不确定性信息,构建了不确定数据聚类模型,将确定数据下的聚类特征CF结构扩展为ECF结构,但是其聚类模型更新策略易导致错误的聚类结果.其后,Aggarwal等又针对高维数据提出UPStreams[11]算法,该算法通过映射实现数据降维.Zhang等[12]提出LuMicro算法,通过使用信息熵概念度量元组的不确定属性,并将其定义不确定度,聚类的目标函数转化为整体不确定度最低.罗清华等[13]提出UIDMicro算法,采用区间数方式表示不确定数据,实现多维不确定数据流聚类.算法在计算区间数的期望距离时复杂度较高,微簇半径按照微簇中数据距离微簇中心点的期望来定义,对于新建的微簇,微簇中仅仅存在一个点或者少量数据点,微簇半径的值受初始数据点影响大,进而影响了实验结果.韩东红等[14]提出滑动窗口下基于密度的不确定数据流聚类算法USDENCLUE算法,定义了元组不确定指数和不确定度,通过寻找密度吸引点获得微簇.另外韩东红等[15]提出了一种同时考虑存在级和属性级不确定的数据流处理方法,算法要求先在半监督学习下获得聚类后的簇特征,而后在线进行分类.不适合演化性较强的数据流.
本文研究的属性位置不确定数据是属性级不确定数据中的一种,它区别于传统的属性级不确定数据,更加强调位置数据的空间关系.属性位置不确定数据广泛地存在于GIS(地理信息系统)中[16].以上属性级不确定数据流聚类算法在不确定数据相似度度量时,都没有考虑不确定数据的空间位置关系.其算法对于属性级不确定性的表达,大部分采取假定分布函数(高斯分布)的策略,通过数据样本计算分布函数中的参数(高斯分布的期望和方差).但是真实数据的实际分布函数是很难获得的[17].而文献[13]中区间数在处理空间位置关系时,受到区间数本身性质的影响,需要分别计算位置区间的上限和下限,由于区间数的两端确定、中间不确定的特点,宏观距离的取值需要人为设定参数.王骏等[18]率先在数据规模固定的数据集上用联系数巧妙地表示不确定数据对象,提出UCNDBSCAN算法.然而该算法中对象间距离衡量标准仅仅简单地运用了联系数态势值理论,使用距离的确定性联系分量加上二元距离联系数态势值表示不确定对象间的距离.本文专门重新定义了对象间的联系距离,并利用偏联系数的概念,求取距离的确定性联系分量在不确定层次上发展而来的程度,进而得到宏观距离公式.并针对数据流在线聚类过程,将二元距离联系数扩展为三元距离联系数,并运用三元联系数态势理论衡量不确定数据对象与不确定微簇之间的距离关系.
本文针对位置不确定数据流,提出一种联系数表达的不确定数据流聚类算法UCNStream.构造了针对位置不确定性的新属性不确定性数据表达模型,定义了不确定数据对象间的联系距离,构建了用于数据流在线处理的三元距离联系数下不确定对象与微簇间距离位置的衡量标准,并运用衰减函数对数据的存在不确定度进行时间衰减.算法采用在线/离线两级处理框架,在线阶段使用潜在核心微簇缓冲区(BUFc)和离群微簇缓冲区(BUFo)构成的双缓冲区,利用微簇的存在不确定度,实现新的动态调整微簇策略(离群微簇存在不确定度到达一定阈值时成长为潜在核心微簇;微簇存在不确定度过低时说明微簇过期,进行删除).离线阶段,根据密度可达等概念进行聚类,可以发现任意形状的簇.文章分析了算法的计算复杂性为线性复杂性,通过在实际数据集上与UMicro算法和UIDMicro算法的对比实验分析,实验结果表明,UCNStream算法的聚类结果在聚类纯度方面优于已有的算法,具有较好的聚类精度.
2 相关定义
本部分对本文所提出的算法中所用到的一些概念进行定义.
2.1 联系数相关定义
本文针对属性位置不确定数据,提出一种联系数表达的不确定数据表达方式.联系数是集对分析SPA[19]这一新的软计算方法中的重要概念之一,是处理数据不确定性的一种新的数学工具,在调度评估问题、聚类问题和人工智能领域[20]都有着越来越多的应用.在位置不确定数据研究中,不确定对象宏观位置的确定性和微观上不确定对象样本点位置的不确定性与集对分析理论契合.联系数在属性位置不确定数据的表达上具有优势[20],首先,联系数是中间确定两端不确定的不确定数据模型,即联系数是数据期望确定的,更符合位置不确定数据的特点;其次,联系数中不确定分量可以大于确定分量也能够小于确定分量,在位置关系的表达上有更高的一致性;最后,联系数除了两端不确定之外,还有i的不确定信息,有更丰富的关于不确定的信息.
定义1.联系数[18].称形如式(1)的数为二元联系数.
u=a+bi
(1)
其中a称为确定性联系分量,b称为不确定性联系分量,a为实数,b为非负实数,(a,b)统称为联系数u的联系分量,i∈[-1,1].
称形如式(2)的数为三元联系数,三元联系数是联系数的一般表达形式.
u=a+bi+cj
(2)
其中a称为同联系分量,b称为异联系分量,c称为反联系分量,a,b,c均为非负实数,i表示相异关系,j表示相反关系.
二元联系数u=a+bi可以看作是当a+b+c=n(n为已知常数)且a,b,c均为非负实数时u=a+bi+cj的等价表达.
定义2.二元联系数的四则运算[18].
1)二元联系数加法运算
设u1=a1+b1i,u2=a2+b2i是两个二元联系数,则:
u1+u2≜(a1+a2)+(b1+b2)i
(3)
因为a1,a2是实数,所以(a1+a2)是实数.又因为b1,b2是非负数,所以(b1+b2)是非负数.因此,二元联系数相加的结果依然是一个二元联系数.
2)二元联系数减法运算
设u1=a1+b1i,u2=a2+b2i是两个二元联系数,则:
u1-u2≜(a1-a2)+(b1+b2)i
(4)
易证,二元联系数相减的结果依然是一个二元联系数.
3)二元联系数乘法运算
设u1=a1+b1i,u2=a2+b2i是两个二元联系数,则:
u1*u2≜(a1*a2)+(b1*b2)i
(5)
易证,二元联系数相乘的结果依然是一个二元联系数.
4)二元联系数根式运算
设u=a+bi是一个二元联系数且a非负,则:
(6)
易证,二元联系数相乘的结果依然是一个二元联系数.
定义3.联系数的态势[21].
态势是指联系数中各联系份量大小关系所确定的系统状态和趋势.不同联系数中联系分量的大小关系规律可以用联系数的态势函数来描述.
1)二元联系数的态势
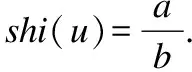
表1 u=a+bi的态势函数表
Table 1 Situation function table of u=a+bi

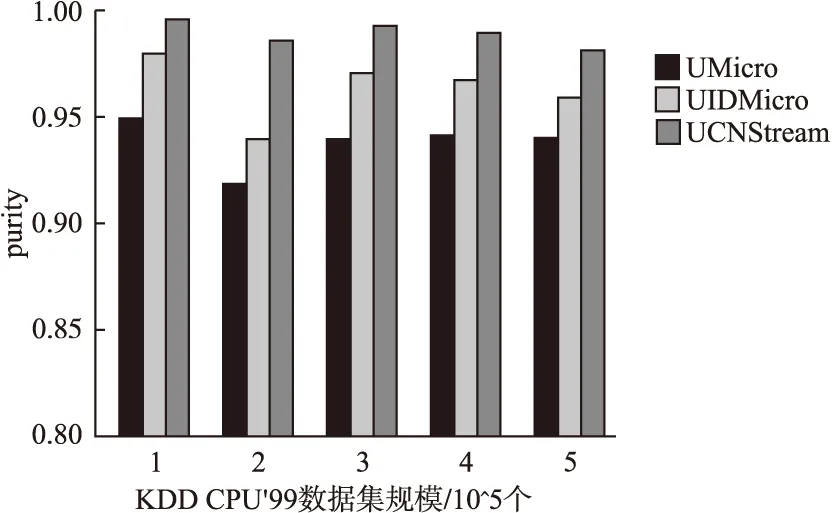
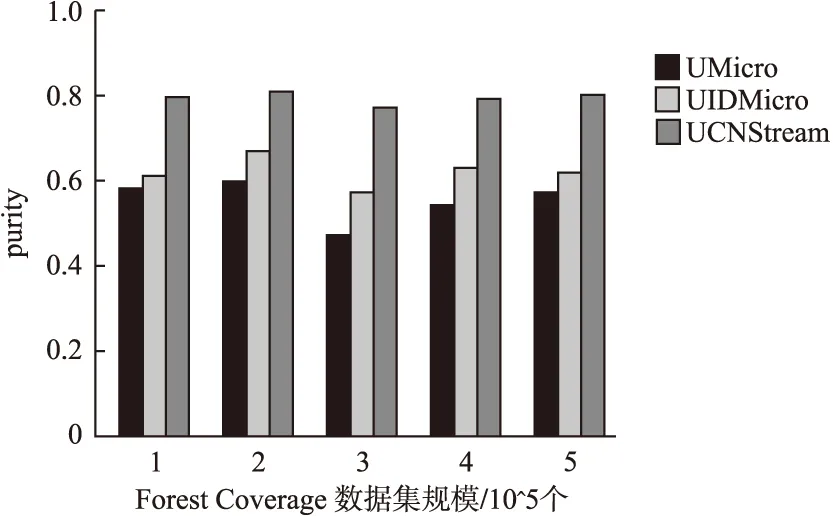
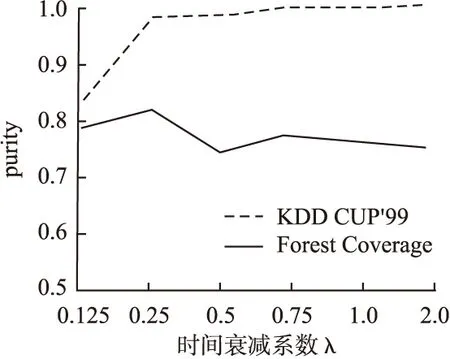
联系分量的大小关系态势态势函数shi(u)=aba>b同势>1a=b均势=1a 2)三元联系数的态势 若联系数的态势大于1,即a>c,则属于同势,同势的情况下,b的值越小,同势的等级越高. 若联系数的态势等于1,即a=c,则属于均势,均势的情况下,b的值越小,均势的等级越高. 若联系数的态势小于1,即a 如果用三元联系数表示距离,那么同势的情况表示距离倾向于更大的方向,且同势时相同态势值的联系数,同势等级越高,宏观上距离越大;同理,反势的情况表示距离倾向于更小的方向,且反势时相同态势值的联系数,同势等级越高,宏观上距离越小;在均势的情况下,表示距离倾向于中立,且均势时相同态势值的联系数,均势等级越高,宏观上这种中立的倾向越大. 定义4.二元联系数的偏联系数[21].设u=a+bi是一个二元联系数,则有: 偏同联系数∂+u: (7) 偏反联系数∂-u: (8) 全偏联系数∂u: (9) 全偏联系数也简称偏联系数.其中偏同联系数∂+u刻画了联系数中确定性联系分量a由原先处在b层次上正向发展而来的程度;偏反联系数∂-u刻画了联系数中不确定联系分量b由原先处在b层次上负向发展而来的程度. 定义7.不确定数据对象间的联系距离.不确定数据对象X1,X2间的联系距离表示为dis(X1,X2). dis(X1,X2)= (10) dis(X1,X2)是一个联系数,可以表示为dis(X1,X2)=udis=adis+bdisi.此时偏同联系数∂+u代表了距离确定联系分量在不确定层次上正向发展的程度,而不确定数据距离计算的时候更加注重距离最小的情况,即确定联系分量在不确定层次上反向发展的程度1-∂+u.进而,可以得到确定联系分量在不确定层次上反向发展的距离adis′=adis*(1-∂+u).本文用确定联系分量减去确定联系分量在不确定层次上反向发展的距离表示X1,X2的宏观距离Dis(X1,X2). (11) 由定义7可以得到结论1: 定义8.时间衰减.随着不确定数据流的演化,每个数据对象的存在不确定度随时间增长呈现衰减趋势,本文假定数据对象的存在不确定度初始值为1,使用时间衰减函数D(x,t)=2-λ(t-T(x)),衰减系数λ∈(0,1),λ越大衰减程度越高. 由定义8可以得到结论2: 定义10.不确定微簇中心.不确定微簇UC的中心由微簇中心期望和微簇不确定度构成,微簇中心的期望定义为在当前微簇存在概率下的线性平均值: (12) 微簇中心的不确定度同样取一个标准差,定义为簇内各数据对象到微簇中心的期望距离平方和的均值的平方根. (13) 定义11.不确定微簇半径.微簇半径由确定部分和不确定部分综合得出.半径取簇内各数据对象到微簇中心的平均距离.根据联系数的运算法则,确定部分的值为R1,不确定部分的值为R2. (14) (15) 不确定数据对象与不确定微簇集合set(C)={C1,C2,C3,…,Cm}之间,有不确定距离集合set(dis(p,C))={dis(p,C1),dis(p,C2),…,dis(p,Cm)},存在不确定距离上界记做maxset(c),p=max(ap,cx+bp,cx).因此,距离联系数可以扩展为a+b+c=maxset(c),p的三元联系数. 不确定数据对象p与不确定微簇Cm间距离的三元联系数表示为up,cm=ap,cm+bp,cmi+cp,cmj,其中c=maxset(c),p-ap,cm-bp,cm. 不确定数据对象p与不确定微簇Cm间的距离态势GP(up,cm)=eap,cm-cp,cm,态势值越小,距离越接近. 定义13.核心微簇(core-micro-cluster).将存在不确定度大于μ的潜在核心微簇定义为核心微簇. 定义14.潜在核心微簇(potential c-micro-cluster).将存在不确定度大于βμ的微簇定义为核心微簇.参数β∈(-1,1). 定义15.离群微簇(outlier micro-cluster).将存在不确定度不大于βμ的微簇定义为核心微簇. 定义16.直接密度可达.不确定微簇UC1和UC2,其中UC1是核心微簇,UC1和UC2微簇中心的宏观距离小于2ε,则称UC1到UC2直接密度可达. 定义17.间接密度可达微簇.不确定微簇UC1和UC2,其中UC1是核心微簇,存在一条核心微簇链UC1,…,UC2,则称UC1到UC2间接密度可达. UCNStream算法主要包括初始化、在线微簇维护算法和离线宏聚类算法三个部分.初始化阶段利用初始的小规模数据集调整参数;在线部分利用不确定数据本身的特点构建和维护不确定微簇;离线阶段进行基于密度的不确定数据宏聚类.算法主要步骤如下: Step1.利用初始数据集,调整算法参数. Step2.调用在线微簇维护算法,动态调整微簇的数量和微簇聚类特征. Step3.提交聚类请求,进行宏聚类算法. 基于密度的聚类算法中,密度半径ε和密度阈值μ是两个非常重要的参数,通过对初始样本数据进行分析,将这两个参数自适应地初始化,参数初始化的部分包含两步: Step1.由于中心是局部密度较大且距离其他中心较远的点,同时满足这两个条件的点称为密度峰值,选用一个较小的截断距离,利用密度峰值算法对初识数据集进行聚类,得到合理的簇间最小联系距离,利用公式(11)计算其对应的宏观距离,初始化微簇半径ε为这个宏观距离的一半. Step2.按照ε邻域下局部密度和数据对象到其他簇中心最短距离的乘积大小,将初始数据集降序排列构成数据队列ListData. Step2.1.取出ListData中最前的一个数据点p,构建以点p为中心,半径为ε的微簇,微簇含有数据点数量n=1. Step2.2.依次取出ListData中最前的一个数据点p,直到ListData为空时转Step 2.4.如果数据点p落在已有的微簇半径范围内中,该微簇的数据点数量n增加1,重复Step 2.2.否则,转Step 2.3. Step2.3.获取数据点p到最近一个微簇的距离d,如果d≥2*ε,构建以点p为中心的微簇.否则标记这个数据点为待处理,转Step 2.2. Step2.4.依次取出ListData中标记为待处理的数据点p,如果数据点p落在已有的微簇半径范围内中,该微簇的数据点数量n增加1.否则,构建以点p为中心的微簇. Step2.5.计算微簇中包含数据的平均个数,作为μ的取值.并将微簇中含有数据点数量大于μ的微簇作为初始的潜在核心微簇. 这个初始化的过程,既得到了初始的潜在核心微簇,也达到参数初始化的目的.克服了UIDMicro算法直接将最初的nmicro个数据分别生成微簇,进行初始化当前微簇窗口的不合理性.UIDMicro算法初始化得到的微簇窗口不具备微簇的代表性,将导致聚类初期微簇结构频繁地更新,微簇边界值的判定条件无法形成.同时,参数选择上优于UIDMicro算法中给定微簇最低包含数据个数阈值的做法.初始化算法对后续的运算过程和聚类结果都有积极的意义. 在线微簇聚类算法采用双缓冲区,即潜在核心微簇缓冲区(BUFc)和离群微簇缓冲区(BUFo),BUFc中更新并保存潜在核心微簇的聚类特征;BUFo中更新并保存离群微簇的聚类特征,当一个离群微簇成长为潜在核心微簇时,将该微簇的聚类特征转存到BUFc中.令nc表示潜在核心微簇缓冲区内可保存微簇的最大值,no表示离群微簇缓冲区内可保存微簇的最大值,noc表示内存中限定的微簇数量最大值. 在线微簇维护算法分成在线聚类和在线缓冲区更新调整两个部分.在线聚类算法根据不断到达的数据对象更新微簇的聚类特征,在线缓冲区更新调整算法则定时检查微簇是否存在度过低,并删除那些存在度太低的不确定微簇. 在线聚类算法 Step1.对于每个到来的数据对象p,尝试把数据对象放入距离态势最小的潜在核心微簇.如果加入p后,微簇的宏观半径小于阈值ε,则确认p的分配,更新微簇聚类特征,转Step 1.否则,转Step 2. Step2.尝试把数据对象p放入距离态势最小的离群微簇.如果加入p后,微簇的宏观半径小于阈值ε,则确认p的分配,继续Step 2的子操作.否则,转Step 3. Step2.1.更新微簇聚类特征,如果更新微簇聚类特征后,离群微簇存在不确定度大于βμ,(说明这个离群微簇已经成长为一个潜在核心微簇),进入Step 2.2.否则,转Step 1. Step2.2.检查潜在核心微簇缓冲区是否已满,如果潜在核心微簇缓冲区已满,则删除潜在核心微簇缓冲区中存在不确定度最低的微簇. Step2.3.将这个微簇从离群微簇缓冲区转存到潜在核心微簇缓冲区.转Step 1. Step3.检查离群微簇缓冲区是否已满. Step3.1.如果离群微簇缓冲区已满,则删除离群微簇缓冲区中存在不确定度最低的微簇. Step3.2.为数据对象p建立新的离群微簇. 由上述过程可知,算法优先考虑吸收新数据对象,然后考虑创建新微簇,这样能够避免本应属于某个现有微簇的数据对象占用内存微簇存储资源和在后续聚类中进行微簇合并的多余操作,避免现有微簇因存在不确定度降低过快而过早被删除.从Step 2的子操作可发现,本文及时更新由离群微簇成长而来的潜在核心微簇进入BUFc、维护在线聚类模型,使数据对象尽可能被潜在核心微簇吸收. 根据结论2易知核心微簇密度μ与潜在核心微簇密度βμ之间应满足μ的关系,β取值应不小于1-2-λ,本文采用向上取值保留1-2-λ小数点后一位,得到潜在核心微簇最小密度参数βμ. 间隔时间Tp进行微簇的存在度检查并更新微簇,微簇删除机制算法过程如下. 在线缓冲区更新调整算法 Step1.检测潜在核心微簇. 如果存在不确定度p.w<βμ,删除这个微簇. Step2.检测离群微簇. 如果存在不确定度p.w<ξ,删除这个微簇. 本文缓冲区的更新调整策略中,首先,针对新成长的潜在核心微簇使用及时更新替换的方式;其次,针对存在不确定度过低的微簇,每隔Tp时间隔间进行检查.由于微簇模型稳定,演化率低时新成长的潜在核心微簇较少,此时及时更新替换的方式消耗资源很少;演化率高时新成长的潜在核心微簇较多,及时更新替换使后续相应的数据对象仅需在一个缓冲区进行匹配,减少计算量.而存在不确定度过低的情况不需要实时检查,周期检查已经可以达到相同的检查效果. 在离线聚类的过程中,收到聚类请求后,进行离线宏聚类.离线宏聚类使用潜在核心微簇缓冲区中的数据,根据密度可达定义进行宏聚类得到最终的聚类结果,这种方式可以在提前将离群点检测剔除的基础上处理任意形状的微簇. 宏聚类算法 Step1.取出一个未被处理的潜在核心微簇p,直到取完 Step2.如果p是核心微簇(p.w>μ),标记为已处理微簇,将与p直接密度可达的微簇加入到待处理adjacentPoints列中,以潜在核心微簇p创建簇C.否则,转回Step 1. Step3.adjacentPoints列非空时,从adjacentPoints列取出一个潜在核心微簇p,否则,转回Step 1. Step4.如果p是核心微簇(p.w>μ),标记p的归属簇为C,标记p为已处理微簇.将与p直接密度可达的微簇加入到待处理adjacentPoints列中,从adjacentPoints列移除p,转Step 3.否则,转Step 5. Step5.标记p的归属簇为C,标记p为已处理微簇.从adjacentPoints列移除p,转Step 3. UCNStream算法主要包括初始化、在线微簇维护算法和离线宏聚类算法三个部分.下面分别计算这三个部分的计算复杂度并由此进一步得到算法的整体计算复杂度. 1)初始化部分的计算复杂度分析. 设初始化阶段使用的数据量大小为常量m0.使用密度峰值算法,通过计算位置不确定数据对象两两之间的距离并与取值较小的截断距离比较,获取数据对象的局部密度、到其他微簇中心的最短距离,进而根据密度峰值单遍扫描初始化数据集得到初步的聚类结果.密度峰值算法本身的计算复杂度为O(m02). 紧接着计算簇间最小距离,初始化微簇半径ε,然后以ε作为参数重新聚类,根据聚类结果获取局部密度参数和初始的潜在核心微簇,计算复杂度分别为O(m0)和O(m02). 因此,初始化部分整体的计算复杂度为O(m02). 2)在线微簇维护部分的计算复杂度分析. 设数据流到达的数据量大小为n,微簇数量总和|C|,其中n随时间不断增长,|C|存在上限,且该上限是不随数据对象数量变化的常量.在线微簇维护过程中,包含数据对象的分配问题和间隔时间Tp执行微簇删除机制两部分. 对于数据对象的分配问题,设数据对象和已有微簇之间的距离关系计算判断数据对象如何分配所花费时间为某个常数因子c1,则有T1(n)≤|C|*n*c1=O(n). Tonline(n)=T1(n)+T2(n),因此在线微簇维护部分的计算复杂度为O(n). 3)离线宏聚类部分的计算复杂度分析. 离线宏聚类对潜在核心微簇进行聚类分析,潜在核心微簇的数量不超过常量|C|,算法需要扫描所有未处理的微簇和其直接密度可达的微簇,因此计算复杂度为O(|C|2). 4)算法整体计算复杂度分析. 算法整体的计算复杂度由上述三个部分组成,由于初始化部分的计算复杂度为O(m02),在线微簇维护部分的计算复杂度为O(n),离线宏聚类部分的计算复杂度为O(|C|2),其中m0和|C|是给定常量,因此算法的整体计算复杂度为O(n),呈现线性复杂度,符合数据流聚类算法在无限增长的数据规模下聚类效率的要求. 本实验所用的计算机内存8GB DDR3,固态硬盘256GB,CPU为2.7 GHz Intel Core i5,操作系统采用MACOS Mojave.开发环境为IntelliJ IDEA ULTIMATE2017,编程语言选择JAVA. 本实验采用数据流算法最为通用的两个真实数据集:KDD CUP′99和Forest Coverage进行实验.KDD CUP′99是一个网络入侵检测数据集,数据模型的动态演化比较明显,数据集包含近500万条传输控制协议(TCP)连接记录,每条记录对应着一次正常连接或者22种网络攻击之一,同时每条TCP连接记录中一共包括42个有效属性,从中选择34个连续属性构成实验数据;Forest Coverage数据集一共包含581012条记录,每条记录有54个数值构成的12个属性值,对应7个类,我们从中抽取10个数值型属性作为聚类实验使用,以记录的自然顺序作为数据流的输入顺序. 数据的不确定化处理方式为:对数据的每一个属性生成random[1,q]个对应的子属性值,每个子属性值的取值为原先属性值基础上加入N(0,ηδ2)的高斯白噪声. 为了更好地进行实验分析,将UCNStream算法的聚类结果与UMicro算法和UIDMirco算法的聚类结果进行比较.由于UMicro算法和UIDMirco算法不是针对位置不确定数据设计的不确定数据流算法,特将位置不确定数据映射成为以上两种算法中不确定数据的表达形式:对于UMicro算法,求取位置不确定数据对象每个维度的均值和标准差,不确定数据以均值向量和标准差向量记录,不确定数据点之间的距离不考虑空间位置关系;对于UIDMirco算法,求取位置不确定数据对象在每个维度的取值范围,不确定数据用区间数表示,不确定数据点之间的距离由区间数之间最小距离和最大距离决定. 为了避免参数选择的盲目性,实验中的相关参数设置参考文献[10]和文献[13],并结合UCNStream算法的计算结果,进行如下设置:数据流流速v=1000,噪声因子η=1,对于UCNStream算法其他参数的取值情况分别为衰减系数λ=0.25,微簇缓冲区大小nc=200,no=20;对于UMicro算法其他参数设置分别为收纳半径阈值τ=3,权重比阈值0.02,微簇窗口大小nmicro=200;对于UIDMirco算法其他参数设置分别为收纳半径阈值τ=3,包含因子κ=1,当前微簇窗口大小nmicro=200,候选微簇窗口大小为20,微簇最小密度阈值Th=4. 在对属性位置不确定数据流聚类结果评估时,由于实验中使用的所有数据集都知道真正的类标签,因此通过外部评价指标聚类的纯度(purity)来评估聚类的质量.聚类的纯度定义为: (16) 使用聚类的纯度purity作为聚类质量的评价指标,聚类的纯度越高,聚类质量越好.实验对UMicro、UIDMicro和UCNStream算法在不同数据规模下产生的处理时间进行对比,KDD CUP′99数据集上的实验结果如图1所示,Forest Coverage数据集上的实验结果如图2所示. 图1 KDD CUP′99数据集不同数据规模下算法聚类纯度比较Fig.1 Purity for different clustering algorithms with different KDD CUP′99 data size 由上述结果可知,在对位置不确定数据集进行聚类时,相对于UMicro算法和UIDMicro算法,UCNStream算法有较高的聚类纯度.在解决位置不确定数据流的聚类问题上具有优势. 图2 Forest Coverage数据集不同数据规模下算法聚类纯度比较Fig.2 Purity for different clustering algorithms with different Forest Coverage data size 4.5.1 衰减系数λ对实验结果的影响 衰减系数λ决定历史信息对当前聚类的影响程度,实验在真实数据集的基础上使用不同的衰减系数λ产生不确定数据进行聚类.实验得到的聚类纯度随衰减系数变化曲线如图3所示. 图3 聚类纯度随时间衰减系数λ变化曲线Fig.3 Purity versus decay factor λ 由图3可知,时间衰减系数对于两个数据集有不同的影响,对于网络入侵检测数据集在衰减系数大于0.75后,聚类纯度接近1,这是因为网络入侵检测数据集中大量的网络攻击连接在一定时间段连续进行,而后又呈现大量连续的正常连接数据,减小历史数据对当前聚类结果的影响能得到更好的聚类效果.而Forest Coverage数据集中,时间衰减系数增大没有使聚类的纯度提升.因此,对于KDD CUP′99数据集,衰减系数取值在0.25以上较为合适,对于Forest Coverage数据集衰减系数在0.5以内有较好的聚类效果.综合考虑,本文衰减系数取值为0.25.衰减系数的值要根据实际情况进行设定. 4.5.2 噪声因子η对实验结果的影响 噪声因子η决定数据不确定性的程度,实验在真实数据集的基础上使用不同的噪声因子产生不确定数据进行聚类.实验得到的聚类纯度随噪声因子变化曲线如图4所示. 图4 聚类纯度随噪声因子η变化曲线Fig.4 Purity versus noise factor η 由图4可知,聚类纯度随噪声因子η的增大呈逐渐降低的趋势.这是因为随着噪声因子η的增大,数据的不确定性程度变大,使得簇间相似度降低,因此,聚类纯度降低.噪声因子大于1时,对聚类纯度产生明显的影响. 针对位置不确定数据无法用现有的ALU模型描述,将位置不确定数据处理为普通的属性级不确定数据时数据对象的位置关系不能良好体现的问题,本文提出一种联系数表达的不确定数据流聚类算法UCNStream.通过实验展示和结果分析,该算法具有线性的计算复杂度,性能良好;充分利用位置不确定数据的特点,聚类精度高;实验中使用了数据集中数值属性的部分,因此下一步的工作是分析分类属性和混合属性中位置不确定数据流的聚类问题.
2.2 算法相关定义



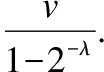
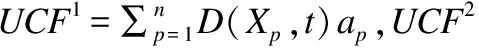
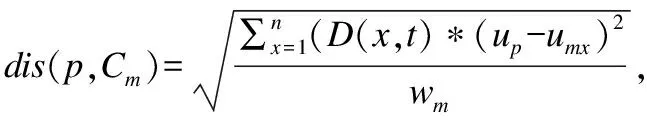
3 UCNStream算法
3.1 初始化算法
3.2 在线微簇维护算法
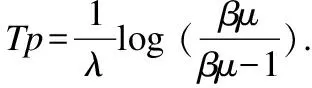
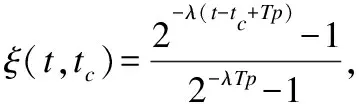
3.3 离线宏聚类算法
4 实验与分析
4.1 计算复杂度分析
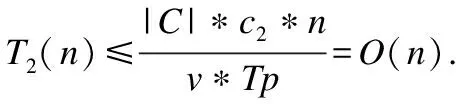
4.2 实验环境
4.3 数据集和参数设置
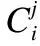
4.4 聚类质量分析
4.5 参数对聚类质量的影响

5 总 结

