基于无线传感网络收集设备最佳传输策略研究
陶忠良
(吉林化工学院 航空工程学院,吉林 吉林 132022)
随着科技的发展,无线传感网络进入我们的视野.而智能传感网络由于能够提供更好的服务,逐渐成为研究一个热点.智能传感网络设计中包括感应方式、节点处理信息的能力、传输和储存的能力.但是在实际生活中,由于电池容量有限,极大的限制了传感器节点,一旦电池没电,节点就不能正常运行,这就意味着网络需要定时更换电池,而更换电池也会带来额外的损耗.为解决电池供电的问题,提高传感器节点的使用寿命,采用能量收集技术,使得节点可以从周围环境中收集能量[1],转化为电能并储存,利用这些能量来供传感器工作.研究设计一种高效的能量传输策略,在保证节点能正常传输的同时,能够使得网络持久运行.
1 能量收集技术和均衡操作
研究的无线传感器是可充电的、能进行智能能量管理的传输节点,它具有能量收集功能.此外,为了保证网络的正常运行,节点还需要采用均衡操作,实现优化的系统性能.
1.1 能量收集技术
研究的主体对象无线传感器,就是把收集到的能量转换成电能供节点处理信息所用.能量收集技术涉及到3个要点,分别是能量源、能量收集机构和负载元件[2].
能量收集中最基础也是最重要的部分就是可收集的能量源.能量源的形式多种多样,但是可以从速率、大小等角度来衡量[3].常见的能量收集结构包括无存储收集和有存储收集两种.前者的实现简单但是局限性大,后者实现复杂但是性能良好,可以广泛使用.无存储收集结构如图1所示,此时收集到的能量直接传给了无线传感器使用.有存储收集结构如图2所示,这种方式可以智能控制能量的分配,提高能量的利用效率,该结构非常适合可预测的能量源[4],白天收集到多余的能量可以储存起来,供晚上传感器节点使用.

图1 无存储收集结构图

图2 有存储收集结构图
1.2 均衡操作
根据现有的电池能量水平和预测收集的能量,需要充分考虑能量均衡操作的问题,这样才能使其能量高效地被利用并完善系统相关性能.
要实现节点能量均衡,必须确保节点不会由于能量用尽而停止工作,同时还要保证性能的最大化.
定义Pi(k)为能量源在时隙收集能量的功率,P0(k)表示为节点用于传输任务消耗的功率.基于两种不同的系统结构,实现能量均衡的条件如下.
对于无存储系统,由于收集得到的能量立即被节点使用,可得到条件Pi(k)≥Po(k)∀k[5].这种系统结构下,会有Pi(k)-Po(k)部分的能量浪费.对于有存储的结构,这里有一个关键的元件能量存储器,系统中由于有了能量的存储,所以在有些时间段内可能不满足Pi(k)≥Po(k),但是仍然满足均衡条件,此时得到新的限制条件.假设B0为初始存储单元剩余的能量,考虑所有时隙能量的收集和消耗,得到
(1)
研究表明,当节点进行工作和切换操作时,消耗的能量比最小工作点的能量还要高,且频繁切换会对节点造成损害.均衡操作中要求系统在无传输任务时也会执行一些额外的任务.
2 能量收集传输理论和系统模型
为了得到收集设备最佳传输策略,研究建立系统模型,模型主要参数见表1.假设一个时隙系统,时隙k∈0对应于时间间隔[k,k+1)[6].考虑能量收集装置(EHDs)能从周围环境得到能量,收获的能量存储在能量缓冲区中,表示为能量量子的形式Δe[J],能量缓冲区总量为emax(量子形式)[7].
2.1 动态的电池能量
由于在时隙系统的每个时隙都收集能量也会取走能量,在某些情景下还会发生能量溢出和用尽,所以电池中的能量是在动态变化的[8].假定时刻k缓存区中的能量表示为Ek∈ε,ε≡{0,…,emax}.第k时隙的开始,EHDs控制器请求从缓冲区抽取能量量子Qk执行特定任务,Qk∈Q,Q={0}∪{qmin,qmin+1,…,qmax},其中0 Ek+1=min{[Ek-Qk]++Bk,emax},k≥0. (2) 参考表1模型的主要参数,Ek、Bk和Qk是用能量量子数表示的离散变量.由于能量量子表示为Δe[J],电池状态、收集的能量、抽取的能量可以分别表示为ΔeEk[J]、ΔeBk[J]和ΔeQk[J].但在实际中,这些物理量都是在集合中取值的连续变量.经过抽样、量化,可以将模拟量转化为数字量.这个量化引入的误差可以精确到一个的能量量子Δe.容易知道,能量量子的值越小,量化的电池容量emax、最大的收获能量bmax和最大负载要求qmax的值越大,这使得优化复杂度更高.因此,能量量子的值反映了优化复杂度与建模精度的折衷. 表1 模型的主要参数表 方程(2)揭示了能量收集过程和消耗过程两个重要的现象.前者被定义为能量用尽,对应于能量收集装置EHDs在完成要求的任务之前能量消耗完,此时Qk>Ek.这导致了任务失败和电池中可用能量的耗尽.后者是当Bk>emax-[Ek-Qk]+时能量溢出可能发生,即能量缓冲区无法存储所有收获的能源Bk,造成Bk-emax+[Ek-Qk]+能量量子的损失[9]. 把电池状态信息、传输信道信息作为不同的情景来处理,设计传输策略及系统模型来适应这些情景,从而得到比较好的性能.为了比较不同策略性能的优劣,这里定义吞吐量性能指标.当电池状态信息为Ek=e∈ε,传输信道增益Ck=c,选定Qk=q时的吞吐量性能g(q,c,e). (3) (4) 结合上面的分析,基于电池状态信息和传输信道信息的情景,定义吞吐量性能指标 (5) 研究知道传输信道服从瑞利衰落,能量收集过程虽然是随机的,但是可以从独立性和相关性两方面来描述,电池状态虽然在每个时隙都会变化,但是也可以定性的描述水平高或低.不同状态将会影响策略的设计,会对策略的性能产生较大影响. 电池状态信息、传输信道状态信息都会对性能有一定的改善,现有研究已证明,如果可以合理利用能量收集相关性并适应这个过程,也会带来性能的明显提高.在这里综合考虑这些因素,得到最优的传输策略.同时为了适应实际中传输任务多次发生的情景,还对抽取能量进行建模分析,得到了适合在实际中应用的传输策略. 3.1.1 适用于能量收集和传输的最佳传输策略 定义I(0)、I(1)分别代表电池状态信息低和高的两个间隔,Sk状态好、坏和随机情景分别决定Bk的不同的值,传输信道状态分为好、中、差3种,根据这些信息,合理地调整成功因子η的值,可以更合理地分配能量,在保证成功率的同时,使得能量高效利用[10].下面具体介绍该策略. 根据前文可知,外部环境的好坏和成功因子的大小决定了应该抽取最小能量的值,所以应该根据三者的状态选择合适的成功因子.当电池能量充足、传输信道不是很差的环境下采用尽可能大的成功因子,保证任务的成功;为了实现长期吞吐量性能的最佳,应尽量避免取尽缓存区中的能量,这会导致下一时隙性能损失较大;当外部环境很差时,特别是此时能量不足或者能量收集不理想时,可以等待保持空闲状态的下一时隙执行,这样通过时延可以在保证功率的同时提高吞吐量,把这种策略记作P4. [battery capacity emax]/[avg harv rate b]图3 P4的性能分析图 由图3可知,虽然两种策略性能有差别但是它们随着电池容量的变化具有相似性,这是因为它们都基于能量到达信息来合理分配能量.该策略综合考虑了外部信息、能量到达信息、电池状态信息,这些信息都通过估计或设备测量,所以这种方式是可行的. 在这些信息的基础上进行能量分配,得到了最理想的性能.且这种策略下,在较小的电池容量时就能接近策略的极限,所以在小电池情境下效果更为理想.通过上面的分析,在条件允许时,应采用策略P4的方式来进行传输. 3.1.2 适用于实际的最佳传输策略 前文分析的重点都是针对电池状态信息和传输信道状态信息的,对执行任务能量的模型没有过多的研究.虽然前者可以在一定程度上保证任务的成功率,但是这是一种不精确的方式.根据中心极限定理,当事件大量发生时,事件发生可以近似为正态分布,这里利用此结论来建立执行任务能量的模型,更合理地分配能量. 根据上述分析,qta·Ck=qexe,所以当外部状态好的情况(Ck>χ1=1)只要抽取qexe的能量即可;当外部状态好的情况(Ck>χ2=0.5),就需要抽取2qexe才能保证任务的成功;当外部状态不好的情况(Ck<χ2=0.5),如果此时能量充足就执行任务,如果能量不充足,就尽力而为地去执行,策略P5性能分析见图4. 由图4可知,策略P5的平均性能稳定在3.3左右,在同样已知电池状态信息和传输信道信息的情况下,这个指标比策略P4稍好,这意味这种策略的效果更为理想,由于对实际中抽取的能量进行了建模分析,不是盲目的抽取能量,策略P5更合理地分配了能量,可以使电池能量维持在一个较高的水平.由于策略P5的操作简单,能量分配合理,而且性能稳定、更适用于实际生活,是一种理想的传输策略. [battery capacity emax]/[avg harv rate b]图4 策略P5性能分析 出于实际的考虑,在电池状态信息、传输信道信息和能量收集信息部分已知的假设条件下,研究了不同情境下的传输策略.研究表明,在部分已知外部状态信息的前提下,完全已知电池状态信息只能带来很少的增益,但是相对的,要准确地估计或者测量得到这种信息代价可能很大.结果显示,相比部分已知传输信道信息的情况,完全已知电池状态信息只能带来很少的性能提高.所以策略重点在于分析部分已知状态信息的情况.通过分析可知,对这些状态信息的部分已知都比完全未知信息时的性能要提高很多.因此,对这些外部状态信息、能量到达信息、电池状态信息的部分已知对性能改善更为关键.

2.2 系统模型的建立



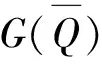
3 传输策略的性能仿真分析
3.1 基于有限电池状态信息最佳传输策略


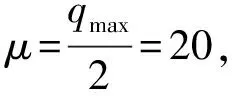


4 结 论

