基于强化学习的超启发算法求解有容量车辆路径问题
张景玲,冯勤炳,赵燕伟,刘金龙,冷龙龙
(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室,浙江 杭州 310014)
0 引言
为了有效分配物流资源,减少运输成本,车辆路径问题(Vehicle Routing Problem, VRP)一直是物流调度领域研究的热点问题。车辆路径问题最早由Dantizg等[1]于1959年提出,其基本问题为有容量车辆路径问题(Capacitated Vehicle Routing Problem, CVRP),该问题在满足车载量约束条件下,以服务所有客户的最小化车辆行驶距离为目标,达到降低物流配送成本的目的。因此,本文提出一种基于强化学习的超启发算法,致力于更有效地优化配送路径,解决车辆路径问题。
近年来,各种算法被应用于求解VRP以及衍生类问题。精确算法方面,如:分支定界法[2],最小化K-trees[3],动态规划算法[4]等,此类算法能求得全局最优解,但是当客户点规模较大时,求解时间较长;传统启发式算法方面,如:节约法[5],两阶段法[6]等,相较于精确算法,能够更加有效地找寻最优解,但同样在大规模问题上,效率不佳;智能算法,因其既能得到优解,又能保证效率的优点,得到许多研究者青睐。Osman[7]使用模拟退火以及禁忌搜索算法作为策略,在VRP上求得了不错的结果。Bullnheimer等[8]和Baker等[9],分别提出了一种改进蚁群算法、遗传算法,用于VRP,并将其与模拟退火算法和禁忌搜索算法效果相比较。Marinakis等[10]在粒子群算法中融合了局部搜索和路径重构策略,用于随机需求车辆路径问题中,取得了较好的效果。Zhang等[11]使用量子进化算法求解以路径及客户满意度两个方面为目标的多目标VRP。Marshall等[12]提出了基于语言进化的超启发算法,在解决问题域经验不足的情况下,同样可以求解VRP问题,并在实例中得到效果验证。
超启发算法(Hyper-heuristics Algorithm, HH)被称为“寻找启发式算法的启发式算法”,其主要由高层启发式策略(High-Level Heuristic,HLH)和底层启发式算子(Low-Level Heuristics,LLH)两个部分组成。LLH是对实际问题进行独立搜索,而HLH是对LLH进行科学合理的选择,并对产生的解判别接受。HLH设计主要指选择策略和解的接受准则两个方面。
超启发算法由于具有通用性、高效性等优点,已被广泛运用于多个领域。Cowling等[13]将超启发算法用于人员调度,减少了分配时间,提升了分配质量。Kheiri等[14]研究了基于序列分析的超启发算法,将其用于基准水网调配优化。邱俊荧[15]提出了基于带path-relinking的GRASP超启发算法,由构造底层算子序列阶段、局部搜索阶段和path-relinking阶段组成,并将其与模拟退火算法进行了比较。Walker等[16]在超启发算法局部搜索算子中添加自适应机制,将其用于带时间窗的车辆路径问题。Sabar等[17]提出构建蒙特卡洛树搜索框架的超启发算法,即将底层算子看作一棵树,用蒙特卡洛法识别其不同序列。Soria-Alcaraz等[18]对超启发算法的确定有效启发式子集进行了讨论,提出一种新颖的迭代局部搜索算子。Dokeroglu等[19]利用标准库中有关最新的元启发式,模拟退火,鲁棒禁忌搜索,蚁群优化和突破局部搜索算子,来解决二次指派问题。Zamli等[20]将禁忌搜索作为高层选择策略,将教学学习优化算法、全局领域算法、粒子群算法和布谷鸟算法作为底层搜索算子,改进超启发算法。Choong等[21]设计了基于强化学习的超启发算法,将Q算法用于高层选择策略,验证了其算法与其他性能最好的算法效果相当。
鉴于超启发算法优秀的搜索性能,而强化学习又能基于学习评价动作,本文将强化学习策略——深度Q神经网络(Deep Q Network,DQN)算法引入超启发算法的高层策略设计,旨在利用学习机制,对底层启发式算子立即奖惩、将来奖惩进行权衡;设置较优序列池,同时使用模拟退火的接受准则,更有效地引导底层算子搜索,获得优质解。并利用所提算法对CVRP进行求解,验证其性能。本文首先介绍了CVRP的描述与模型,然后构造了一种基于DQN算法的超启发算法,最后使用该算法对标准算例进行计算。根据仿真实验的结果,并与其他算法进行比较分析,证明了基于DQN算法的超启发算法在解决CVRP上的有效性。
1 有容量车辆路径问题
1.1 问题描述
CVRP描述为:假设有一个已知位置的配送中心,对多个已知位置和需求量的客户点进行货物配送。约束为:每个客户点有且仅有一辆车对其服务;每辆车有一定标准载重量;完成配送任务后,每辆车须返回配送中心。目标为:求在保证最小使用车辆数的前提下,所有车辆行驶的最短总距离(或最低总成本)以及路径分布。由于其是一个NP-hard问题,当客户规模较大时,传统的数学规划方式难以求解,而传统启发式算法、智能算法也容易陷入局部最优,无法获得全局最优解的情况。为此,设计能克服以上难点的算法,求得问题最优解,具有较大意义。
1.2 数学模型
将上述问题转化为数学模型[22]:配送中心设为i=0,客户点设为L(i=1,2,3,…,L),最多车辆数设为K(k=1,2,3,…,K),每辆车具有相同载重量为q,每个客户点需求量设为di(i=1,2,3,…,L),客户i到客户j的距离设为cij。定义以下变量:
数学模型如下:
(1)
(2)
(3)
(4)
且≠Φ∀k。
(5)
其中:式(1)表示所求目标函数,即最短总距离;式(2)为每辆车的标准载重量约束;式(3)保证每个客户点都被服务;式(4)保证每个客户有且仅有一辆车服务;式(5)表示消除子回路。
2 基于强化学习的超启发式算法设计
鉴于CVRP的NP-hard属性,设计了基于强化学习的超启发算法。利用聚类方式提升初始解的质量。在此基础上,将强化学习引入超启发算法的高层选择策略,为了更好地选择底层算子,设计常数Ck辅助判别State值,利用学习机制,主动记录在所有状态下算子的相对优劣性;结合模拟退火算法,选择性接收优劣算子。并设计序列池,动态存储当前序列,从而一定程度上扩大全局搜索能力。
超启发算法的设计主要包括以下几方面:初始解的设计;高层启发式策略HLH设计;底层启发式算子LLH设计;算法流程框架设计。
2.1 初始解的设计
对一个可行解的要求是:能够包含所有客户,且每个客户点只出现一次;在满足车辆标准载重量的条件下,粗略划分路径数,即大致确定由k辆车运输;每条路径起始点、终点皆为配送中心。如果在算法初期,给予较优质初始解,则有助于减少算法搜索的时间,提升效率。因此,本文采用聚类[23]的思想。但由于通常的聚类方法都需要不断迭代,寻找聚类点,为了降低选取聚类点产生的耗时性,本文将按距离最短选择聚类点,虽不能获得准确点,但已经能达到优化初始解的目的。
具体步骤如下:
步骤1对于第k条路径,先设配送中心点为i=L+1(也可设为“0”),即该路径两端点都为i=L+1;随机挑选客户点L(i=1,2,3,…,L),加入首尾点中间,判断该车辆现载重量情况。
步骤2从剩下的客户点中继续随机挑选,依次加入路线,直到超出标准载重量,则产生第k+1条路径;将超超出标准载重量的点,加入新路线中;重复循环,当所有客户点都被选取,则一个初始种群个体生成。
步骤3多次进行上述操作,生成一定数量个体的种群,数量为Npop。对Npop个个体进行路径判断,选出具有最短路径数的个体,记最短路径数为k,将k作为划分块的数量。
步骤4计算所有客户点与仓库点的距离ci-L+1(i=1,2,3,…,L)。为了节省聚类分类的时间,将ci-L+1升序排列,只取前k个点作为聚类中心点,设为LKC(KC=1,2,3,…,k),KC代表聚类块,以除聚类中心点外的其他客户点,与各聚类中心的距离最短为原则,进行聚类。
步骤5随机排列KC块,按车辆载重量分配,依KC块排列顺序,随机挑选客户。若KC块中客户点未能满足k车辆载重,则向KC+1块中随机抽取客户点,直至满足,反之则向后延用至k+1辆车,共组成k条路径,由此产生一个初始解个体。
2.2 超启发算法的高层启发式策略HLH构建
超启发算法的高层启发式策略HLH主要包括底层算子的选择策略和解的接受准则两方面。这两方面的设计是超启发算法设计的关键。对于底层算子的选择策略,本文将强化学习中的DQN算法[24-25]引入超启发算法。对于解的接受准则,本文利用模拟退火的接受准则,对劣势解选择性接收,引导解向较好效果的方向发展。
2.2.1 基于DQN的底层算子的选择策略
DQN算法主要基于Q-Learning算法的思想,利用当前状态State,下一步行动Action,下一步状态Statet,延用Q值的计算方法,建立损失函数,构建神经网络结构,起到预测下一步底层算子性能表现的作用。将DQN算法作为底层算子的选择策略,根据当前解的状态(或者解的发展趋势),挑选下一步底层算子。
(1)State设计
State表示事物当前的状态。设计目的:尽可能体现Action对事物产生的影响以及能够为挑选之后的Action起到预测选择作用。由于本文将算法用于求解CVRP,难以对State值提前划分确切范围,State值完全取决于各Action对解的适应度值的影响,同时为了在挑选算子中,保证解的多样性,State值在一定时期(未求到最优解的情况下),须在一定范围内不断变化。将State代表适应度值的变化程度,设计当前代的适应度值为fit,上一代的适应度值为fit′,上一代的平均适应度为avg(fit′),设计State的表达式为以下两种:
State=-(fit-avg(fit′))/avg(fit′),
(6)
State=-(fit-fit′)/fit′。
(7)
对以上两个表达式进行实验仿真,设初始状态为“0”,结果如图1所示。
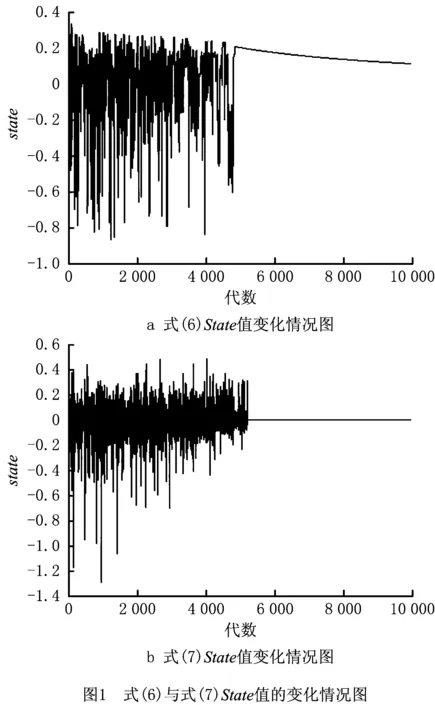
由图1可得,两式在一定代数之内State因外部环境都呈现上下摇摆的情况。但是式(6)容易在求得局部最优解后,随着代数的增加,呈现“假State”状态,此时的fit=fit′为局部最优值,一直未发生变化,但State由于
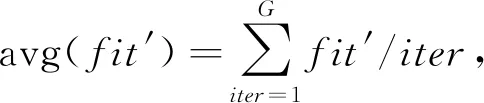
(8)
式(8)中分子增长后的值小于分母(iter为迭代次数),整体呈现逐渐下降趋势,是对当前状态的错误反应。而式(7)表示的State值在局部最优后稳定为0,正确反映当前状态,有利于算法对产生局部最优状态的判别,更符合设计要求。
因为在此类求最优问题中,单纯的运行趋势无法确切表示当前状态。在算子选择中,本文采用了3种类型的算子,将其分为局部优化算子与变异算子两大类,鉴于两类算子优化性能不同,为了更好地体现算子对当前状态的影响,添加State值的辅助判别机制:利用常数Ck值,作为State基数,需满足的条件为,对State值的影响远大于由fit值变化引起的影响(起到区分算子种类作用,利于后续求解算子奖惩值),经测试观察,fit值变化引起的式(7)大小变化范围见如1右图所示,值约为[-1.4,0.6],变化区间的长度约为2。经分析,若局部优化算子Ck=10,变化区间长度占Ck值的20%,影响较大,基准性较差;取局部优化算子Ck=20,变化区间长度占Ck值的10%,满足既能扰动State值,且影响较小的条件;取局部优化算子Ck=60,变化区间长度占Ck值的3%,扰动性较低。因此,最终选择局部优化算子Ck=20。因为基准值越大,State值越大,越容易被选择。且由于变异算子较局部优化算子效果更具间接性,即变异算子根据适应度值较优的准则不容易被选择,为了平衡两种算子被选择的概率,定变异算子的Ck值为局部优化算子的2倍,变化区间长度占Ck值的5%。由于变异算子相较于局部优化算子优化效果更间接性,定变异算子的Ck值为局部优化算子的2倍,变化区间长度占Ck值的5%。因此定义如下:

则
State=-(fit-fit′)/fit′+Ck。
(9)
(2)Action,Reward设计
由于本文在HLH中使用算法的目的是选择LLH的算子,利用算子在问题解的空间中,搜索优质解,Action值为LLH算子的指代值(如算子“1”,算子“2”……)。
在考虑State值时,已经对算子种类进行对应区分,因此扰动算子的Reward值判断方法,不再区别于其他种类算子。因此,利用Reward代表立即回报值,若当前解的质量比上代解的质量提升,则Reward=1;未提升则Reward=0;质量下降,则Reward=-1。
(3)DQN算法主要结构部分设计
DQN算法结构中主要包括经验池、估值网络、目标网络。
为了提供历史经验,对Q值计算提供参考,在DQN算法中设计经验池(Experience Pool, EP)。EP存储的是NE组数据,N代表经验池的容量。每组数据由State,Action,Reward,Statet四个部分组成,记录的是当前事物状态以及进行下一步动作后的立即回报值和下一步状态值。
传统的Q值计算与神经网络相结合的算法,只采用一个神经网络,若其中具有错误历史(即某个连续时刻,某个动作奖赏极大),则会使该动作的Q值评价大于实际性能水平,因此设计估值网络与目标网络来均衡历史的影响。估值网络与目标网络是同结构的神经网络。包含同样的隐藏层数及结构,以及相同个数的神经元节点。输入层节点数根据State输入值设置为一个,输出层节点数根据低层算子数量进行设置。利用随机,初始化估值网络的阈值ωe、权值be以及目标值网络的阈值ωt、权值bt。估值网络的输入值为NE组中某一组的State,目标值网络的输入值为对应组中的Statet。在估值网络输出值中取对应第NE组中Action所对应的Qe,即Qe(Action),而在目标值网络的输出值中取最大的输出值max(Qt),将两者根据下式进行计算,作为更新估值网络的损失函数值的判断:
Loss=((Reward+γ·max(Qt))-
Qe(Action))2。
(10)
根据Loss值,对ωe和be作更新处理,其中γ为折扣率。一定代数以后,将ωe和be分别替代ωt和bt,以此更新目标网络。利用更新后的估值网络,对当前状态的下个动作产生的影响进行预测,根据预测情况选择Action值。
2.2.2 解的接受准则
接受准则的目的就是判断是否需要用当前解代替先前解。当产生改进解时,必然接受;当产生非改进解时,一律接受,容易使算法整体运算缓慢;一律拒绝,则会导致种群缺乏多样性,最终陷入局部最优的情况。因此,接受准则对算法的收敛速度及优化精度有很大影响。张景玲等[26]采用模拟退火算法(Simulated Annealing, SA)作为接受准则,取得了不错的效果,因此本文也引用其作为算法的接受准则,以概率p选择性接受非改进解,
p=exp(ΔE/Tk),
(11)
Tk+1=Tk·β。
(12)
其中:ΔE表示算子作用后,前后解的质量差,β表示降温系数,k为温度计数器。
2.2.3 搜索空间优化
本文的主体搜索方式为先分配后排序,以减小搜索空间的目的进行设计。由2.1节可知,采用先将客户点按载重分配,在满足载重的条件下,进行顺序优化的方法。在算法过程中,采用缩小解的搜索空间的思想[27]设计序列池(Sequence pool,SP),保存算子优化后得到的最优解序列(一辆车的路径),进行后续搜索。如图2所示。
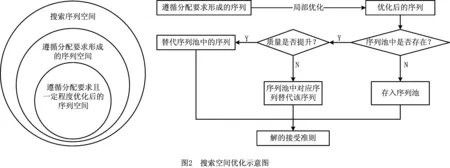
图2左图代表搜索空间所属,可知如果没有任何约束,只对序列进行排序,则搜索空间最大;若利用载重等约束条件进行限制,则相对缩小了搜索空间;在约束后的基础上,再次进行序列的优化,则能获得更小的搜索空间。图2右图代表实施过程,即因为采用局部搜索算子优化后,所得的序列(每辆车的路径分布)都是较优序列,搜索序列池,判断是否存在该序列点集。若不存在,则直接存入序列池;存在则对比,替代该序列或者更新序列池。
2.3 超启发算法的底层启发式算子LLH设计
根据VRP的特点,设计对应的几种算子,主要为局部优化算子(Local Research,LLH-L)、变异算子(Mutation,LLH-M)和破坏与重构算子(Location-based Radial Ruin,LLH-LR)3大类。将变异算子与破坏重构算子合为一类,具体算子为如表1所示。
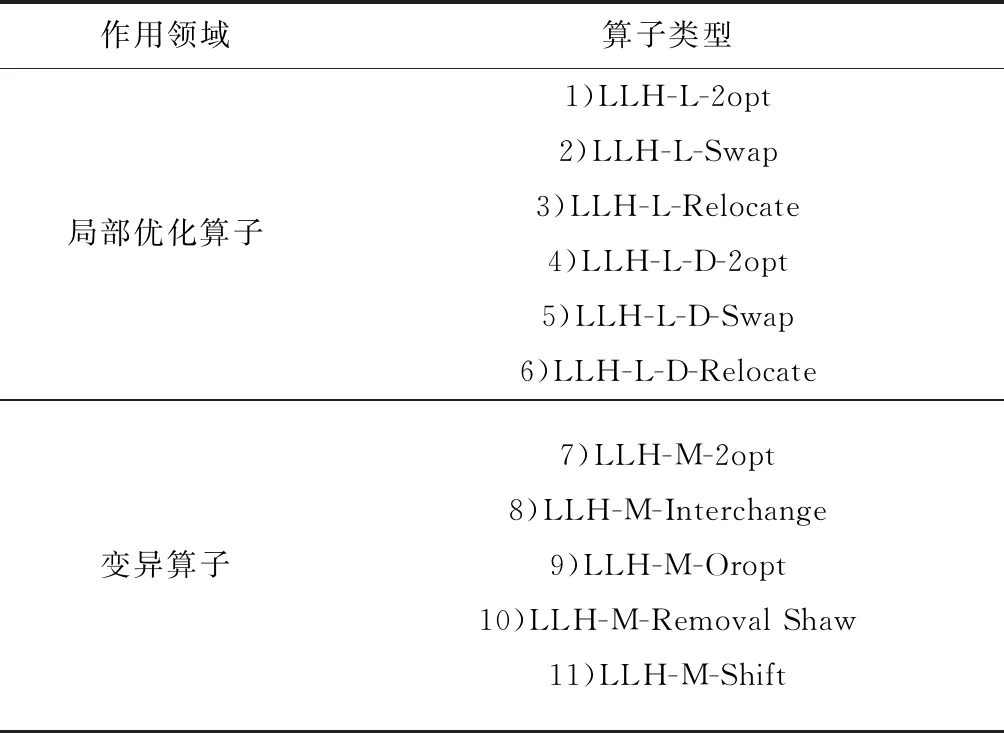
表1 底层算子表
将其根据作用分类是为了方便设计State的基数。局部优化算子主要通过点或者部分交换以及重定位的方式,对路径进行优化,作用后能够绝对判别作用效果(Reward值大,则效果好,反之效果差);变异算子主要起到扰动作用,作用后作用效果并非可以绝对判别。1)~3)是路径内局部优化算子;4)~6)是路径间局部优化算子;7)~11)为变异算子。
2.4 基于强化学习的超启发式算法框架设计
利用DQN算法的学习机制,对在不同状态下,使用不同LLH算子对解产生的影响作评价,保留较优序列和较优解,由此选择相对较优的LLH算子进行解的搜索,设计如下算法流程(如图3):
步骤1初始化。先生成Npop组个体的种群,得到使用的最小车辆数为k,利用聚类思想将客户点区域划分为k块,称划分成的每块区域为“KC块”,由KC块随机挑选生成可行解组P(pi=p1,p2,p3,…,pNP),计算种群适应度f(fi=f1,f2,f3,…,fNP)。随机挑选一组可行解pi以及对应适应度值fi,设PB为最优解个体,FB为最优适应度值,设LLH算子数量为NA,Action取值为(1,2,3,…,NA)整数,初始化PB=pi,FB=fi,State=0,Action=random(NA)(随机挑选一个范围NA中的数)。
步骤2经验池、序列池存储。操作上步Action后,产生的个体为Ind,适应度值fit,根据适应度值,判断立即回报值Reward,此时状态即为“下一个状态”,判断该State和Statet所属状态,利用式(12)计算Statet值。设EP代表经验池,将上述值存入,则EPnE=[State,Action,Reward,Statet],nE代表经验池中数据组数。当达到一定次数后,判断此时State值所属状态,如果为15≤State≤25,则此时Action为路径内算子,对此时的序列进行筛选,质量优则存入SP,SP代表序列池,反之,则更新序列。SP设常量Qsp为容量,且每次对比SP中序列,若此时序列在SP中有对应序列集,则SP中该序列计数一次。当SP容量已满,则刷新对比次数最少的序列。
步骤3解的接受保留。判断,如果fit
步骤4判断经验池容量。判断经验池内组数nE,n≥NE,则进入步骤7学习环节,否则,进入步骤5选择Action步骤。
步骤5选择Action。设置epsilon值,若随机值>epsilon,将State值,输入估值网络,输出Qe值,取max(Qe)所对应的Action,若随机值 步骤6保留全局最优解,判断算法是否结束。若fit≤FB,更新全局最优解,FB=fit,PB=Ind,否则保留原有解。若nG≥G,返回步骤2,否则算法结束。 步骤7选择学习样本,并初始化神经网络。从EP中随机挑选NS组,作为学习样本,记为ESP。初始化估值网络和目标网络的阈值和权值ωe、be、ωt、bt。 步骤9更新目标值网络。判断学习代数Ln≥LN,则令ωt、bt替代ωe、be的值。 步骤10判断学习结束情况。若学习代数Ln≤(3/4)×NS,则进入步骤8继续学习更新。反之,则进入步骤5选择Action,返回主循环。 对算法的时间复杂度进行分析是对算法运行时间性能的一种评估方法。本文算法为基于强化学习的超启发算法,简称为HH-RLDQN。影响本文算法的复杂度计算的因素有:初始化种群的种群规模NP,客户数量N,车辆数量K,迭代次数Gmax,底层算子数量为NL,序列池容量SP,神经网络中学习样本数量LN,神经网络的隐藏层节点数HN。 对本文算法计算时间复杂度:随机化初始并聚类种群复杂度为O(2×NP×N2+NP×K),计算适应度值复杂度为O(NP);高层策略中,求解经验池(State, Action, Reward, Statet三个值的求解以及写入经验池)复杂度为O(1+1+1+1),每次所得序列与序列池中序列的对比次数设为最大值(与全池序列对比)复杂度为O(SP),接受策略复杂度为O(1),神经网络学习复杂度约为O(LN×(HN+3×HN+1)),选择Action选耗时更长复杂度为O(HN);底层算子执行,由于每一步选择的算子未知,选择耗时最长的算子复杂度为O(N2)[28]。算法迭代一次的复杂度约为O(2×NP×N2+NP×K)+O(NP)+O(4)+O(SP)+O(1)+O(LN×(HN+3×HN+1))+O(HN)+O(N2),算法总体计算复杂度约为: O(HH-RLDQN)=O(2×NP×N2+NP×K)+ Gmax×(O(NP)+O(4)+O(SP)+O(1)+ O(LN×(HN+3HN+1))+O(HN)+O(N2)) ≈O((Gmax+NP)×N2+Gmax×LN×HN)。 (13) 由式(13)可得,算法的总体复杂度约为O((Gmax+NP)×N2+Gmax×LN×HN),即高层策略的复杂度除了神经网络部分,其他忽略不计。本文算法复杂度主要的影响因素还是迭代次数Gmax,初始化种群的种群规模NP,客户数量N,神经网络中学习样本数量LN,神经网络的隐藏层节点数HN。文献[29-30]中计算总体复杂度用本文符号表示都为O(Gmax×NP×N2),因为 O((Gmax+NP)×N2)< NP×N2)且HN≈NP。 (14) 本文的神经网络中学习样本数量LN取值范围始终小于1 000,则LN≤N2恒成立,即 O((Gmax+NP)×N2+Gmax×LN×HN) ≤O(Gmax×NP×N2), (15) 式(15)恒成立。由上述分析可得,本文算法的计算复杂度与其他群体智能进化算法计算复杂度在同一个量级,在计算机计算的可承受范围之内。 实验环境Intel(R)core-i5-3230M, 12 GB RAM,MATLAB语言编写程序。经过反复测试,程序中使用的参数有Q值函数中折扣率γ=0.8,epsilon初始值=0.5,迭代最大代数Gmax=10^6,经验池NE=800,学习挑选样本NS=600。 实验利用HH-RLDQN,对CVRP的标准算例进行求解。分别选取Set A,Set E和Set P的标准算例求解,对每个算例计算20次。所有算例可在网址:http://neo.lcc.uma.es/vrp/vrp-instances/capacitated-vrp-instances/下载。其中算例最优距离解(BK),实验所得最优解距离解(Min),所得最优解距离解平均值(Avg),实验所得最优解与算例最优解误差(DEV%)(DEV=(Min-BK)/BK)。 表2为本文使用的HH-RLDQN算法及文献[29-32]对Set A标准算例的计算结果。表中加粗且标有“*”的数字表示求得当前算例最优解。由表2可知,文献中的LNS-ACO和SC-ESA两种算法都求得27个算例中的17个算例的最优解,求最优解成功率为62.96%;HVNSOS算法求得20个最优解,求解成功概率为74%;NHQEA算法求得23个最优解,求解成功率为85.18%。本文算法求得22个最优解,求解成功率为81.48%,相较于前两种算法,提升18.52%,提升较为明显,相较于第3种算法提升7.48%,具有一定优势,相较于第4种算法,仅低了3.7%。求得各算法对于该27个算例最优解的误差率平均值分别为:0.6%,0.16%,0.13%,0.07%,本文算法的误差平均值为0.07%,相较于前3种算法降低了0.53%,0.09%,0.06%。值得一提的是,本文算法在低于NHQEA算法最优值求解成功率的情况下,仍与其具有相同的误差平均值。在求解n61,n64和n65这3个算例上,本文算法在本次实验中相较于NHQEA算法,具有一定优势。对于20次实验的最优值平均值观察可得,有8个算例平均值均达到算例最优值,除n69和n80算例,平均值与算法所得最优值相差为9和13,其他算例差值均在[1,6]之间,可见本文算法在此些算例中求解具有相对准确性。由此可得,本文算法相对于多种群搜索的其他4种算法而言,在Set A标准算例上,具有较好的搜索效果。 表2 CVRP Set A-标准算例测试 续表2 表3是本文使用的HH-RLDQN算法,及文献[31-32]对Set E标准算例的计算结果,表中“~”表示文献中并未给出计算值。由表3可知,LNS-ACO和SC-ESA两种算法分别求得8个算例中的4和5个算例的最优解,求最优解成功率为50%和62.5%;本文算法求得9个算例中的5个算例最优解,求最优解成功率为55.56%,求最优解成功率与两种算法效果相同。求得两种算法对于8个算例的最优值平均误差率为0.68%和0.63%,本文算法为0.32%,分别下降0.36%和0.31%,几乎为一半,尤其在n76-k7和n76-k8算例上,误差率仅为0.01%和0.03%,效果相较于两种算法,极其优秀。由以上数据可知,本文算法,在Set E-标准算例上相对于LNS-ACO和SC-ESA同样具有较好搜索效果。 表3 CVRPSet E-标准算例测试 表4为本文使用的HH-RLDQN算法及文献[29-32]对Set P标准算例的计算结果。由表4可知,除了SC-ESA算法整体搜索求解效果不是很理想,17个算例中,只求得6个,LNS-ACO,HVNSOS,NHQEA以及本文算法都具有较好的搜索求解效果。LNS-ACO,HVNSOS,NHQEA在17个算例中求得最优解算例的个数分别为12,13和13个,求最优解成功率分别为75%,76.47%和76.47%,本文算法求得最优解算例个数为16个,求最优解成功率高达94.12%,较3种算法提升近20%左右。本文未求得的算例n50-k10,NHQEA算法同样未求到,且求得为同值697,差值仅为1,误差率为0.14%。在平均误差率上,由于本文算法就一例未求得,故仅为0.02%,相较于其他算法分别降低0.51%,0.65%,0.08%,0.02%。本文算法对表中前7个算例实验中平均值求得算例最优值,除n50-k8算例,其余算例与平均值差值范围均为[1,6],具有较强准确性。 表4 CVRP Set P-标准算例测试 图4所示为本文算法在Set A/P标准算例实验中所得平均值与最优值偏差,对两种类型的算例,平均值与所求得的最优值之间相差几乎不大,44个例子中,只有2例偏差在[10,15]之间,1例为30(原因为各车容量相对紧凑,造成实验结果一直在最少车辆数为8和9之间交替出现,且当9辆车时最优值甚至求得629,小于8辆车的最优值,而出现8辆车的最优值实验结果742,远大于实验目标最优值),其余全在[0,6]之间,充分反映了本文算法的求解稳定性。 图5所示为计算Set E客户点数为50标准算例,所得的DQN神经网络收敛图。纵坐标为网络的均方误差值,横坐标为学习代数。在算法中设定,经验池刷新一定值后,才重新进入学习,因此横坐标代数少于实际算法运行代数,由此导致在算法中,学习代数不多,最后收敛时,均方误差为0.016 7,未达到稳定状态。且其中变异算子并非绝对优化效果,即使在同样的State值情况下,依旧可能会出现负优化,造成样本数据偏差,因此图中曲线有起伏,但整体仍呈现下降趋势,体现了较好的学习情况。均方误差值逐渐减小,则DQN神经网络部分越接近真实,对底层算子性能的评价及其选择也越准确,提升超启发算法整体的搜索能力,算法的效果从之前的结果表、图中已经得到了体现。 通过上述3种标准算例的计算结果,可得本文所设计算法能在CVRP上得到了较好的效果,在保证能求得较多最优值的情况下,多次实验的平均值均接近最优值,从而表明算法具有较强的搜索能力和稳定性。通过与其他四种算法的对比表明,实验总体效果优于LNS-ACO算法和SC-ESA算法,较优于HVNSOS算法,与NHQEA算法效果相当,但在小客户点算例上,本文算法较NHQEA算法具有相对更好的搜索求解效果。 本文提出了一种基于强化学习的超启发算法求解有容量车辆路径问题。在初始种群的设计中,引入聚类思想,提升初始解的质量。在超启发算法高层策略设计中,引入强化学习中的DQN算法,结合Q学习算法的思想与神经网络算法的结构,对底层算子在解的每个状态下表现的性能进行评价,评分由立即奖惩和将来奖惩两部分组成,同时利用模拟退火的接受准则以及序列池,对得出的非改进解有条件接受,引导算法跳出局部最优情况,向优质解的空间持续搜索。 利用所提算法对CVRP三种标准算例进行实验求解,将求解所得结果与目前最优结果和文中所提4种其他算法所得结果相比较,通过最优值、误差率和平均值分析,验证了本文算法在该问题的求解上具有相对准确性和稳定性,总体求解效果优于对比算法。 下一步的工作将尝试采用该算法求解CVRP大规模客户点的问题及其衍生问题。同时,虽然本文算法在实验求解中整体获得不错的效果,但在客户规模较大的车辆路径问题上,仍具有较大的改进空间,之后将继续优化其高层策略,争取有所突破。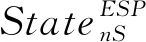
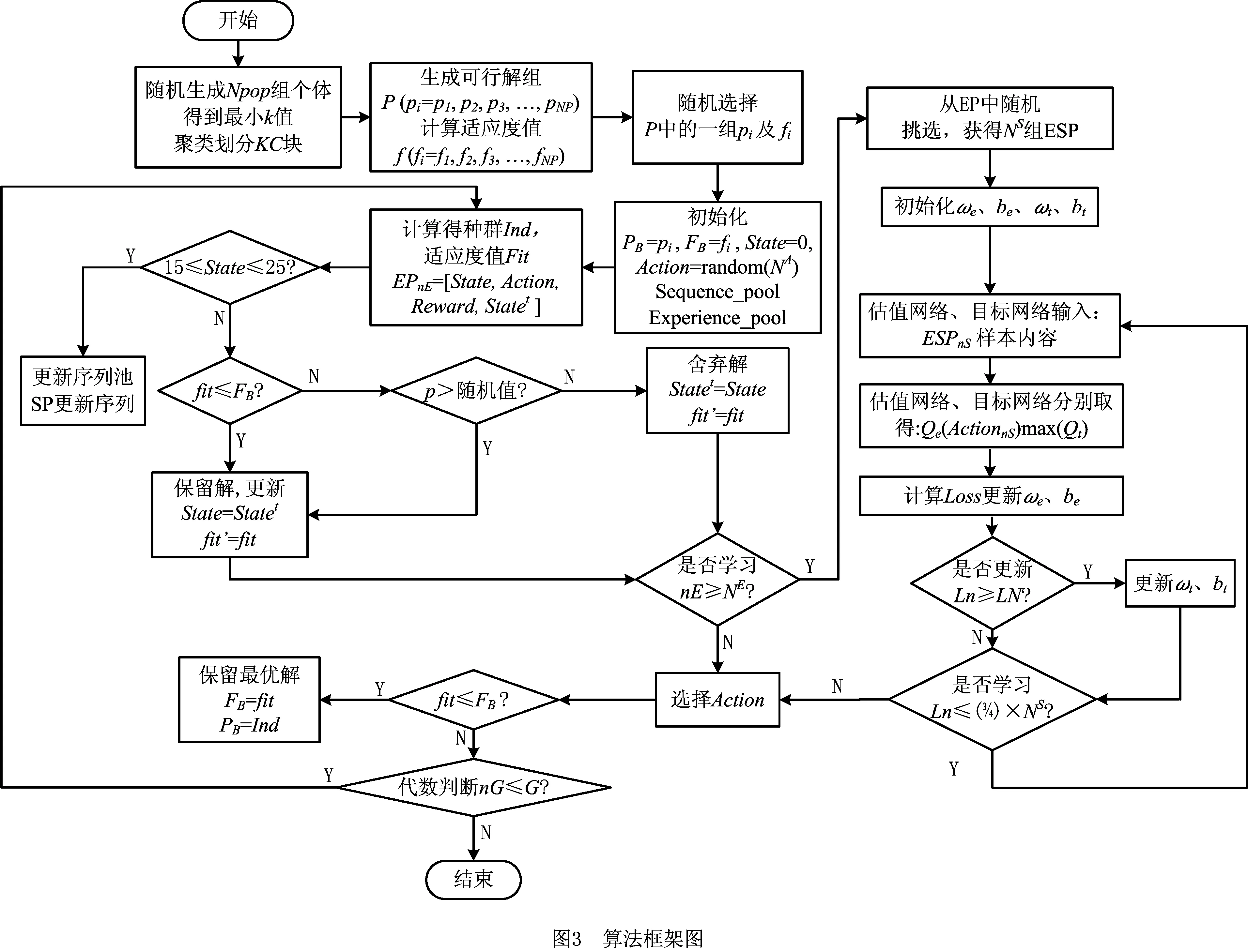
2.5 基于强化学习的超启发式算法复杂度分析
3 数值实验
4 结束语

