基于同步观测信息利用的高寒湖泊湍流通量数据插补方法*

靳 铮，张雪芹

(1：中国科学院地理科学与资源究所,中国科学院陆地表层格局与模拟重点实验室，北京 100101) (2：中国科学院大学，北京 100049)

涡动相关(eddy covariance, EC)方法在国内外湖泊水热和成分通量观测研究中均有广泛应用[1-6]. 太湖在2013年就建成了由6个通量站组成的中尺度涡动相关通量观测网[3]，并利用观测数据分析和模拟了该地区湖气间能量、水热相互作用. 2014年鄱阳湖的涡动相关研究[5]为大型浅水湖湖面能量通量划分了不同的水文过渡期格局. 洱海[7]和纳木错[8]的涡动相关观测研究初步揭示了高寒湖泊的水面湍流通量特征. 受制于仪器性能和观测下垫面的异质性，EC观测的通量数据时间序列会产生缺测点[9]. 缺测点产生的原因主要包含信号异常、仪器损坏以及湍流平稳性统计未能满足通量计算假设等[10]. 特别是高寒湖泊EC观测面临着封冻期维护、强风和低温等问题. 因此，EC系统一般采取岸基或近岸安装[11-13]. 这使得EC系统所测来自陆面源区的通量数据和湖面源区的混杂一起. 通量源区划分并提取目标源区通量数据后，EC观测的有效数据比例显著下降. 湖面源区通量数据有效数据时间分布存在显著的不均匀现象，从而严重影响EC通量数据的可分析性，因此有必要对EC通量数据进行插补. 湖面水热通量观测研究中，学者们把温度梯度、风速、水汽压差等作为湍流传输过程的基本物理背景信息来估算通量强度(如Bulk Aerodynamic Transfer Model[13]和DYRESM[14]). 这类种估算方式除了考虑动力、热力机制之外，还需考虑物理量纲的对应，以便将估算模型以等式的形式表达出来. 但是湍流输送过程的时空尺度决定了这类梯度量纲模型不足以描述湍流传输在其宏观特征背后的微观过程. 除此之外，通量数据的插补还可以使用查表法[15]、动态线性回归方法[16]和非线性回归方法[17]等基于统计原理的方法. 这类方案是根据观测经验，以温度梯度、水汽压等关键背景物理信息为依据，通过拟合计算得到对通量强度的最优统计估计来完成插补的. 相对于上述方案而言，ANN(artificial neural network，人工神经网络)方法可以更加充分地利用羊卓雍错观测实验中较丰富的辅助观测系统和较长观测时间带来的数据量优势. 由于羊卓雍错的特殊近地层湍流背景[18]，湍流输送过程在此处与其背景动力、热力强迫过程的关系更加复杂，非线性特征更显著. 故本文在温度梯度、风速、水汽压差等核心要素的基础上，将更多的环境气象要素同时引入到湍流传输物理背景信息的描述中，并使用ANN模拟当前信息组合与通量强度值的映射关系.

尽管以ANN为基本工具的机器学习方法广泛应用于地球科学研究中[19]，但其在湖泊通量观测的数据插补方面仍有待加强. 洱海EC通量观测实验[7]使用了一个神经元总数20个以内的ANN模型来模拟和插补通量数据，其ANN模型输入变量包含风速、水面温度、气温、饱和水汽压差4项. 但该研究对ANN模型估算通量强度的准确性未作进一步讨论. 由于ANN模型的性能取决于数据所包含的有效信息量和噪声水平[20]，故其模拟性能的检验是必要的. 我们从信息利用的角度设计了一种针对EC湍流通量数据的ANN模拟插补及验证方案. 通量模拟输入信息中增加变量时，信噪比较低的变量会影响ANN模型的性能，同时大幅增加ANN训练时间. 为了给输入ANN模型的大量有效信息和噪声组合提供充足的概率样本空间定义域，本文采用了超宽ANN结构[21]. 基于超宽结构的ANN模型神经元总数超过2000个，本研究利用并行计算技术解决了模型训练的时效问题. 本文对上述超宽结构ANN模型的通量估算性能进行了交叉验证和误差分析，提供了客观且全面的验证结果和误差分析结论，并讨论了EC湍流通量数据插补问题中ANN模型的泛化，为高寒湖泊湍流通量观测研究的数据插补提供了一种参考思路.

1 数据与方法

1.1 羊卓雍错涡动相关观测

羊卓雍错湖湖面面积约为643 km2[22]，是喜马拉雅山脉北麓最大的内陆封闭湖泊. EC设备及辅助观测系统的设置地点为羊卓雍错湖靠近浪卡子县白地水文站的近岸浅滩(29°07′28″N, 90°26′27″E)，海拔高度4420.63 m. 为避免被湖泊封冻期前后的冰凌冲击摧毁，通量设备于每年的1月上旬进行拆卸，3月下旬重新安装. 本研究采用通量系统2016年和2017年非封冻期同一观测时段(4月3日0：00-12月31日23：30)的水热通量、湍流、气温、湿度、水面温度和水面辐射等同步观测数据. 此外，2016年3月30日-4月2日以及2018年1月1-4日的数据将用于测试ANN模型的时间扩展性能，不参与ANN模型的训练及交叉验证. EC设备信息与数据采集的详细情况见参考文献[20].

1.2 神经网络建模与检验方法

1.2.1 同步观测变量的特征工程 特征工程是对ANN输入数据进行标准化处理的过程[23]，原始同步观测数据经过特征工程转换为可直接输入ANN的特征向量. 特征向量的处理方式对ANN的训练时效和模拟性能均有重要影响. 本文使用ANN方法进行通量强度与同步观测特征间的映射关系拟合，输入ANN的同步观测特征变量有12个：气温、水面温度、平均水平风速、平均湍流动能、莫宁-奥布霍夫稳定度参数[24]、气压、饱和水汽压、水汽压和四分量长、短波辐射. 上述加入输入数据样本的特征变量除了与涡动通量强度观测值同一时刻的30 min平均值外，还包含它们前后各30 min的平均值，故ANN的输入特征向量维度为36. 同步观测特征变量的标准化处理采用平移缩放法，即根据各个变量的强度概率密度分布剔除异常值后平移并缩放至[0, 1]区间. 训练样本由处理完成后的同步观测变量特征向量及观测通量强度序列组成. 由于ANN模型具备较强的非线性映射拟合性能[25]，本研究特征变量选取时并不考虑所选变量和通量强度的统计相关性，而只需要特征变量与湍流输送过程的热力、动力过程存在理论关联即可.

1.2.2 建模框架与参数调试 本文使用Google®的开源机器学习框架TensorFlow[26]进行ANN模型参数化构建及训练，并使用Keras[27]开源Python模块对TensorFlow的功能框架进行调用. 为了保证映射关系拟合计算的时效性，本文采用CUDA®(Nvidia®, Inc.)并行计算方案，硬件计算单元型号为GTX-1080®，峰值性能为每秒9万亿次单精度浮点运算(9 TFLOPS). ANN的初始化模型采用密集连接结构，不加入偏差项神经元，损失函数为训练样本的平均绝对误差，拟合方式为随机梯度下降算法[28]，并利用随机参数剔除[29]方案弱化过拟合效应. ANN的激活函数采用PReLU[30](Parametric Rectified Linear Unit)和Tanh[31](Hyperbolic Tangent)，Tanh函数用于激活ANN的第一个隐藏层，PReLU函数则用于激活ANN的输入层和连接输出层的隐藏层. 已有研究表明隐藏层宽度于一定的范围内增加时，ANN可以对非线性过程作出近似与牛顿迭代法的线性求解[21]. 所以，本文参数调试采用隐藏层宽度指数递增搜索的策略，从初始化的16个隐藏层神经元开始，逐步增加隐藏层神经元至2n个，确定了合适的隐藏层数与神经元数后，再对学习率、剔除率和训练次数等参数进行调优.

表1 ANN参数设置的搜索结果

*平均学习率和平均迭代次数为10批次扰动训练的平均值.

1000 h(计算单元满载运行时间)左右的参数调试结果表明：浅层超宽密集连接结构的ANN对涡动通量具有较好的模拟效果. 表1为Keras机器学习模块下ANN设置参数的搜索结果. ANN的两个隐藏层神经元数量分别达到2048和1024个，这种超宽结构可以为不同质量、不同量纲的输入物理变量组合提供较大的概率空间，从而在迭代过程中搜索更多的映射关系，实现输入信息的充分利用. 由于感热通量、潜热通量和水汽通量所映射的同步观测特征是相同的，而通量强度数据的噪声不同. 故上述3种通量的拟合采用相同的ANN结构，只是利用不同的学习率和迭代次数来适应它们的噪声水平. 搜索计算所得的ANN模型虽然只有两个隐藏层，但两个隐藏层宽度均达到212个神经元后ANN的权重矩阵包含的权重数量已经超过1.6×107个，一次模型拟合所需训练时间超过12 h. 3109个神经元的ANN模型在对应的训练迭代次数(表1)上已经接近收敛，每100次迭代的梯度波动率小于0.01%. 考虑到实验的时效性及模型的收敛情况，我们未继续进行更大规模的ANN拟合计算.

1.2.3 折叠交叉验证 本文采用折叠交叉验证方法[32]对机器学习算法的性能进行了评估，并选取了10次折叠的交叉验证方案. 首先，我们按通量数据的强度概率密度分布将训练样本分割为10个折叠子样本，使各折叠子样本的通量数据均具有和原始样本相近的强度概率密度分布和平均值，并且在观测时段内均匀排列. ANN模型拟合计算时使用其中9个子样本合并进行训练，保留1个子样本用于验证模拟效果，然后交换用于验证的子样本. 在对10个子样本分别进行效果检验后，统计其平均结果和波动情况，以得到模型的误差期望和稳定性估计.

在搜索计算试验中，虽然10组训练子样本数据所驱动的ANN结构及拟合参数是相同的，但是由于ANN拟合计算采用了随机梯度下降方法，拟合后所得的模型权重参数在每一组交叉验证模型中存在微小差异，所以有必要分析各交叉样本模型性能的稳定性. 基于湍流输送过程的高度非线性[33]和ANN模拟输出可能产生的正负误差对称性[34]，本文基于10组经过验证的ANN模型，额外增加了10批次的拟合计算试验(共100个ANN拟合扰动模型). 我们对每一批次ANN模型的拟合参数进行了微调扰动，训练了共计110个ANN模型作为备选集合成员. 而后以平均绝对误差的方差最低为标准，我们选取了10个成员对通量强度进行集合模拟取平均，以进一步降低最终模拟结果的不确定性.

2 羊卓雍错通量数据插补及验证

2.1 湖面水热通量数据插补

表2 插补前后湖面通量的时间覆盖率

插补前后通量强度数据的时间覆盖率差异显著(表2). 湖面通量与陆面通量源区划分以及低质量等级数据剔除后，观测期间通量数据时间覆盖率均降至40%以下. 由于仪器故障，2016年的潜热通量和水汽通量数据从10月中下旬开始大量出现异常状况(如水汽瞬时数浓度测定值为负). 为减缓仪器故障对数据可靠性和整体噪声造成的影响，本文剔除了2016年9月30日以后的全部潜热通量和水汽通量数据. 故2016年的潜热通量与水汽通量时间覆盖率(26.4%)相对感热通量而言更低，同时也低于它们2017年同期的水平. 通量数据插补后仍有少量缺测(比例低于2%)，这与输入ANN模型的同步观测特征值缺测或异常有关.

2.2 折叠交叉验证

10组折叠交叉验证的结果(表3)显示：ANN模型的通量模拟性能十分稳定，各个交叉验证分组之间的误差波动较小. 对称性平均绝对百分比误差(SMAPE)[35]作为验证模型性能的关键指标，感热通量10组交叉验证中的平均值为31.871%,潜热通量与水汽通量的交叉验证中的平均值分别为20.8%和20.7%，这表明ANN模型对潜热通量和水汽通量的模拟效果优于感热通量. 这种差别产生的原因是感热通量观测数据的噪声水平高于潜热通量和水汽通量. 平均绝对误差(MAE)在3种通量的各10个交叉验证组中的平均值为5.4 W/m2、15.7 W/m2和0.35 mmol/(s·m2).MAE与通量观测平均值的百分比可作为通量模拟的期望误差. 在感热通量、潜热通量和水汽通量的观测平均值分别为18.8 W/m2、81.5 W/m2和1.84 mmol/(s·m2)的情况下分别为28.7%、19.3%和19.2%. 半小时分辨率下，潜热通量和水汽通量的模拟期望误差相对较小. 对于通量强度的观测期平均值而言，感热通量、潜热通量和水汽通量的期望误差分别为2.0%、1.3%和1.8%. 这由它们在10个验证组中各组的观测值平均与模拟值平均计算得出. 通量模拟的整体平均值误差期望远小于半小时分辨率单个数值的误差期望，原因是通量模拟误差的正负对称性较好(图1)，参与平均计算的模拟值越多，整体平均值模拟误差就于0的附近越稳定.

10次交叉折叠验证表明，MAE差别最大的验证组之间回归分布状况却十分接近，模型性能在10个交叉验证组间的波动很小(图2). 这反映了10组折叠交叉验证的样本分割具有良好的均一性. 模拟误差在不同的通量强度下的分布不均匀，感热通量对于0～15 W/m2之间时模拟误差明显更小，潜热通量和水汽通量于数值较大时模拟误差将增大. 这种现象出现的原因是超宽ANN对数据量有较高的敏感性，通量强度数据的概率分布在一定程度上符合正态分布，高值和低值数据所占比例相对于平均值附近的数据更少. 由对称绝对百分比误差(SAPE)的分位数分布(图3)可见，SAPE的平均值于各个通量的10组交叉验证中均大于其中位数，表明多数情况下模拟误差小于模型误差期望.

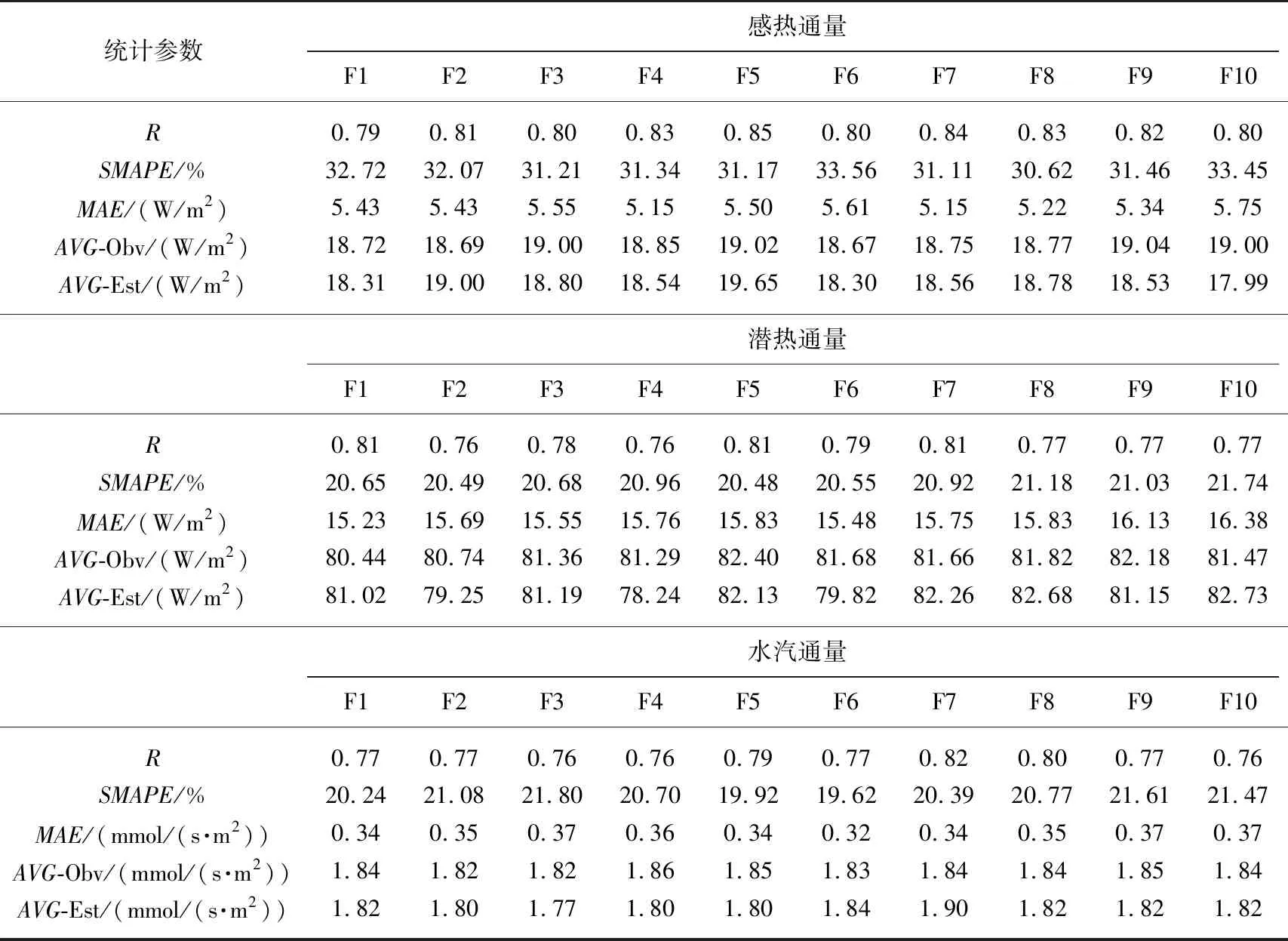
表3 ANN模型的10组折叠交叉验证结果*

*R为Pearson相关系数[36]，SMAPE为对称性平均误差百分比，MAE为平均绝对误差，AVG-Obv为观测值平均值，AVG-Est 为模拟值平均值，F1～F10为10个折叠组的编号.

图1 ANN模型模拟误差的概率密度分布Fig.1 Probability distributions of bias in ANN estimated fluxes

图2 10次折叠交叉验证中平均绝对误差最大和最小的验证组的回归分析结果对比(回归结果均通过了99.9%的置信区间检验，F1、F3、F6、F7和F10为折叠组的编号)Fig.2 Comparisons between the minimum and maximum mean absolute error of regression analysis results in 10-fold cross-validation groups

图3 10个交叉验证组的对称性绝对百分比误差分位数箱线图(F1～F10为10个折叠组的编号)Fig.3 Quantile boxes of symmetric absolute percentage error in 10-fold cross-validation groups

本文在计划修复的观测期(4月3日0：00-12月31日23：30)之外截取了两段未参与ANN模型拟合的数据，对比了ANN模型的模拟结果和观测值(图4)，结果显示ANN模型对潜热通量的模拟于30～120 W/m2的范围内模拟效果极好，超出该范围则误差显著增加，但变化趋势的一致性仍然较高，这与上文中ANN模型的折叠交叉验证结果相符.

图4 ANN模拟的潜热通量与观测值的对比Fig.4 Comparison between ANN estimated and observed latent heat flux

2.3 水热通量特征分析

2016年与2017年湖面通量数据的缺失状况较为一致(图5). 整个观测期内每天0:00-9:00是湖面通量数据时间覆盖率最低的时段. 通量源区定位取决于风速和风向，这表明该时间段内的主风向为陆地指向湖面. 与此相反，9:00-18:00时段湖面通量的时间覆盖率则远大于观测期平均水平. 上述现象表明观测地点存在显著的湖陆风循环.

经ANN模型插补，湖面通量于观测期间的变化特征得以清晰而完整地呈现(图5). 感热通量2016年与2017年的状况总体相似. 4-6月有着稳定而显著的日变化，每天的峰值多于10:00-16:00间出现，其中5月全段和6月上半月的日变化幅度较大. 从7月下旬起日变化减弱，但每天的整体强度显著增大. 10月下旬-11月底出现了持续一个月的高峰，且高峰期整体强度上2017年大于2016年. 高峰期过后迅速减小至7月前的水平.

图5 湖面通量插补前后对比：(a)感热通量，色标分辨率为2 W/m2；(b)潜热通量，色标分辨率为5 W/m2；(c)水汽通量，色标分辨率为0.1 mmol/(s·m2)(时间范围为2016年和2017年的4月3日-12月31日)Fig.5 Comparison between the unpatched and patched lake surface fluxes: (a) sensible heat, with a palette resolution of 2 W/m2; (b) latent heat, with a palette resolution of 5 W/m2; (c) molar water vapor, with a palette resolution of 0.1 mmol/(s·m2) (all included in the period of Apr. 3 and Dec. 31 in 2016 and 2017)

潜热通量最为显著的特征是日变化，每天的峰值于12:00-18:00间出现. 2016年和2017年的10-12月有着近两个月的高峰期. 与感热通量相反，2016年的潜热通量高峰期整体强度大于2017年. 由于观测期间气温变化幅度小于20℃，此幅度下温度变化对汽化潜热的影响低于3%，故水汽通量和潜热通量的强度变化几乎一致. 从两年的观测其整体状况来看，湖泊的能量释放于2016年4月初-10月末是一个渐强的过程，10月末达到顶峰. 而2017年的能力释放顶峰延后至11月下旬.

根据算法插补后的水汽通量数据及ANN的模拟误差期望，羊卓雍错湖面蒸发量的EC观测结果于4-12月为740±9 mm(2016年)和703±7 mm(2017年). 观测期湖面的感热通量平均值为14.9±0.2 W/m2(2016年)和14.3±0.2 W/m2(2017年)，潜热通量平均值为78.9±1.5 W/m2(2016年)和74.4±1.5 W/m2(2017年)，水面净辐射的平均值为126.7 W/m2(2016年)和139.5 W/m2(2017年). 由此可知湖面在2016年和2017年观测期间的能量平衡状况均为净流入，净流入能量为7.737×108J/m2(2016年)和1.198×109J/m2(2017年). 在不考虑湖水热力层结动态机制的情况下，净流入的热量可使湖面下方20 m深的湖水平均每月上升约1～1.5℃，在水体的垂直动态热平衡下，不同深度的水温变化可能各不相同.

3 结论与讨论

针对高寒湖泊涡动通量观测有效数据比例偏低的问题，本研究利用了近年来机器学习研究中GPU并行计算和算法优化方面的发展成果，通过基于信息利用原则的超宽ANN模型，有效优化了EC通量数据的连续性，并利用10次折叠交叉验证方法检验了ANN模拟的效果. 主要结论如下：

在ANN模型插补通量数据中有效地利用了同步观测特征信息与通量强度的热力、动力关联性. 从数据插补效果看，该方案揭示了湍流通量回归中跨量纲、跨维度映射拟合的可行性和有效性. 羊卓雍错湖面感热通量、潜热通量和水汽通量的有效观测平均值分别为18.8 W/m2、81.5 W/m2和1.84 mmol/(s·m2). 根据TensorFlow机器学习框架下超宽结构ANN模型交叉验证结果，模拟的AME分别仅有5.4 W/m2、15.7 W/m2和0.35 mmol/(s·m2). 10个交叉验证分组之间的误差波动幅度分别不超过1 W/m2、2 W/m2和0.05 mmol/(s·m2). 交叉验证组中全体观测值平均与模拟值平均的期望误差分别为2.0%、1.3%和1.8%. 这表明超宽ANN模型的通量模拟性能十分稳定，在各个交叉验证组中波动较小，且模拟误差具有较好的正负对称性.

高寒湖泊环境带来了湍流通量观测的缺测问题，通量数据插值是观测研究的必要部分. 湍流通量过程具有高复杂度、高非线性的特征，观测数据量大、种类多. ANN模型对输入数据的原始形态没有任何限制，无论所测同步观测数据的时间同步性、空间尺度、量纲、精度、采样率、噪声水平存在怎样的差别，都可以通过特征工程的标准化处理输入ANN. 超宽结构和GPU并行计算同时保证了ANN模型模拟通量时输入数据的充足和模型训练的时效，是ANN模型在通量数据插补问题上泛化的必要条件. 本研究对ANN模拟通量的验证分析表明，超宽ANN结构饱和输入同步观测要素的方式利用了更多有效信息. 本文将并行计算技术作为辅助工具引入通量观测研究之中，这显然是湍流通量观测研究所需进一步发展的方向. 基于大数据理论，通量模拟在数据量更大的区间效果更好，表明随着数据量增加通量模拟的效果还具备提升潜力. 本文验证ANN模型性能时发现，同步观测特征与通量强度通过超宽结构ANN模型完成了较好的映射关系拟合，这实现了同步观测特征变量自相关信息的有效利用. 因此，在今后的EC湍流通量观测实验中，通过增加同步观测要素，可以利用此插补方法改善高寒湖泊环境所带来的通量数据质量问题. 本文提出基于同步观测信息充分利用的数据插补思路为高寒湖泊等特殊环境下的EC通量观测实验提供了提升数据质量的参考.