基于运动模糊图像的数学模型建立与研究

张小圆 邓昌瑞 汪遥遥 吴国斌 聂水晶

（江西工程学院，江西 新余338000）

人们在使用相机进行拍照时，由于相机与被拍摄物之间存在相对运动，运动模糊图像的产生几乎是不可避免的，探讨在相对运动的状态下模糊图像产生的原因，进行机理分析并建立相应数学模型，为图像修复提供理论上的依据的工作就很有价值和必要。

1 本文涉及的几个重要符号说明

为探讨问题方便，做如下符号说明。

T：相机的曝光时间；

f（x，y）：没有受到噪声干扰下图像在点（x，y）处的像素灰度值，以下简称原图像；

ε（x，y）：在点（x，y）处图像所受到的噪声或干扰；

g（x，y）：受到噪声干扰图像在点（x，y）处的像素灰度值，以下简称模糊（退化）图像；

h（x，y）：在点（x，y）处的图像退化函数，以下称亦称点扩展函数；

F（u，v）：f（x，y）的傅立叶变换；G（u，v）：g（x，y）的傅立叶变换；

H（u，v）：h（x，y）的傅立叶变换，即运动模糊传递函数。

2 运动模糊图像产生的原因分析

要对由运动产生的模糊图像进行复原处理，首先要了解运动模糊图像的产生原因[1-3]。下面就被拍摄物在运动时所造成的模糊图像原因进行更深度的探讨。

为了研究方便，我们假设在拍摄时相机是静止的，而被拍摄物体是相对运动的。拍摄过程可以用如下示意图（见图1）进行描述：在位置A 处被拍摄物体以速度V1（t）在曝光期间（从拍摄的开始运动到拍摄结束）运动到A'，相对应地被拍摄物在相机靶面上移运动的速度为V2（t），且其影像则从a 运动到a'（这里假设AA'//aa'）。假设在拍摄过程中被拍摄物产生的位移为D，所对应在相机靶面上的影像位移变化为L，相机的曝光时间为T，相机的最大焦距为fmax。

在拍摄期间被拍摄物产生的位移为：

相机在曝光时间[0，T]内的平均速度为：

被拍摄物在靶面上产生的位移为：

被拍摄物在相机靶面上的平均速度为：

图1 拍摄运动情景模拟示意图

相机所拍摄出的图像实际上是在相机曝光期间所生成被拍摄物影像叠加而成的。由此可知，在相机的曝光期间，被拍摄物体由于运动产生了位置移动，造成被拍影像也变成其运动所产生的叠加图像，从而产生了由运动原因引起的模糊现象。

（1）当V1（t）=0 时，A 与A' 相重合，则此时相机所拍摄的图像最为清晰，此时曝光时间T 的变化，只会改变图像的亮度，而不会导致运动模糊；

（2）被拍摄物体移动速度V1（t）变化较快时，产生的图像就越模糊，此时曝光时间T 越大，图像的模糊程度就越严重破。

3 运动模糊图像数学模型的建立

要想对产生的运动模型图像进行修复还原，就要从更深层的角度对产生模糊的原因进行机理分析[4-5]，以建立出相应的数学模型，从而可以为图像复原做好理论依据。

3.1 图像的退化过程分析

模糊图像g（x，y）的形成，可以理解为是在拍摄过程中原图像f（x，y）的退化、外界噪声（或干扰）ε（x，y）所导致的，其图像退化过程可以描述如下（见图2）。

图2 图像退化过程示意图

由此，模糊图像的形成模型为：g（x，y）=f（x，y）*h（x，y）+ε（x，y）。

特别地，当ε（x，y）=0 时，有g（x，y）=f（x，y）*h（x，y）。

3.2 相对静止或匀速直线运动下模糊图像形成模型的建立

特别地，当被拍摄物体在拍摄期间做速度为V1（t）=V 的匀速直线运动时，显然有f（x，t）≡f（x）。

3.3 变速非直线运动下模糊图像形成模型的建立

在相机曝光时间内，物体不断地在做变速非直线运动的情况比较复杂的多，此时可假设在t 时刻，物体相对运动的运动分量为（x0（t），y0（t）），此时显然最终所得到的模糊图像为：

对上式g（x，y）做傅氏G（u，v）变化，有

3.4 两个重要参数的确定

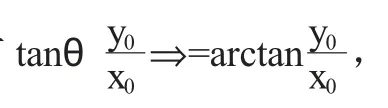
令a=x0（T）Lcosθ，b=y0（T）Lsinθ，可得到

再对G（u，v）=F（u，v）H（u，v）进行傅氏逆变换，即可把得到的g（x，y）还原成f（x，y）。

4 结论

运动是绝对的，用相机拍摄图像，不可避免的会因为相对运动而造成生成图像变模糊。但是只要我们能从实际出发，做到认真分析模糊图像产生的外在原因和进行科学的机理分析，总能并找到最佳解决的办法，能把生成的模糊图像最大限度地进行修复还原。