基于IPSO-Powell优化SVM的煤与瓦斯突出预测算法
吴雅琴, 李惠君, 徐丹妮
(中国矿业大学(北京)机电与信息工程学院,北京 100083)
0 引言
我国是世界上煤与瓦斯突出最严重的国家之一[1],对煤与瓦斯突出进行准确预测具有重大意义。随着计算机和仿真技术的发展,通过建立数学算法和计算机仿真与运算进行煤与瓦斯突出预测已成为当前煤与瓦斯突出预测的主要手段之一。刘俊娥等[2]建立了基于粗糙集-支持向量机(Rough Set-Support Vector Machine, RS-SVM)的煤与瓦斯突出风险判别模型,较单一使用支持向量机(SVM)模型具有更高的预测精度,但该模型缺少对核函数参数的优化,预测精度不高。孙玉峰等[3]应用SVM方法对煤与瓦斯涌出类型及涌出量进行了分析,并对核函数的判错率进行了研究,但在选择核函数时未考虑非线性数据的分类,对非线性分布的煤与瓦斯突出影响因素提取效果较差。杨力等[4]提出了基于模糊支持向量机(Fuzzy Support Vector Machine, FSVM)的煤与瓦斯突出预测模型,拥有比SVM更好的学习能力,但存在运算效率不高的问题。温廷新等[5]利用量子遗传算法对最小二乘支持向量机的参数作寻优处理,建立了煤与瓦斯突出预测模型,使预测结果避免了陷入局部最优解,但存在未成熟收敛的问题。周爱桃等[6]提出了基于支持向量分类机的煤与瓦斯突出危险性分类的预测方法,对比了4种核函数的预测能力,但缺少对主控因素的分析,运算的时间成本过大,可靠性不高。隆能增等[7]提出了基于局部线性嵌入法-果蝇优化算法-BP神经网络模型(LLE-FOA-BP)的煤与瓦斯突出强度预测方法,提高了算法的鲁棒性和学习效率,但数据量过大时模型存在训练速度较慢的问题。付华等[8]将等距映射算法与优化加权向量机耦合算法相结合,建立了煤与瓦斯突出双耦合算法预测模型,提高了煤与瓦斯突出的预测泛化能力,但缺少SVM模型的自身参数优化,无法满足算法的可靠性要求。
针对以上问题,本文提出了基于IPSO-Powell优化SVM的煤与瓦斯突出预测算法。首先通过灰色关联分析对煤与瓦斯突出的主控因素进行提取,消除了煤与瓦斯突出影响因素之间的冗余,并将其作为算法的输入样本;然后将改进的粒子群(Improved Particle Swarm Optimization,IPSO)算法与Powell算法结合起来优化SVM的惩罚系数和核函数参数[9],得到SVM的最优参数组合;最后将主控因素输入到SVM进行分类,并将其与实际测试集分类结果进行对比,实现煤与瓦斯突出预测。仿真结果验证了该算法的准确性和可靠性。
1 煤与瓦斯突出主控因素提取
根据煤与瓦斯突出机理的综合作用假说[10-12],影响煤与瓦斯突出的因素主要包括瓦斯含量、瓦斯压力、瓦斯放散初速度、煤的普氏系数、煤体破坏类型、软分层煤体厚度和开采深度等。为了研究不同影响因素对煤与瓦斯突出的影响程度,运用灰色关联分析理论,按照关联度的排序提取煤与瓦斯突出的主控因素,为煤与瓦斯突出预测算法的仿真实验奠定基础。
1.1 现场实例样本
通过收集整理相关文献所列山西屯兰矿、沙曲矿和寺河矿等矿井的样本数据[13-16],得到了119个现场实例样本,见表1。表1中煤与瓦斯突出强度为0的样本表示非突出样本,不为0的样本表示发生了煤与瓦斯突出的样本;煤体破坏类型分为5类,1—5分别表示非破坏煤、破坏煤、强烈破坏煤、粉粒煤和全粉煤。
1.2 灰色关联分析
灰色关联分析是对动态发展进程态势的量化剖析,运用灰色关联度的曲线图形来剖析系统因素间、因素对系统的影响水平的一种方式,通过确定参考数据列和剩余多个比较数据列的曲线图形的差异水平来判别其关系是否紧密,从而找到煤与瓦斯突出的主控因素。灰色关联分析计算步骤如下:
(1)确定参考数列和比较数列。假设煤与瓦斯突出有n个影响因素,对于m次突出案例,其突出强度的理想化样本如下:
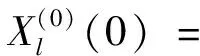
(l=1,2,…,m)
(1)
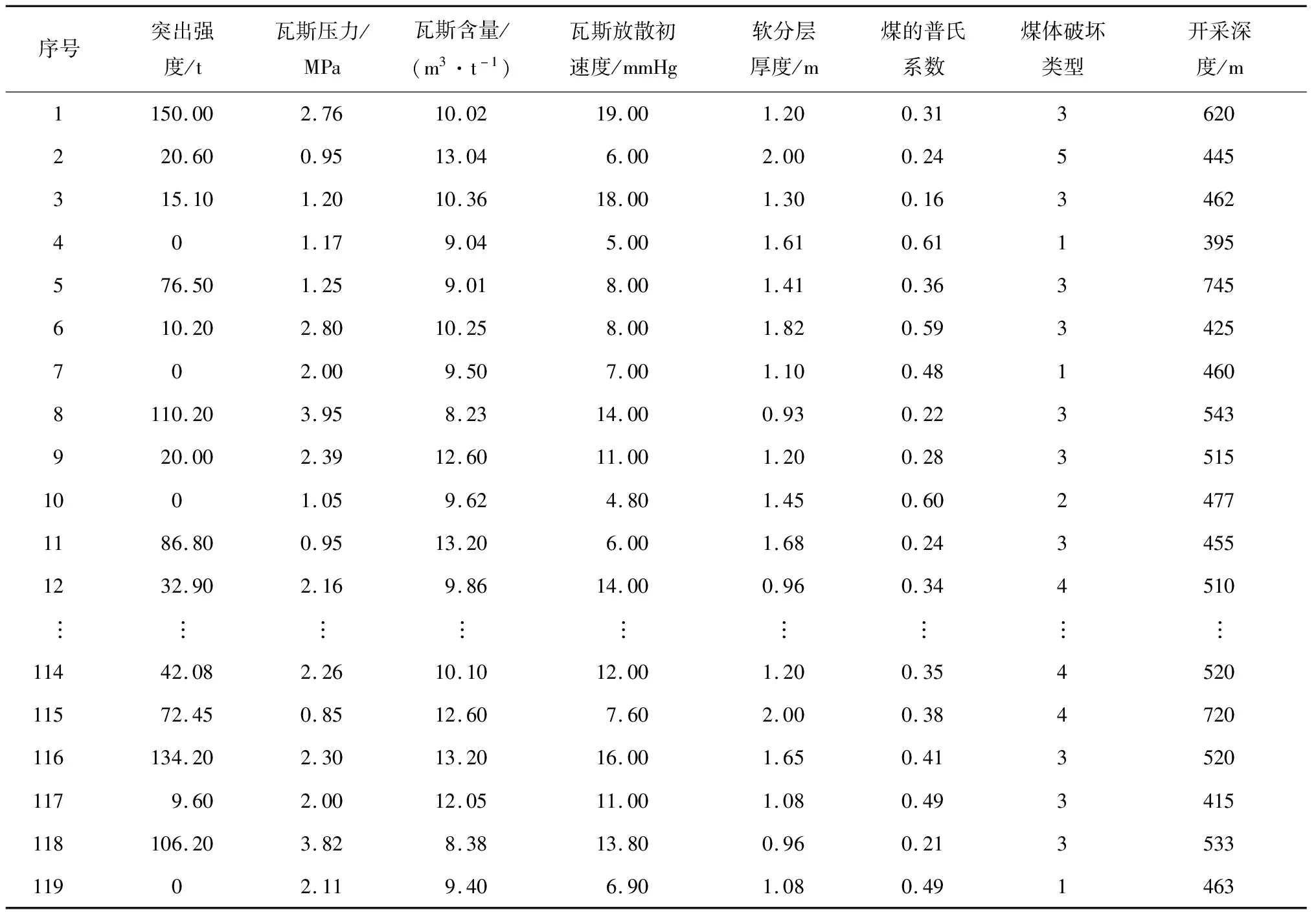
表1 现场实例样本
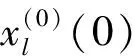
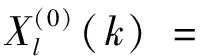
(k=0,1,…,n)
(2)

(2)变量无量纲化。由于各变量单位不统一、初值差异不方便对比,需要对数据进行标准化处理。
(3)
(3)计算关联系数η(k)。关联系数定义如下:
(4)
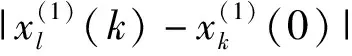
(4)计算各个突出影响因素的关联度。比较数列与参考数列在各个时刻的关联程度值为关联系数,计算出每一个突出影响因素和突出强度的关联系数后,采用式(5)计算结果作为比较数列与参考数列间关联程度的大小,关联系数的平均值称为关联度,反映数列之间的紧密程度。关联度r(k)的表达式为
(5)
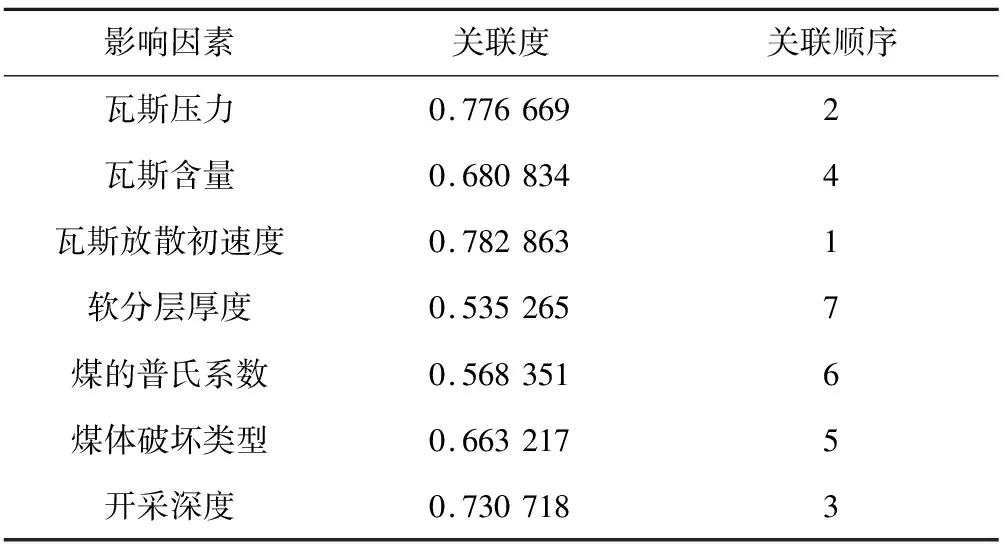
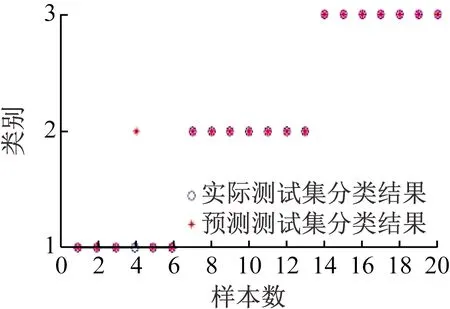
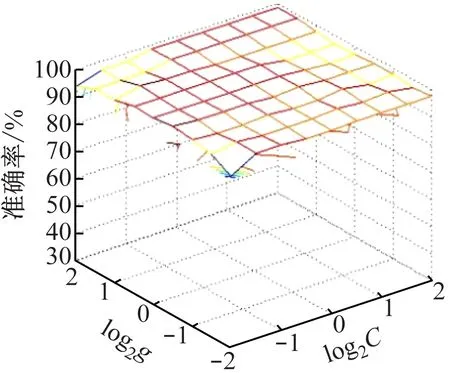
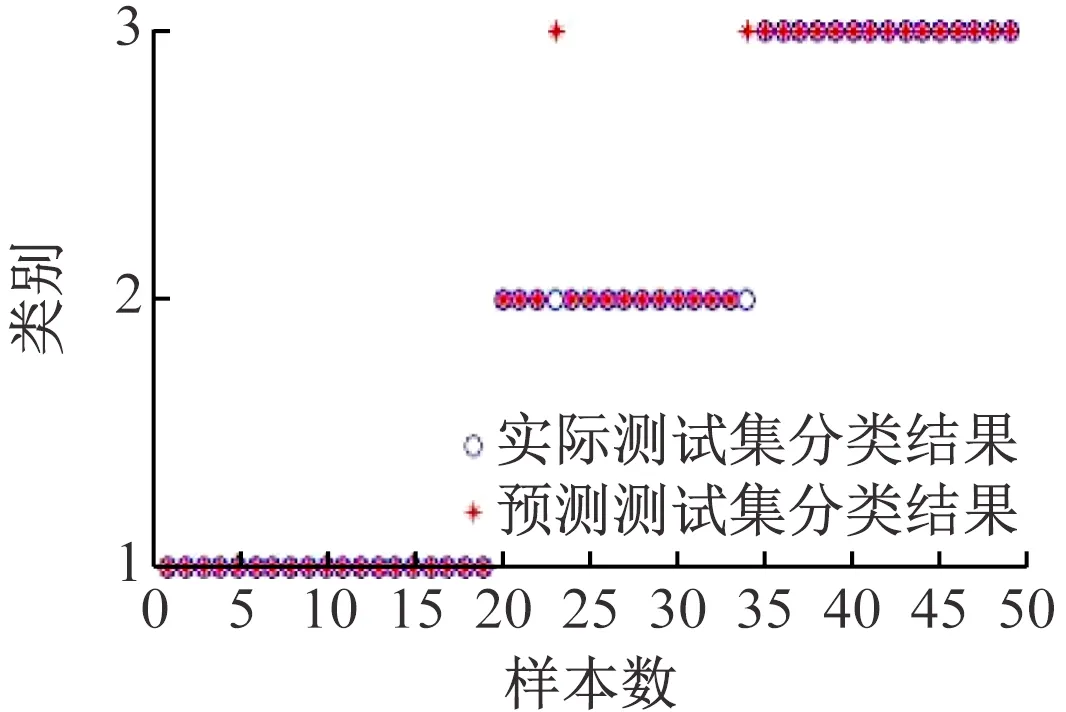
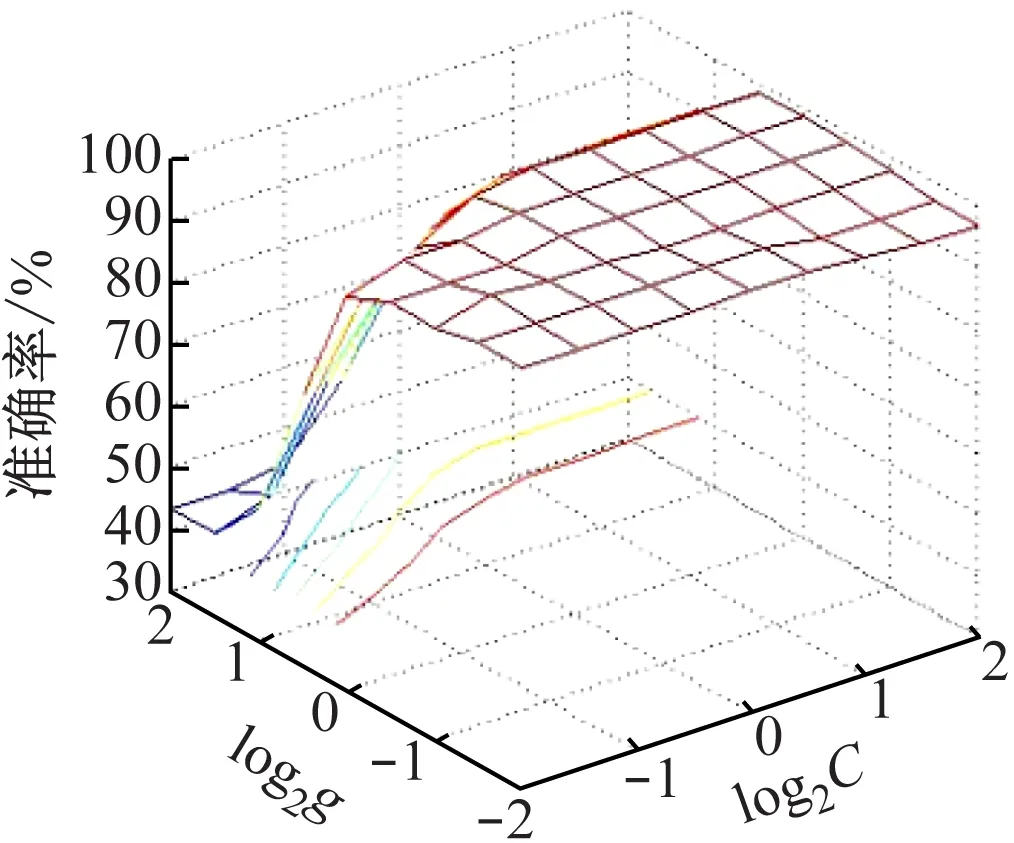
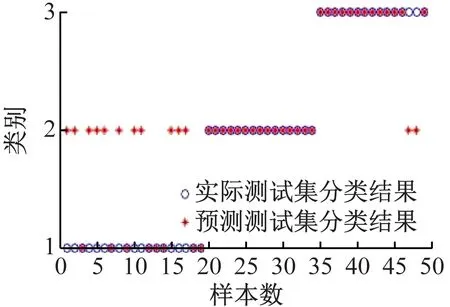
(5)关联度排序是按照关联度从大至小依次排列,假设r(1) 运用Matlab软件进行煤与瓦斯突出影响因素灰色关联分析,以突出强度为参考数列,以瓦斯含量、瓦斯压力、瓦斯放散初速度、煤的普氏系数、煤体破坏类型、软分层厚度和开采深度作为比较数列。对表1中发生突出的样本数据进行灰色关联分析,计算结果见表2。将关联度按照由大到小进行排序,关联顺序反映各个影响因素对煤与瓦斯突出的控制作用逐渐降低,从而提取煤与瓦斯突出的主控因素。各个影响因素对煤与瓦斯突出控制作用的顺序:瓦斯放散初速度>瓦斯压力>开采深度>瓦斯含量>煤体破坏类型>煤的普氏系数>软分层厚度,故提取瓦斯放散初速度、瓦斯压力、开采深度、瓦斯含量和煤体破坏类型作为煤与瓦斯突出主控因素。 表2 影响因素关联度排序 粒子群(Particle Swarm Optimization,PSO)算法利用群体中的个体对信息的共享来追随当前搜索到的最优值,从而找到问题求解空间中的全局最优解[17]。假设群体大小为z,目标搜寻空间为d维,Xi=(xi1,xi2,…,xid)T(i=1,2,…,z),表示第i个粒子的位置;Vi=(vi1,vi2,…,vid)T,表示第i个粒子的飞翔速度,粒子i自身搜索到的最好位置记为pbestid,gbestd为当前种群中粒子搜索到的最好的点,粒子i通过式(6)来迭代更新自身的速度与位置。 (6) 为使PSO算法在起初阶段搜索到足够大的范围,快速找到最优解的大概位置,以便后期进行局部精细搜索,利用IPSO算法,采用线性上升策略处理惯性权重。 (7) 式中:ωmax为权重最大值;Δω为权重最大值与最小值的差;tc,tmax分别为当前迭代次数和最大迭代次数。 将式(7)代入式(6)可得 (8) 用IPSO算法和Powell算法共同优化SVM的参数,并对PSO算法本身进行优化,然后结合Powell算法做进一步的局部寻优,反复迭代,将最后得到的最优解代入到SVM进行分类预测。IPSO-Powell优化SVM算法流程如图1所示。 图1 IPSO-Powell优化SVM算法流程 多项式核函数形式过于简单,非线性程度较低,高斯核函数很少发生维数灾难,并且超平面参数的个数较少,经综合考虑,本文采用高斯核函数作为SVM算法的核函数,其关键参数既可用σ表示,也可用g表示,两者之间的关系为 (9) 本文采用IPSO-Powell算法优化SVM算法中的2个参数,即惩罚系数C和核函数参数σ。算法运行步骤如下: (1)初始化参数:初始化IPSO算法的最大迭代次数tmax,学习因子c1、c2,混合算法的最大迭代次数M,Powell算法的搜索精度ε,搜索概率Pp等。 (2)利用适应度函数评价所有粒子的适应度。 (3)若混合算法的迭代次数大于M,则放弃迭代,将所有寻找到的极值点输出,否则继续下一步操作。 (4)若IPSO迭代代数t≤tmax,则更新粒子的位置、速度、pbestid和gbestd。 (5)r (6)将上述得到的极值点放入到极值点库中。 (7)再次初始化粒子的位置及速度。 (8)将极值点库中已经搜寻到的全局极值点赋给已初始化的粒子,返回步骤(3)。 (9)利用最优参数组合(C,σ)对SVM算法进行仿真实验。 为了分析不同比例的训练样本和预测样本对IPSO-Powell优化SVM算法结果的影响,利用流行的UCI数据库中的Wine数据集进行算法验证。Wine数据集中样本个数为178,属性个数为13,类别个数为3,分别记为1,2,3,随机选取4组训练样本和测试样本进行对比,具体结果见表3。 表3 实验数据对比 通过仿真实验将运算的预测测试集分类结果与实际测试集分类结果进行对比。4组测试样本的预测结果如图2—图5所示。从图2可看出,第1组89个样本中,有3个样本预测测试集分类结果为3,实际测试集分类结果为2,其余86个预测结果正确,准确率为96.6%。从图3可看出,第2组64个样本中,有2个样本预测测试集分类结果为3,实际测试集分类结果为2,其余62个预测结果正确,准确率为96.9%。从图4可看出,第3组41个样本中,有2个样本预测测试集分类结果为2,实际测试集分类结果为1,其余39个预测结果正确,准确率为95.1%。从图5可看出,第4组20个样本中,有1个样本预测测试集分类结果为2,实际测试集分类结果为1,其余19个预测结果正确,准确率为95%。4组预测结果准确率均超过95%。上述结果表明:选取不同比例的训练样本与预测样本对预测结果影响较小,准确率相差1%左右,基本符合算法预期效果。 图2 第1组测试样本的预测结果 图3 第2组测试样本的预测结果 图4 第3组测试样本的预测结果 图5 第4组测试样本的预测结果 (1)将运用灰色关联分析提取的煤与瓦斯突出主控因素(瓦斯放散初速度、瓦斯压力、开采深度、瓦斯含量和煤体破坏类型)作为算法的输入样本。 (2)利用IPSO-Powell优化SVM算法中的惩罚系数C和核函数参数σ,利用最优参数组合(C,σ)建立的SVM算法进行仿真实验。 (3)利用流行的UCI数据库中的Wine数据集分析不同比例的训练样本和预测样本对算法结果的影响,验证算法的可靠性。 (4)利用IPSO-Powell优化SVM算法计算预测测试集分类结果,并将其与实际测试集分类结果进行对比,对煤与瓦斯突出进行预测。 在表1所列119个现场实例样本中,随机选取70个作为训练样本,包括突出样本45个、非突出样本25个,另选49个作为预测样本。根据煤与瓦斯突出强度的大小把样本分成3类:无突出(标记为1)、小型突出(突出煤量为0~50 t,标记为2)、大型突出(突出煤量为50 t以上,标记为3),SVM模型的输出结果集用这个标准作为评价集。根据关联度计算结果从大到小进行排序,提取主控因素(瓦斯放散初速度、瓦斯压力、开采深度、瓦斯含量和煤体破坏类型)作为煤与瓦斯突出预测算法的输入样本进行仿真实验。 为分析基于IPSO-Powell优化SVM的煤与瓦斯突出预测算法的准确性和可靠性,将其与粒子群-支持向量机(Particle Swarm Optimization-Support Vector Machine,PSO-SVM)算法、遗传算法-支持向量机(Genetic Algorithm-Support Vector Machine,GA-SVM)算法和SVM算法进行仿真对比。 仿真时,要确定SVM算法中的惩罚系数C和核函数参数σ的值。如果C值太大,容易导致过拟合;如果C值太小,容易发生欠拟合。如果σ值太小,存在训练准确率很高而预测准确率不高的可能;如果σ值太大,则会出现平滑效应,无法实现较高的训练准确率,也会影响预测的准确率。首先对算法参数进行初始化,由IPSO算法和Powell算法根据适应度函数对SVM的惩罚系数C和核函数参数σ进行寻优,记录最优的一组参数组合(C,σ)进行仿真。 (1)利用IPSO-Powell优化SVM算法进行仿真,结果如图6所示。图6(a)中的g与参数σ的关系参见式(9)。当最优参数组合中C=0.329 88,σ=1时,49个样本中有2个样本预测测试集分类结果为3,实际测试集分类结果为2,其余47个预测结果正确,准确率为95.9%。 (a)算法参数和预测准确率关系 (b)预测结果 (2)利用PSO-SVM算法进行仿真,结果如图7所示。当最优参数组合中C=0.353 55,σ=0.5时,49个样本中有6个样本预测测试集分类结果为2,实际测试集分类结果为1,其余43个预测结果正确,准确率为87.8%。 (a)算法参数和预测准确率关系 (b)预测结果 (3)利用GA-SVM算法进行仿真,结果如图8所示。当最优参数组合中C=0.5,σ=1时,49个样本中有7个样本预测测试集分类结果为2,实际测试集分类结果为1,有2个样本预测测试集分类结果为2,实际测试集分类结果为3,其余 40 个预测结果正确,准确率为81.6%。 (4)利用SVM算法进行仿真,结果如图9所示。当最优参数组合中C=0.707 11,σ=0.25时,49个样本中有11个样本预测测试集分类结果为2,实际测试集分类结果为1,有2个样本预测测试集分类结果为2,实际测试集分类结果为3,其余36个预测结果正确,准确率为73.5%。 (a)算法参数和预测准确率关系 (b)预测结果 (a)算法参数和预测准确率关系 (b)预测结果 从仿真结果发现,IPSO-Powell优化SVM算法的预测准确率超过95%,其他3种算法的预测准确率均低于90%,说明IPSO-Powell优化SVM算法在迭代次数较少的情况下预测准确率更高。 (1)运用灰色关联理论分析各个影响因素对煤与瓦斯突出的影响程度,根据关联度的排序提取瓦斯放散初速度、瓦斯压力、开采深度、瓦斯含量和煤体破坏类型作为煤与瓦斯突出主控因素。 (2)将IPSO算法与Powell算法相结合对SVM算法的惩罚系数C和高斯核函数参数σ进行寻优。运用IPSO-Powell优化SVM算法对不同比例训练样本与预测样本的仿真结果进行预测,预测准确率均超过95%,表明选取不同比例的训练样本与预测样本对预测结果影响较小。 (3)在提取煤与瓦斯突出主控因素的基础上,构建了基于IPSO-Powell优化SVM的煤与瓦斯突出预测算法。IPSO-Powell优化SVM算法和SVM算法、GA-SVM算法、PSO-SVM算法的仿真对比结果表明:基于IPSO-Powell优化SVM的煤与瓦斯突出预测算法具有更高的预测精度,同时提高了SVM 求解过程的运算效率,为煤与瓦斯突出预测提供了新的思路和方法。1.3 煤与瓦斯突出影响因素灰色关联度排序
2 IPSO-Powell优化SVM的煤与瓦斯突出预测算法
2.1 算法原理
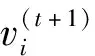
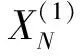

2.2 不同比例样本对算法结果的影响
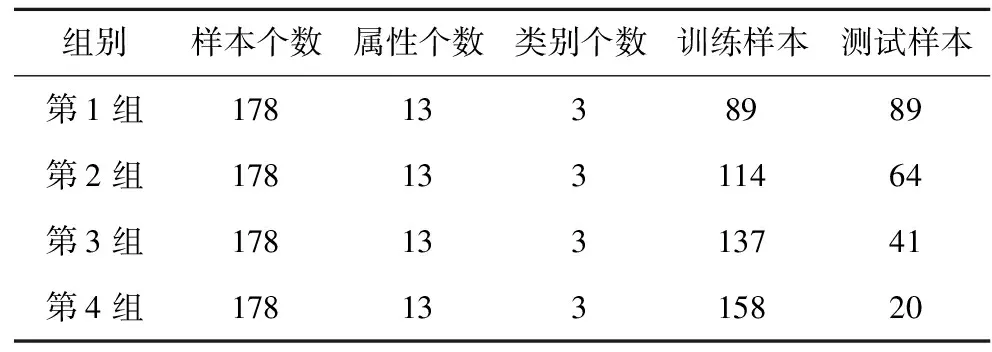
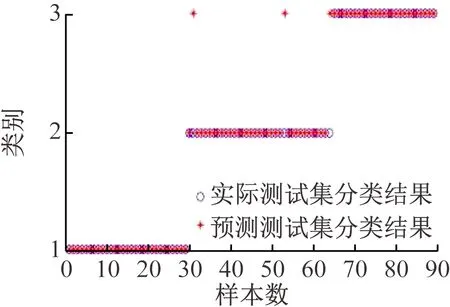
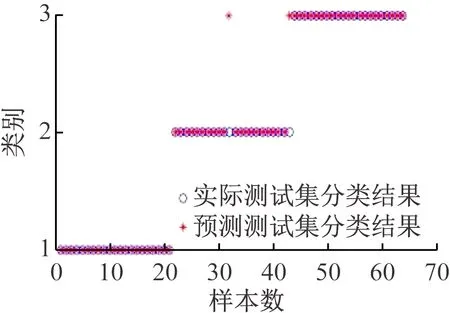
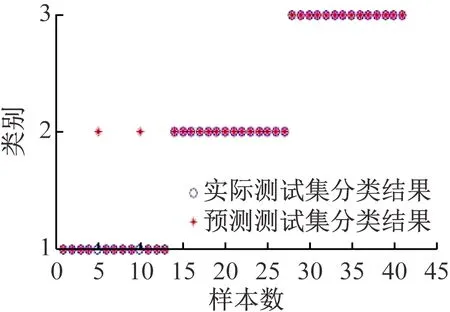
2.3 煤与瓦斯突出预测步骤
3 算法仿真
3.1 数据样本的处理
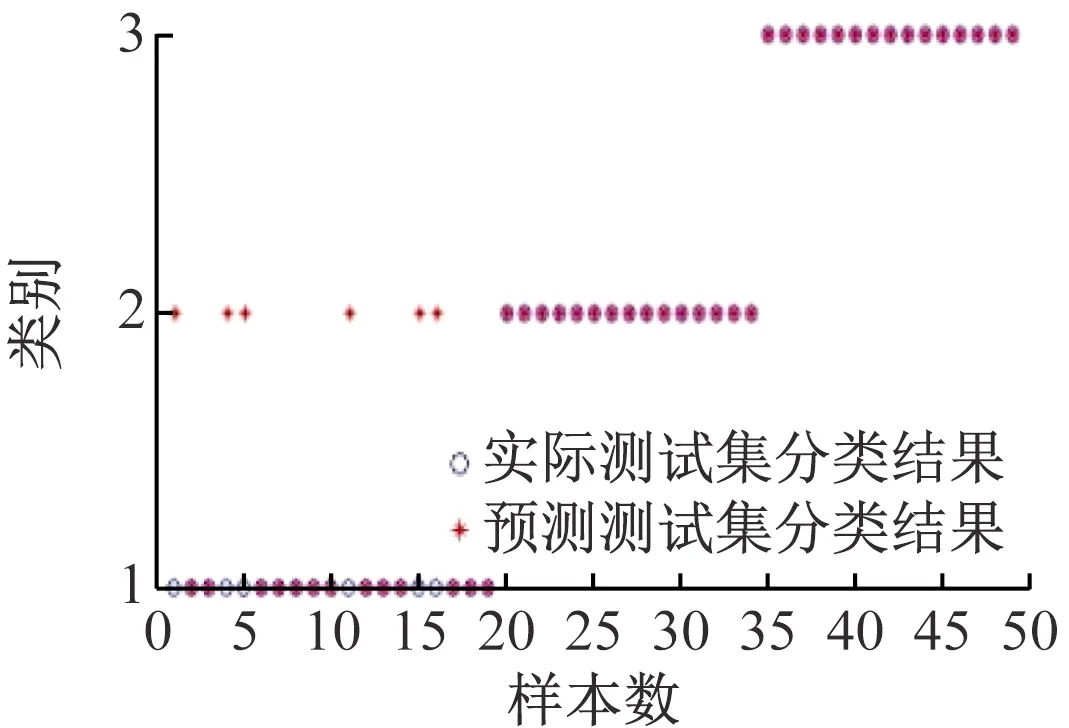
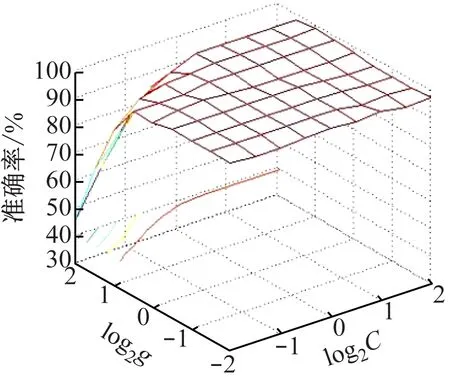
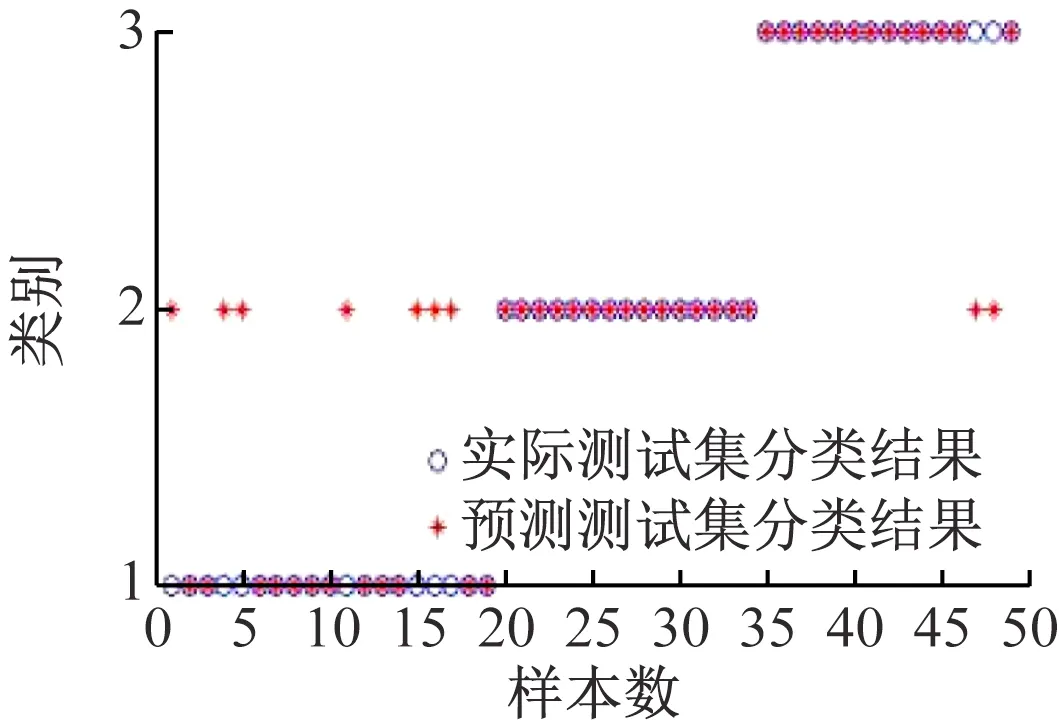
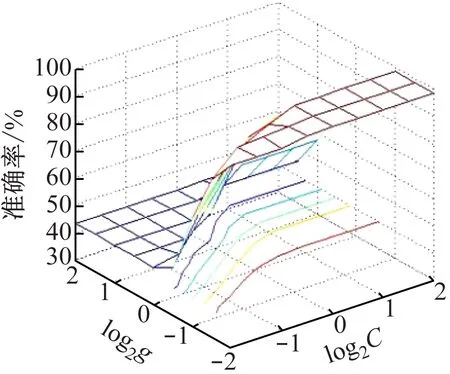
3.2 不同算法仿真结果对比
4 结论

