我国西南地区支线机场旅客吞吐量与地区GDP的关系分析

刘 静， 朱志愚， 任志强， 李 涛

(中国民用航空飞行学院， 四川 广汉 618300)

随着近年来支线航空的快速发展，支线机场作为保障支线航空运输服务的基础设施，在航空运输网络中起到重要的支撑作用。《民用航空支线机场建设标准》(MH5023—2006)中对支线机场的界定为：目标年旅客吞吐量小于50万人次(含)或主要起降短程飞机或直达航班在800～1 500公里范围内[1]。西南地区由于长期受地理区位和地形条件的限制，地面运输基础设施落后。西部大开发战略实施20年来，航空运输业在西南地区快速发展，各省市均加快支线机场建设。截至2018年底，西南地区拥有42个支线机场，成为我国支线机场最多的地区[2]。由于目前西南地区大部分支线机场都处于亏损运营状态，支线航空运输发展缓慢、一波三折，支线机场与区域经济发展的关系，成为业界和地方政府普遍关心和需要进一步深入研究的问题。

1 国内外研究现状

国内学者对民航运输机场和区域经济发展关系做了一些研究。如宋怀祖通过分析复合大型枢纽机场建设与区域经济互动发展的关系，指出区域经济的发展有助于优化航线网络布局、提高机场利用率、促进机场的整合、推动大型枢纽机场建设[3]。张国伍以首都机场为例，分别测算出首都机场对全国和北京市产生的经济效益，提出了推动机场和区域经济协调发展的建议[4]。郑燕琴探究了白云机场和花都区经济发展的关系，发现关联度较高并说明不同规模的机场和区域经济关系的差异[5]。

综上，国内研究成果大多对省会枢纽和干线机场与区域经济发展的关系进行研究，对支线机场与区域经济发展关系的研究还很少。国外研究主要关注支线机场发展对地区就业水平、产业结构转变、机场收入等的作用。本文试图运用协整理论中的平稳性检验、协整检验和误差修正模型，通过分析机场旅客吞吐量和区域GDP的关系，从长期弹性和短期弹性的视角，揭示我国西南地区支线机场与区域经济发展的关系。

2 西南地区支线机场旅客吞吐量与GDP协整关系研究

2.1 研究对象

基于数据的可获得性，从民航生产统计公报、各省统计局收集数据，以1998—2018年西南地区42个支线机场(表1)的年旅客吞吐量总和(表示为TQ)作为西南地区支线机场发展情况指标；以1998—2018年四川省、云南省、贵州省、重庆市、西藏自治区的年GDP总和作为西南地区经济发展的指标。

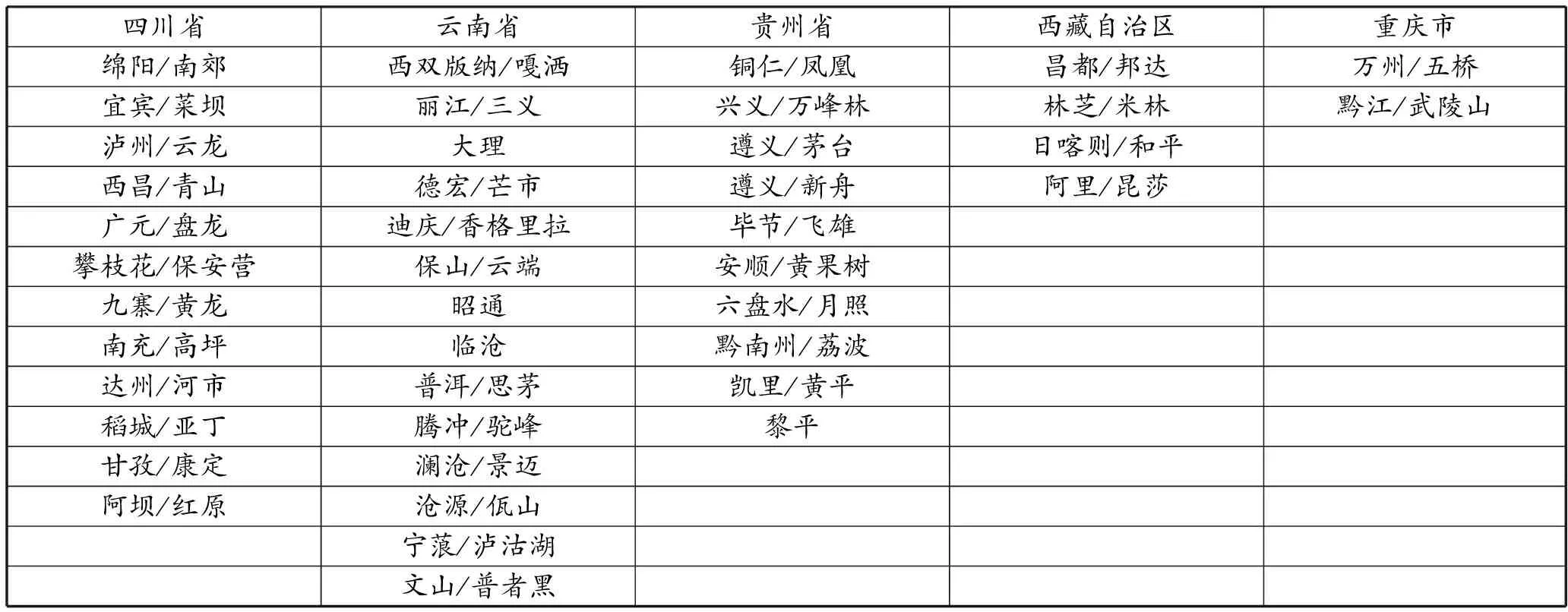
表1 西南地区42个支线机场名称表

2.2 数据处理

为了保证研究的科学性与合理性，对所收集的数据做如下处理。

1)为反映各地区经济发展实际状况，消除物价和通货膨胀对GDP的影响，用各省份当年的GDP除以居民消费价格指数获得不变价格GDP。

2)对TQ与不变价格GDP总和(表示为GDP)取对数，以消除时间序列数据的异方差影响，使时间序列数据具有良好的统计性质，增强序列的稳定性，同时不会影响各时间序列之间的协整关系。计算后的数据见表2。

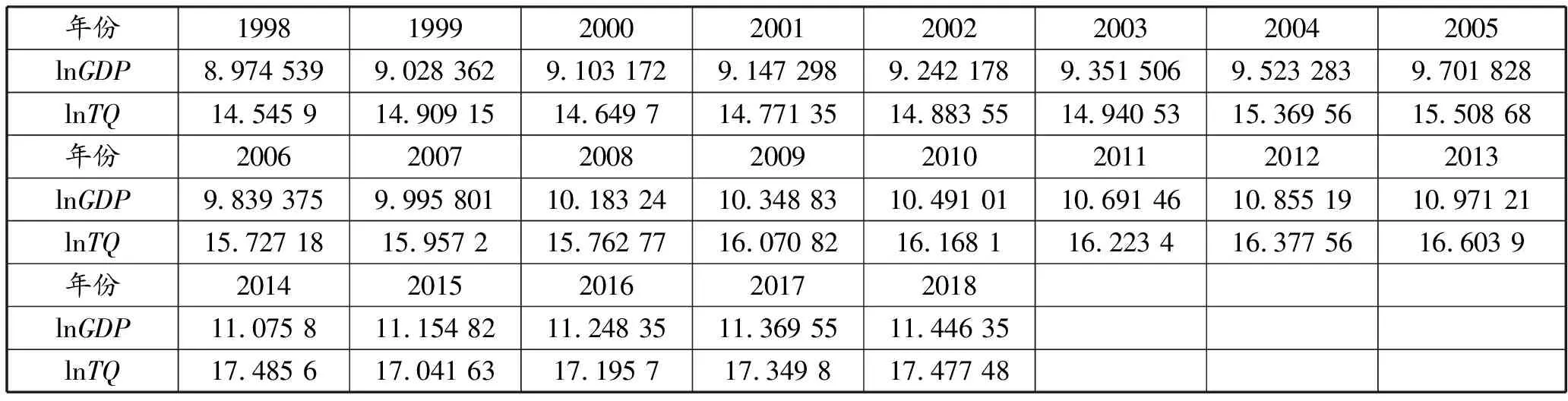
表2 lnGDP和lnTQ数据表

2.3 平稳性检验

时间序列的平稳性是指时间序列的统计规律不随时间推移而发生变化，在图像上表现为一条围绕其均值上下波动的曲线[8]。图1中lnTQ和lnGDP都呈现了明显的增长趋势，是具有上升趋势的时间序列而非平稳序列。为了满足后续协整检验的要求，首先要对其进行平稳性检验，否则直接对非平稳时间序列进行协整检验则可能造成虚假回归。协整检验要求非平稳时间序列必须为同阶单整，即几个时间序列变量经过n阶差分后变成平稳序列，则称为n阶单整[9]。

通常采用ADF检验法进行平稳性检验，其原假设是：至少存在一个单位根，即时间序列不平稳；备择假设是：不存在单位根，即时间序列平稳。下面对lnTQ和lnGDP进行ADF检验，结果如表3。本文所有计算均采用Eviews9.0完成。

表3显示，ΔlnGDP、ΔlnTQ的统计量t均小于对应的5%临界值，拒绝原假设，表明ΔlnGDP、ΔlnTQ为平稳序列，故lnGDP、lnTQ都为一阶单整时间序列，可以进行协整检验。

表3 变量平稳性检验结果

注：①lnGDP和lnTQ表示一阶差分序列；②**代表5%显著水平下所对应的平稳性。

图1 支线机场旅客吞吐量与GDP趋势图

2.4 协整检验

协整检验是检验变量之间长期均衡关系的一种方法，也是区别真实回归和虚假回归的有效方法。由2.3可知lnGDP、lnTQ均为一阶单整时间序列，可以对其进行协整检验。协整检验方法主要有基于回归系数的协整检验和基于回归残差的协整检验[10]。因本文是两个变量的协整检验，故采用Engle和Granger提出的基于回归残差的协整检验方法即EG两步法，先建立协整回归方程，再对回归方程的残差进行ADF检验。

第一步用最小二乘法(OLS)建立协整回归方程，将表2中的数据输入Eviews9.0软件，计算得到：

lnTQ=4.63545+1.11197lnGDP+εt1

(1)

(8.524396) (20.88356)

R2=0.958253， DW=1.734820

lnGDP=-3.56976+0.861765lnTQ+εt2

(2)

(-5.412914) (20.88356)

R2=0.958253， DW=1.664153

注:括号内数字为解释变量显著性水平，即t统计量；R2为判定系数，取值在0和1之间，值越接近1，说明回归方程对样本观测值的拟合程度越高；DW为自相关检验统计量，DW统计量在2附近说明序列无自相关性，即时间序列中的不同时间点的样本无显著相关性，满足最小二乘法回归的假设前提。

上述方程的判定系数为0.958 253，表明模型的拟合情况非常好，DW值均在2附近，说明变量序列无自相关性，即lnGDP、lnTQ时间序列中不同时间点的样本无显著相关性。

由公式(1)、(2)得到残差方程(3)、(4)：

εt1=lnTQ-4.63545-1.11197lnGDP

(3)

εt2=lnGDP+3.56976-0.861765lnTQ

(4)

第二步，对残差εt1和εt2进行ADF检验，检验结果如表4。

表4 残差εt1、εt2 ADF检验结果

对残差进行ADF检验时，Eviews给出的统计量t不能用来衡量检验结果的显著性，即不能确定残差是否平稳，需根据临界值公式计算出的统计量C值进行判断[11]。

根据临界值计算公式(5)和协整回归临界值表5计算出实际统计量C，见表4。

C(a)=Ø+Ø1T-1+Ø2T-2

(5)

表5 部分协整回归临界值表

注：表中的常数项、趋势项指残差方程中是否含有常数项、趋势项；N为参数个数，包含解释变量与被解释变量。

临界值C(εt1)=-3.6422>t-统计量=-3.829797，拒绝原假设，残差εt1具有平稳性。同理， C(εt2)拒绝原假设，残差εt2具有平稳性。

由残差εt1和εt2均具有平稳性，可以判断lnGDP和lnTQ存在协整关系。协整回归方程(1)显示， lnGDP的系数为1.111 97，即TQ对GDP的长期弹性为1.111 97。长期来看，GDP增加1%，TQ将增加1.111 97%。协整回归方程(2)显示，lnTQ的系数为0.861 765，即GDP对TQ的长期弹性为0.861 765。长期来看，TQ增加1%，GDP将增加0.861 765%。

方程(1)、(2)表明，TQ与GDP之间存在着长期稳定的比例关系，即TQ和GDP具有长期均衡和协同发展关系。

2.5 建立误差修正模型(Error Correction Model，ECM)

协整检验结果表明TQ与GDP间存在长期稳定的关系，但这种长期稳定关系是在不断的短期调整下得以维持的。下面建立TQ与GDP的误差修正模型，对变量间的短期波动情况进行分析。具体公式如下[12]：

ΔYt=β1ΔXt+λ*ECM+εt

(6)

式(6)中，ECM为误差修正项；λ为误差修正系数，表示当期解释变量的变动对上一期的非均衡修正程度，当系数为负值时表明存在误差修正机制，即GDP和TQ的长期均衡值对短期偏离的修正力度；β1为短期弹性系数，反映因变量ΔYt与自变量ΔXt的短期关系；εt为时间趋势项。

误差修正模型的关键在于最优滞后阶数的选择，即因变量受到解释变量前期值的影响时间。本文采用多准则联合确定法，根据Eviews给出的判定依据表结果，综合考虑滞后期长度和自由度，选取AIC(Akaike information criterion)、FPE(Final prediction error)、HQ(Hannan-Quinn information criterion)信息准则确定的2阶最优滞后阶数(表6)。

表6 模型滞后阶数的判定依据

注：*indicates lag order selected by the criterion。

建立ECM模型如下：

ΔlnTQt=-0.895256ECM1,t-1-0.000300ΔlnTQt-1-0.290160ΔlnGDPt-1+0.171795

(7)

(-0.00125) (-0.23706)

其中，ECM1,t-1=lnTQt-1-4.63545-1.11197lnGDPt-1

ΔlnGDPt=-0.027135ECM2,t-1+0.703818ΔlnGDPt-1-0.014007ΔlnTQt-1+0.040611

(8)

(3.50746) (-0.35665)

其中，ECM2,t-1=lnGDPt-1+3.56976-0.861765lnTQt-1

注：ΔlnTQt-1、ΔlnGDPt-1分别为lnTQt-1、lnGDPt-1的一阶差分；括号内的数字为t统计量。

公式(7)结果显示，TQ对GDP的短期弹性为0.290 160，说明从短期来看，GDP增加1%，TQ增加0.290 160%；误差修正项ECM的系数为-0.895 256，说明当上一年TQ偏离长期均衡时，为了保持TQ与GDP的长期均衡关系，当年TQ的变化值可以修正上一年89.53%的非均衡误差，反映出这两者的长期均衡关系对TQ的短期波动有较强的调整力度。同样，公式(8)结果显示，GDP对TQ的短期弹性为0.014 007，即从短期来看，TQ增加1%，GDP将增加0.014 007%；误差修正项ECM的系数为-0.027 135，说明当上一年GDP偏离长期均衡时，为了保持GDP与TQ的长期均衡关系，当年GDP的变化值可以修正上一年2.71%的非均衡误差，调整力度较小。

3 结论

本文基于协整理论方法，探究了西南地区支线机场旅客吞吐量与地区GDP间的关系，分析结果如表7。

表7 西南地区机支线场旅客吞吐量与GDP弹性系数、误差修正系数表

表7的数据显示：

1)TQ与GDP之间不论长期还是短期都存在正向比例关系。当TQ和GDP出现短期波动偏离均衡状态时，会产生一种反馈机制进行修正，误差修正项将分别以0.895 256和0.027 135的力度从短期非均衡状态向长期均衡状态拉近。无论二者在短期内如何波动，长期仍会趋向均衡状态，呈现出协同发展的状态，但GDP偏离长期均衡时的修正力度小，TQ偏离长期均衡时的修正力度大。

2)GDP对TQ的弹性无论长期和短期均小于TQ对GDP的弹性，GDP对TQ和TQ对GDP的弹性均表现为长期弹性大于短期弹性。

上述特点表明，西南地区GDP和支线机场发展存在以GDP为主的协同作用，协同发展状态长期比短期更明显。协同作用的提高，需要长期的市场培养、政府扶持和地区产业结构调整的支撑。随着西南地区产业结构的优化升级，高新技术产业和旅游服务业比重的增加，其社会经济发展对航空运输的需求会越来越大，支线机场旅客吞吐量与地区GDP的关联作用和协同发展态势会逐渐增强。在我国建设民航强国的进程中，支线航空的发展是一个重要的环节和基础，需要兼顾局部利益和全局利益、长期利益和短期利益，制定符合国情的支线航空长期发展战略和政策措施，有效促进支线航空的发展。