温习“外延”而知“周延”

张康伟

摘 要：直言命题主谓项的周延性问题是关于直言命题中主项与谓项量的问题，分为周延与不周延。在此，为了帮助逻辑学初学者和爱好者更加清楚明了地认识和掌握直言命题主谓项的周延性问题，笔者主要是通过让大家温习外延知识，结合欧拉图学习周延性问题。说清楚这个问题，对于正确理解各类词项逻辑形式的含义和特性，以及进行相关的推理具有重要意义。

关键词：直言命题;外延;欧拉图; 周延

关于“周延性”这一概念，主要是逻辑学家针对于传统词项逻辑中的A、E、I、O四种直言命题所提出的，“用于衡量四种直言命题的主项与谓项的外延中的个体是否被全部断定。如果词项外延中的个体在一个直言命题中被全部断定，那么它在该命题中是周延的;否则，它不是周延的。”[1]

本文试图通过对易懂概念词项外延的认识，结合欧拉图来浅析直言命題主谓项的周延性问题。那什么是“外延”呢？在传统词项逻辑中词项具有内涵和外延两个特性，而词项的外延就是指该词项所指称对象的范围，例如，“人”这个词项的外延就是指古今中外，不同国家、不同性别、不同年龄的所有人。知道什么是外延，那 “欧拉图”又是什么呢？在18世纪，瑞士数学家欧拉（1707-1783）创造了一种用圆圈表示词项间外延关系的图解法，后来人们称这种图解法为欧拉图。这种图解法可以形象直观地刻画直言命题中两个词项外延之间的关系，例如全同关系、真包含关系、真包含于关系、交叉关系和全异关系。借助欧拉图对直言命题中两个词项的外延关系的分析，可以帮助我们更加深刻地掌握直言命题主谓项周延性问题。

直言命题从词项外延的角度来看，其主要表达词项外延之间的关系，由量项、主项、联项和谓项组成。量项规定被谈论事物的量，主项代表所谈论事物的词项，联项的作用是联结主项和谓项，谓项表达所谈论事物的性质，按联项和量项的结合来划分， 可以分为全称肯定直言命题、全称否定直言命题、特称肯定直言命题、特称否定直言命题四种基本类型。

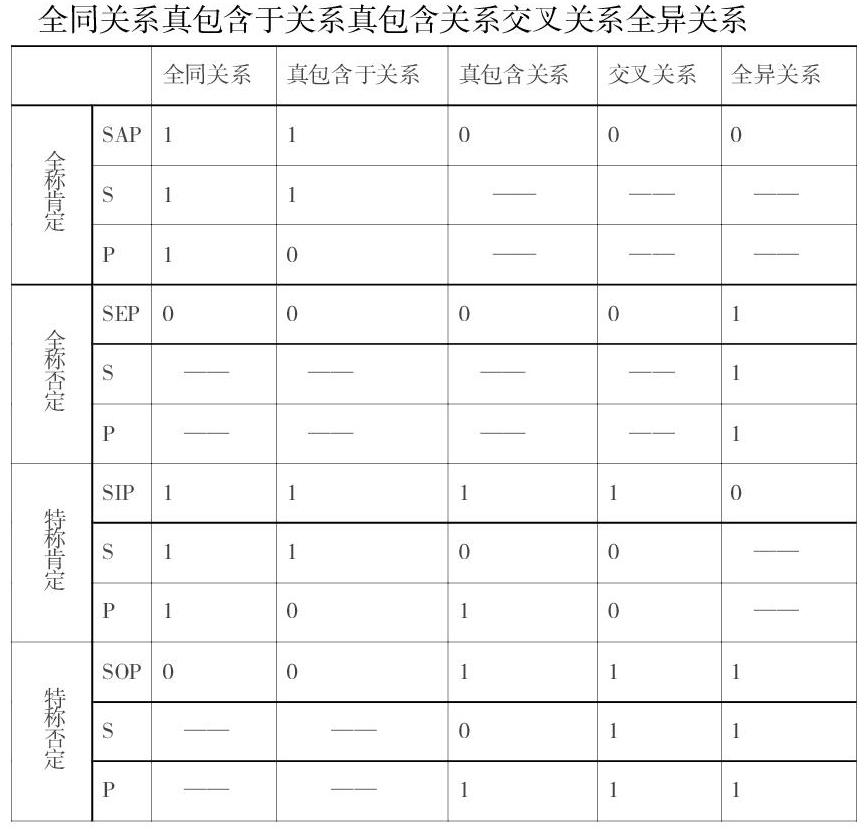
我们可以借助欧拉图分别刻画词项S与词项P之间的全同关系、真包含于关系、真包含关系、交叉关系和全异关系。

如下图所示：

接下来我将借助欧拉图对四种基本的直言命题逐一进行探讨。

（一）全称肯定直言命题

全称肯定直言命题（形式结构是“所有S都是P”，记作SAP，对于一个具体的全称肯定命题，如果它是真的，则该命题所断定的主、谓项外延间的关系不外乎有两种情况：即主项（S）和谓项（P）之间或者是全同关系，或者是真包含于关系。

（1）全称肯定直言命题的主项（S）的周延情况

结合以上的欧拉图分析一下全称肯定直言命题的主项（S）的周延情况，如果主项（S）周延，S外延中的所有个体都被断定，也就是说在欧拉图中所有S都与整个或部分P重合。

①全同关系

在全同关系中如图一所示：S外延中的所有个体与整个P重合，S外延中的个体被全部断定，所以全称肯定直言命题的主项（S）在全同关系中是周延的。在传统词项逻辑中用简洁的语句明确词项内涵的逻辑方法——定义，它的定义项（Dp）与被定义项（Dp）正是要符合全称肯定直言命题中的全同关系的要求。

②真包含于关系

在真包含于关系中即图二所示：所有S与部分P完全重合，与S完全重合的这部分P确定地断定了S外延中的全部个体，所以全称肯定直言命题的主项（S）在真包含于关系中是周延的。

主项（S）在全称肯定直言命题所断定的主、谓项的外延间的关系即全同关系和真包含于关系中都是周延的，可以给出一个肯定的结论：全称肯定直言命题的主项（S）是周延的。

（2）全称肯定直言命题的谓项（P）的周延情况

结合欧拉图再看一下全称肯定直言命题的谓项（P）的周延情况，如果谓项（P）周延，等价地说就是P外延中的所有个体都被确定地断定，也就是说在欧拉图中整个或部分S与P完全重合。

①全同关系

在全同关系中即图一所示：整个S与P完全重合，也就是说，我们通过整个个S可以确定地断定P外延中的所有个体，所以全称肯定直言命题的谓项（P）在全同关系中是周延的。

②真包含于关系

在真包含于关系中即图二所示：整个S只与部分P重合，没有与所有P重合，也就是说在真包含于关系即图二中只断定了P外延中与S有重合的 部分外延中的个体，没有确定地断定P外延中的所有个体，因此全称肯定直言命题的谓项（P）在真包含于关系中是不周延的。

只有当谓项（P）在全同关系和真包含于关系中都周延，才可以说全称肯定直言命题的谓项（P）是周延的，因为P在真包含于关系中不周延，所以说全称肯定直言命题的谓项（P）是不周延的。

（二）全称否定直言命题

全称否定直言命题（形式结构是“所有S都不是P”，记作SEP，对于一个具体的全称否定直言命题而言，如果它是真的，则该命题所断定的主、谓项的外延间的关系只有一种情况：主项（S）和谓项（P）之间是全异关系。

（1）全称否定直言命题的主项（S）的周延情况

结合以上的欧拉图分析一下全称否定直言命题的主项（S）的周延情况，如果主项（S）周延，等价地说就是S外延中的所有个体都被断定，也就是说在欧拉图中所有S与整个或部分P没有重合。在全异关系中即图五所示：所有S外延中的个体与整个或部分P没有任何重合，由此可知全称否定直言命题的主项（S）在全同关系中是周延的。

（2）全称否定直言命题的谓项（P）的周延情况

再结合欧拉图分析一下全称否定直言命题的谓项（P）的周延情况，如果谓项（P）周延，等价地说就是P外延中的所有个体都被断定，也就是说在欧拉图中整个或部分S与P外延中的个体没有任何重合。在全异关系中如图五所示：整个S与所有P没有重合，可以看出来全称否定直言命题的谓项（P）在全异关系中是周延的。