资金等值计算公式研究综述
王运鑫


【摘 要】资金等值在经济活动系统中应用广泛,资金时间价值的各参数在不同情况下计算公式相似却不同。针对等值计算公式的易混淆性,论文从间歇现金流间断复利、间歇现金流连续复利及连续现金流连续复利三方面综述了等值计算的研究现状,总结了各情况下的等值计算公式,有利于区分、记忆等值计算公式。最后,论文提出连续现金流连续复利的等值计算更符合实际,应推广应用。
【Abstract】Capital equivalent is widely used in economic activity system. The calculation formulas of parameters of the time value of capital are similar but different in different cases. In view of the confusion of equivalent calculation formulas, this paper summarizes the research status quo of equivalent calculation from three aspects: intermittent compound interest of intermittent cash flow, continuous compound interest of intermittent cash flow and continuous compound interest of continuous cash flow, summarizes the equivalent calculation formulas in each case, which is conducive to distinguish and memorize the equivalent calculation formulas. Finally, the paper proposes that the equivalent calculation of continuous compound interest of continuous cash flow is more practical and should be popularized and applied.
【关键词】资金等值;等值计算;间断复利;连续复利
1 引言
资金等值是指在考虑资金时间价值的情况下,不同时点上数额不等的资金在一定利率条件下可能具有相等的价值[1]。等值计算即把某一时间点上的资金值换算为另一时间点上价值相等但数值不等资金值的过程。资金等值计算可解决不同时间点的资金的可比性问题和正确评价由于时间因素产生的经济效果,其广泛应用于多方案评价、优选中。在CNKI文献搜索平台上,以“资金等值”为主题的文献仅有十篇左右,其主要集中于间断复利的一次支付、等额分付六个基本公式的等值计算研究,并且研究年份都比较早。近年来,国内学者倾向于对间断现金流连续复利、连续现金流连续复利的计算与应用研究。本文从间歇现金流间断复利、连续复利及连续现金流连续复利三方面阐述了具体研究现状及等值计算公式,为今后资金等值的研究提供方向。
2 资金等值计算的研究现状
国内资金等值计算研究起步于20世纪80年代末,最初的研究以介绍资金时间价值和一次支付、等额分付的等值计算基本公式为主。例如,1987年,石璞[2,3]首次对资金时间价值和等值基本计算做出了简单介绍;1994年,韩卫涛[4]对复利制下等值计算的六个公式进行了算例分析;2003年,郭秀英等[5]将等值基本计算应用于投资项目经济评价中;2007年曾波[6]提出资金等值计算可改进传统按揭购房还贷。之后的研究重点开始向等差、等比现金流序列的等值计算及连续复利情况下等值计算转移,以便于分析计算特殊现金流序列和连续复利的工程经济问题。例如,2009年,沈浩[7]列出了等差、等比序列等值计算的示意图及计算公式推导过程;2009年,刘万鹏等[8]通过比较间断复利和连续复利的不同,研究了等比现金流序列连续复利对资金时间价值的影响;2014年,杨卫军等[9]将递减等比、等差序列的间断现金流连续复利计算公式应用到垫资承包工程中,得出连续复利计算资金时间价值较合理的结论。近年来,学者开始重视对连续现金流连续复利进行研究。例如,2015年,吴宏亮等[10]建立了连续现金流连续复利计算模型,并应用于设备维护费用现金流的计算案例中,提出运用该模型可提高计算结果的准确性;2016年,杨瑾[11]用数学方法推导出连续现金流连续复利的计算公式,并在算例分析中对比了间断现金流间断复利、间断现金流连续复利和连续现金流连续复利三种情况下的计算结果,提出连续现金流连续复利的计算方式最符合实际的结论。
综上所述,经过多年的研究,间断现金流间断复利下一次支付、等额分付及等差、等比序列等值的计算研究已有丰硕的成果,其广泛应用于投资项目经济评价、按揭购房还贷、建设企业方案比选等工程经济问题中。另外,鉴于理论上计息时间的连续性,对连续复利的研究也相对成熟,其应用于垫资承包工程、股票投资等金融问题。但是对连续现金流连续复利等值计算的研究集中于公式推导和介绍,应用较少。
3 资金等值计算的基本参数
①利率或折现率i。折现率是根据未来的现金流量求现在现金流量时所使用的利率,一般对利率和折现率不加以区分,都用i表示。②计息期数n。利息计算中,计算期数即计算利息的次数。③现值P。现值即相对于将来值的任何较早时间的价值。④终值F。终值,也称将来值,是相对于现值的任何以后时间的价值。⑤年金或年值A。年金或年值是指特定时间段等额收支的金额,通常以等额序列表示,且发生在每期期末。⑥等差额(或梯度)G。等差額(或梯度)是当各期的支出或收入均匀递增或均匀递减时,相邻两期资金支出或收入的差额。
运用上述基本参数进行计算应用时需注意以下几点:第一,方案初始投资应假定发生在寿命期初。第二,方案实施过程中的经常性支出,假定发生在计息期(年)末。第三,P发生在0点,F发生在第n年年末。第四,A发生在每年年末,连续n次。若求解关系为P与A时,第一个A是在P发生一年后的年末发生;若求解关系为F和A时,最后一个A是和F同时发生。
4 资金等值计算公式总结
4.1 间歇现金流间断复利公式
对一次支付、等额分付类型等值计算公式的研究颇多,在此不再赘述与总结。
基于“一次支付、等额分付”六个基本公式,学者研究了等差、等比现金流序列间断复利计算公式,公式对比总结见表1。
4.2 间歇现金流连续复利公式
理论上,资金每分每秒都发生利息,因此,在实际中利息在一年中按无限多次计算,那么年有效利率为:
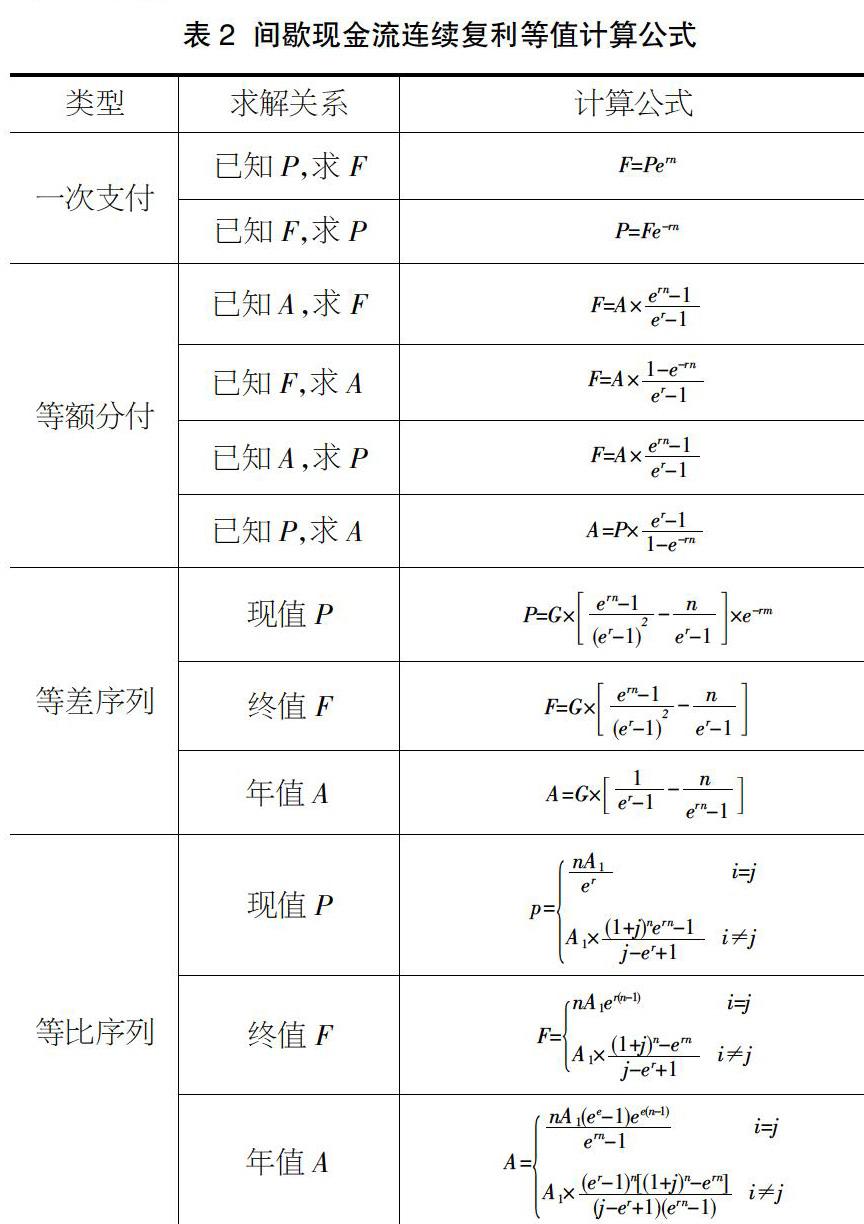
将利率i=er-1代入间断复利等值计算公式,得连续复利情况下各支付类型(一次支付、等额支付、等差系列、等比系列)的等值计算公式,具体见表2。
4.3 连续现金流连续复利公式
理论上讲,资金具有时间价值,资金在不停运动,但在工程经济问题分析中,往往简单认为现金流发生在年初或年末。因此,将连续现金流近似为间断现金流或是将连续复利近似为间断复利都是不够精确的,也是不符合实际的。连续现金流连续复利计算公式推导如下。
①现值计算公式。
5 结语
本文从间歇现金流间断复利、间歇现金流连续复利和连续现金流连续复利三个方面对资金等值计算的研究进展进行了综述,并总结了三种情况下各类型的计算公式。通过对当前研究侧重点的分析,提出最贴近实际情况的连续现金流连续复利的应用是今后研究的重点。
【参考文献】
【1】王恩茂.工程经济学[M].北京:科学出版社,2010.
【2】石璞.略论资金的时间价值及其等值计算[J].价值工程,1987(03):26-27.
【3】石璞.略论资金的时间价值及其等值计算(下)[J].价值工程,1987(04):21-23.
【4】韩卫涛.资金的时间价值及其等值计算[J].中国乡镇企业会计,1994(2):15-17.
【5】郭秀英,刘先涛,唐丽萍,等.论投资项目经济评价基础——资金等值计算[J].石油化工技术经济,2003(01):53-55.
【6】曾波.资金等值计算对传统按揭购房还贷方式的改进[J].商业时代,2007(20):92.
【7】沈浩.资金的时间价值及等值计算[J].山西建筑,2009,35(29):218-219.
【8】刘万鹏,田元福.间断复利与连续复利的比较研究[J].重庆交通大学学报(社科版),2009,9(4):59-60.
【9】杨卫军,鲍学英,赵延龙.连续复利资金时间价值在垫资承包工程中的应用[J].工程管理学报,2014,28(6):38-42.
【10】吴宏亮,莫俊文.连续复利连续现金流模型的建立及应用[J].兰州交通大学学报,2015,34(3):44-48.
【11】杨瑾.连续现金流连续复利的使用研究[J].淮陰工学院学报,2016,25(5):74-76.

