基于涡动相关法的沉积物-水界面氧通量与水动力条件响应关系

高学平，郭晓雪，孙博闻，张袁宁

（天津大学 水利工程仿真与安全国家重点实验室，天津 300072）

1 研究背景

沉积物-水界面（Sediment-Water Interface，SWI）作为水生态系统中的关键界面之一，是沉积物和水体之间物质垂向交换的主要场所，关于其物质通量的研究一直是国际上关注的热点问题［1］。溶解氧作为评价水体水质的常用指标，对于水生生物的生存、水体自净功能的维持等起着关键作用。SWI氧通量由于被广泛用于评估底栖生物的初级生产力、有机物矿化率，因此对研究水体物质循环、富营养化治理、生态系统功能等都具有重要意义。

目前关于SWI 氧通量的研究集中于分析通量与沉积物和水体中物质含量的关系。研究表明，沉积物有机物质含量、水体底部溶解氧浓度、泥沙粒径和叶绿素含量等因素均会对SWI 氧通量产生影响［2-4］。潘延鑫等［5］对农田排水沟的SWI 氧通量观测发现，上下游界面氧通量的差异可能与有机质、盐分含量及微生物活动等有关，但由于试验过程中水体处于静置状态，因此水动力条件同样可能是影响界面氧传输的重要因素［6-9］。Koopmans［10］和郑阳华等［11］通过原位和试验研究均发现SWI 氧通量随水平流速增大相应增大，Scalo 等［12］在构建氧通量代数模型中也将摩擦流速作为主要输入参数。从水动力条件对氧通量的影响机制来看，目前有学者提出水动力条件可能通过控制扩散边界层（DBL）厚度来实现对氧通量的影响［13-15］，DBL 作为控制沉积物-水界面物质垂向交换的主要瓶颈，与摩擦流速、雷诺数、Batchelor 尺度等水动力条件关系密切［9，16-18］，但结论多为定性描述。

对SWI 氧通量的测量一般可采用水底培养箱法、微电极剖面法和涡动相关法等。水底培养箱法通过分析封闭沉积物及其上覆水中溶解氧随时间的变化规律评估氧通量，该方法影响了观测区域与周围水体间水流交换，Brink 等［19］通过内部自带的水流动力装置模拟实际流动，依然难以还原真实水动力条件。微电极剖面法将微电极缓慢刺入沉积物内，根据溶解氧在沉积物-水界面的垂向分布得到氧通量，该方法虽然其垂直分辨率很高，但一般仅能获取垂向梯度的氧通量信息，难以反映地形变化、生物活动等对氧通量的影响；该方法的测量结果还存在偶然性，Røy［20］等发现三维的氧通量测量结果比一维条件下高约10%。针对上述测量技术的不足，Berg 等［21］首次将涡动相关法应用于SWI 氧通量测量，通过直接测量靠近沉积物表面处水体中流速与溶解氧值获得氧通量，可反映5 ～100 m2测量区域［22］（也称测量足迹）内的氧通量信息。这一方法由于对水动力条件影响小，因此在研究氧通量与水动力条件响应关系方面显示出独特优势。

本文基于涡动相关法理论基础，采用溶解氧传感器和声学多普勒点式流速仪构建了非侵入式涡动相关系统。通过室内试验对不同水平流速条件下溶解氧在沉积物-水界面的垂向分布进行观测，获得了扩散边界层厚度；根据垂向流速与溶解氧浓度的实时测量结果得到了SWI 氧通量，并详细介绍了氧通量求解过程及关键参数处理方法。将本文及相关研究中水动力条件、扩散边界层厚度及氧通量进行拟合，得到了SWI 氧通量与不同水动力条件间的定量响应关系，成果可以为SWI 氧通量对水动力条件的响应机理研究提供参考。

2 涡动相关法

2.1 理论基础涡动相关法最早可追溯到1950年代，起初该方法多用于分析物质、动量、热量等在陆-气、海-气边界层的交换。2003年Berg 等［21］首次将其应用于沉积物-水界面的氧通量测量，此后陆续有学者在水底边界层这一特定环境下对其理论进行改进，并开展了相关研究［15，23］。涡动相关法通过计算垂向流速与其它物理要素的协方差从而得到物质通量，基于质量守恒方程，溶质在控制体中满足：

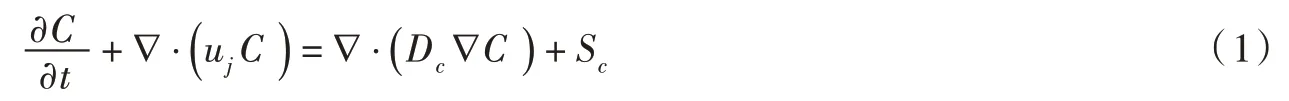
式中：C 为控制体内溶质浓度；uj=(u，v，w)为流速，j 为正交直角坐标系的三个方向；Dc为分子扩散系数，m2/s；Sc为控制体内溶质的源汇项；为控制体内溶质浓度的变化速率。

采用雷诺分解，将具有紊动特性的物理量分解为时均值和紊动值，即，代入式（1）得到：

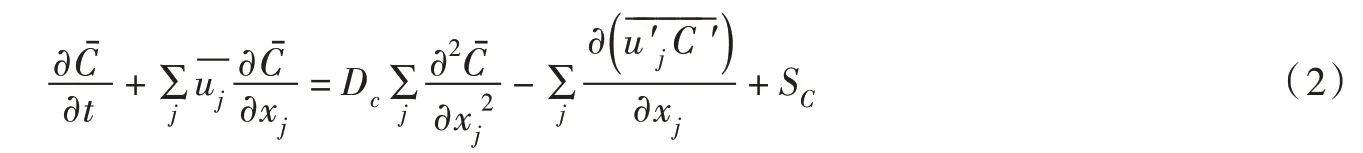
假设沉积物-水界面高度为z0，测点高度为zm，对式（3）两端同时进行积分可得：

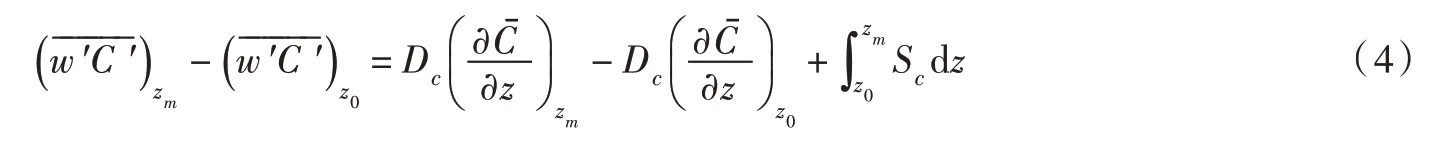
由沉积物-水界面的物质垂向传输方式（图1）可知，在扩散边界层（DBL）上部水体中物质的垂向传输机制主要为湍流扩散，而在扩散边界层内分子扩散起主导作用，因此测点距离沉积物-水界面很近，因此基于上述分析可得：

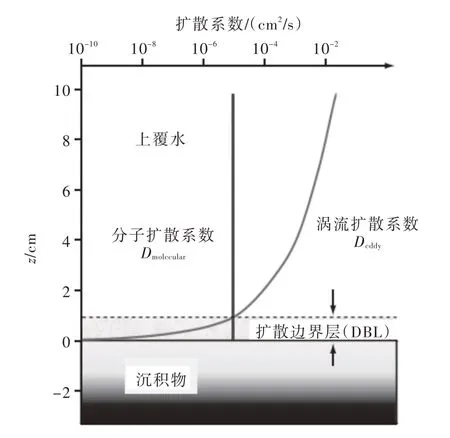
图1 沉积物-水界面物质垂向传输方式示意图［1］

式（5）说明沉积物-水界面处的物质通量可以用靠近沉积物处水体中某点的垂向流速与溶质浓度的协方差来表示。考虑到测量稳定性，通常需进行较长时段测量，因此沉积物-水界面物质通量：，其中n 为时段内数据个数。

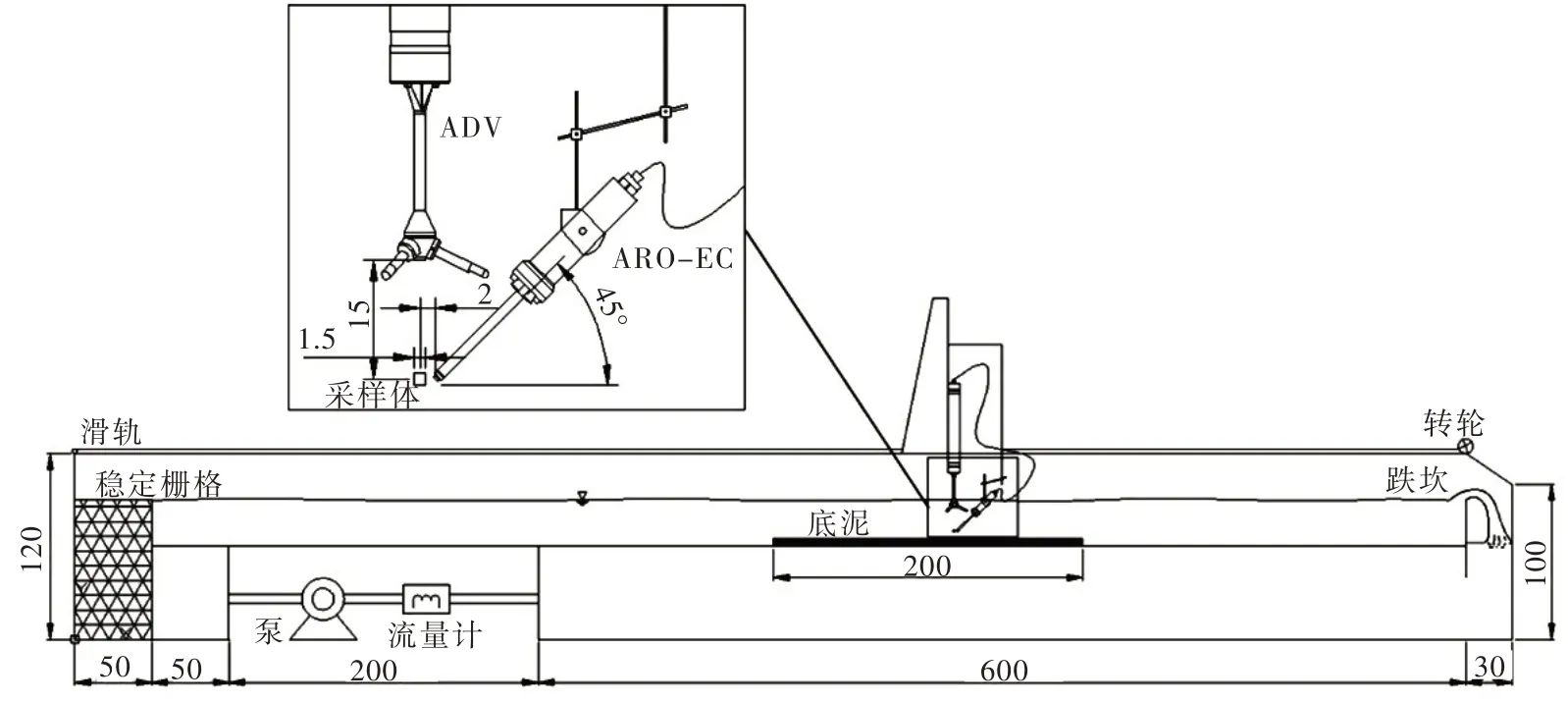
图2 试验装置及涡动相关系统示意图（单位：cm）

2.2 涡动相关系统构建本文采用的涡动相关系统（图2）由流速测量模块和溶解氧测量模块两部分构成。流速测量模块选用声学多普勒点式流速仪Vector6MHz（简称ADV），可以测量固定点的三维流速、流向、水压、水温、水深、波高等指标。ADV 内置电源和数据存储装置，提供两个模拟通道，采样频率为1 ～64 Hz，采样体位于信号发射端正下方15 cm 处，为直径15 mm，高度5 ～20 mm的近似圆柱水体；溶解氧测量模块选用快速响应的ARO-EC 型溶解氧传感器，可以测量固定点的溶解氧浓度及水温。ARO-EC 材质为钛，尖端直径12 mm，长164 mm，基于荧光寿命法进行溶解氧测量，在测量过程中不会引起信号漂移，可满足长时间观测需要。同时ARO-EC 为溶解氧温度双传感器，响应时间均小于0.5 s，可实现溶解氧的快速矫正，提高测量准确性。ADV 与ARO-EC 通过水密电缆连接，ADV 通过电缆控制ARO-EC 工作并为其供电，ARO-EC 可将测量数据通过电缆传输给ADV 并进行保存，两者协同工作，实现流速和溶解氧的同步测量。

3 材料与方法

3.1 试验装置试验装置如图2所示，该试验装置为长×宽×高=9.3 m×0.8 m×1.2 m 的长方体有机玻璃水槽，水槽采用自循环系统，分为上下两层，下层用于蓄水，上层为试验区域，中间用底板隔开，水体通过水泵在上下水箱中循环流动，试验过程中无外界水流流入流出。水槽上部铺设滑轨，并架设仪器固定支架，该支架用于固定涡动测量系统并可确保其在x、y、z 三个方向移动。

试验沉积物取自天津大学北洋园校区青年湖，为尽可能接近涡动相关法的适用环境，参照Donis等［24］的处理方法，试验前将底泥中的植物去除后均匀平铺于盛泥盒中，厚度约为5 cm，并用青年湖湖水进行7 天的静置培养。

3.2 试验设计整理涡动相关法应用的流速条件［14-15，21，24］，确定在0 ～10 cm/s 的流速范围对沉积物-水界面处的溶解氧垂向分布及氧通量进行测量。试验通过调节出水口处跌坎高度将水槽水深控制在30 cm；调节水泵阀门并读取流量计读数控制水槽入流流量进而计算得到相应试验流速，在0.65 cm/s、0.96 cm/s、3.09 cm/s、5.25 cm/s、8.35 cm/s 和9.69 cm/s 共6 组水平流速条件下分别进行如下测量：

（1）沉积物-水界面处溶解氧垂向分布测量：以5 min 为周期进行间歇采样，每个周期包括3 min采样时段和2 min 休眠时段，采样频率为64 Hz，采样模式由ADV 控制，在休眠时段通过调节支架高度控制溶解氧传感器的垂向位置。

（2）沉积物-水界面处氧通量测量：采用连续测量模式，每次测量时长为30 min，采样频率64 Hz，参考Chotikarn 等［25］在室内试验中涡动相关系统的布置方式，本试验测点位于沉积物上方5cm处，ARO-EC 探头位于ADV 采样体下游约2 cm 处，且与ADV 竖轴夹角为45°（图2），每组水平流速平行测量4 次。

4 结果与分析

4.1 溶解氧在沉积物-水界面的垂向分布试验选用的ARO-EC 型溶解氧传感器在垂向移动过程中可能会破坏沉积物结构，为减小仪器在沉积物中的移动距离，有效降低仪器对沉积物结构的破坏，因此采用与Jørgensen 等［26］类似做法测量溶解氧的垂向分布，进而分析不同水动力条件下DBL 厚度的变化规律。具体操作如下：

（1）确定DBL 下边界。从沉积物上方2 mm 处向下移动溶解氧传感器，通过多次平行测量获得溶解氧在沉积物-水界面较完整的垂向分布。图3为水平流速8.44 cm/s 下溶解氧的垂向分布情况，可以看出，不同高度处的溶解氧浓度的变化情况存在明显差异，在DBL 以上溶解氧沿垂向基本不变，当进入DBL 后溶解氧浓度随高度减小基本呈线性减小，根据溶解氧剖面中线性分布的“拐点”得到DBL的下边界，并记录相应高度。

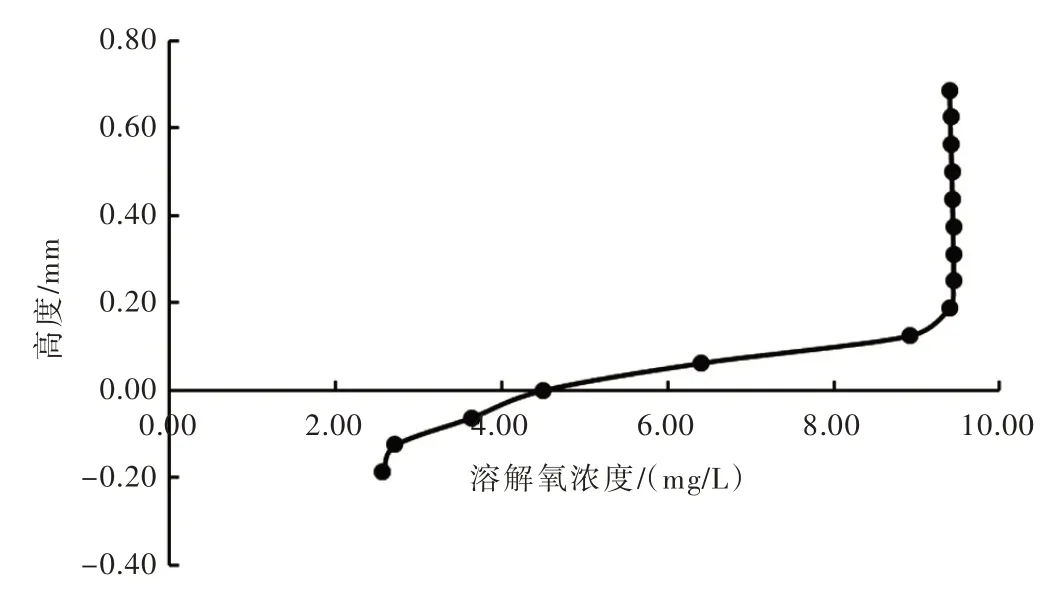
图3 SWI 溶解氧的垂向分布（水平流速8.44 cm/s）

（2）测量溶解氧垂向分布。以DBL 下边界为起始高度，向上移动溶解氧传感器，测量不同水平流速下溶解氧在沉积物-水附近的垂向分布。图4为溶解氧在沉积物-水界面附近不同水平流速下的垂向分布，可以看出，不同流速条件下沉积物-水界面处溶解氧的垂向分布存在明显差异。

图4 不同水平流速下沉积物-水界面处溶解氧的垂向分布及DBL 厚度

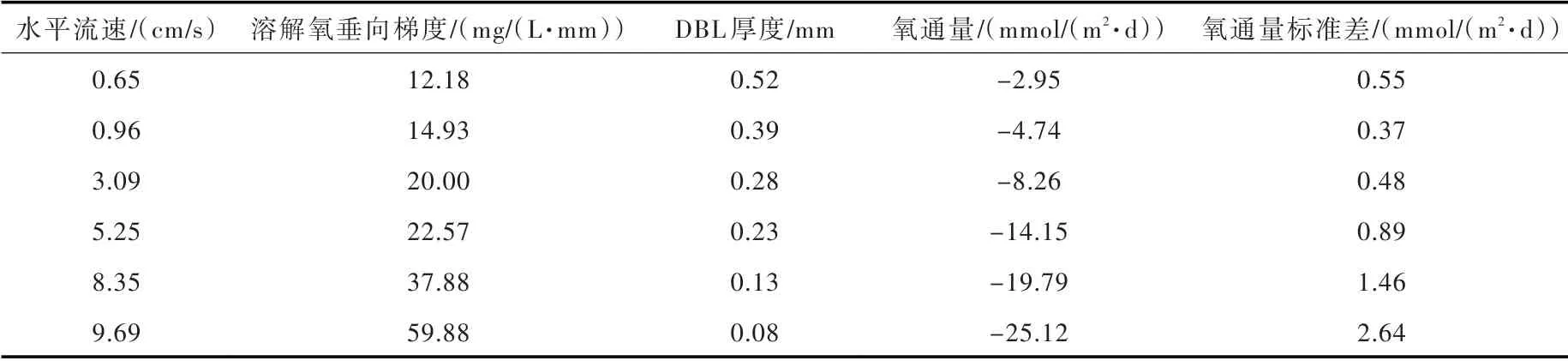
表1 不同水平流速下溶解氧垂向梯度、DBL 厚度和氧通量试验结果

（3）确定DBL 厚度。利用Jørgensen 等［26］提出的方法，将溶解氧线性浓度分布拟合线进行外延，外延线与溶解氧固定浓度的交点所对应的高度为DBL 厚度，相应结果列于表1。可以看出，水平流速为0.65 ～9.69 cm/s 时，相应的溶解氧垂向梯度为12.18 ～59.88 mg/（L·mm），DBL 厚度为0.52 ～0.08 mm，DBL 厚度随流速增大而减小。分析上述现象原因，随着水平流速增加，水体紊动程度增强，DBL 上边界处掺混随之加剧，这使上覆水与DBL 内溶解氧交换愈加充分，从而表现出DBL厚度相应减小。

图5 确定溶解氧和垂向流速滑动平均的窗口长度

4.2 溶解氧在沉积物-水界面的通量以15 min 为一时段进行氧通量计算，首先将64 Hz 的原始测量数据降噪（8 Hz），再进行去尖峰、坐标旋转校正、紊动值计算、时滞校正及通量计算，数据处理方法部分参照Kuwae 等［27］，下面就紊动值计算和时滞校正进行说明。

4.2.1 紊动值计算 湍流紊动值计算采用滑动平均法，该方法中滑动平均窗口长度的选取对氧通量的计算结果影响很大，当选取的窗口长度过小，会排除大尺度的紊动，造成通量低估；当选取的窗口长度过大，会引入非稳定成分，使得氧通量出现波动。为确定合适的窗口长度，将初始窗口长度设为1 s，计算该窗口长度下氧通量，之后逐渐增加窗口长度，重复进行上述步骤，获得不同窗口长度下的氧通量，当通量达到稳定时所对应的窗口长度即为合适的窗口长度，计算过程如图5所示。可以看出，当窗口长度为100 s 时，不同水平流速下的氧通量均可保持稳定，因此本次试验选取100 s 作为最终窗口长度。

4.2.2 时滞校正 ADV 与ARO-EC 空间位置分离及响应时间不同会造成溶解氧与垂向流速信号的不同步（时滞）。根据时滞产生原因，时滞的理论值应满足下式：

式中：x 为ARO-EC 尖端与ADV 采样体的水平间距，2 cm；U 为水平流速，cm/s；tr为ARO-EC 的响应时间，0.5 s。

由于氧通量结果对时滞取值较为敏感［28］，而理论时滞与实际情况存在一定偏差［24］，因此实际应用较少采用理论值。本文参照Lorrai 等［23］的方法确定实际时滞大小，首先参照相关研究中时滞大小［29］，确定时滞的取值为10 s，接着将溶解氧紊动值相对于垂向流速紊动值的时间序列进行移动，并计算两者的相关性，时滞即为最大相关性所对应的移动时间。利用Matlab 软件中的xcorr 函数进行时滞校正。图6为水平流速5.25 cm/s 下垂向流速与溶解氧紊动值相关性随移动时间的变化情况，可以看出，当移动时间为1.25 s 时，溶解氧和垂向流速紊动值的相关性最大，因此该水平流速下的时滞为1.25 s。采用相同方法，将不同水平流速下时滞的实测值与理论值进行分析（图7），可以看出，时滞随水平流速的增大而减小且与理论值拟合情况良好。说明理论时滞虽与实际情况存在一定偏差，但在实际应用中可以根据流速条件得到理论时滞值后，为时滞取值范围的确定提供参考。

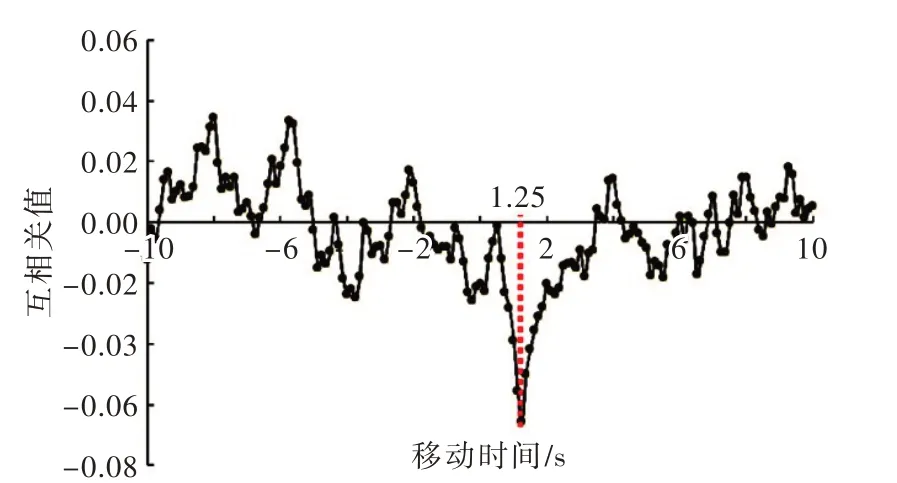
图6 垂向流速与溶解氧紊动值不同移动时间下的相关性（水平流速5.25 cm/s)）

图7 时滞实测值与理论值对比

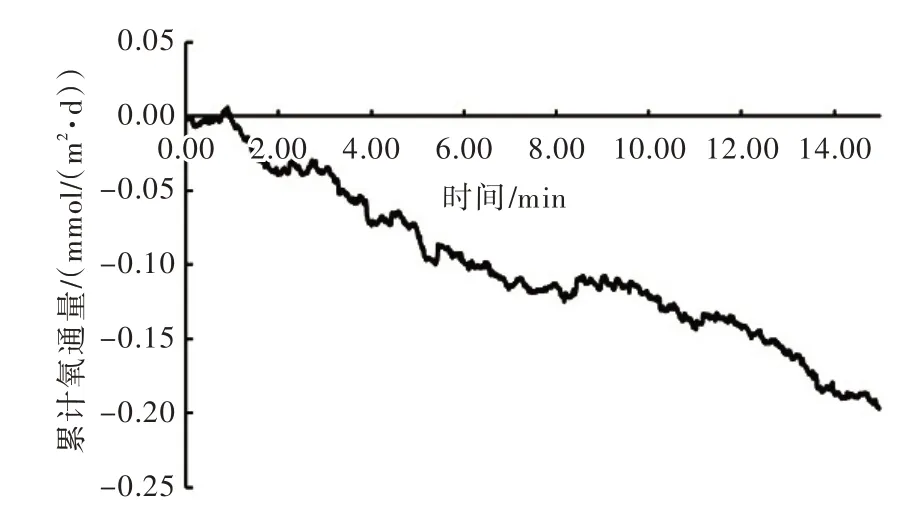
图8 累计氧通量

图9 氧通量在不同水平流速下的试验结果

为评估氧通量的数据质量，对15 min 内的氧通量进行累加得到累计氧通量（图8）。可以看出，累计氧通量有良好的线性趋势，说明试验过程的水动力条件稳定，通量数据质量良好。采用相同方法，得到不同水平流速下氧通量（图9，表1）。可以看出，水平流速为0.65 ～9.69 cm/s 时，氧通量为-2.95±0.55 ～-25.12±2.64 mmol/（m2·d），氧通量均为负值，说明测量点处的的沉积物以耗氧为主，并且氧通量随水平流速增加逐渐增大。

4.3 氧通量、DBL 厚度和水动力条件的关系由不同水平流速下溶解氧在沉积物-水界面附近的垂向分布可以看出，DBL 厚度随水平流速增大而减小，选取Batchelor 尺度对DBL 厚度进行参数化［30］，Batchelor 尺度表达式为：

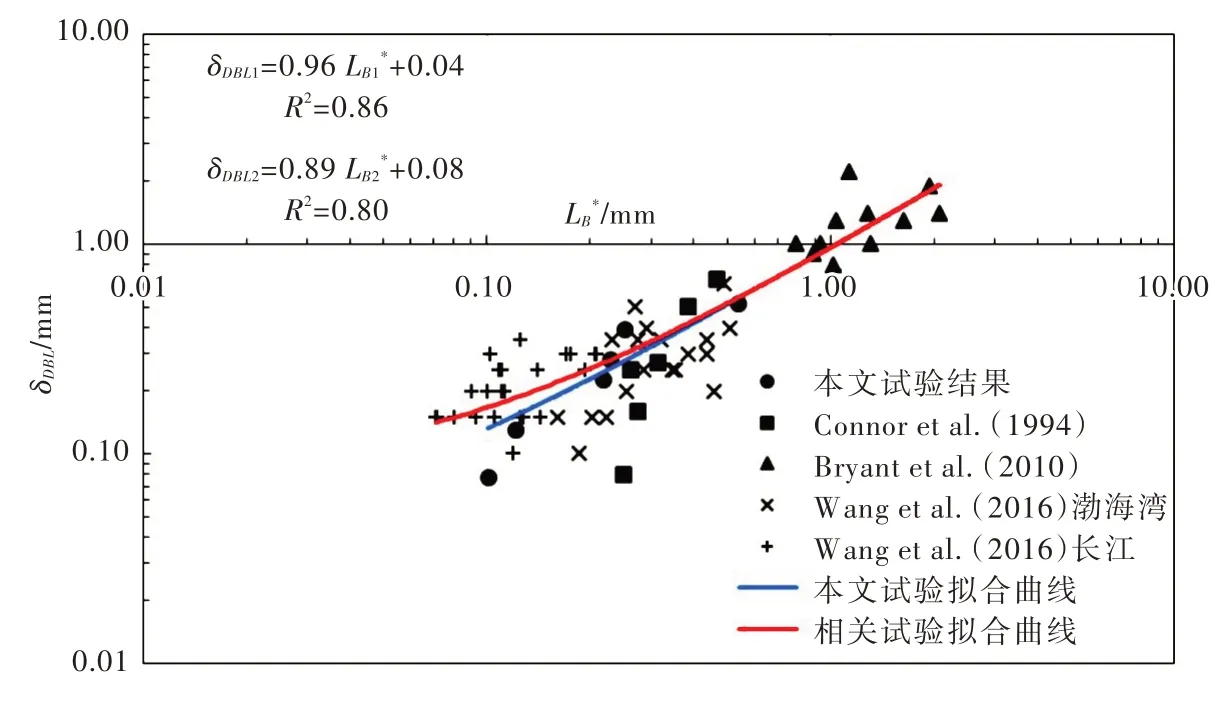
图10 DBL 厚度与Batchelor 尺度的关系

为分析水动力条件对DBL 厚度的影响，将DBL 厚度与Batchelor 尺度进行线性拟合（图10，蓝色拟合线），可以看出，DBL 厚度随Batchelor 尺度的增大线性增大，两者呈显著正相关关系，拟合关系式为δDBL1=0.96L*B1+0.04 ，相关系数为0.86。由于Batchelor 尺度可以表征湍扩散作用下标量波动所能保持的最小长度尺度，因此上述拟合关系式表明水动力条件对DBL 厚度影响显著。考虑到DBL 厚度较难直接测量，而计算Batchelor 尺度的相关参数较容易获取，因此对DBL 厚度进行参数化描述。整理相关试验结果［30-32］并根据式（7）得到Batchelor 尺度。将相关试验中DBL 厚度与Batchelor 尺度关系进行线性拟合（图10，红色拟合线），可以看出，本文和相关试验拟合曲线较为一致，拟合关系式为δDBL2=0.89L*B2+0.08 ，相关系数为0.80。考虑到相关研究中未对影响运动黏滞系数和分子扩散系数的水温条件进行实时观测，因此Batchelor 尺度计算值与实际情况可能存在偏差。但整体而言，本文与相关试验结果拟合公式中的参数非常接近，两拟合公式均说明Batch⁃elor 尺度与DBL 厚度基本呈正相关关系（相关系数约为0.9），因此在实际应用中可用Batchelor 尺度近似表示DBL 厚度。

为进一步研究DBL 厚度对氧通量的影响，将本文氧通量与DBL 厚度进行线性拟合（图11，蓝色拟合线）。可以看出，氧通量随DBL 厚度的减小线性增大，两者呈现负相关关系，拟合关系式为，相关系数为0.90，说明氧通量与DBL 厚度变化密切相关。整理相关研究［32-37］中氧通量与DBL 厚度并进行线性拟合（图11，红色拟合线），拟合关系式为相关系数为0.73。对比两拟合曲线，发现本文试验拟合曲线略高于相关试验拟合曲线，这可能是由于室内试验过程中排除了生物活动的影响所致。但整体而言，两条拟合曲线的变化趋势较为一致：当DBL 厚度小于0.5 mm 左右时，DBL 厚度变化对氧通量影响更强烈，氧通量随DBL 厚度减小迅速增大；DBL 大于0.5 mm 左右时，氧通量基本保持稳定。本文试验的DBL 厚度范围为0.08 ～0.52 mm，最大DBL 厚度对应的水平流速为0.65 cm/s，结合Glud 等［13］的试验结果，可以说明DBL 厚度大于0.5 mm左右时，氧通量基本保持不变。

图11 氧通量与DBL 厚度的关系

4.4 讨论通过将本文与相关研究结果对比，可以发现尽管不同研究中的沉积物的有机质含量、孔隙度等条件存在差异，但水动力条件、扩散边界层厚度、氧通量三者间的变化规律接近，即水动力条件对DBL 厚度影响显著，Batchelor 尺度与DBL 厚度基本一致；DBL 厚度在小于0.5mm 时对氧通量影响剧烈，大于0.5 mm 时，氧通量基本保持稳定。分析其原因一方面可能是由于物质通过分子扩散、弥散及湍流扩散三种作用在SWI 进行传输，而在沉积物渗透雷诺数较高的环境下，最易受水动力条件影响的湍流扩散会成为物质在SWI 垂向交换的主导方式［38］。另外，在其它因素较为稳定的情况下，水动力条件会引发扩散边界层厚度的改变，而SWI 物质的垂向交换必须经由扩散边界层，使得其厚度变化较总氮、总磷、叶绿素含量等对SWI 氧通量的影响更为直接。因此表现出水动力条件会在某种程度上“掩盖”其余因素对氧通量的影响，对于这一现象Murniati 等［7］也有类似阐述。考虑到多年来人们对于SWI 的物质通量交换大多采用Ber⁃ner 等［39］于1980年建立的反应-输运模型（Reaction-Transport Model，RTM）进行描述。在这一模型中扩散层厚度是关键影响参数，因此本文得出的水动力条件可以通过改变扩散边界层厚度进而影响氧通量的定量规律，也可适用于氨氮、硝酸盐、可溶性有机碳等其它溶质在SWI 的交换规律研究。

本文对DBL 厚度进行参数化时依据相关研究中湍流耗散率的参考高度进行Batchelor 尺度的计算，关于Batchelor 尺度与DBL 厚度的内在联系尚待深入研究。此外，尽管不同环境条件下氧通量与DBL 厚度的变化趋势一致，但是DBL 厚度对应的氧通量存在差异，这可能与水体及沉积物性质有关，后期可加强氧通量与孔隙度、渗透性、有机质含量、营养盐浓度等静态因素间响应关系的研究。

5 结论

本文围绕沉积物氧通量与水动力条件间响应关系问题，较为系统地阐述了涡动相关法的原理及实现方法，基于此开展了不同水动力条件下扩散边界层厚度及氧通量变化的试验研究，主要结论如下：

（1）随着水平流速的增加，扩散边界层厚度逐渐减小，氧通量逐渐增大。水平流速为0.65 ～9.69 cm/s时，扩散边界层厚度为0.52 ～0.08 mm，氧通量为-2.95±0.55 ～-25.12±2.64 mmol/（m2·d）。

（2）水动力条件对扩散边界层厚度的影响明显，扩散边界层厚度与Batchelor 尺度呈正相关关系。考虑到扩散边界层厚度较难直接测量，而计算Batchelor 尺度的相关参数较容易获取，因此实际应用中可采用Batchelor 尺度近似表示扩散边界层厚度。

（3）当扩散边界层厚度小于0.5 mm 左右时，扩散边界层厚度变化对氧通量影响更强烈，氧通量随扩散边界层厚度减小迅速增大；当扩散边界层厚度大于0.5 mm 左右时，氧通量基本保持稳定。