Discrimination geochemical interaction effects on mineralization at the polymetallic Glojeh deposit, NW Iran by interative backward quadratic modeling
·
Abstract The physico-chemical exchanges between hydrothermal fluids and the host rock are usually controlled by elemental interaction effects. A criterion-based backward elimination approach applies the iterative regression analysis and analysis of variance to investigate the geochemical features of the polymetallic Glojeh (Au–Ag–Cu–Pb–Zn) deposit in NW Iran. A statistical definition of the elemental interaction effects (Xi-j2 , Xi × Xj) could elucidate the relationship between variables and the performance of a full quadratic polynomial model (QPM). The model optimization procedure was carried out by the removal of insignificant predictors(P value 95%CL)based on R2(pred.)criterion.In order to straighten the convergent trend with R2 and R2(adj.), R2(pred.) gradually increased from 0% to 77.8% by 15-steps optimization. The miniature-scale geochemical changes indicate double ordinal Au(Ag, Pb) and Au (Ag, Zn) interactions within the vein and host rock, in QPM. Results show that the Au (Pb–Zn)commonly presents ordinal effect at the vein and disordinal interaction at the host rock. This ordinal–disordinal interaction revealed that elements Pb and Zn have similar geochemical features during mineralization. In addition,Akima’s polynomial contour map confirms the results from Pb–Zn interaction effects by dependency tracing between Au–Pb–Zn at different populations. However, it is noteworthy that Pb and Zn occur together in the second phase of Pb–Zn–Cu ± (Ag ± Cd) sulfide mineralization at Glojeh,which implies intergrowth and interaction of Pb–Zn on Au concentration. Pb and Zn demonstrate relatively high mobility and are generally concentrated in the near surface zones. Nb is an immobile element during alteration and high content Hg zone is mainly restricted to narrow stripes above ore vein and veinlets.
Keywords Backward Elimination · Quadratic polynomial model · Miniature-scale changes · Ordinal–disordinal interaction effect · Akima’s polynomial contour map ·Immobile element
1 Introduction
Physico-chemical properties of fluids and host rocks are the main factors controlling the hydrothermal fluid migration(Hagemann and Lu¨ders 2003; Li et al. 2017; Mao et al.2011; Xiao et al. 2018). The interaction between host rock and vein bodies causes different dispersion pattern of elements (Darabi-Golestan et al. 2015; Xiao et al. 2017;Heinrich 2007; Steefel and Maher 2009). When there are elemental interaction parameters within a dataset, the relationship between geochemical variables and target elements could be examined (Doove et al. 2014). The interaction processes are very complicated and usually varied with hydrothermal fluid temperature, pressure and alteration grade of host rock (Bendezu´ and Fontbote´ 2009;Kelley et al.2006;Steefel and Maher 2009).An interaction may be ordinal or disordinal with respect to multiple variables (Darabi-Golestan and Hezarkhani 2016). There are two main hydrothermal ore veins and several veinlets(epithermal brecciated zone) in the Glojeh polymetallic(Au, Ag, Cu, Pb, and Zn)deposit, which show remarkably variation with host rocks, in composition, structure,texture, and genesis (Darabi-Golestan and Hezarkhani 2016; Mehrabi et al. 2014).
Due to the distinct and miniature changes in elemental concentration between the veins and host rocks, an evaluation of geochemical data should be conducted prior to any interpretation (Gustavsson et al. 2012; Lima 2008; Xiao et al. 2012). Sampling and laboratory analysis are the two main factors to affect data precision (reproducibility) and quantify of the amount of variations in the dataset (Matysek and Sinclair 1983). Stepwise regression analysis (RA)and analysis of variance(ANOVA)are mainly based on the forward selection (by adding), Backward Elimination Approach (BEA; by deleting), and stepwise methods (simultaneously adding and deleting the predictors) to evaluate a small subset of the predictors within the regression models (Chun et al. 2016; Cordell and Clayton 2002;Granian et al. 2015; Pasandideh et al. 2014), which have been widely applied to discriminate indicator elements association in some ore deposits(Xiao et al.2012;Yousefi et al. 2014; Zuo et al. 2013). The BEA is commonly less adversely affected by correlations of predictors among these methods(Azadi and Almasganj 2009;Figueiredo and Jain 2002; Myers et al. 2016). The backward stepwise algorithm based on different criterions [R2, R2(adj.), R2-(pred.), the PRESS, F- and student’s T-functions] on a certain confidence level (CL) has been applied by many researchers in various surveys (Borah et al. 2015; Briand and Hill 2013; Garson 2012; Myers et al. 2016). The convergent trend of R2, R2(adj.) and R2(pred.) accompanied by increasing F value, and decreasing Predicted Residual Sum of Squares (PRESS) are the indications of a more accurately optimizing process (Barbin et al. 2016;Mousavi and Parvini 2016). This method is helpful to assess the temporal stability and the interaction between elements dispersion pattern, and indicator element associations during mineralization(Garson 2012;Li et al.2010).The first order(X),second order(X2),and interaction terms(Xi× Xj) can be distinguished as predominant predictors in the model due to the different elemental mobility.These interactions have been used to detect small scale variation and spatial heterogeneity in environmental sciences(Gupta et al. 2015). Therefore, detecting the characteristic of elements could exhibit significant changes in mobility on the vein and background environment by applying those methods (Yousefi et al. 2014). Understanding the interaction terms derived from the veins and contact host rocks are very important for the comprehension of mineralized processes (Ettler et al. 2003). We use Akima’s interpolation function to obtain a spatial linear interpolation between those data (Hoang and Nguyen 2016).
The main objective of this study is to optimize the Quadratic Polynomial Model (QPM) to have a better prediction for new observations. Discussions mainly include f test and t test criteria, and the graphical comparison is made on R2, R2(adj.), R2(pred.), and PREES variation.Based on optimized QPM, the interaction between elements was investigated to indicate the spatial heterogeneity and element mobilities between ore veins and host rocks.Besides, the different interaction effects between elements were also discussed by using the optimized model, which were shown as the Akima’s polynomial contour maps.Darabi-Golestan and Hezarkhani (2016) discussed these methods based on F values, while the interaction effects were restricted to the first order.Three main questions need to be further discussed:
1. Due to the different order of mineralization and variability, interaction terms (Xi× Xj), and squared terms(X2)of variables were used among the first order of elements. What are the main significant character and term of variables?
2. A technique might be used to create an appropriate model.
3. What are the statistical properties (e.g., confidence interval) and variability of elements between different environments by application of the interaction parameters (which discussed by Doove et al. (2014) as a standard approach to implement multiple relations)?
2 Geological setting
The polymetallic Glojeh deposit is located at the north Zanjan City,NW Iran.This deposit occurred in the Tarom–Hashtjin Metallogenic Province(Fig. 1)which is one of the main metallogenic provinces in Iran(Mehrabi et al.2014).The other main zones are Orumieh–Dokhtar belt and Sanandaj–Sirjan belt. The Glojeh polymetallic deposit shows an intermediate-high grade ore (Gold content varies from 1 to 15 ppm)in the vein, veinlet and brecciated zone with a length of greater than 1.5 km and a width ranges from 0.1 to greater than 4 m (Mehrabi et al. 2014). Previous studies and our field observations indicate that the deposit is most probably classified as intermediate-high sulfide epithermal ore deposit.
The most abundant rock types in the Glojeh polymetallic deposit are rhyodacite (major host rock), rhyolite, tuff,andesite, andesitic basalt, trachy-basalt, and trachy-andesite(Bahajroy and Taki 2014;Ghorbani 2013).Regional magmatism generally occurred from Late Cretaceous to Quaternary, and the main forming period is Eocene.Intrusive rocks at the area are mainly granodiorite, granite and quartz-monzonite (Mehrabi et al. 2014), which belong to metaluminous and shoshonitic range and generally intrude into the volcanic and sedimentary rocks.

Fig. 1 Simplified tectonic map of Iran(a),geological map of Tarom–Hashtjin Metallogenic Province (b),and Location and geological map of the Glojeh deposit,including main trenches and boreholes(c).BH2N1 is a main borehole that have the same azimuth of 180°are shown in AA′cross section. After Darabi-Golestan and Hezarkhani (2016)
Mineralization of the study deposit can be subdivided into three stages. At the first stage, showing vuggy and massive silica bodies (vein and veinlets) and mainly formed magnetite, quartz, and Cu sulfide minerals which are possibly associated with magmatic-hydrothermal fluid boiling in a high P–T condition.The second stage is related to the mixing of hydrothermal fluids and meteoric waters,which demonstrated as deposition of As–Sb–Fe–Cu–S and Pb–Zn–Cu–Ag assemblages of galena, sphalerite, chalcopyrite, and sulfosalts. Finally, the third stage is the dominated sources of Au and Ag (Bi–Pb) as A and B mineralized veins at Glojeh (Fig. 1c) as low-sulfide mineralization, which is characterized by a variety of precious and sulfosalt minerals, hematite and goethite from supergene alteration.
The two main polymetallic A and B Au–Ag–Cu–Pb–Zn mineralized veins and veinlets with east–west striking at the Glojeh mineralization occur within rhyodacite host rock. The alteration mainly includes silicification, sericitization, argillization and propylitization which varies from mineralized veins to host rocks. Ore minerals mainly consist of pyrite, chalcocite, chalcopyrite, covellite, enargite, bornite, famatinite, sphalerite, galena, tennantite, and Ag-bearing minerals. Magnetite and hematite, Bi-bearing minerals with electrum, and native Au are also found in previous works (Siani et al. 2015). These ore minerals generally present massive, disseminated, replacement,open space filling, and stockwork veins.
3 Sampling and chemical analysis
Data mainly originates from 679 samples which collected from 11 drilling boreholes with a total of 1503.24-m length. The boreholes named as BH1N1, BH1N2, BH1-2N1, BH1-2N2, BH2N1, BH2N2, BH2-3N1, BH3N1,BH3-4N1, BH4-5N1 and BH5N1 (Fig. 1c). All boreholes were drilled with a dip of 45° and azimuth direction of 180° (same as trenches) in the area (Fig. 1c). Exploration trenches consist of seven trenches named as TR0 to TR6(total of 932-m excavation presented by 387 samples) in the first phase (Fig. 2). Furthermore, during the second phase, five trenches of TR1-2 to TR5-6 (total of 482.8-m excavation presented by 487 samples)have been excavated among the previous trenches (Figs. 1c, 2a). An AA′cross section map along the BH2N1 and TR2 is depicted at the middle right of Fig. 1, which both A and B cross cutting veins are shown. A and B major polymetallic veins are intersected by BH2N1 at the depth of 26.2–33.9 m and 79.68–81.51 m, respectively (Fig. 1c). The total depth is about 140 m, and 127.69 m is discovered with rhyolitictuff rocks and 12.31 meters hosted in the brecciated veins.These two main polymetallic Au–Ag–Cu–Pb–Zn veins and several veinlets follow an east–west striking. Quartz is the main gangue mineral at the Glojeh area (Fig. 3).
Rock chip-channel sampling of trenches and boreholes were done, according to instructions. The composite sampling procedure applied to decrease the cost of analyzes(Correll 2001). The sampling interval at ore veins and shear zones were 1 m. The appropriate samplings interval at the adjacent host rocks and outer host rock were 1.5 and 5 m, respectively. A total of 874 and 679 composite samples were taken for analyzing from 1414.8 m and 1503.24 m of trenches and boreholes,respectively(Darabi-Golestan and Hezarkhani 2018d).A total of 153 samples of BH2N1 were analyzed by inductively coupled plasma mass spectrometry (ICP-MS) for 44 elements at Earth Sciences Development Company Lab of Iran. Only a few elements in analytical data represent values below the detection limit(DL). Ag, Co, Cr, Hg, Nb, Ni, Sc, Se, Tl, and U elements represents censored values, where the detection limit values are 0.1, 0.2, 1, 0.05, 1, 0.5, 0.5, 0.05, 0.6, and 1 ppm.Accordingly,the total numbers of censored values were 62,28, 4, 72, 5, 27, 4, 6, 17, and 42 for each element,respectively. The below D.L. data were replaced by half the detection limit value. All the other lithogeochemical samples were analyzed for polymetallic (Au, Ag, Cu, Pb and Zn)elements.Au was analyzed by fire assay technique in Zarkavan lab, Ag, Cu, Pb and Zn were detected by Atomic Absorption Spectrophotometry (AAS) at Earth Sciences development company lab of Iran.
4 Methodology
4.1 Interaction effect
Rather than the application of the first and second interactions at the ANOVA model, the Akima algorithm has been used to demonstrate geochemical interactions and elemental dependency in exploration. The Akima interpolation method could reveal the X, Y, and Z values at a particular point using a third order piecewise polynomial function. Accordingly it will facilitate complex elemental interactions by a contour map model which represent three elemental changes (Fried and Zietz 1973; Inomata et al.2016). It is based on a piecewise function composed of a set of polynomials, and applicable to successive intervals of the given points (Akima 1970). The x- and y-values include the related mesh, and z-value to be used at the boundaries (Naprstek and Smith 2016). All the Akima’s polynomial contour map of three variables at this study were depicted in MINITAB Inc. version 16. By default,Minitab software uses the minimum z-value at each point.Each piece-wise polynomial point is determined from the six points around (three on either side) (Patki et al. 2015).

Fig. 2 Several field photos from the polymetallic Glojeh deposit.Exploratory trenches and veins the positions(view to the west)(a).Vein and veinlet zone between TR2 and TR3 (b). Vein, veinlet and silicic zone between TR3 and TR4 (c)

Fig. 3 Quartz occurs as comb texture in the low sulfidation stage(the third stage) and resulted from dilution by meteoric water
4.2 T test and F test criteria
P values were determined using calculated t values and the df for probability function, according to the TDIST function(TDIST(t value,df,2 tails) = P value),where t value must be non-negative (Darabi-Golestan and Hezarkhani 2018c;Remenyi et al.2011).The TINV[TINV(P value,df) = t value]controller function calculates the inverse of the two-tailed student’s t-distribution (Sze´kely and Rizzo 2013). The df is the degreesoffreedom.TtestfollowsStudentt-distributionanditis applied when the standard deviation is not known and the sample size is small(Larose 2006).Therefore,the P value is used to determine whether the factor is significant(Fig. 4).
F test follows f-distribution, where it can determine the equality of the variances of the two normal populations(DeCoursey 2003; Hill et al. 2006). In addition, using this function it will be able to compare two population variances (Fig. 4). The value of the FDIST function was used to test the significance of linearity performance.P value or α is defined by inverse cumulative distribution function of Fisher’s F-distribution(Borah et al.2015).The F test must be compared against a critical F value that can be calculated or found in reference tables. If it is lower than 0.05,then a relationship between independent and dependent element is approved and as long as this difference is lower than 0.05 (FDIST <<0.05), the result shows that it has been achieved by no chance (DeCoursey 2003).

Fig. 4 The differences between the t test and F test in order to determine whether a factor or a populations is significant
4.3 Multiple regression analysis
Multiple regression analysis and analyses of variance(ANOVA)are the useful statistical techniques for modeling a variable which is influenced by several parameters(Montgomery 2017).If the model provides an estimation of the true response via independent variables, it is important to examine the fitted model with an adequate approximation. In the present study, some criteria such as R2,R2(adj.), R2(pred), PRESS and F value were applied to analyze the model adequacy. The regression analysis and the ANOVA were conducted in Minitab Statistical Software (version 16.0). The F-ratio, sum of squares due to regression (SSR) and the residual sum of squares (SSE which is called the decomposition of the total variation)are calculated from ANOVA (Borah et al. 2015; Briand and Hill 2013; Garson 2012) analysis as seen in Table 1.
The total sum of squares (SST) is given as SST =SSR +SSE (Hasanien et al. 2010; Menard 2000).Accordingly,mean squares of regression (MSR) and mean squares of error (MSE) is determined and the F-ratio is calculated from Eq. (1):

whereas, R2is obtained by SSR/SST. When R2is closer to 1, the regression equation could estimate better responses which fit on the real data.Regarding the fact that a variable is important or not,adding the variable to the model always accompanied by increases of R2. To overcome this problem, R2(adj) is used while it will not necessarily increase by adding a variable(s) to the model. Actually, adding an unnecessary variable to the model leads to a decrease of R2(adj.). Whereas, R2(pred.) was used to compare how well the model predicts responses for new observations that were not included in model estimation based on leave-oneout cross validation (Ali et al. 2014; Coruh and Elevli 2014).The PRESS criterion value was used to calculate the predictive ability of the model’s related to the R2(pred.).The model with the lowest PRESS value may be the desirable stage of the process, if the prediction is the objective of the method (Wang et al. 2016). Hence, the predictive sufficiency of the model is evaluated by R2-(pred.), and F-ratio (Darabi-Golestan and Hezarkhani 2016).The full quadratic polynomial model(FQPM)which is constructed in the first stage is restricted to second-order interactions. It is given by Eq. (2):
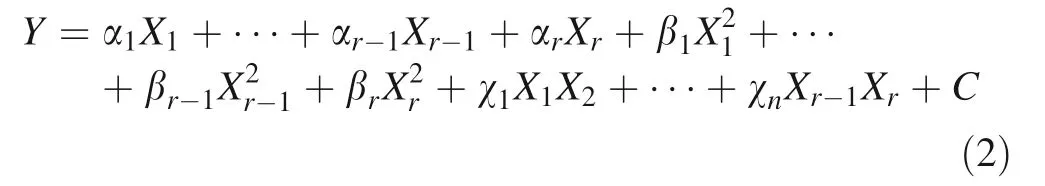
where α, β and χ are the coefficients, and Xris variables.Based on different R2and R2(pred.), F-ratio, and P values criteria the model could be optimized by BEA.
4.4 Backward elimination
The objective of this method is to optimize the responses due to the mentioned criteria. Therefore, this efficient method cause to reduce order or predictors in the model(Yadav et al. 2013). Accordingly, the level of significance is considered at 5%for each variable,that is,α = 0.05.The Full QPM includes all variables,while the majority of them have high P values (α). Therefore, to build an optimized QPM, all these insignificant variables should be omitted,step-by-step (Samal et al. 2008). Across this approach, R2,R2(adj.), and R2(pred.) show a convergence trend until the model is optimized(Zhao et al.2014).The increasing trend of R2(pred.)and F value are to continue by removing each insignificant predictors(Puri and Banerjee 2013).The BEA is implemented through model initialization (or model learning), order reduction, and denoting the model validation (Azadi and Almasganj 2009).

Table 1 The results of ANOVA analysis
5 Results
5.1 Interaction effect
Twelve elements (Ag, As, Cu, Hg, Mn, Nb, P, Pb, Sn, Sr,U, and Zn) are identified as significant factors, the first order interactions (covariates Xi× Xj; such as Ag × As,Ag × Cu … U × Zn) effects and quadratic terms (covariates Xi2, Ag2, As2, …, Zn2) can be applied for better modeling.The Au is the response variable,and the analysis can start as a function of all the 12 elements and full interaction effects. It can be expressed as follows:

The variables xiand xjare compositional data where the response of modeling for Au depends on them, while the threshold value is denoted as C.
5.2 Backward elimination by multiple regression analysis
Totally, there are 137 degrees of freedom (df) in the 1st stage of modeling, with 90 degrees of freedom for regression and 47 df for residual error.The df for regression at each stage indicates a number of predictors and the df for residual error calculated from(samples—predictors).If the threshold value (C) to be considered, the dfdf of residual error was calculated from n - p - 1(n = 138,p = 90 and C = 1) which was equal to 47 (Table 2). The high R2(equal 92.10%) and small R2(pred.) equal 0.0% suggested that the model is not an optimized model and there is not a good sufficiency for predicting new observations at the first step. Therefore, the BEA was carried out by omitting the least useful predictors and interactions according to partial F-ratio, R2, R2(adj.), and R2(pred.) criteria. The results of regression analysis and ANOVA are summarized at Table 2 for different steps, and insignificant predictors are determined by highest P values.The insignificant Ag × P,Ag × Zn, Pb × U, U2, and Ag × Nb interactions which have the largest P values (respectively equal to 0.928,0.903,0.882,0.853,and 0.786)are removed at the 1st step.By eliminating these five insignificant interactions at the second step,the df of the regression is decreased to 85 and df of the residual error would increase to 52, compared to the first step. The R2(adj.) increased slightly, while not sensitive changes in R2(pred.) indicates that some of the predictors (As × Hg, Cu × U, As × Sn, Mn × Pb, and As × P) still have high error rate (P value or α) in the second model. Hence, they were eliminated in the third step and R2(pred.) increased from 0.0% to 19.91%. The R2(pred.) is related to PRESS value that gradually decreases across 13 steps,from 191.246 to 29.860(Fig. 5).By eliminating Pb2and Nb × Pb (with the P value of 0.06), there is an obvious change in the variation trend of R2(pred.) and PRESS value (Table 2). Hence, it is better that these predictors survive in the model and after step 13,just threshold value is eliminated (step 15) from the modeling which verified by decreases of PRESS value from 29.860 to 29.148. Accordingly, in the last step the regression, residual error and total df are equal to 36, 102 and 138, respectively (Table 2; stage 15).
After 15 steps of optimization and removing insignificant predictors,R2(pred.)increased from 0.0%at the first step to morethan77.80%atthe optimizedmodel(Table 2;Fig. 5).In this process of optimization,the R2and R2(adj.)show slightly decreases from 92.10%to 89%and increases from 77.10%to 85.2%,respectively.Meanwhile,R2(pred.)variation is more important to examine the predictability of these models,and it was achieved after 15 optimization steps(Table 2 and Fig. 5).Finally, R2, R2(adj.), R2(pred.) show a convergence trend during 15 steps.This means that the applied strategies can be adopted in order to reach an optimized model.
The minimum P value at the 13th step is approximately 0.06 (for Pb2and Nb × Pb), which is nearly approved by significant level α = 0.05. Besides, by eliminating these predictors R2(pred.) is decreased and the PRESS is increased. Therefore, these predictors cannot omit and a significant level of α = 0.06 is considered at the optimized model. Totally, 36 (df of the regression at step 15) significant predictors remained after eliminating 54 insignificant predictors from 90 (df of the regression at first step) initial predictors (Eq. 4, Fig. 6). Accordingly, the final estimated regression model using the BEA of the variables is expressed as follows:

The Sn, U, Pb and P × Sn, As × Zn, Hg × P, and Ag × Sn predictors have been considered as the mainsignificant predictors and significant interactions of the optimized model, respectively. It was calculated based on related t values that determined by dividing the coefficient on the standard error of coefficients. The t test was also used to find out whether each of the regression coefficients is significant (Granian et al. 2015), it was done by considering the P values. All the stages of the discussed approach are presented in Fig. 6, which indicated the difference between the t test and the F test for easier understanding. All the 90 predictors at the 1st stage of optimization included within the first box. Each box contains first and second order and interaction terms of Ag,As,Cu,Hg,Mn,Nb,P,Pb,Sn,Sr,U,and Zn.At each stage,all the t values were calculated for elements which contributed in the model at the different stages (Fig. 6). On the other hand,F test,R2,and R2(pred.)are the objectives criteria to
examine the predictivity of the proposed model at each step(Fig. 6).The first five predictors that have the least value of t test must be eliminated at each step (they were depicted by red line within each box). The second stage of optimization was defined by 85 predictors. At each step, a separate t test was conducted for all the predictors that participate in modeling. On the other hand, the F test considers the linear relationship between Au and set of predictors which participate in a different stage of the interactional model. Subsequently, the process was repeated until 36 main significant predictors remained.
Elimination of Pb2and Nb × Pb lead to decrease R2(pred.)and an increase of PRESS, which not in order of optimization.

Table 2 Staged BEA for analysis of variance (ANOVA)based on statistical parameters and the P value of each predictor

Fig. 5 Graphical comparison of R2,R2(adj.),R2(pred.)variation in order to improve the numerical model while PRESS value confirm this trend in 15 steps
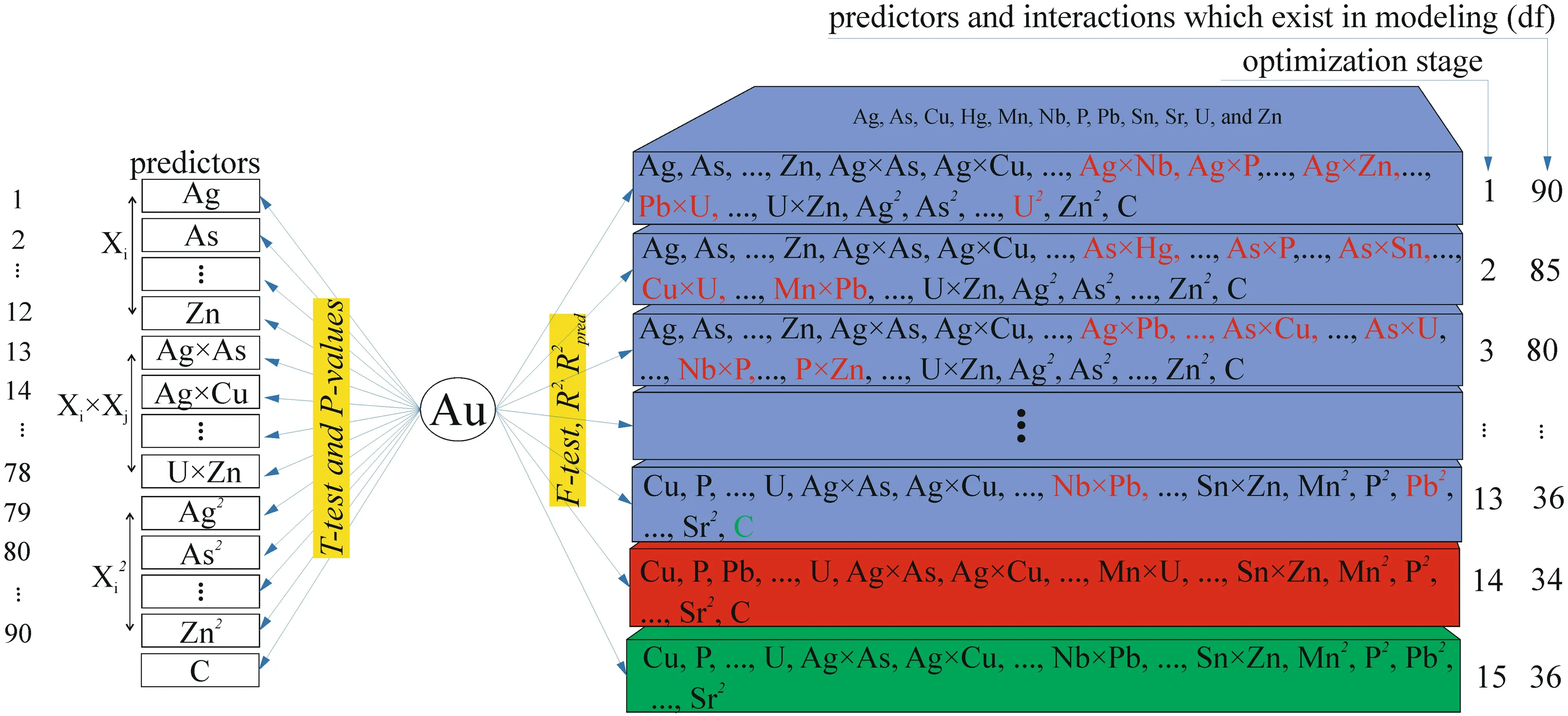
Fig. 6 The differences between the t test and F test and the order of elimination for optimizing the process-based interactional model

Table 3 The statistical summary of the trace-elements that presented in the optimized model in orebodies and wall-rocks
In order to exhibit the characteristics of geochemical data, the statistical summary of the trace-elements is presented in Table 3. The element contents and statistical information(mean,sum,standard deviation,minimum,the first quantile, median, the third quantile and the maximum values)categorized in orebody(veins or veinlets)and wallrock (Background) data sets. The mineralized and background samples were identified by Darabi-Golestan and Hezarkhani (2018b) and Darabi-Golestan and Hezarkhani(2018a). Accordingly, the background and anomalous population were determined for BH2N1 borehole by 126 and 12 samples,respectively(Table 3).The mean values of Au, Ag, As, Hg, Mn, Nb, P, Pb, Sn, Sr, U, and Zn at the vein population are 5.87, 31.9, 54.85, 0.05, 1215, 7.26,200.30, 37,629, 10.8, 105.1, 3.01, and 15,867 ppm,whereas these values are 0.03, 0.96, 44.4, 0.05, 795.6,33.34, 512.4, 938, 7.19, 118.69, 1.2, and 1495 ppm at the background,respectively(Table 3).It is concluded that the vein, veinlet and brecciated zones are concentrated from Au,Ag,As,Pb,and Zn,while they were depleted from Nb and P (Table 3). The minimum and maximum Au at the vein population are 0.58 ppm and 14.85 ppm, where they are 0.00 ppm and 0.49 ppm at the background population,respectively. The half numbers of the vein samples are more than the median (3.69 ppm), while a quarter of samples numbers in this population are more than Q3(10.61 ppm).
The changes in the sum of trace elements (Au, Ag, As,Hg,Mn,Nb, P,Pb,Sn,Sr,U,and Zn)in background (126 samples) and vein (12 samples) samples are depicted in Fig. 7. Sum of the Au content in 12 samples that taken from veins is more than 70 ppm where, 126 samples from wall-rocks just show about 5 ppm.The sum of Au,Ag,As,Pb, and Zn content in vein and background samples indicates that Au and As are highly concentrated, Ag and Pb are concentrated, and Zn is rather concentrated in veins,compared to background values (Fig. 7).
6 Discussion
6.1 Interaction effects from optimized model

Fig. 7 The changes in the sum of trace elements(Au,Ag,As,Hg,Mn,Nb,P,Pb,Sn,Sr,U,and Zn)in background(126 samples)and vein(12 samples)samples.Sum of the Au content in 12 samples that taken from veins is more than 70 ppm where,126 samples from wall-rocks just show about 5 ppm
Organizing too many elements and a lot of models is so complicated that it could be facilitated by application of t test and the F test within BEA.When the model consist of first order,second order,and interaction terms of variables,it is so urgent to think carefully about elemental interaction terms that genetically derived from mineralization. Therefore,interactions were conducted by optimal RQM(Eq. 4)which obtained from multiple regression analysis and ANOVA within BEA.For this aim,Au is expressed versus two other elements (X1, X2) as Au(X1, X2), and other elements replaced with an average concentration of a normalized data which transformed to a positive interval(Doove et al. 2014; Samal et al. 2008). The Ag–Pb–Zn interactions on Au concentration were illustrated based on Ag–Pb, Ag–Zn, and Pb–Zn interactions in a graphical analysis. By replacing other elements equal to average values, Eq. 4 could be rewritten as Eq. 5.

To examine the interaction effect of Au (Ag, Pb) pairs,Zn was replaced by average value equal to 3 (the average value in all data is 3) then Eq. 5 rewritten as Eq. 6.

Therefore, the Au(Ag, Pb) interactions could reflect the elemental properties in vein and host rock populations.Where the Pb value changes from minimum (background population) to maximum (vein and veinlet population)values, and by devoting the desirable value of Pb at host rock and vein the Eq. 6 could rewritten as Eqs. 7 and 8,respectively.
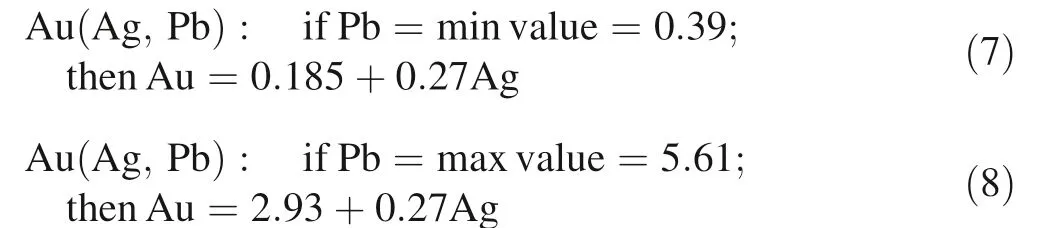

Fig. 8 Probability profiles of interaction effects of Au–Ag–Pb, Au–Ag–Zn, and Au–Zn–Pb from BEA of Au modelling (the units of the horizontal and vertical axis is the normalized data and the trend may be continued in some cases)
Graphical illustration of the Au(Ag, Pb), Au(Ag, Zn),Au(Zn,Pb)and Au(Pb,Zn)was depicted in Fig. 8 for two host rock (low level of concentration) and vein (high level of concentration)populations.The findings could reflect an important aspect of elemental changes in different populations.
Au (Ag, Pb): Au is regressed against Ag, when Pb limited to the host rock values. Accordingly, the variation trend of Au as a function of Ag is represented at Fig. 8a by a linear equation for the background population.Gradually increasing of Pb from host rock to vein values is accompanied by shifting the linear equation from the black to the red line. In this case, Pb variation cannot change the interaction between Au–Ag. Therefore, the double ordinal Au–Ag–Pb relationship is seen at both background and anomalous populations (Fig. 8a).
Au (Ag, Zn): Like as Pb, variation in Zn concentration from host rock to vein values also cannot change the interaction between Au–Ag,and it cannot cause significant changes in Au values. The results at Fig. 8b (Au–Ag–Zn)could suggest that Zn concentration at vein and veinlets would probably be closer to those observed in the host rock, as compared to Pb-related productive effects (Au–Ag–Pb; Fig. 8a).
Au (Zn, Pb): When the Pb level was maintained at the background value,an increase of Zn values causes a linear decrease in the Au concentration (Fig. 8c). In order to investigate the colinearity of Au–Zn, the gradual increases in Pb revealed that the black line is rotated anticlockwise.When the Pb level is equal to the maximum(vein)values,a positive linear relationship between Au and Zn is formed.Therefore, by concentration changes from the host rock to the vein, the negative slope reversed to positive in the linear interaction between Au, Pb, and Zn. This change indicates disordinal interaction of Pb–Zn on Au at the host rock (Fig. 8c). It can be concluded that we cannot assume that Pb was maintained at the minimum level, but Zn increases to the maximum values at the vein, veinlet and brecciated zones.Hence,an interaction effect between Pb–Zn pairs on Au indicates that Pb and Zn growth together in mineralization and this intergrowth was in order to increase of the Au concentration (Figs. 8c, 9a). The Akima linear interpolation was applied for dependency tracing between the Au–Zn–Pb datasets in Fig. 9a. At the vein,veinlet and brecciated zone a positive colinearity between Au–Zn–Pb is observed but in the host rock increase of Zn led to decrease in the Au. The best interaction effects of Pb–Zn on Au (which is occurs at Fig. 8c by two linear equations intersecting) is very sensible in Fig. 9a. Meanwhile, Pb is considered at the constant values, with a gradual increase of Zn the Au values increase on the y = x line.
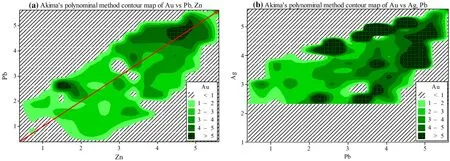
Fig. 9 Akima’s polynomial method contour map for Au–Pb–Zn (a) and Au–Ag–Pb (b) interactions
Au(Pb,Zn):There was a linear interaction between Au and Zn (Fig. 8c), but Au and Pb relationship can be expressed by a quadratic equation (Fig. 8d) according to Eq. (5). Whatever, Zn levels considered in veins, the quadratic equation shifted in order to increase Au and Pb values.
Afterward, the linear Au–Ag relationship is impressed with U contents.The high content of U shows a disordinal effect,while the U is remaining in the low content the Au–Ag linear equation show increases. Therefore, a disordinal interaction effect was obtained between Ag and U with respect to the Au content (Fig. 10; Au–Ag–U). As another example, the quadratic relationship of Au–Pb was transferred in order to increase Au concentrations, when U content is increased from low to a high level(Fig. 10;Au–Pb–U). It can be concluded that the low level of U concentration is associated from host rock samples.
Based on Akima’s polynomial contour map of Au–Ag–Pb,the highest Ag concentration overlay on maximum Au–Pb values from the vein, veinlet and brecciated zone samples (Fig. 11a). Therefore, with simultaneous increasing of Au and Pb, the highest Ag content can be obtained.Au–Pb variation shows the best interaction on Ag(Fig. 11a, like as Pb–Zn on Au at Fig. 9a), while there is not a clear trend for Au–Pb pairs on Hg concentrations(Fig. 11b). Whatever the maximum Hg contents were not overlay on vein and veinlets, the concentrated samples could be seen on adjacent sections above veins and brecciated zones at different levels. Accordingly, the highestHg contents are discovered at the low, intermediate and high Au–Pb values(Figs. 11b,12).Hence,Ag is correlated on Au–Pb values,but Hg is not correlated as well(Fig. 11).A graphical illustration of the Au–Ag–Hg based on Eqs. (4) indicates when the concentration of the Hg is restricted to the high level, the Au is concentrated rather than when Hg is at the low concentrations (Fig. 12a). On the other hand, Akima’s polynominal contour map of Hg versus Au–Pb indicates that Au–Pb have collinearity (setting on y = x) with Hg but not so good correlated(Fig. 11b). Good multicollinearity and correlation is seen in Fig. 11a, where Ag depicted versus Au–Pb and they are concentrated at the vein and veinlet and brecciated zones.Therefore, by comparison of Hg and Ag it was confirmed that they are not so correlated or interacted, and Hg was seen at a different range of Au–Pb values or not restricted to the vein or host rock (Fig. 11). This is verified by Au versus Ag–Hg in Fig. 12b,while a higher concentration of Au also accompanied by higher Ag values and the association of them encountered in the range of Hg from 2.3 to 5.61 in normalized data. Whatever, few samples were concentrated from Au and depleted from Ag and Hg.Therefore,Ag–Hg pair does not show an interaction effect on Au and the relationship between Au and Ag is also ordinal with respect to the Hg variation.
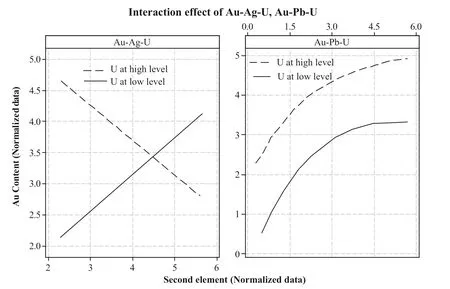
Fig. 10 Probability profiles of interaction effects of Au–Ag–U,and Au–Pb–U from BEA of Au modelling

Fig. 11 Akima’s polynomial method contour map of Ag–Au–Pb (a) and Hg–Au–Pb (b)

Fig. 12 Probability profiles of interaction effects of Au–Ag–Hg from BEA of Au modelling(a),and Akima’s polynomial method contour map(b)
6.2 Geological and geochemical verification
According to the linear relationship between Au–Ag mineralization from optimized QPM and interaction effects procedure, Zn variation indicates at least changes between the vein and host rock (Fig. 8b). By increasing Znconcentration from the minimum (host rock) to maximum(vein) values, a little increase was observed for Au concentrations.It was driven by the vertical shift of the line at Fig. 8b.On the other hand,there ares considerable changes in Pb concentration from host rock to the vein and brecciated zone (Fig. 8a). According to what is depicted in Fig. 8a and 8b, where Zn concentration restricted to the host rock, the Au(Ag, Zn) line show higher Au values,compared to the Pb values in Au(Ag, Pb). On the other hand, while Zn grows to the vein values the Au(Ag, Zn)line raise up but its increases are lower than Au(Ag, Pb)values. Therefore, changes in Pb concentration is more coordinated with Au.Finally,it was clearly shown that the concentration differences level of Zn is lower than Pb for the vein and host rock(Fig. 8a,b),which is verified by the concentration-depth profile in the BH2N1 for Pb and Zn at Fig. 13.

Fig. 13 Concentration-depth profile in the BH2N1 for Au,Pb and Zn
From the concentration differences level of Au, Pb, Zn(Fig. 13) and Ag (Fig. 14), it was found that the level of variation between the vein and host rock is known as Zn <Pb <Au <Ag (Figs. 13, 14). This trend of concentration changes can verify the results of modeling(Fig. 6), interaction effects (Fig. 8), and Akima’s polynomial method contour map (Fig. 9). Whatever, the maximum Zn contents are seen at the vein, but it is obviously that it was concentrated in the near surface zone and lithology (lower distance; Fig. 13).
Due to the Au, Ag, Pb, and Zn interactions in Fig. 8, it was found that they are concentrated in the veins, and all the restriction for the third-part element in the different environment indicates the highest colinearity between them. Individual Pb and Zn gradual changes indicate the linear relationship between Au and Ag (Fig. 8a and 8b).While the linear relationship and gradient of Au (Ag, Pb)and Au (Ag, Zn) are similar and stay fixed. The minimum Au values directly correspond to the minimum Pb concentrations and the highest Au values have been obtained by the highest range of Pb(Fig. 8a). Therefore,in contrast to the strong dependency of Au–Ag on Pb variation, it is moderate for Zn(Fig. 8).Perhaps it may conclude that the host rock contains higher concentration of Zn comparing to Au and Pb (Fig. 9). Therefore, Au and Ag show simultaneous occurrences, while Pb and Zn revealed such occurrences with high interaction effect during mineralization process(Figs. 13,14).Whereas,it is worth to be mentioned that Zn is a mobile element and may add in significant amounts to the host rock. Zn shows similar mobility with Pb, while in the near surface zone Zn has considerable mobility (Fig. 13).
The presented results are highly consistent with the Mehrabi et al. (2016) studies that indicate three stages of mineral assemblages in the Glojeh. The early (first) stage with Cu–Au–As–Sb–Fe mineralization;the second stage is Pb–Zn–Cu ± (Ag ± Cd) assemblages, and the third one was determined as the main dominated-hydrothermally sources of Au–Ag–(Bi–Pb). The Pb and Zn which highly interacted in the optimized model (Eq. 5), interaction studies (Fig. 8), and Akima’s polynomial method contour map (Fig. 9), originated from the second stage of mineralization, while Au and Ag simultaneous occurrences occurred during the third stage of mineralization. The galena, sphalerite,and sulfosalts were deposited at the 2nd stage of mineralization,are the main minerals that occurred by the Pb and Zn interactions. Finally, Pb and Zninteractions is an implication of intergrowth of Pb–Zn on Au concentration at the second phase of Pb–Zn–Cu ±(Ag ± Cd) sulfide mineralization.

Fig. 14 Concentration-depth profile in the BH2N1 for Au,Ag, Hg and Nb. Au and Ag are concentrated at the vein, veinlet and brecciated zone, while Hg changes not restricted to the vein and host rock. It tend to be increase at the depth of BH2N1 borehole. Nb considered as immobile element and depleted at the veins
In the present study, plots of the variation of Nb with Au, Ag, Pb, Zn, and Hg indicate that Nb is an immobile element (Fig. 14d). The concentration of the Nb was not varied due to hydrothermal alteration, therefore it can be selected to discriminate various rocks (Fig. 14d). Akima’s polynomial contour map of Nb versus Au–Ag show the higher Nb concentration associated with host rock samples that have lower Au–Ag concentration (Fig. 15). Hg concentrations appear to increase after 100-meter depth at the BH2N1 (Fig. 14c), and it may be related to a thick vein which may be intersected in further distance.Therefore,Hg indicates greater variability and do not correlate well with Au–Pb pairs (Fig. 11b), but Ag correlate good and indicates a good interaction effect on Au–Pb (Fig. 11a).
7 Conclusions
The results of this study demonstrate the advantages of using interaction effects to reveals the vertical quadratic dependency between elements and decrease the cost of Au analysis from modeling evaluation. The geochemical data processing results are:
1. In order to predict an optimized model, after eliminating 54 insignificant from 90 initial predictors, the R2(pred.) criterion increases from 0% to more than 77.80%.
2. The miniature changes in the model indicate, the Au(Ag,Pb)and Au(Ag,Zn)does not show an interaction effect.It implies that there is an interaction for Au(Zn,Pb).

Fig. 15 Akima’s polynomial method contour map of Nb versus Au–Ag
3. Au and Ag show simultaneous occurrences, while Pb and Zn revealed such occurrences with high interaction effect during the mineralization process. The Pb and Zn interaction is an implication of intergrowth of Pb–Zn on Au concentration at the second phase of Pb–Zn–Cu ± (Ag ± Cd) sulfide mineralization which suggested by Mehrabi et al. (2016) studies, while Au and Ag simultaneous occurrences originated from the third stage of mineralization. Zn shows similar mobility with Pb, while in the near surface zone Zn has considerable mobility. All the resulted interactions from QPM were confirmed by the Akima linear interpolation for dependency tracing between elements.
4. Nb occurs as the immobile element, while Hg indicates greater variability and does not correlate well with Au–Pb pairs in Glojeh polymetallic deposit. Hg may be restricted to upper section adjacent the vein and veinlets.
5. The polymetallic (Au–Ag–Pb) mineralization of Glojeh deposit may be associated with porphyry-style mineralization at depth.
AcknowledgementsThe authors are hugely thankful to Ms. Shima Allahyari for her encouragement and valuable help.
- Acta Geochimica的其它文章
- Acta Geochimica
- Correction to: A re-assessment of nickel-doping method in iron isotope analysis on rock samples using multi-collector inductively coupled plasma mass spectrometry
- Statistics matters in interpretations of non-traditional stable isotopic data
- Distribution and ecological risks of heavy metals in Lake Hussain Sagar, India
- Ecological risk assessment of surficial sediment by heavy metals from a submerged archaeology harbor,South Mediterranean Sea,Egypt
- Antimony removal from wastewater by sulfate-reducing bacteria in a bench-scale upflow anaerobic packed-bed reactor

