基于K-means算法识别瓦斯传感器软故障研究

胡 宇，周代勇

(1.瓦斯灾害监控与应急技术国家重点实验室，重庆 400037； 2.中煤科工集团重庆研究院有限公司，重庆 400039)

煤矿安全监测监控系统中瓦斯传感器是对煤矿井下瓦斯浓度进行采集，瓦斯传感器采集的数据是否是煤矿井下真实的瓦斯浓度与煤矿的安全问题息息相关[1]，因此，对瓦斯传感器进行软故障的研究具有重大的意义。对于瓦斯传感器软故障的故障情况，往往会出现瓦斯传感器漂移型(数据漂移)、偏置型(数据长期低于或高于正常值)、冲击型(数据出现大值)、周期型(数据周期性变动)等软故障[2-3]，能够有效地识别瓦斯传感器的软故障类型是为煤矿安全生产提供了一套实用技术手段。

到目前为止，传感器软故障的检测技术有基于解析数学模型的方法：参数估计法，状态估计法和等价空间法[4]，优点是模型机理清晰，结构简单，易实现，易分析，可实时诊断。缺点是计算量大，系统复杂，存在建模误差，模型的适应性差，可靠性差，容易出现误报、漏报等现象，外部扰动的鲁棒性，系统的噪声和干扰不敏感。不依赖于数学模型的软故障方法有基于数据驱动的方法，基于知识的方法和基于离散事件的方法，优点是不需要对象的准确模型，并且适应性强，其缺点是结构复杂，难于实现[5-6]。针对煤矿井下瓦斯传感器设备安装位置、运行环境复杂多变等特点[7]，以及煤矿安全监测监控系统中瓦斯传感器采集到数据记录和瓦斯传感器设备的运行情况。本文提出了一种轮廓系数自适应最佳聚类点的K-means算法检测瓦斯传感器设备软故障监测方法。该方法是利用聚类中心点的迭代循环计算出最优中心点，选择最佳聚类点再进行K-means聚类。同时结合RBF神经网络算法对故障瓦斯传感器特征能量谱作为输入，进行自适应最佳聚类点的K-means算法分类训练，就能够确定运行的瓦斯传感器出现软故障状态情况。

1 设备软故障信号小波包分析

1.1 软故障信号小波包分解

小波包分解是对信号进行有效的时频分解，其尺度函数是按二进制变化的，高频段进行指数等间隔划分，低频段做进一步分解，能够更加精细地表征低频信号。因此小波包分解能够自适应地对高频信号按照信号自身的频段进行细化信号的特征，细化后的信号频率完全与信导频率是相符合的，小波包分解是提升了信号的时频分辨率[8-9]。小波包分解存在具体如下关系：

S=AAA3+DAA3+ADA3+DDA3+AAD3+

DAD3+ADD3+DDD3

(1)

1.2 软故障信号特征量提取

小波包分解是一种信号频率越高，分解率较高的信号分解算法，其中有φ(t)尺度函数，ψ(t)为小波函数，定义正交尺度函数确定函数簇，生成小波库。

(2)

hk、gk分别为低通滤波器与高通滤波系数，小波包分解和重构递增公式为：

(3)

(4)

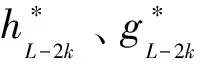
(5)

式中：djk—重构信号DNj的第k个离散的幅值；n—重构信号DNj的离散点个数，j=0,1,…,2N-1,k=1,2,…,n。将获得各频带信号能量的特征向量作为RBF神经网络的训练样本输入。

2 K-means聚类算法的RBF神经网络训练

2.1 K-means聚类算法

K-means算法是利用质心与质心之间的距离迭代，选择最优质心距离来进行聚类划分的算法，当类间质心点的距离相互收敛时，算法质心的距离迭代结束，聚类计算分辨出具有共同特性的类别[10]。优点是算法实现简单快捷，数据大小可伸缩，计算数据类高效。缺点是算法对初始距离质心点依赖性大，初始质心点的偏差可能导致产生的结果偏离实际的分类，算法在运行时需要不断地更改类质心距离，数据计算量比较大，算法开销的时间也比较大，聚类的种类是预先设定的，很难估计[11]。

针对K-means算法存在的缺陷，本文对K-means算法随机初始聚类质心点距离进行改进，利用轮廓系数对个体样本进行聚类点距离缩小，类质心点轮廓系数距离进行扩大，样本轮廓系数和类质心点轮廓系数定义为Si和S，其中与距离关系为：

(6)

(7)

上述两公式中,当样本i∈C类时，x(i)表示个体样本i和同属C类其他个体样本到类质心点的平均距离，当样本i∉C类时，y(i)表示个体样本i到其他非C类个体样本的距离最小值，个体轮廓系数Si是用于评价样本聚类到相应种类的适合度，故Si为[-1,1]，当Si越接近1时，该样本到类质心距离就越小，样本的归属于该类的可能性就越大，n为样本总数，核心指标为误差平方和SSE：

(8)

式中：Cj—第j个簇；p—Cj的样本点；mj—Cj的质心；SSE—所有样本的聚类误差代表聚类效果的好坏，具体的算法步骤如下：

1)设定参数M,初始化j=1,当jM时，完成下列循环：

a.调用随机初始聚类的质心点完成初步K-means算法分类；

b.初始聚类后，计算各个样本到C类质心点的距离矩阵D(j)c(c=1,2,…,K);

c.调用个体轮廓系数公式计算相应的个体轮廓系数Si(j);

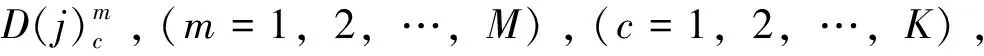
3)对优秀样本进一步求取均值，利用求取后的均值作为聚类中心，再进行K-means聚类。

2.2 基于RBF神经网络训练

RBF神经网络训练算法是一种逼近任意非线性函数的训练方法，具有很快的非线性学习收敛特点，适合用于故障诊断技术中[12-15]。学习步骤如下：

1)确定基函数中心CP

瓦斯传感器软故障时产生了故障能量特征值作为输入样本，用上述优化K-means聚类算法求出输入样本的各类中心，作为径向基函数的中心[11]。

2)径向基函数的宽度δP

基函数宽度是采用K-means聚类算法聚类的结果，即各个样本到聚类质心点的平均距离为基函数宽度，δi(i=1,2,…,I)表示I个基函数的方差，其宽度为：

(9)

式中，dmax表示选择的中心两两之间的距离最大值。

3)权值wp

输出层权值线性方程表示为：

y(xi)=w1φ1(||xi-X1||)+

w2φ2(||xi-X2||)+…+

wpφp(||xi-Xp||)

(10)

每个样本的期望输出为d数组：

(11)

所用样本为：

(12)

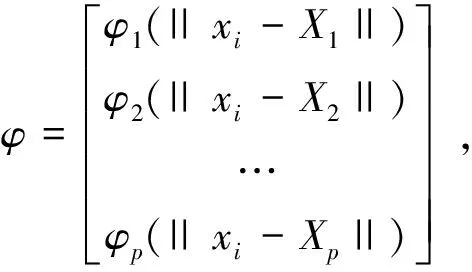
(13)

3 实验验证与分析

3.1 实验配置

实验以贵州土城煤矿为实验对象，从土城煤矿监控系统瓦斯数据库获取瓦斯传感器5种状态下的数据各80组。对各种状态的瓦斯数据进行小波包分解处理重构，利用小波包的相关算法提取信号的特征能量谱，组合成向量作为神经网络的输入样本，瓦斯传感器各种状态下的特征能量谱样本如图1所示。

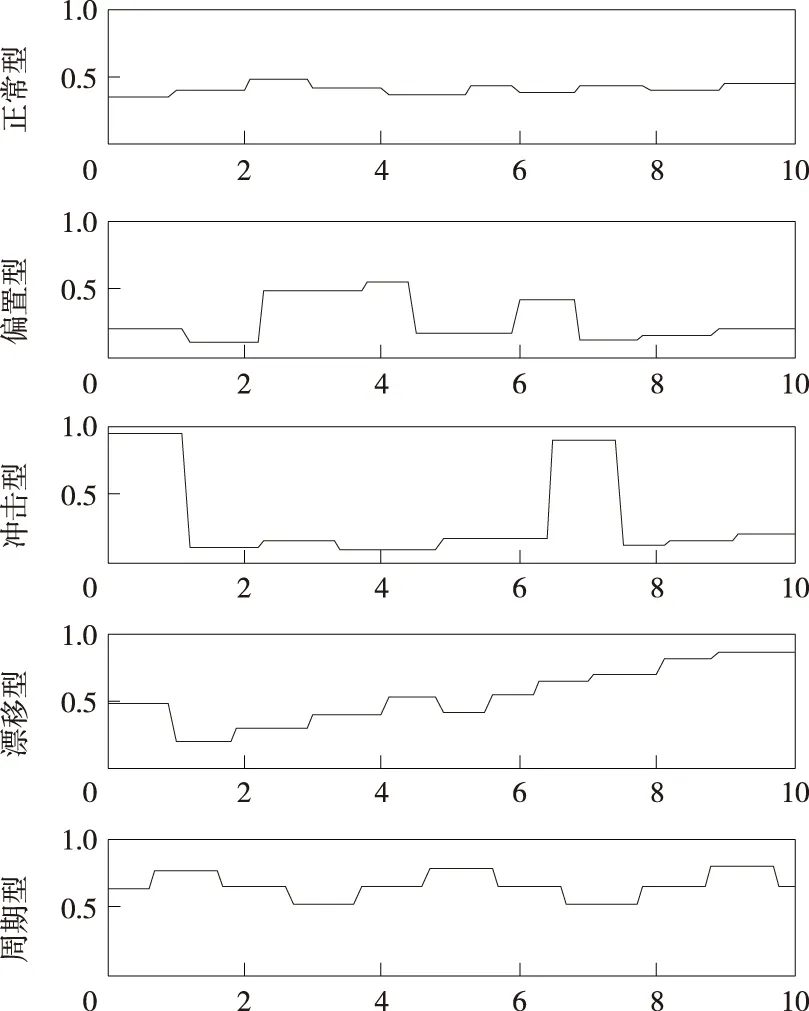
图1 瓦斯传感器设备5种状态下的特征能量谱Fig.1 Characteristic energy spectrum of the gas sensor device in five states

对自适应聚点K-means算法进行RBF神经网络训练。RBF神经网络输出层节点为3，是由于瓦斯传感器设备运行时运行状态细化为5种，映射关系具体对应关系如表1。因此可以确定网络输出节点为3。输入层节点为8，是由于小波分解的特征能量谱向量来确定。隐含层的节点是自适应聚点K-means算法特点可确定为5。RBF神经网络采用8-5-3结构。通过提取特征向量组成样本，进行RBF神经网络训练。

表1 瓦斯传感器运行状态与神经网络输出关系Table 1 Relationship between the operating status of the gas sensor and the output of the neural network

3.2 实验验证

从土城煤矿监控系统瓦斯数据库中取出软故障状态的数据各20组，分别对取出的数据进行测试。对神经网络算法训练的结果，进行实验验证如图2所示，可以从图中看出，100组样本通过自适应聚点K-means算法识别的瓦斯传感器故障分为5类。表2中看出，故障状态传感器识别率高达95%。因此，该自适应聚点K-means算法可以有效地识别瓦斯传感器软故障的类型，同时识别率能够达到预期的设计效果。

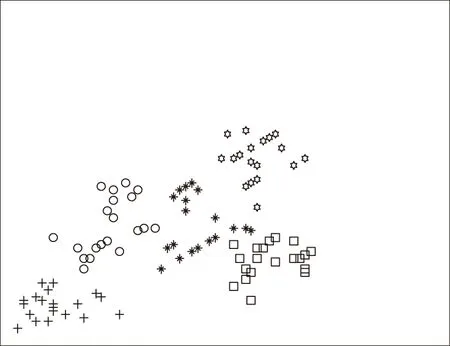
图2 样本识别分类结果Fig.2 Sample recognition classification results

表2 实验输出结果Table 2 Experimental output results

4 结论

1)利用小波包对瓦斯传感器软故障信号进行分解，分解算法降低了软故障信号的特征能量谱的向量维数，更好地体现出软故障时的特征信号，小波包分解是一种很实用的故障信号波形处理方法。

2)加入轮廓系数的K-means聚类算法，自适应地优化了聚类中心点，使得聚类效果更加明显，瓦斯传感器软故障识别率高达95%。该算法运用到监控系统中不仅能够提高瓦斯传感器设备运行的可靠性，而且也提高了煤矿安全监控系统的准确性。