Kinetic simulation of an electronegative plasma with a cut-off distribution and modified Bohm criterion
Suresh BASNET and Raju KHANAL
Central Department of Physics,Tribhuvan University,Kirtipur,Kathmandu 44613,Nepal
Abstract
Keywords:Bohm condition,kinetic simulation,plasma–wall interaction,electronegative plasma
1.Introduction
Study of the plasma–wall interaction mechanism is of considerable interest as it has wide range of growing applications including in divertors of fusion device,plasma etching,sputtering,chemical vapor deposition and many more [1–4].The formation of a non-linear plasma sheath in the immediate vicinity of the material wall or electrode and its characteristics determine the flow of particles,the impact energy of projectiles and heat flow,which in turn affect the lifetime of plasma-facing materials (PFMs) used in fusion devices.Therefore,appropriate design of the divertor wall along with material selection is very important [5–7].In a plasma with negative ions (e.g.H-,O-),often called an electronegative plasma,the presence of negative ions can significantly affect the characteristics of the plasma sheath as these differ from electrons in mass,thermal velocity,mobility and energy[8,9].Much research has also been devoted to multi-component plasma–wall interactions,in both the absence and presence of negative ions,in the presence of two temperature groups of electrons [10–14].The presence of a second ion species (positive or negative ions) in a multi-component plasma affects the sheath characteristics,namely potential function,sheath thickness and energy flow towards the wall.In the past few decades,the study of plasma–surface transition in an electronegative plasma has become an area of interest both experimentally and theoretically [15–20].The electrostatic potential distribution is a monotonic function in the sheath region.The pre-sheath–sheath structure and its characteristics,such as floating potential and sheath thickness,are governed by the negative ions instead of electrons.Also,it is reported that the electric field in the sheath region has a stepwise structure due to reflection of negative ions [21,22].
Experimentally,Sarma et al [23] studied a steady state multi-component plasma with negative ions and found that the presence of negative ions affects the sheath structure and obeys the modified Child–Langmuir law.Yasserian et al[24]investigated an electronegative discharge in the presence of a constant uniform magnetic field,whose strength also determines the nature of the particle density profile,potential distribution and the velocity of positive ions.When an intermediate magnetic field is present in an electronegative plasma,the electric potential has oscillatory structure; while for strong magnetic field,these oscillations vanish.Stamate[25] studied the charge distribution on the surface of biased electrodes in the presence of negative ions by simulation and experiments.The discrete and model focusing effects were identified and discussed.Discrete focusing is concerned with the formation of a passive surface whereas model focusing is concerned with the formation of a certain model line or model spots.Crespo et al [26] examined the positive ion sheath formed around a cylindrical electrode and its transition from electropositive to electronegative behavior.The concentration of negative ions and temperature affect the potential distribution and sheath thickness.

Figure 1.Schematic geometry of a magnetized plasma sheath in which ∣∣v and ⊥v are the parallel and perpendicular velocities with respect to the magnetic field.
The present work is concerned with the properties of an electronegative magnetized plasma sheath,which is crucial in industrial applications of plasma,for example semiconductor fabrication and dry etching.In order to study the plasma–wall interaction process,we employ the kinetic trajectory simulation(KTS)method to solve the related kinetic equations.The fundamental kinetic Bohm condition for the formation of a stable plasma sheath has been derived for the case of an electronegative magnetized plasma.Moreover,the obtained results have useful applications such as in modeling of the divertor wall in a fusion device,generation of a negative ion beam source and sputtering.
2.Kinetic model and basic equations
The kinetic modeling of various situations of interest yields results of high accuracy compared with the fluid approach[27],and in the KTS method the characteristics of spatially bounded plasma are studied following an iterative scheme[28].A fundamental element of KTS is to trace the particle trajectories in the phase space to discover the related ion velocity distribution functions.In order to trace the trajectories,the simulation region is discretized and the ion equation of motion is solved in a time-centered manner[28–30].An initial potential distribution and particle distributions are taken as input to the iteration and the governing kinetic and the Maxwell equations are solved self-consistently for prescribed boundary conditions.Further detail about discretization and the KTS method is given in our previous work [31].
The geometry of the magnetized plasma sheath is shown schematically in figure 1,and the plasma consists of singly charged positive ions,negative ions and electrons.Our simulation region lies between x = 0 (the plasma-facing electrode or wall)andx=xp(the bulk plasma boundary from where plasma particles flow towards the wall or electrode).The external applied magnetic field B acts in the x–z plane which makes an angle ψ with the normal to the material wall.The simulation region is considered to be 10 electron Debye lengths,which is smaller than the collision mean free path so that the simulation region is assumed collision free.The positive ion velocity distribution function at x = xpis assumed to be Maxwellian,such that the quasineutrality of plasma at the sheath entrance,continuity of physical parameters and the kinetic Bohm sheath criterion are all satisfied at the pre-sheath–sheath boundary.In addition,for smooth flow of the plasma parameters between pre-sheath–sheath boundary,we use the 1d3v coupling scheme that couples the pre-sheath side fluid parameters with kinetic sheath parameters [31].For a collisionless plasma,the Boltzmann equation becomes the Vlasov equation,which for the timeindependent case is
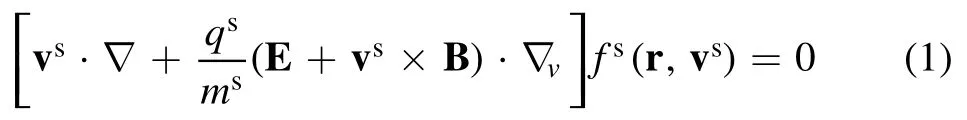
in which ms,qsandfs(r ,vs) are the mass,charge and the distribution function of the particle species s,respectively,and the termis the macroscopic acceleration of particle species s.
The space charge density is calculated as

and the electric field is calculated as

in which the electrostatic potentialφ(r) satisfies the Poisson equation

where є0and nsare the electric permittivity for free space and density of particle species s,respectively.
The positive ion velocity distribution function at x = xpis considered to be

As the wall will be at negative potential,its reflective nature causes the electron and negative ion distribution functions to be cut-off Maxwellians as


npssis the density of particle species s at the pre-sheath–sheath interface,kBis the Boltzmann constant,is the thermal velocity,Tsis the temperature of particle species s,Θ(x) is the Heaviside step function,is the cut-off velocity at position x,φwis the wall potential andvxim(xp)is the Maxwellian maximum velocity of ion at x = xp.
The density of particle species s at the pre-sheath–sheath boundary is calculated as

which yields

and

The average fluid velocity of particle species s at the presheath–sheath interface is

such that

where

and

where

and i is the unit vector along the direction of motion of the particles.
The temperature distribution of particle species s is

which yields

and

The cut-off density distributions for electrons and negative ions are

2.1.Kinetic Bohm condition for electronegative plasmas
A stationary non-neutral plasma sheath is formed only if the ion speed at the sheath entrance satisfies the Bohm sheath condition,which implies the ions must enter from the sheath entrance with sufficiently high speed.The Bohm criterion is not considered to be a physical law as it sometimes requires a few modifications because it depends on the ion velocity distribution at the pre-sheath–sheath boundary [32].In this section,we extend and derive the generalized kinetic Bohm criterion for the electronegative plasma,which ensures the formation of a positive space charge region near the material wall.The generalized Bohm sheath condition for such an electronegative plasma can be written as

which yields


Table 1.Physical parameters and simulation conditions.
With the assumption of a Maxwellian distribution of electrons and negative ionsthe kinetic Bohm condition equation (25) becomes

Equation (26) is the well-known Bohm condition for an electronegative plasma [33].In the absence of negative ions,i.e.δ = 0,equation (25) becomes

in whichis the normal component of fluid velocity at the magnetic pre-sheath entrance.Equation (27) is a kinetic Bohm sheath condition in the presence of cut-off Maxwellian electrons,which is similar to the previous work [34].
3.Results and discussion
For the numerical stability of the kinetic simulation,we adopt the stability conditions as

and

where△xis the mesh size,λDeis electron Debye length,△tis the numerical time step of the simulation and ωpeis the electron plasma frequency.The condition for the convergence check at each point is

in whichφ m(xk)andφm-1(xk)are readjusted new potential and old potential distributions,respectively,with Δφ defined as an accuracy parameter.
To solve the compiled basic kinetic equations,the physical parameters and simulation conditions considered are shown in table 1.
The parallel and perpendicular positive ion velocity distributions at the particle injection sidex=xpand at the wall x = 0 are shown in figure 2.It is seen that both the distributions are half Maxwellian at the injection side and at the wall.The parallel distribution has a higher Maxwellian maximum velocity (0.863vtiin figure 2(a)) than the perpendicular distribution (0.487vtiin figure 2(b)) at the injection.The magnitude of this Maxwellian maximum velocity of the distributions increases at the wall and the increment is higher for the parallel distribution,as depicted in figures 2(c) and (d).At the entrance side,the ions have different velocities with which they follow the trajectory and enter into the sheath region.The (x,vx) phase-space diagram for positive ions is shown in figure 3.
The presence of negative ions in the plasma reduces the Bohm velocity of positive ions,which is a necessary condition for the formation of a stable plasma sheath.The kinetic Bohm velocity with and without cut-off distributions is shown in figure 4.When the concentration of negative ions is very low and we assume a Maxwellian distribution of particles without cut-off in the electronegative plasma,the marginal Bohm criterionuni,SE≥csmust hold while the criterion for a cut-off distribution isuni,SE≥0.995 8cs.The Bohm velocity at the magnetic pre-sheath entrance decreases with increase in concentration of negative ions and exhibits a qualitatively similar nature for both cases.However,the adoption of cut-off distributions causes the modified Bohm velocity to deviate compared with the original case defined by equation (26); it differs by 1% in magnitude.
The variation of the self-consistent electrostatic electric potential profile in the plasma sheath region for three different concentrations of negative ions (δ = 0.00,δ = 0.25 and δ = 0.67)is shown in figure 5.It is found that the magnitude of electric potential increases towards the wall in all cases and their slopes also increase towards the wall.The effect of negative ion concentration increases away from the sheath entrance,which is seen clearly in the inset in figure 5(a).The bulk plasma always tends to preserve the quasineutrality property; however,there is always change in the potential profile near to the wall.The magnitude of the potential decreases with the increase in concentration of negative ions as it reduces the concentration of mobile electrons.The obtained potential profile for the case of δ = 0.00 is qualitatively similar to a previous work[28].In order to have clear visualization of the increment in magnitude of the potential towards the wall,the potential at different grid points is shown in figure 5(b).In this figure,the heights of potential at 41 and 1 grid points represent the particle injection side and wall,respectively.It is clearly observed from figure 5(b) that the height of potential is maximum at the wall and minimum at the pre-sheath–sheath boundary.Therefore,the electric field has a weak influence at the pre-sheath–sheath boundary while its effect goes on increasing towards the wall.Due to the strong influence of electric field near the wall,the particles strike the wall normally.In this case the motion of particles in the sheath region is dominated by the electric force rather than the magnetic force as depicted in figure 6.The electric force starts to dominate over the magnetic force from about 4 Debye lengths from sheath entrance.

Figure 2.Positive ion distribution at constant concentration ratio δ = 0.25(a)and(c)parallel to the magnetic field at injection and at the wall,respectively (b) and (d) perpendicular to the magnetic field at injection and at the wall,respectively.

Figure 3.1d1v phase-space trajectories of positive ions.

Figure 4.The kinetic Bohm velocity with cut-off (red dashed line)and without cut-off (blue solid line) as a function of the concentration of negative ions.
The particle density profiles at constant concentration ratio δ = 0.25 are shown in figure 7.The density of all charged particles decreases towards the wall; however,the density of negatively charged particles decreases much faster than that of positive ions.The density of positive ions at the wall is 0.476npswhereas the densities of electrons and negative ions aren0.021psandn0.0012ps,respectively.Moreover,the density of positive ions reaching the wall is higher than that of negatively charged particles,which explicitly indicates that the space charge density has its maximum value at the wall and shields the effect of wall potential.
The negative wall potential retards the flow of negatively charged particles towards the wall,and hence both the average fluid velocity and thermal mobility decrease.The electrons have a lower mass than that of the considered negative ions so that the rate of decrease of average velocity is higher for negative ions.Thus,the electrons reaching the wall are more highly energetic than the negative ions,which is clearly observed from figure 8 which depicts the temperature profile of electrons and negative ions in the sheath region.The temperature has a non-uniform distribution and it decreases towards the wall.The temperature of electrons at the presheath–sheath boundary is 30 eV,which goes on decreasing(from figure 8(a)) towards the wall and is about 24 eV at the wall.Furthermore,from figure 8(b) it is seen that the temperature distribution of the negative ions decreases from 20 eV to about 16 eV.
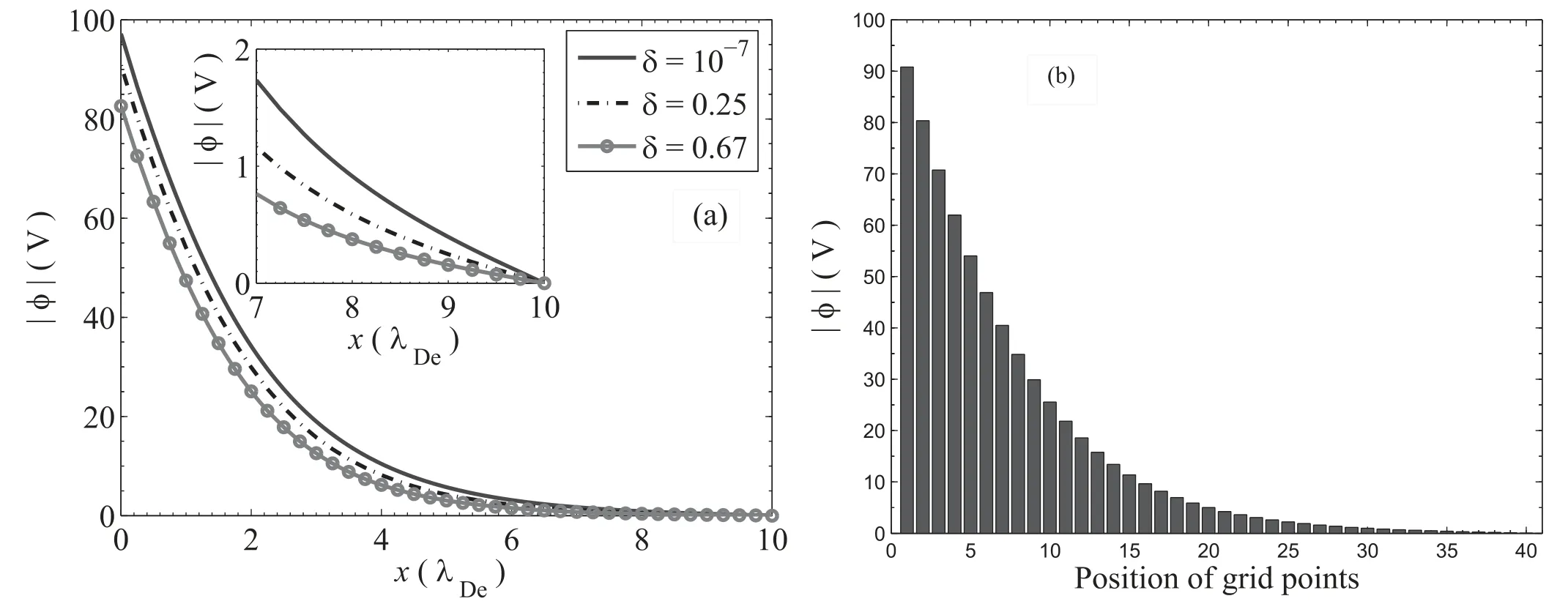
Figure 5.(a) Electrostatic potential distribution in an electronegative plasma sheath for different concentrations of negative ions.(b) The height of the potential at different grid points for a constant concentration ratio δ = 0.25.

Figure 6.Profile of electric (red dashed line) and magnetic (blue solid line) forces in the sheath region at a constant concentration ratio δ = 0.25.
To understand the plasma–wall interaction,the energy profiles of charged particles when the charged particles hit the solid first material wall have a crucial role.The energy profile of charged particles in the electronegative plasma sheath region is shown in figure 9.The striking energy of positive ions at the wall increases as they move towards the wall,but in the case of negatively charged particles the energy flow towards the wall decreases and the energy transferred by electrons is higher than that transferred by negative ions,as shown in figures 9(a) and (b),respectively.
4.Conclusions

Figure 7.Profiles of positive ion,electron and negative ion densities.
A kinetic simulation method was used to study the plasma–wall interaction when plasma consists of singly charged positive and negative ions and electrons.It was assumed that electrons and negative ions have cut-off Maxwellian distributions and the plasma sheath was collisionless as the mean free path is much larger than the sheath scale.The fundamental Bohm criterion for the formation of a stable positive sheath was derived in the case of electronegative plasmas.The magnitude of the kinetic Bohm velocity with and without cutoff distributions qualitatively agreed,although the results differ by about 1%.The presence of an oblique magnetic field in the plasma has significant effect on the distribution of ions at the sheath entrance and at the wall.It was found that the electrostatic potential shows monotonic variation in the sheath region,exhibiting a sharp gradient near the wall that affects the motion of charged particles.The motion of charged particles near to wall was highly influenced by the electric force rather than the magnetic force.The particle densities decreased towards the wall,the rate of decreasing of negative ions being much faster than that of positive ions and electrons.Furthermore,the energy transferred by the positive ions through the plasma sheath is greater than that of negatively charged particles.The present study has useful applications in modeling of divertor walls and sputtering that determine the lifespan of plasma-facing components.

Figure 8.Temperature profiles for (a) electrons (b) negative ions at a constant concentration ratio δ = 0.25.

Figure 9.Energy profile of particles in the sheath region at a constant concentration ratio δ = 0.25.
Acknowledgments
Suresh Basnet would like to acknowledge the University Grants Commission,Nepal for the PhD fellowship.
 Plasma Science and Technology2020年4期
Plasma Science and Technology2020年4期
- Plasma Science and Technology的其它文章
- Study on influencing factors of ion current density measurement in corona discharge of HVDC transmission lines
- Trap distribution of polymeric materials and its effect on surface flashover in vacuum
- Improvement of the electrical resistivity of epoxy resin at elevated temperature by adding a positive temperature coefficient BaTiO3-based compound
- Controlling fine particles in flue gas from lead-zinc smelting by plasma technology
- Suppression of a spontaneous dust density wave by modulation of ion streaming
- An investigation of the L-shell x-ray conversion efficiency for laser-irradiated tin foils
