三维柱体上调和方程的二择一结果

李远飞,石金诚,曾 鹏

(广东财经大学 华商学院，广东 广州 511300)

在1856年，SAINT-VENANT A J C B DE[1]提出了一个著名的数学和力学原理.原理一经提出就引起了在应用数学领域内广泛的研究，此原理后来被称为Saint-Venant原理.有关Saint-Venant原理的早期研究成果主要集中在椭圆方程的初边值问题上.Boley[2]最早指出Saint-Venant原理对热传导方程仍然有效.自此之后，各种类型的抛物方程受到了广泛的关注，比如Brinkman方程组、Navier-Stoke方程组、Darcy方程组、Forchheimer方程组和Boussinesq方程组等，详见文献[3-11].

上述文献大多假设在柱体的无限端方程的解趋近于零，从而得到方程组的衰减结果.经典的二择一定理不必假设方程组的解在无限端趋近于零, 而是证明调和函数随距有限端的距离的增大要么呈指数(多项式)增长要么呈指数(多项式)衰减.大多数文献通常假设柱体的母线平行于坐标轴，柱体任何一处的横截面都是相同的.笔者主要研究调和函数在一个半无穷柱体上的渐近性质，其中在柱体的侧面上满足零边界条件，在柱体的有限端满足非线性条件.注意到文献[12]考虑了3种不同的无界区域，通过推导一个二阶微分不等式，从而得到二维双调和函数在一个无界区域上的二择一结果.受文献[12]的启发，与大多数文献不同的是，假设柱体的横截面的面积不再是一个常数，而是与横截面的位置有关.当横截面的面积满足一些特定的条件时，得到了三维调和函数在3种不同半无穷柱体上的二择一结果.目前，出了文献[12]之外几乎还没有文章关注此类问题，显然，当前文献中所取得的结果是本文的一个特殊情况.

1.准备知识

令R表示三维区域上的半无限的柱体，Dz表示R在x3=z处的横截面，D表示R坐标平面x1Ox2上的横截面上，即

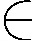
令∂Dx3表示Dx3的边界，z是x3轴上的一个动点，Rz分别记为

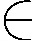
其中，Dx3是和x3相关的一个光滑区域.显然，R0=R,D0=D.研究定义在R×(0,∞)上的调和方程

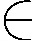
(1)

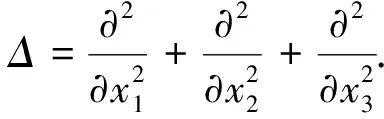
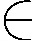
在柱体的边界上，有

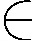
(2)

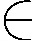
(3)

其中，g(x1,x2)是大于零的可微函数，且满足约束条件：

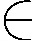
为了证明本文的主要结果，列出一个接下来常用的微分不等式.

引理1 若ω|∂Dz=0，则存在一个依赖于区域Dz大于零的函数r(z)数使得

其中，r2(z)=|Dz|表示区域Dz的面积.

证明设P是Dz内的一个点.令P1和P2分别表示过点P平行于x1坐标轴的直线与∂Dz的交点，令Q1和Q2分别表示过点P平行于x2坐标轴的直线与∂Dz的交点.由于|ω|∂Dz=0，所以

于是

(4)

同理

(5)

结合式(4)和(5)并利用不等式

2ab≤a2+b2a,b>0，

可得

由Hölder不等式，可得

证毕.

2 “能量”表达式的定义

为了推导本文的二择一结果，需首先推导“能量”表达式的定义.为此，从以下恒等式开始推导

其中，z0≥0是x3轴上的某个点，且z0≤ξ≤z.现使用散度定理，并利用方程(1)～(3)，有

(6)

若定义

(7)

则由式(6)可得

(8)

对式(8)微分，可得

(9)

使用Hölder不等式、算术几何平均不等式和引理1，由式(7)可得

再注意到式(9)，可得

(10)

由式(10)可以得到以下2个不等式

(11)

(12)

对2个不等式进行分析，从而得到二择一定理.

3 二择一定理

Ⅰ 半无穷柱体

如果区域Dz的面积是一个常数，即r(z)=r>0.对式(7)所定义的E(z)，利用式(11)和(12)作2种分析.

情形1 如果一个点z0>0，使得E(z0)>0.

由于E′(z)≥0，所以E(z)≥E(z0)>0，z≥z0>0.因此由式(11)可得

(13)

对式(13)从z0到z积分，可得

(14)

联合式(8)和(14)，可得

(15)

情形2 如果对所有的z≥0，都有E(z)≤0.

由式(12)可得

(16)

对式(16)从z0到z积分，可得

(17)

式(17)表明当z→∞时-E(z)指数式衰减于零.现对式(9)从z到∞积分，可得

(18)

又由于E′(z)≥0，所以-E(z0)≤-E(0).结合式(17)和(18)，可得

(19)

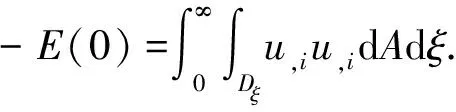
由上述分析可以得到定理1.

定理1设u为问题(1)～(3)在一个半无穷柱体R上的解.则要么

成立，要么

Ⅱ 扩展区域

如果柱体的界面Dz和z有关，则Dz的面积随z的变化而变化.例如，

在此种区域上，假设Dz的面积r(z)满足

r(z)≤δzγ0<γ<1，δ>0,z≥0.

(20)

分2种情形进行分析.

情形1 如果一个点z0>0，使得E(z0)>0.

由于E′(z)≥0，所以E(z)≥E(z0)>0，z≥z0>0.因此由式(11)可得

对上式从z0到z积分，可得

即

(21)

情形2 如果对所有的z≥0，都有E(z)≤0.

由式(12)可得

对上式从z0到z积分，可得

(22)

由于0<γ<1，所以当z→∞时-E(z)指数式衰减于零.与式(19)类似，得到

由上述分析可以得到定理2.

定理2设u为问题(1)～(3)在一个半无穷柱体R上的解，且柱体的截面Dz的面积r(z)满足式(20).则要么

成立，要么

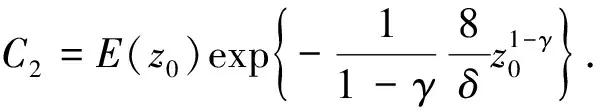
特别地，如果在式(20)中γ=1，则式(10)可以写为

对上式作类似的处理，易得定理3.

定理3设u为问题(1)～(3)在一个半无穷柱体R上的解，且柱体的截面Dz的面积r(z)满足式(20)但是γ=1.则要么

成立，要么

Ⅲ 一般区域

假设柱体R在x3=z处的横截面Dz的面积函数r(z)满足下列性质

r(z)≥r0>0z≥0，

(23)

再次对式(11)和(12)进行分析.

情形1 如果一个点z0>0，使得E(z0)>0.

由于E′(z)≥0，所以E(z)≥E(z0)>0，z≥z0>0.因此由式(11)可得

对上式从z0到z积分，可得

即

(24)

情形2 如果对所有的z≥0，都有E(z)≤0.

由式(12)可得

对上式从z0到z积分，可得

(25)

由于r(z)满足式(23)，所以当z→∞时-E(z)指数式衰减于零.利用式(18)并结合式(25)，有

由上述分析可以得到定理4.

定理4设u为问题(1)～(3)在一个半无穷柱体R上的解，且柱体的截面Dz的面积r(z)满足式(23).则要么

成立，要么

成立.

4 全能量-E(0)的上界

在衰减的情形下，由式(7)和(18)可知，

(26)

现定义一个辅助函数

S(x1,x2,x3)=g(x1,x2)exp(-σx3)，

其中，σ是一个大于零的常数.显然S(x1,x2,x3)与u具有相同的边界条件，所以利用式(1)可得

利用Hölder不等式、算术几何平均不等式

再结合式(26)，可得

注意到的定义，可得

5 结束语

研究了3种不同柱体区域上的调和函数的二择一问题.目前文献对本文所研究的问题的关注还比较少，这是需要考虑的一个新方向.此外，可以研究更加复杂的抛物方程组，希望本文的研究能带来一些灵感.同时，笔者也注意到文献[13]在柱体的侧面上施加了非线性边界条件(这类问题主要产生于稳态的热传导理论)，得到了调和方程的二择一结果.受文献[13]的启发，也可以假设在柱体的侧面上满足非线性边界条件，推导二择一结果.