基于MATLAB对转向力矩波动的应用研究

张学斌

摘 要：文章提出一种基于MATLAB数值分析方法，对汽车转向系统的力矩波动进行理论计算的思路和方法。并针对整车人机四向调节的转向管柱布置，能够较为准确的确定布置硬点。

关键词：数值分析;四向调节;力矩波动

Abstract： In this article， a numerical analysis method based on MATLAB is proposed to calculate the torque fluctuation of automobile steering system. According to the four-way steering column arrangement of the vehicle， the hard point can be determined accurately.

前言

在对汽车产品的研发工作中，整车性能指标贯穿始终，它的好坏直接影响成败。其中，在转向系统的开发中，除常规的转向助力调校之外，其它人机使用的需求也随用户的感知提升，内容也越来越丰富，比如由传统不可调转向管柱，逐渐发展为两向调节、四向调节。而一般主机厂为了控制成本，对转向中间轴总成两端的十字传动节叉常采用不等速万向节传动，使得设计上必须考虑转向力矩的波动，特别是角度调节范围对力矩波动的影响，从而带来更好的驾驶感觉，达到更优的性能指标。

确切地说力矩波动属于机械原理的范畴，其从理论上计算，存在计算量大、易出错，且在计算中变量值--相位角难以实现其范围变化，来确认最佳的设计值。这样会造成力矩波动过大的问题难以在设计初期暴露出来，往往在后期需要做设计变更时，付出的代价巨大。

在实际工作中为了优化转向力矩波动，确认最佳的传动相位角，我们可以借助MATLAB数值计算软件来实现对角度波动的仿真，以便对相关参数进行轻松变换和性能优化对比。

1 转向力矩波动产生的原因分析

1.1 单万向节不等速传动概述

十字轴万向节从动节叉与主动节叉转角间的精确表达式为：

1.2 单万向节不等速传动原理

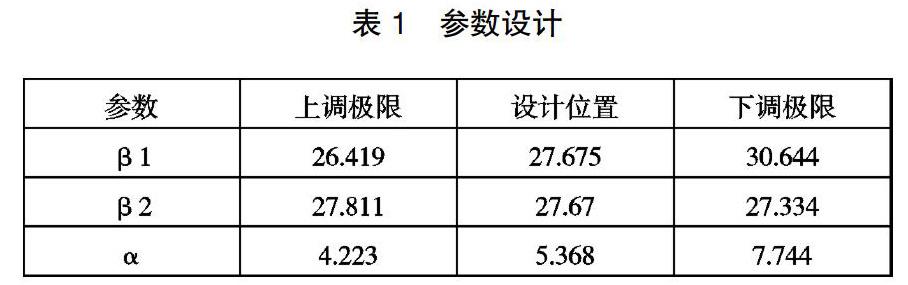
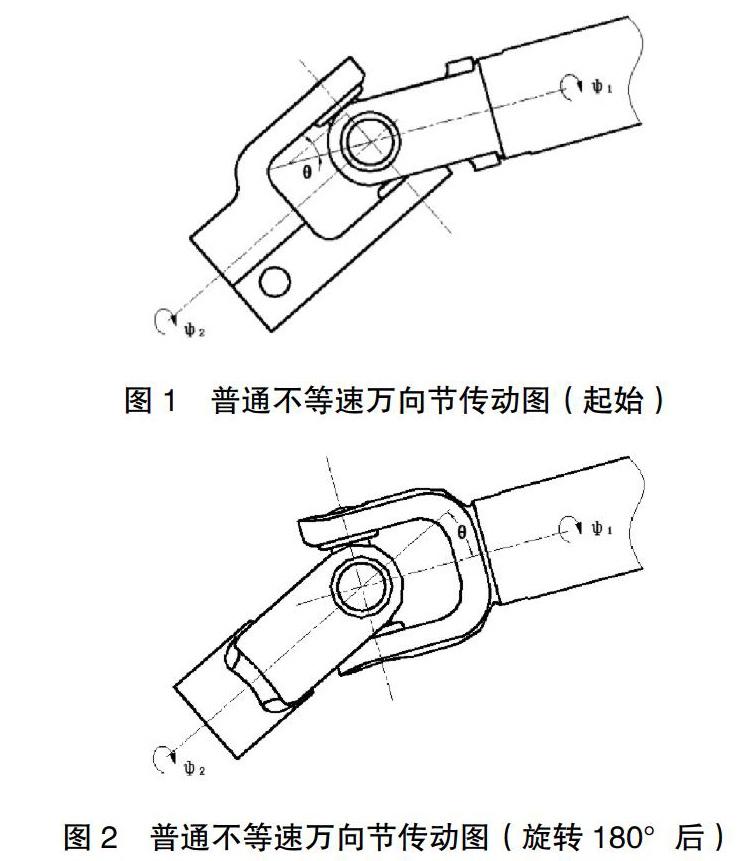
不等速万向节传动时，在图1处起始时，输入端转速大于输出端，其中有：

但当转动180°之后，见图2，输入端转速则小于输出端，其中有：

1.3 空间双万向节不等速传动计算式

通过单万向节的不等速传动，可以推出空间双万向节的不等速传动计算式，并且三段式传动轴可以等效为两段式传动形式，则力矩波动可以简化为如下公示：

α——输入轴和中间轴所在平面与中间轴和输出轴所在平面的夹角;

ψ——中间轴下端连接叉的相位角;

βe——等效夹角;

2 基于MATLAB的数值计算

2.1 概述

MATLAB是美国MathWorks公司发布的商业用途的数学软件，主要应用于算法、数据可视化、数据分析计算的高级技术计算语言和交互式环境。MATLAB的基本数据单位是矩阵，它的指令表达式与数学、工程中常用的形式十分相似。

MATLAB软件功能强大，人机交互界面友好。在本文所述中，主要是应用其处理数值、图像处理技术，以便从枯燥的、杂乱无章的数字中寻求解决方法。

2.2 计算平台的建立思路

为了建立与整车布置环境相同的计算平台，必要的两个条件是：转向系统相关零部件的硬点布置数据和人机调节的相关的技术参数。

3 力矩波动计算平台的步骤和验证

3.1 建立总布置模型

3.1.1 设计参数定义

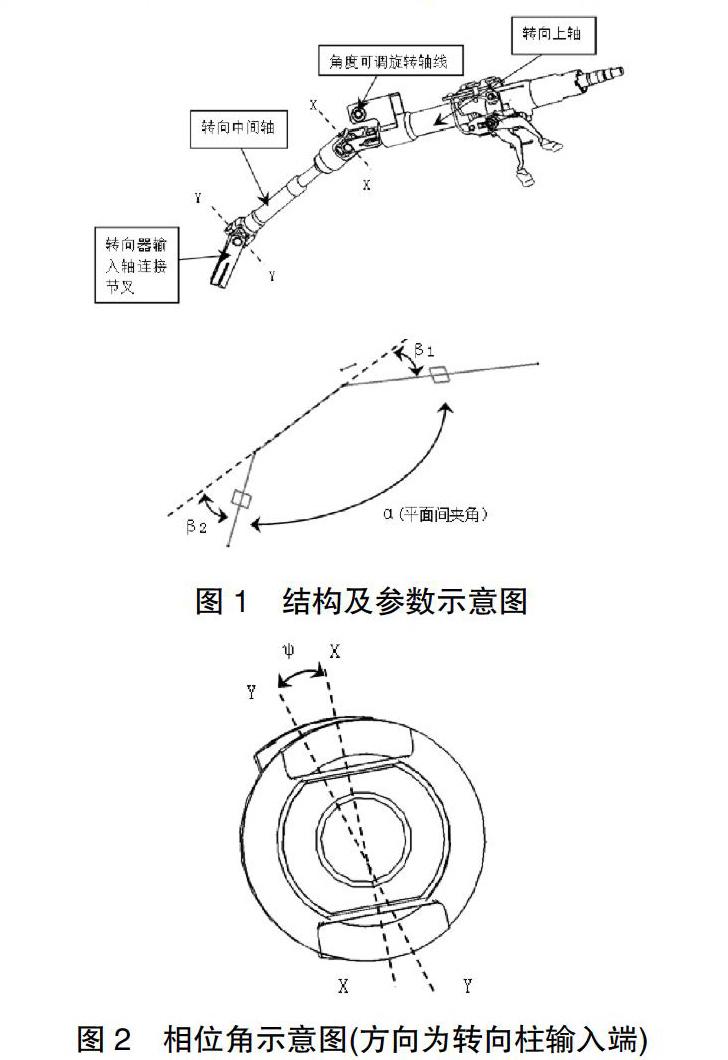
两段式转向柱结构见图1，相位角定义见图2。

其中：相关参数说明如下：

β1——输入轴与中间轴夹角（单位：°）

β2——中间轴与输出轴夹角（单位：°）

α——输入轴和中间轴所在平面与中间轴和输出轴所在平面的夹角（单位：°）

ψ——相位角（单位：°）

3.1.2 设计参数输入

例：以某款车型的转向柱总成角度可调设计为-2.8°～+1.2°，相关的设计参数见表1：

3.1.4 相位角取值范围粗定义

考虑到转向中间轴总成的节叉装配工艺，相位角的公差一般定义为±2°，因此相位角范围在-（4.2-2） °～-（7.8+2） °之内较理想，圆整后分别把相位角设定为ψ=-2.2°、-3.2°、-4.2°、-5.4°、-6.2°、-7.2°、-8.8°、-9.8°。

3.1.5 力矩波动计算

把上述参数代入到力矩波动计算公式（其中，按表1分别代入上调极限、设计位置、下调极限的参数于下式中计算）可以得到在各取值状态下力矩波动图情况分别见图3～图10。其中：每张曲线图含上调极限、设计位置、下调极限的三条曲线。红色线为上调极限下的力矩波动曲线、蓝色线为设计位置下的力矩波动曲线、黑色线为下调极限下的力矩波动曲线

3.1.6 相位角的确定

综合评估后，取ψ为-5.4°时，在角度可调全行程范围下力矩波动较理想。此时，上调极限为±1.2%≤±5%，下调极限为±3.2%≤±5%，设计位置为±0.1%≤±2%，符合设计要求。

4 结束语

本文通过基于MATLAB的数值计算软件平台来建立整车转向系统的四向调节力矩波动计算模型，来达到模拟整车环境的目的，并且为后续量产设计方案提供一种新的思路和方法，特别是在新车型的研发过程中，可以起到关键作用。

参考文献

[1] 张洪欣.汽车设计（第二版）[M].北京：机械工业出版社，1989.

[2] 冯振东.空间多万向节传动的转角差和当量夹角的计算[J].长春：吉林工业大学学报，1982.

[3] 刘惟信.汽车设计[M].北京：清華大学出版社，2001.

[4] 刘大勇.某车型转向系统匹配工作[J].实用汽车技术，2006，（3）：24- 25.

[5] 王沫然.MATLAB 6.0与科学计算[M].北京：电子工业出版社，2001.

[6] 郑继明，朱伟，刘勇等.数值分析[M].北京：清华大学出版社，2016.