一种低损耗的对称双楔形太赫兹混合表面等离子体波导*

王芳 张龙 马涛† 王旭 刘玉芳 马春旺

1) (河南师范大学电子与电气工程学院, 新乡 453007)

2) (河南省光电传感集成应用重点实验室, 新乡 453007)

3) (河南师范大学物理学院, 新乡 453007)

本文研究了一种适用于太赫兹频段的对称双楔形混合等离子体波导.采用有限元法对其混合模式特征进行数值模拟, 阐述了波导的传播长度、归一化有效模场面积和品质因子等特性随波导几何参数的变化规律.结果表明, 对称双楔形混合等离子体波导在太赫兹频段可获得良好的模场约束能力和低损耗特性, 在有效模场面积达到l2/10280时, 传播长度达到51 × 103 µm.波导参数最优时的平行对称楔形波导在忽略波导间串扰时, 波导间距小于16 µm时的耦合长度约为8958 µm.通过对比发现, 相比于先前的对称微楔形波导结构和对称蝴蝶结波导结构, 对称双楔形混合等离子体波导在传输特性和耦合特性方面都具有更大的优势, 将在光学力捕获、生物分子传输以及高密度集成电路设计等方面具有潜在的应用前景.

1 引 言

表面等离子体学是纳米光电子领域非常重要的研究方向, 表面等离子体激元 (surface plasmonpolaritons, SPPs)因其亚波长尺寸传输和局域场增强效应的优点已成为研究的热点[1−3].表面等离子体波导具有能够突破衍射极限、整体尺寸较小且制作方便等优势, 因此备受研究者的关注[4],可广泛应用于耦合器[5]、偏振转换器[6]、M-Z干涉结构[7,8]、光开关[9]、纳米天线[10,11]以及折射率传感器[12]等光子和光电器件的设计.为了提高SPPs波的传输距离, 可以用介质波导替代SPPs波导(即减小SPPs波导的长度)来实现低损耗传输[13].在介质芯层中增加金属薄层[14]、利用混合SPPs波导[15]和双层介质加载SPPs波导[16]等方法也可以增加SPPs波的传输距离.近年来, 混合表面等离子体波导 (hybrid plasmonicwaveguides, HPWs)以其独特的突破衍射极限和在亚波长尺度下提供紧密光约束的能力, 被认为是大规模光子集成器件最有前途的候选者之一[4].目前, HPWs波导有圆柱形[2]、楔形[17]、领结形[18]及蝴蝶结 (bow-tie,BT)[19]等多种形状.HPWs波导的设计不仅降低光在其中的传播损耗, 还进一步提高对光场的限制能力, 在超高密度光子集成器件和高灵敏度传感等领域具有很大的潜在应用.

太赫兹(terahertz, THz)波具有许多优异特性, 比如: 能量需求低、穿透衰减小、信噪比高、对生物大分子拥有强吸收和谐振特性等[20].与其他波段的电磁波相比, THz波具有直接探测生物分子信息的能力, 它在药品生产的监控、生物大分子的光谱识别[21]等方面具有巨大的应用潜力.目前, 对支持混合等离子体模式的混合等离子体太赫兹波导 (hybrid plasmonic terahertz waveguide,HPTWG)的研究具有良好的应用前景.由于THz波的频率占据微波和红外之间, HPTWG可以实现低损耗微米级传播及较高的模场限制[22].虽然长程太赫兹混合等离子体(long-rang hybrid THz SPPs, LR-HTSPPs)波导减少了传播损耗,实现了厘米级的传播长度, 但其束缚能力较弱[23].

为了更好地权衡模式束缚和传播长度之间的相互关系, 本文研究了一种对称双楔形太赫兹混合表面等离子体波导 (wedge-to-wedge THz hybrid SPPs waveguide, WWTHSW)结构.利用有限元方 法 (finite element method, FEM)研 究 了WWTHSW的模式特性和传输特性及其随波导结构尺寸变化的规律, 并分析了两条平行WWTHSW间的耦合特性.最后, 我们对比了WWTHSW与对称微楔形太赫兹混合等离子体(hybrid THz microwedgeSPPs, HTMWSPPs)波导和对称型蝴蝶结太赫兹混合等离子体(hybrid THz bow-tie SPPs, HTBTSPPs)波导的性能.

2 模型及数值模拟

WWTHSW的三维结构示意图和截面图如图1(a)和图1(b)所示, 由两个对称放置的完全相同的硅楔形波导 (silicon wedge waveguides, SWWs)和夹在中间的Ag层构成, 两者间隔为g.波导的包层材料选用氮化硅(Si3N4).SWWs的高度为H,楔形尖端采用圆角化处理, 曲率半径为r, 圆角为a.Ag 层的厚度为 d = 100 nm, 楔形尖端曲率半径也为 r, 圆角为 θ.曲率半径设定为 r = 2 µm.Si,Si3N4折射率分别为3.455和2.根据Drude模型[24,25],Ag的介电常数可表示为

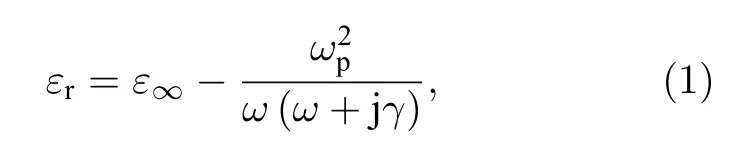
其中, e∞为高频介电常数, w 为入射光角频率, g 为阻尼项, wp为等离子体角频率.

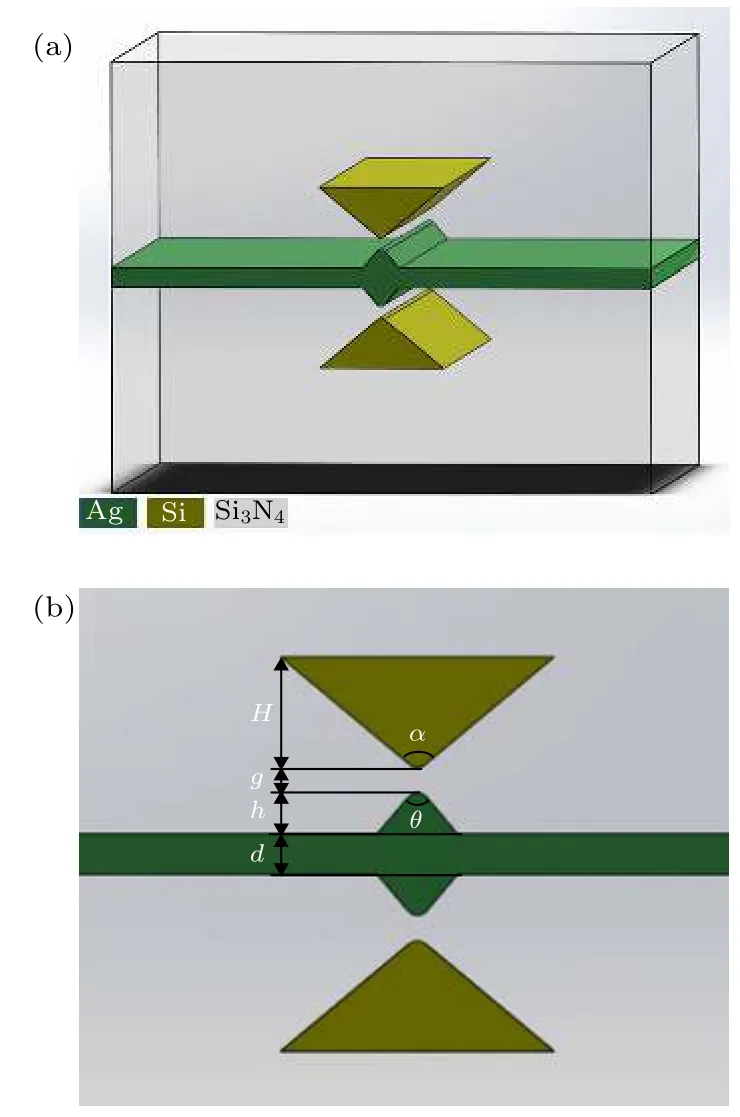
图1 WWTHSW 示意图 (a) 三维图; (b)截面图Fig.1.Schematic diagram of the proposed WWTHSW:(a) 3D diagram; (b) cross-section.

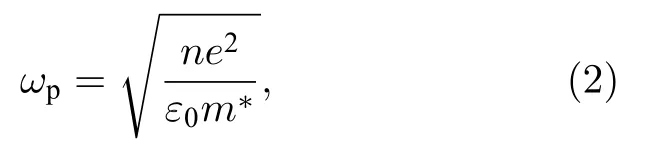
其中, m*, e和n分别为电子有效质量、电子电荷和载流子密度; e0为空间的介电常数.参数 wp=1.37 × 106rad/s, g = 8.20 × 1013rad/s[24].

为了定量分析HPTWG的模式和传输特性,通常用有效折射率(neff)、传播长度(Lp)、归一化模场面积[17](A)、品质因数[26](figure of merit, FOM)以 及 模 式 分 布 特 性[2](the mode character,MC)等参数衡量其特性.

传播长度Lp为

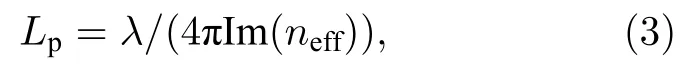
其中, l是真空中的波长, Im(neff)是模式有效折射率的虚部.

A 定义为 Am/A0.其中: A0= l2/4 表示自由空间中的衍射限制面积; Am为有效模场面积, 反映波导对模式的束缚能力, 定义为

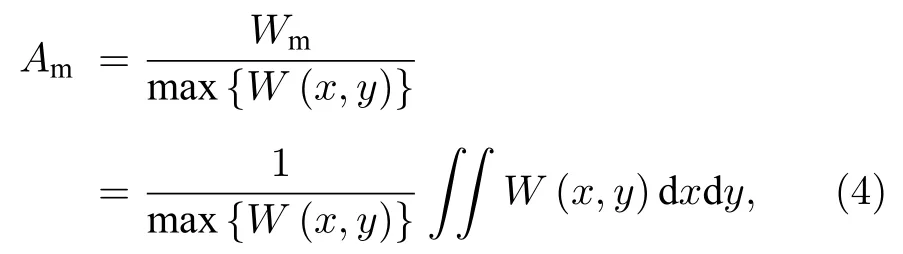
其中, Wm是模式的总能量, W(x, y)是能量密度.

为综合衡量波导的传输特性, 定义品质因数为

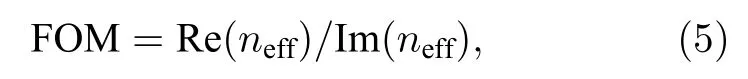
其中, Re(neff)是模式有效折射率的实部.

为描述混合等离子体波导模式中SPPs模式和波导模式之间的差异, 引入模式特性(MC):

本文采用FEM对太赫兹频段的模式特性和传播特性进行研究.使用商用ComsolMultiphysics软件中的波动光学模块, 模型采用散射边界条件,仿真时的模型外层区域宽度均设置为2l, 应用非均匀三角网格进行剖分并设置最小单元网格大小为 d/2, 由于 Ag 层内几乎没有场分布, 因此, d/2能够保证模型计算的收敛性的精度.

3 波导模式特性及参数优化

为了优化WWTHSW的性能, 利用Comsol Multiphysics软件中的模式分析研究不同波导几何参数下波导中存在的HPTWG的模式特性.以下仿真中, 入射光的频率设置为 1 THz.楔形波导的高度H与间隙g对MC的影响如图2(a)所示,当 H 小 于 40 µm 时, MC < 0.5, 波 导 模 式 以SPPs模式为主; 当 H 大于 40 µm 时, MC > 0.5,波导模式以SWWs模式为主.图2(d)—(f)所示,H = 10 µm 时, 能量主要集中在间隙中 Ag 与Si3N4的交界面附近; 当 H = 40 µm 时, 能量依然主要集中在间隙中, 然而有部分能量向Si基楔形波导转移; 当 H = 90 µm 时, 模场的能量主要分布在Si基楔形波导内部.为了优化设计参数, 我们研究了波导的H和g对混合对称双楔形波导Lp和A的影响, 如图2(b)和(c)所示.WWTHSW的其他参数设定为: h = 2 µm, q = 80°, a = 100°和d = 100 nm.从图2(b)可以看出, 对于同一 g, 随着H的增加, Lp呈上升趋势.当H小于40 µm时,波导模式以SPPs模式为主, H的增大使得模场能量逐渐远离金属表面, 降低波导内的欧姆损耗, 从而使 Lp迅速增加[27].当 H 大于 40 µm 时, 模式能量开始向Si基楔形波导转移, 模式以SWWs为主, Ag 引起的欧姆损耗减小, 使 Lp有所增加.从图2(b)内局部放大图可以看出, 当H小于37 µm时, Lp随 g的增大而减小, 但变化较小; 当 H 大于37 µm 时, Lp随 g 的增大而增大.在 H 等于 37 µm时, 不同 g 下的传播长度均为 42.5 × 103µm.之后随H的增大Lp逐渐增大; 当H达到90 µm时,Lp从 47.7 × 103µm 增大至 61.1 × 103µm.

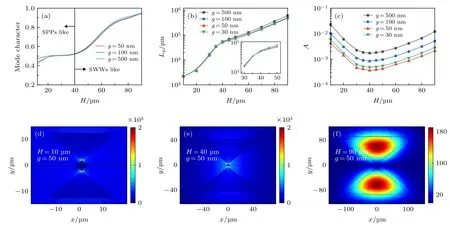
图2 不同 H 和 g 时, WWTHSW 的模式分析 (a) MC, (b) Lp, (c) A; 模场分布: (d) [H, g]= [10, 0.05]µm, (e) [H, g]= [40, 0.05]µm,(f) [H, g]= [90, 0.05]µmFig.2.Modes analysis of the WWTHSW with different H and g: (a) MC, (b) Lp, and (c) A;and normalized EM energy density distributions: (d) [H, g]= [10, 0.05]µm; (e) [H, g]= [40, 0.05]µm; (f) [H, g]= [90, 0.05]µm.

从图2(c)可以看出, 对于相同的 g, A随着H的增加而先减小再增大, H约40 µm处A达到最小值.对于较小的 SWWs(H 小于 40 µm), 混合模式主要由 SPPs模式决定 (MC < 0.5), 观察归一化能量密度分布图2(d)可发现, 该模式约束相对较弱.当楔形波导的尺寸增大时(H大于40 µm),WWTHSW模式表现为低损耗SWWs模式(MC> 0.5), 大多数模式能量主要集中在高介电常数的SWWs芯部(如图2(f)), 从而导致模式面积增大.在 H = 40 µm 时 (MC = 0.5), 波导模式介于 SWWs和SPPs模式之间, 处于一种临界状态, 同时具有SWWs和SPPs的模式特性, 此时模式面积A有最小值.当H不变, A随着 g的增大而增大, 这是由于g的增大使得模式能量分布逐渐远离Ag表面, 波导模式能量更加分散, A随之增大, 变化范围从 3.62 × 10–4到 3.69 × 10–3.因此, 本文以下的研究中, 选择 H = 40 µm, g = 50 nm, 此时, Lp为 51.5 × 103µm, A 为 3.62 × 10–4.与文献 [23]提出的LR-HTSPPs波导相比, Lp增大将近3倍,而A减小1个数量级.

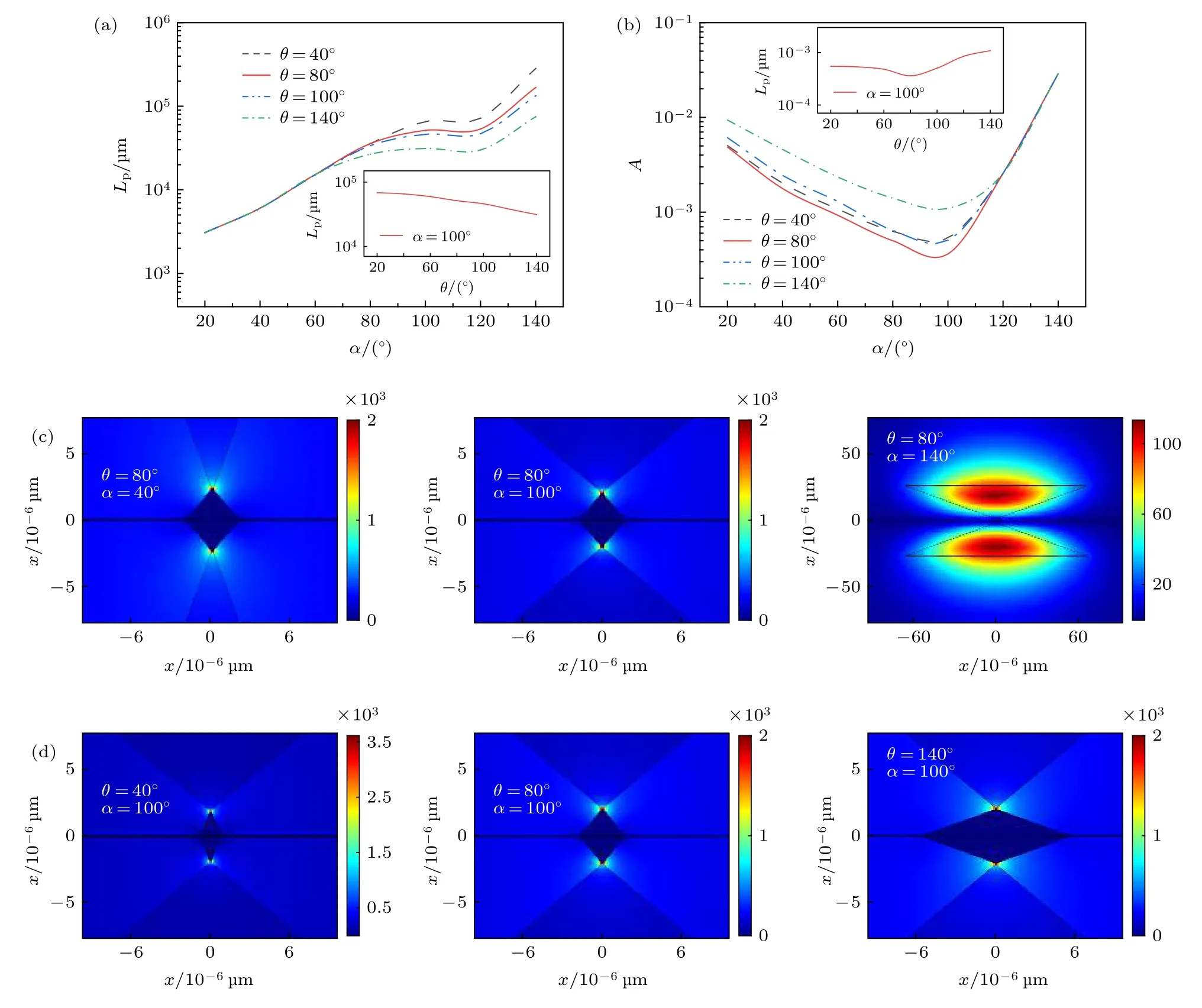
图3 不同 a 和 q 时, WWTHSW 的模式分析 (a) Lp, (b) A; (c)模场分布随 a 的变化 (q = 80°); (d) 模场分布随 q 的变化 (a = 100°)Fig.3.Modes analysis of the WWTHSW with different a and q, (a) Lp, (b) A; and normalized EM energy density distributions:(c) with different a at a fixed q of 80°, (d) with different q at a fixed a of 100°.

SWWs的a和q也是影响WWTHSW模式性能的重要几何参数.传播长度Lp随a和q变化的规律如图3(a)所示, 对于任意q, Lp随着a的增大而增大.当 a < 70°时, q 的变化对 Lp几乎没有影响; 而当 a > 70°时, Lp随着 q 的增大而减小.A随a和q的变化关系如图3(b)所示, 对于任意q, A 随着 a 的增大先减小再增加, 在 a = 100°附近存在最小值.如图3(b)的插图所示, 当 a =100°时, A也随着 q的增大先减小再增加.图3(c)给出在 q = 80°时, 不同 a 的 WWTHSW 的归一化能量密度分布图.当 a = 40°和 100°时, 波导模式以SPPs模式为主, 电磁场能量主要集中在Si楔形角与Ag楔形角之间, a增大, 模场能量逐渐远离金属表面, 欧姆损耗减小, 从而使Lp增大;此时, 模式能量更加集中, A 反而减小.当 a =140°时, 模式以 SWWs为主, 模式能量主要集中在 SWWs内, 导致欧姆损耗减小, Lp增大, 模场能量无法限制在交界面, 从而使A也增大.图3(d)给出在 a = 100°时, 不同 q 的 WWTHSW 的归一化能量密度分布图.此时, 波导模式以SPPs模式为主, 随着 q 从 40°增加到 80°再到 140°, 模场能量与金属楔形的接触面积不断扩大, Ag引入的欧姆损耗增加, Lp减小.当 q = 80°时, 模场能量更集中于双楔形之间, A 达到最小值 3.62 × 10–4, 此时传播长度为 5.14 × 104µm.在本文以下研究中, 选用参数 q = 80°, a = 100°.

图4(a)和(b)给出WWTHSW的Lp和A随着d和h的变化规律.由图4可知, Lp和A随着d 的增加而略微减小.当 d 不变, h = 0 时, Lp和A 比 h = 2 µm 和 5 µm 时大.结果表明, 增加Ag 楔形结构 (h = 2 µm 和 5 µm)后的波导相比于没有增加Ag楔形结构(h = 0)时的Lp略有减小, 但却具有更好的模场限制能力.从图4(c)中的归一化能量密度分布可以看出, 当h为2 µm和5 µm时, 光场全部被限制在超深亚波长区域内, 从而减小了有效模场面积; 而在 h = 2 µm 和 h = 5 µm时的微米边缘的模式轮廓差几乎可以忽略不计.对于 h = 2 µm, WWTHSW 的横向模式宽度 W =0.01 µm(W, 其定义为能量密度衰减到其峰值的1/e的全宽度[17]), 相比于 h = 0 时横向波导模式的 W = 1.2 µm, 减小 12 倍.本文以下的研究中,选用 d = 100 nm, h = 2 µm.

4 不同对称性SPPs波导比较

图4 不同 d 和 h 时, WWTHSW 的模式分析 (a) Lp、(b) A; (c) 沿 x 方向的归一化能量密度Fig.4.Modes analysis of the WWTHSW with different d and h, (a) Lp, (b) A, and (c) normalized EM energy density.

为了比较不同对称性混合表面等离子体波导结构的特性, 利用FEM对WWTHSW、HTMWSPPs波导和HTBTSPPs波导的模式特性和传输特性进行了分析.HTMWSPPs波导、HTBTSPPs波导的截面模型如图5(a)所示.

图5(b)为Lp与A的相关性对比图.在仿真中WWTHSW和HTMWSPPs波导选择最佳参数 H = 40 µm, h = 2 µm, q = 80°, a = 100°, g =50 nm, d = 100 nm.HTBTSPPs 波导选择最佳参数 H = 10 µm, W = L = 30 µm.由图5(b)可知,WWTHSW比HTMWSPPs波导和HTBTSPPs波导的 Lp更长.相比于 HTMWSPPs波导,WWTHSW由于尖端场增强效应, 光场主要聚集在楔形波导的顶点附近[1], 具有更强的模场限制能力; 而相比于 HTBTSPPs波导, WWTHSW 没有矩形Si波导部分, 有利于模场能量的集中, 因此具有更小的模场面积.g 在 50 nm 到 2 µm 范围内,WWTHSW的有效模场面积(Am= l2/10280)相比于 HTBTSPPs波导 (Am= l2/5405)减小近2 倍, 相比于 HTMWSPPs波导 (Am= l2/7407)减小近 1.5倍.在相同的有效模场面积 Am=l2/5405 的情况下, WWTHSW 的Lp为65×103µm,是 HTMWSPPs波 导 (Lp= 54 × 103µm)的1.2 倍, 是 HTBTSPPs波导 (Lp= 33 × 103µm)的 2 倍.而在相同的传播长度 Lp= 51 × 103µm的情况下, WWTHSW的有效模场面积 (Am=l2/10280), 比 HTBTSPPs波导 (Am= l2/4422)减小 2 倍.由图5(c)可知, 相比于 HTBTSPPs波导、HTMWSPPs波导, WWTHSW品质因数更好.因 此 , WWTHSW 相 比 HTBTSPPs波 导 、HTMWSPPs波导在相似的传播长度下, 具有更强的模场限制能力和更好的品质因数.

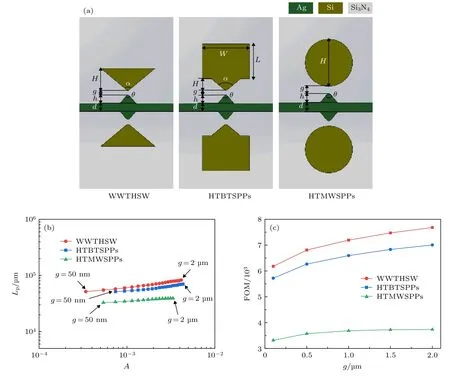
图5 不 同 波 导 性 能 比 较 (a) WWTHSW, HTMWSPPs 和 HTBTSPPs波 导 的 截 面 图 ; (b) WWTHSW, HTMWSPPs 和HTBTSPPs波导的A与Lp关系图; (c)品质因数Fig.5.Performance comparison of the WWTHSW, HTMWSPPs and HTBTSPPs wavguide: (a) cross-section views; (b) the relationship between A and Lp; and (c) FOM with different parameters.

为了分析WWTHSW的耦合特性, 构建两根间距为D的平行WWTHSW, 如图6(a)所示.通常, 波导的耦合特性由波导的耦合长度 Lc= π/(bs–ba)来衡量, 其中bs和ba分别是两个相邻波导的对称和反对称模的传播常数[28].

WWTHSW、HTBTSPPs和 HTMWSPPs波导的Lc随两条平行波导中心间距D的对应关系如图6(b)所示.在仿真中, 采用上述最佳参数, H =40 µm, h = 2 µm, q = 80°, a = 100°, g = 50 nm,d = 100 nm.图6(a)为 WWTHSW 在 D = 12 µm参数下的对称和反对称模式的归一化能量密度分布.从图 (6)中可以看出, WWTHSW 的 Lc高于HTBTSPPs波导、HTMWSPPs波导的 Lc, 这种差异随着间隔 D 增大变化更加明显.当 D = 12 µm时 , HTMWSPPs波 导 的 Lc为 2195 µm, 而WWTHSW的 Lc为 2749 µm, 是 HTMWSPPs波导的 1.2 倍.当 D = 20 µm 时, HTMWSPPs波导的 Lc为 20361 µm, WWTHSW 的 Lc为 28896 µm,是 HTMWSPPs波导的 1.5倍.该结果表明, 在相同的 Lc下, 与 HTBTSPPs波导和 HTMWSPPs波导相比, 本文提出的WWTHSW可显著降低串扰, 这对于高度集成的光子器件来说是一个极大的优势.

另外, 波导耦合过程中的传播损耗是不可避免的, 因此, 用最大功率传递[29](Pmax)表明波导损耗特性,

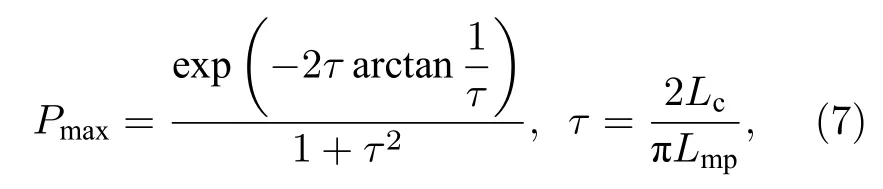
其中, Lmp为对称和反对称模式的平均衰减长度,

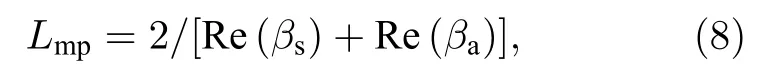
其中, Re(bs)和Re(ba)分别是bs和ba的实部.

图6(b)为WWTHSW、HTMWSPPs波导和HTBTSPPs波导的Pmax与间距D的关系图.从图6(b)可以看出, 对于相同的最大功率传输Pmax,两个HTWWSPP波导之间的间隔距离D小于两个HTBTSPPs波导和HTMWSPPs波导之间的间隔距离 D.忽略波导间串扰 (Pmax< 10–3)[29]时, WWTHSW 最 小 间 隔 距 离 D 为 15.8 µm,HTBTSPPs波导最小间隔距离 D为 17.3 µm,HTMWSPPs波导最小间隔距离 D为 18.6 µm;WWTHSW最小间隔距离相比于HTBTSPPs波导最小间隔距离减小1.5 µm, 相比于HTMWSPPs波导最小间隔距离减小2.8 µm.结果表明WWTHSW能够实现更高的封装密度.

图6 波导耦合特性分析 (a)平行波导三维结构示意图; (b)耦合长度随D的变化; (c)最大传输功率随D的变化Fig.6.Coupling characteristic of waveguides: (a) schematic diagram parallel waveguides; (b) Lc versus the separation between the two waveguides; (c) the maximum transfer power (Pmax) as a function of distance D.

5 结 论

本文研究了一种可实现低损耗传输的对称双楔形太赫兹混合表面等离子体波导.利用数值模拟对其支持的表面等离子体模式的传输特性和场分布特性进行研究发现, Ag层的厚度d、双楔形介质波导间隙g及楔形波导几何参数q、a、H都会对WWTHSW的模式特性产生影响.在最佳参数H =40 µm, h = 2 µm, q = 80°, a = 100°, g = 50 nm,d = 100 nm 的条件下, 当 Am达到 l2/10280 时,Lp接近 5.1 × 104µm.相比于其他已经提出的混合等离子体波导结构, WWTHSW的归一化模式面积减少一个数量级, Lp增加约3倍.WWTHSW能够在太赫兹频率实现低损耗传播和超深亚波长模式限制.通过对WWTHSW的耦合特性进行分析可知, 在忽略波导间串扰时, 波导间距小于 16 µm时的耦合长度约为8958 µm, 相比于HTMWSPPs波导、HTBTSPPs波导结构, 具有串扰低、封装密度高的优势.因此, WWTHSW的研究对深度亚波长尺寸下光子和太赫兹器件的高密度集成具有重要意义, 为微米光子器件和太赫兹器件的设计提供一种可行的波导结构.