模糊三支形式概念分析与概念认知学习

徐伟华 杨蕾 张晓燕

摘要：目前，三支形式概念分析只适用于传统的形式背景，无法处理模糊环境中的形式背景。为了解决这个问题，文中结合三支形式概念分析与模糊集理论，提出了模糊三支算子及其逆算子，并对其相关重要性质进行了研究。在此基础上，定义了两类模糊三支概念，即属性导出模糊三支概念和对象导出模糊三支概念。随后，以对象导出的模糊三支概念为例，讨论了模糊三支概念的概念认知学习方法，实现了不完备模糊三支概念的认知学习。最后，为了更好地解释和理解所提出的理论，文中进行了案例分析并设计了认知学习算法，通过数值实验验证了所提出方法的有效性，进一步丰富了三支形式概念分析和概念认知学习理论。

关键词：模糊三支概念；模糊三支算子；形式概念分析；概念认知学习

中图分类号：O235；TP18

DOI：10.16152/j.cnki.xdxbzr.2020-04-002开放科学（资源服务）标识码（OSID）：

Fuzzy three-way formal concept analysisand concept-cognitive learning

XU Weihua1， YANG Lei2， ZHANG Xiaoyan1

（1.College of Artificial Intelligence， Southwest University， Chongqing 400715，  China;

2.School of Science， Chongqing University of Technology， Chongqing 400054， China）

Abstract： At present， the three-way formal concept analysis is only applicable to the traditional formal context， and can′t deal with the formal context in the fuzzy environment. In order to solve this problem， this paper combines the three-way formal concept analysis with the theory of fuzzy set， proposes the fuzzy three-way operator and its inverse operator， and studies its related important properties. On this basis， two kinds of fuzzy three-way concepts are defined， namely attribute-induced fuzzy three-way concepts and object-induced fuzzy three-way concepts. Then， taking the object-induced fuzzy three-way concept as an example， the concept-cognitive-learning approach to the fuzzy three-way concept is discussed， and the cognitive learning of the incomplete fuzzy three-way concept is realized in the environment. Finally， in order to explain and illustrate precisely the proposed theory， the paper gives a case study and designs an algorithm， at the same time， it uses some data sets for experimental evaluation. These results further enrich the theory of three-way formal concept analysis and concept-cognitive learning.

Key words： fuzzy three-way concept; fuzzy three-way operator; formal concept analysis; concept-cognitive learning

概念一词来源于哲学，是外延与内涵的统一。概念一般被认为由外延和内涵构成，其中概念的外延是指这个概念所覆盖的对象范围，即该概念所覆盖的特征所反映的对象，而概念的内涵是指这个概念具体涵义，即该概念所覆盖的对象指向的特征。随着科学技术的发展，尤其是大数据科学和人工智能的兴起，概念认知学习理论（concept-cognitive learning，下文簡称CCL）逐渐成为了认知科学、脑科学、计算机科学等领域的研究热点。狭义来说，CCL可以看为形式概念分析与认知计算相结合的一个新的研究方向。CCL的主要思想是指通过具体的认知模型从给定线索中进行概念学习，以揭示人脑概念学习的系统性规律。早在2007年，张和徐［1］提出了基于粒计算的概念认知模型，且实验表明该模型是可行的［2-3］。这一研究逐步引起了同行专家的广泛关注，并取得了非常好的研究成果［2，4-26］。

众所周知，形式概念分析［27］是Wille于1982年提出的，为我们从形式背景中获得认知概念提供了有效的数学基础。概念格作为形式概念分析的核心工具，又称概念格理论，简称概念格。到目前为止，对概念格的研究已经取得了很大的成果，如概念格的构造［28-29］、概念格的属性约简［30-33］以及概念格与模糊集［34-36］、粗糙集［37］，粒度计算［38-40］，认知计算［3，6］等的组合。然而，过高的概念格构建成本，导致概念认知学习效率低下。粒计算方法［6］可以有效地解决这一问题。从信息粒化的角度出发，徐等［2］

研究了从任意信息粒向充分、必要、充要信息粒的转化方法，实现了概念的认知学习。徐和李［3］在模糊数据集中提出了概念的双向学习方法。

另外，加拿大学者姚［24］于2009年提出了三支决策的概念。近年来，形式概念分析与三支决策的交叉研究受到了学者们的广泛关注。姚［41］研究了不完备形式背景下的三支形式概念分析方法。任和魏［42］讨论了三支概念格的属性约简。李等人［43］利用辨别矩阵在不完备背景下寻找约简集，简化了三支概念格的知识单元。这些构造方法实现了形式概念分析中的三支决策，统称为三支概念分析。除了三支概念分析，概念格和三支决策，还有另一种组合模式，即三支概念学习［7］。与三支概念分析的结构化法不同，三支概念学习主要是通过公理化的方法将三支决策思想融入到概念学习中。李等［7］从认知的角度研究了多粒度三支概念学习方法。此外，由于三支概念学习往往涉及到多源数据环境，黄等［25］在多源数据环境下研究了三支概念学习的加权信息融合方法。石等［23］提出了一种基于决策背景的CCL模型，在动态环境下实现了概念的增量学习。

在实际应用过程中，除了传统的形式背景还存在许多的模糊形式背景。另外，在模糊环境中学习三支概念是一个非常有意义的研究课题。受此启发，本文提出了模糊三支形式概念分析方法，研究了模糊三支概念的认知学习问题。

1 预备知识

本节对形式概念分析的基本概念，如三支形式概念分析和模糊形式概念进行了简要的回顾。更详细的描述可以在文献［27，44-46］中找到。

形式概念分析是由Wille提出的一种从形式背景中进行数据分析和规则提取的有用的工具。一个形如（U，A，I）的数据表被称作一个形式背景，其中U是对象集，A是属性集，I是U和A之间的二元关系。在一个（U，A，I）中，x∈U，a∈A，（x，a）∈I说明x拥有a或者a被x拥有。（x，a）I说明x没有a或者a不被x拥有。为了简便，通常分别使用“I（x，a）=1”和“I（x，a）=0”表示（x，a）∈I和（x，a）I。

4 案例分析和数值实验

为了更好地说明上节中提出的三支概念的认知学习方法，我们在本节中通过一个案例来说明本文提出的理论。同时，设计对象导出模糊三支概念的学习算法，并通过8个模糊数据集对算法进行了分析。

4.1 案例分析

能够反映发展中国家偿债能力的指标因素有很多，例如，地区生产总值，人类发展指数，收讫货物等。在本案例中，选择了7个指标对10个发展中国家的偿债能力进行评估。表1所示是一个模糊形式背景（U，A，），其中U=｛Algeria;Bhutan;Colombia;Dominica;Grenada;Jamaica;Lesotho; Mexico; Nigeria; Rwanda｝，U中每一個元素被记为xi（i=1，…，10）表示一个发展中国家;A=｛GRP，UR，EGI，HDI，DE，GS，FCR｝评价指标的集合。

现在，为了鼓励发展中国家更好地发展，联合国决定向综合国力领先的发展中国家提供贷款。首先，必须考虑这些国家的偿还能力。本文提出的学习方法能很好地解决这一问题。经过初步评估，本文得到了一个模糊三支对（，（，）），其中是综合国力领先的发展中国家。因为综合国力领先是一个模糊的概念，所以是一个模糊集。（，）是属性集A的模糊序对。最后，应该选择所有满足模糊属性且不满足模糊属性的发展中国家。然而，最初得到的可能包含不满足属性或满足属性的对象，因此需要学习模糊三支对（，（，））。在这里，人为设定，，为

4.2 实验评估

为了证明第3节所提理论的有效性和可行性。结合相关理论分析，设计了一个模糊三支概念的学习算法，如算法1所示。算法1达到了从普通模糊三支对中获取模糊三支概念的目的。

在进行实验之前，需要得到实验所需的模糊数据集和初始模糊三支对。接下来，我们将介绍模糊数据集和初始模糊三对的获取方法。

初始模糊三支对（，（，））的生成：对于任意的（U，A，），随机选择|U|*α个对象作为中的对象并为中每一个对象赋予隶属度，阈值α控制中的对象占所有对象的比例。类似地，和可以通过随机赋予A中属性隶属度的方式获得。需要注意的是：和中任意属性的隶属度

实验数据的来源：为了获得实验数据，我们从机器学习数据库（https：∥archive.ics.uci.ed u／ml／index.php）中下载了4个数据集，即“Movement-libras”，“Vehicle”，“Winequality-red”和“Winequality-white”。并进行相应的模糊处理，即数据集中每一列的数据除以该列的最大值。此外，利用Matlab生成了4个模糊数据集，即“owndata1”，“owndata2”，“owndata3”和“owndata4”。有关数据集的更多信息，请参阅表2。整个实验是在个人电脑上进行的。实验环境详见表3。

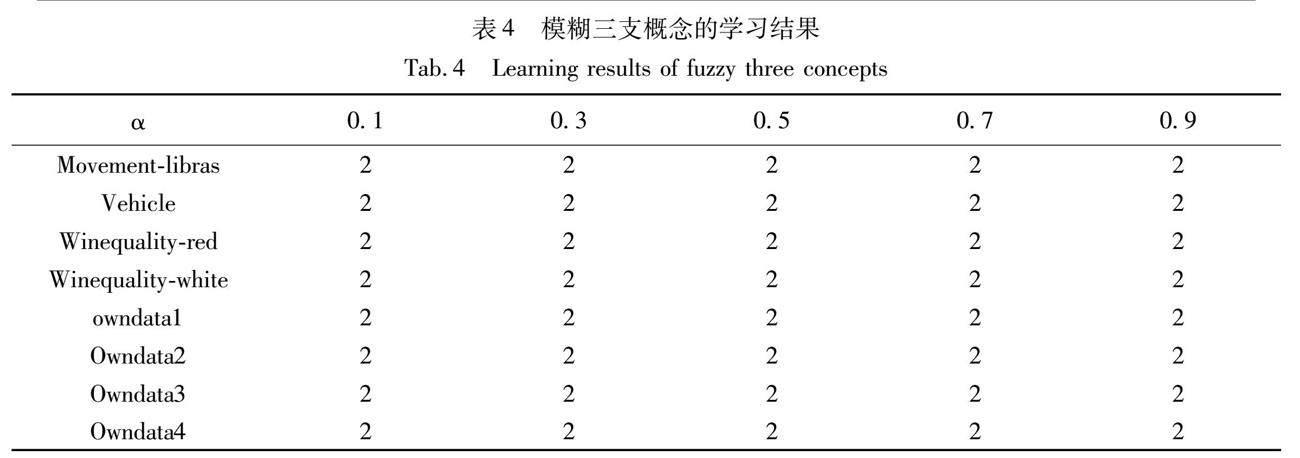
为了测试算法1中模糊三支概念的获取能力，本文进行了相关的实验。通过设置α值得到初始模糊三对。在本实验中，将每个数据集下的α值设为0.1，0.3，0.5，0.7和0.9。实验过程中记录了在每次实验得到的模糊三支概念的数目和每次实验的运行时间。实验结果见表4～5。

表4记录了在每个数据集中一个模糊三支对通过概念学习获得的模糊三支概念的数量。表5记录了每次实验的运行时间。从表4～5，可以得出以下结论。

1）在每个数据集中，每次实验的运行时间与初始模糊三支对选择的对象数量和属性数量密切相关。随着初始模糊三支对中包含的对象和属性数量的增加，运行时间也随之增加。

2）从理论上讲，通过概念学习，每个模糊三支对可以得到16个模糊三支概念。但从实验结果可以看出，不同的不完备模糊三支概念可以得到相同的充要模糊三支概念。因此事实上，通过概念学习得到的模糊三支概念的个数小于或等于16。

5 结 论

三支形式概念分析实现了形式概念分析从双向决策到三支决策的扩展。但在现实生活中，除了传统的形式背景之外，还有很多模糊的形式背景。此时，三支形式概念分析不再适用。因此，本文提出了模糊形式背景下的模糊三支概念分析模型。在此基础上，本文提出了基于模糊三支算子的概念学习方法，实现了任意模糊三支对的概念学习。为了说明理论的正确性，本文进行了案例分析和实验分析。实验结果表明，通过文中所提出的模糊三支概念学习方法可以从普通的模糊三支对中获得模糊三支概念。

为了在模糊形式背景中实现三支概念的认知学习，本文提出了模糊三支形式概念分析的概念认知学习理论。不过，正如前述概念认知学习是一个新兴的交叉学科研究领域，虽然已取得阶段性的研究成果，但是还有很多方面的研究需要继续深入研究。例如，大数据环境下的概念认知增量学习问题、概念认知学习的不完全认知问题、通过认知主体自身的一些特点优化概念认知结果等等。这也正是在当前大数据科学和人工智能时代下概念认知学习领域需要进一步发展的重要方向。

参考文献：

［1］ 张文修， 徐伟华. 基于粒计算的认知模型［J］. 工程数学学报， 2007， 24（6）： 957-971.

ZHANG W X， XU W H. Cognitive model based on granular computing［J］.Chinese Journal of Engineering Mathematics， 2007， 24 （6）： 957-971.

［2］ XU W H， PANG J Z， LUO S Q. A novel cognitive system model and approach to transformation of information granules［J］. International Journal of Approximate Reasoning， 2014， 55（3）： 853-866.

［3］ XU W H， LI W T. Granular computing approach to two-way learning based on formal concept analysis in fuzzy datasets［J］. IEEE Transactions on Cybernetics， 2016， 46（2）： 366-379.

［4］ WANG Y X. On cognitive computing［J］. International Journal of Software Science and Computational Intelligence， 2009， 1（3）： 1-15.

［5］ YAO Y Y. Interpreting concept learning in cognitive informatics and granular computing ［J］. IEEE Transactions on Systems， Man， and Cybernetics-Part B： Cybernetics， 2009， 39（4）： 855-866.

［6］ LI J H， MEI C L， XU W H， et al. Concept learning via granular computing： A cognitive viewpoint ［J］. Information Sciences， 2015， 298： 447-467.

［7］ LI J H， HUANG C C， QI J J， et al. Three-way cognitive concept learning via multi-granularity ［J］. Information Sciences， 2017， 378： 244-263.

［8］ 王國胤， 李帅， 杨洁. 知识与数据双向驱动的多粒度认知计算［J］. 西北大学学报（自然科学版）， 2018， 48（4）， 488-500.

WANG G Y， LI S， YANG J. Knowledge and data driven multi granularity cognitive computing［J］.Journal of Northwest University （Natural Science Edition）， 2018， 48 （4）， 488-500.

［9］ ASWANI KUMAR C， ISHWARYA M S， LOO C K. Formal concept analysis approach to cognitive functionalities of bidirectional associative memory ［J］. Biologically Inspired Cognitive Architectures， 2015， 12： 20-33.

［10］米允龙， 李金海， 刘文奇， 等. 基于粒计算的概念认知学习［J］. 中国人工智能学会通讯， 2019， 9（7）： 29-33.

MI Y L， LI J H， LIU W Q， et al. Concept cognitive learning based on granular computing［J］.Communication of Chinese Association for Artificial Intelligence， 2019， 9 （7）： 29-33.

［11］ZHAO Y X， LI J H， LIU W Q， et al. Cognitive concept learning from incomplete information ［J］. International Journal of Machine Learning and Cybernetics， 2017， 8（1）： 159-170.

［12］XU C L， WANG G Y. Bidirectional cognitive computing model for uncertain concepts ［J］. Cognitive Computation， 2019， 11（5）： 613-629.

［13］TSANG E C C， FAN B J， CHEN  D G， et al. Multi-level cognitive concept learning method oriented to data sets with fuzziness： A perspective from features ［J］. Soft Computing， 2020， 24（5）： 3753-3770.

［14］苗夺谦， 张清华， 钱宇华， 等. 从人类智能到机器实现模型——粒计算理论与方法［J］. 智能系统学报， 2016， 11（6）： 743-757.

MIAO D Q， ZHANG Q H， QIAN Y H， et al. From human intelligence to machine realization model particle computing theory and method［J］.CAAI Transactions on Intelligent Systems， 2016， 11 （6）： 743-757.

［15］徐伟华， 李金海， 魏玲， 等. 形式概念分析理論与应用［M］. 北京：科学出版社， 2016.

［16］陈德刚， 徐伟华， 李金海， 等. 粒计算基础教程 ［M］. 北京： 科学出版社， 2019.

［17］魏玲， 万青， 钱婷， 等. 三元概念分析综述［J］.西北大学学报（自然科学版）， 2014， 44（5）： 689-699.

WEI L， WAN Q， QIAN T， et al. A review of ternary concept analysis［J］.Journal of Northwest University （Natural Science Edition）， 2014， 44 （5）： 689-699.

［18］SHIVHARE R，CHERUKURI A K， LI J H. Establishment of cognitive relations based on cognitive informatics ［J］. Cognitive Computation， 2017， 9（5）： 721-729.

［19］FUJITA H， GACTA A， LOIA V， et al. Resilience analysis of critical infrastructures： A cognitive approach based on granular computing ［J］. IEEE Transactions on Cybernetics， 2019， 49（5）： 1835-1848.

［20］FAN B J， TSANG E C C， XU W H， et al. Attribute-oriented cognitive concept learning strategy：A multi-level method ［J］. International Journal of Machine Learning and Cybernetics， 2019， 10（9）：2421-2437.

［21］米允龙， 李金海， 刘文奇， 等. MapReduce框架下的粒概念认知学习系统研究［J］. 电子学报， 2018， 46（2）： 289-297.

MI Y L， LI J H， LIU W Q， et al. Research on cognitive learning system of granular concept under MapReduce framework［J］.Acta Electronics Sinica， 2018， 46 （2）： 289-297.

［22］李金海， 米允龙， 刘文奇. 概念的渐进式认知理论与方法［J］.计算机学报， 2019， 42（10）： 2233-2250.

LI J H， MI Y L， LIU W Q. Progressive cognitive theory and method of concept ［J］.Chinese Journal of Computer， 2019， 42 （10）： 2233-2250.

［23］SHI Y， MI Y L， LI J H， et al. Concept-cognitive learning model for incremental concept learning ［J］.IEEE Transactions on Systems， Man， and Cybernetics： Systems， 2019， 1（1）：1-13.

［24］YAO Y Y. Three-way decisions and cognitive computing ［J］. Cognitive Computation， 2016， 8（4）：543-554.

［25］HUANG C C， LI J H， MEI C L， et al. Three-way concept learning based on cognitive operators： An information fusion viewpoint ［J］. International Journal of Approximate Reasoning， 2017， 83：218-242.

［26］FAN B J， TSANG E C C， XU W H. Attribute-oriented cognitive concept learning strategy：A multi-level method ［J］. International Journal of Machine Learning ＆ Cybernetics， 2019， 10（9）： 2421-2437.

［27］WILLE R. Restructuring lattice theory： An approach based on hierarchies of concepts ［J］. Orderd Sets D Reidel， 1982， 83：445-470.

［28］GUO L K， HUANG F P， LI Q G， et al. Power contexts and their concept lattices ［J］. Discrete Mathematics， 2011， 311（18/19）：2049-2063.

［29］ZOU L G， ZHANG Z P， LONG J. A fast incremental algorithm for constructing concept lattices ［J］. Expert Systems with Applications， 2015， 42（9）：4474-4481.

［30］LIU M， SHAO M W， ZHANG W X， et al. Reduction method for concept lattices based on rough set theory and its application ［J］. Computers ＆ Mathematics with Applications， 2007， 53（9）：1390-1410.

［31］PEI D， MI J S. Attribute reduction in decision formal context based on homomorphism ［J］. International Journal of Machine Learning and Cybernetics， 2011，2（4）：289-293.

［32］LI J Y， WANG X， WU W Z， et al. Attribute reduction in inconsistent formal decision contexts based on congruence relations ［J］. International Journal of Machine Learning and Cybernetics， 2017， 8（1）：81-94.

［33］SHAO M W， LI K W. Attribute reduction in generalized one-sided formal contexts ［J］. Information Sciences， 2017， 378：317-327.

［34］WANG L D， LIU X D. Concept analysis via rough set and AFS algebra ［J］. Information Sciences， 2008， 178（21）：4125-4137.

［35］KANG X P， LI D Y， WANG S G， et al. Formal concept analysis based on fuzzy granularity base for different granulations ［J］. Fuzzy Sets and Systems， 2012， 203：33-48.

［36］SHAO M W， LEUNG Y， WANG X Z， et al. Granular reducts of formal fuzzy contexts ［J］. Knowledge Based Systems， 2016， 114：156-166.

［37］LI J H， REN Y， MEI C L， et al. A comparative study of multigranulation rough sets and concept lattices via rule acquisition ［J］. Knowledge-Based Systems， 2016， 91：152-164.

［38］WU W Z， LEUNG Y， MI J S. Granular computing and knowledge reduction in formal contexts［J］.IEEE Transactions on Knowledge and Data Engineering， 2009， 21（10）：1461-1474.

［39］MA J M， ZHANG W X， LEUNG Y， et al. Granular computing and dual Galois connection ［J］. Information Sciences， 2007， 177（23）：5365-5377.

［40］WEI L， WAN Q. Granular transformation and irreducible element judgment theory based on pictorial diagrams ［J］. IEEE Transactions on Cybernetics， 2017， 46（2）：380-387.

［41］YAO Y Y. Interval sets and three-way concept analysis in incomplete contexts ［J］.International Journal of Machine Learning and Cybernetics， 2017， 8（1）：3-20.

［42］REN R S， WEI L. The attribute reductions of three-way concept lattices ［J］. Knowledge Based-Systems， 2016， 99：92-102.

［43］LI M Z， WANG G Y. Approximate concept construction with three-way decisions and attribute reduction in incomplete contexts ［J］. Knowledge-Based Systems， 2016， 91：165-178.

［44］GANTER B， WILLE R. Formal concept analysis ［M］. Berlin， Heidelberg：Springer， 1999.

［45］QI J J， WEI L， YAO Y Y. Three-way formal concept analysis ［M］∥Rough Sets and Knowledge Technology. Cham：Springer International Publishing， 2014， 8818：732-741.

［46］BURUSCO A， FUENTES-GONZLEZ R. Concept lattices defined from implication operators［J］.Fuzzy Sets and Systems， 2000， 114（3）：431-436.

（编 辑 张 欢）

作者简介：

徐伟华，男，西南大学人工智能学院教授，博士生导师。重庆市中青年骨干教师、重庆市十佳科技青年提名奖、重庆市巴南区学术技术带头人、重庆市数学会理事。国际粗糙集学会高级会员、中国人工智能学会粒计算与知识发现常务委员、中国人工智能学会知识工程与分布智能专业委员会委员、美国数学评论评论员、国家自然科学基金通讯评审专家、教育部自然科学奖评审专家。已在IEEETCYB，INS，FSS等国内外重要学术刊物上發表论110余篇，其中SCI检索70余篇（次），Web of Science引用1 500余次，H指数为21，其中3篇论文入选ESI高被引论文。出版学术著作4部，主持国家自然科学基金及省部级项目多项，获河北省自然科学三等奖1项。