误差在吸附测试方法和数据处理中的影响及其纠正

马青华 张学梅 郝静远,2 李 东

(1.西安思源学院能源及化工大数据应用教学研究中心，陕西 710038；2.西安交通大学化工学院，陕西 710038)

任何数据都需要通过实验测量来获取，无论是直接测量还是间接测量的参数在测量过程中都存在误差，并且间接测量的误差还会通过近似公式逐级传递至下一步，所以误差总是伴随着实验过程而不可避免地存在。在一定温度和压力下测量气体吸附量也是有误差存在。比如在等温吸附实验过程中，温度和压力要控制会有控制误差，吸附量要测量会带来测量误差。在用兰氏等温吸附方程进行处理吸附量数据会产生吸附模型自身与实际情况之间的理论误差。

虽然有学者讨论过吸附过程中产生的误差，但未见用大量实测吸附数据探讨吸附实验过程中存在哪些误差、来源及其可行的纠正方法。为此，本文将对上述问题进行研究，并且探讨能否通过选择更容易控制的实验装置，较少传递次数和较少实验次数来减少误差。

1 数据转换

1.1 实测吸附量

本文数据引用赵金等文章，页岩气(3个测试温度共36个实测吸附量)和煤层气(3个测试温度有18个实测吸附量)对于引用的在某温度某压力下实际测量到的吸附量，记为“吸附实测量”，样品数据均由相应文章作者经过实验所得，实验原理清楚，过程科学严谨。数据分析在合理区间，流程正确，并将此作为最基础的数据。

1.2 兰氏计算量

因为系列等温吸附数据数量比较大，所以绝大多数的研究文章都按国家标准用报道Langmuir等温吸附方程(兰氏方程)的参数(兰氏体积和兰氏压力)来代替报道系列等温吸附的实测吸附量。

Langmuir等温吸附方程：

(1)

式中：V为吸附量，cm3·g-1；a=VL为兰氏体积，cm3·g-1；b=1/pL为兰氏压力的倒数，MPa-1。

显然兰氏参数并不是直接测量得到的，而是通过实测吸附量按方程1进行回归计算而得到的。本文引用的不同温度下页岩与煤岩的兰氏参数分别列于表1和表2。

表1 不同温度下页岩的兰氏参数

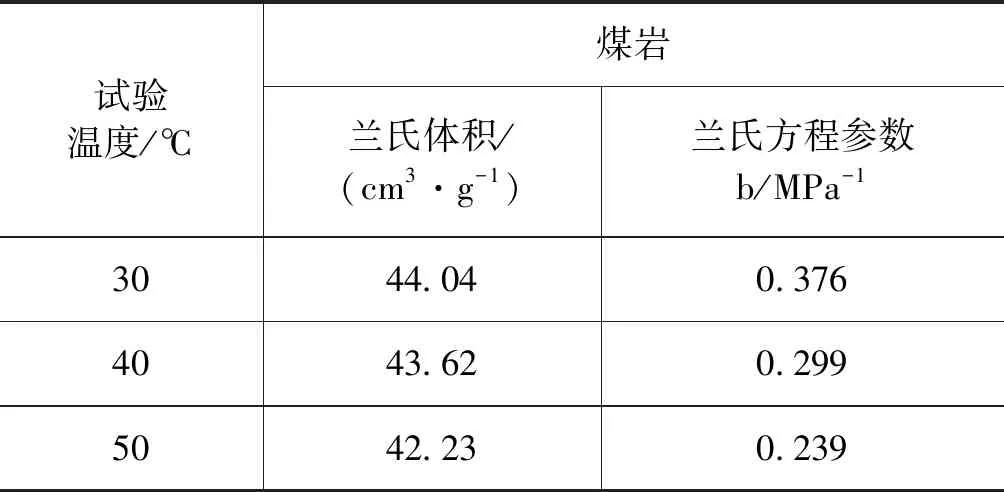
表2 不同温度下煤岩的兰氏参数

根据表1与表2的兰氏参数计算出与实测吸附量的温度、压力一一对应的计算吸附量，记为“兰氏计算量”。兰氏计算量与实测吸附量的差别包括第一级误差传递。

1.3 实测回归计算量

温度-压力-吸附方程(Temperature-Pressure-Adsorption Equation, TPAE)是一个包含温度、压力和吸附体积三个相互共存、互为影响变量的数学方程。

(2)

式中：A为微孔几何形体常数，无量纲；B为吸附流量系数，无量纲；M为吸附分子量；P为吸附压力，MPa；T为吸附温度，K；V为吸附量，cm3/g；β为压力影响的参数，无量纲；Δ为一个吸附分子的最低势能和活化能之间的能量差，K。

显然，温度-压力-吸附方程中的四个参数(A、B、β、Δ)不是直接测量得到的，而是按方程2通过回归计算(间接测量)得到的。如何根据回归样本群(吸附实测量或兰氏计算量)计算确定温度-压力-吸附方程中的四个参数(A、B、β、Δ)可以参考李东等有关论述。用吸附实测量为回归样本群回归计算出温度-压力-吸附方程的四个参数列于表3。将表3的有关参数代回方程2就得到与实测吸附量温度、压力一一对应的计算吸附量，记为“实测回归计算量”。实测回归计算量与吸附实测量的差别包括第一级误差传递。

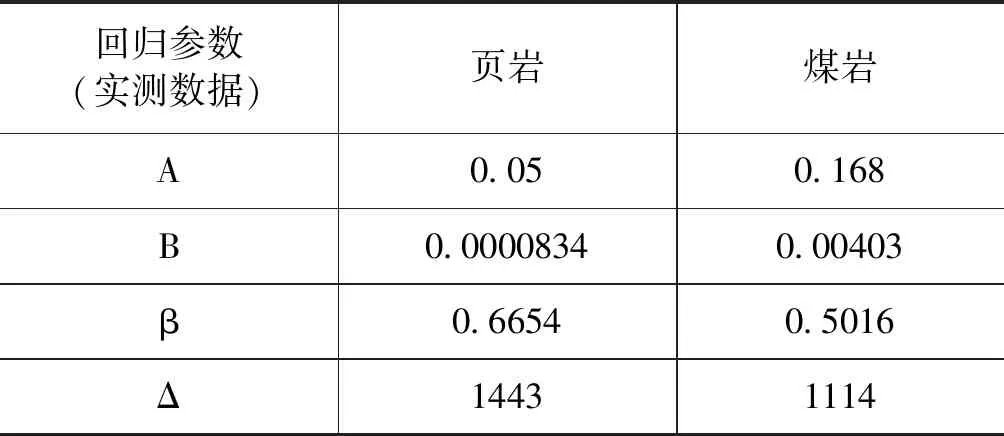
表3 根据吸附实测量为回归样本群得到温度-压力-吸附方程的参数

1.4 兰氏回归计算量

因为大多数的研究文章都按国家标准用报道Langmuir等温吸附方程(兰氏方程)的参数(兰氏体积和兰氏压力)来代替报道系列等温吸附的实测吸附量，那么在绝大多数情况下，只能用兰氏计算量作为回归样本群来代替实测吸附量以便于回归计算出温度-压力-吸附方程的四个参数。用兰氏计算量作为回归样本群得到的四个参数列于表4。将表4的有关参数代回方程2就得到相应温度、压力的兰氏回归计算量。兰氏回归计算量与吸附实测量的误差包括从实测吸附量到兰氏计算量的第一级误差，再加上从兰氏计算量到兰氏回归计算量的第二级误差传递。

表4 根据兰氏计算量为回归样本群得到温度-压力-吸附方程的参数

通过以上描述，对于煤岩或页岩，都各有四组温度-压力-吸附量的数据。这四组温度-压力-吸附量的区别在于：一组是吸附实测量，另外三组是吸附计算量。

这三组吸附计算量中：一组是根据兰氏等温吸附方程(方程1)计算，另外两组是根据温度-压力-吸附方程(方程2)计算。

而根据温度-压力-吸附方程(方程2)计算的两组中：一组是以实测吸附量为回归样本群，另一组是以兰氏计算量为回归样本群。

2 误差计算

(3)

参考赵金等，得出对于页岩，N=36；对于煤岩，N=18。

因为有四组(一组实测量、三组计算量)温度-压力-吸附量的数据，所以进行四个相对平均误差计算。为了便于区分，将四个相对平均误差计算按其基准组和比较组进行编号。这四个相对平均误差计算中，三个是将吸附实测量作为比较的基准组。因为本文的目的是计算并比较吸附测试方法和数据处理中的误差，所以规定一个“计算误差比”。计算误差比就是将最常见的“兰氏计算量”与“吸附实测量”的计算误差定为比较基准，100%。这样，其它的误差计算与最常见的计算误差的比较结果则是一目了然。表5列出页岩的相对平均误差和计算误差比。表6列出煤岩的相对平均误差和计算误差比。

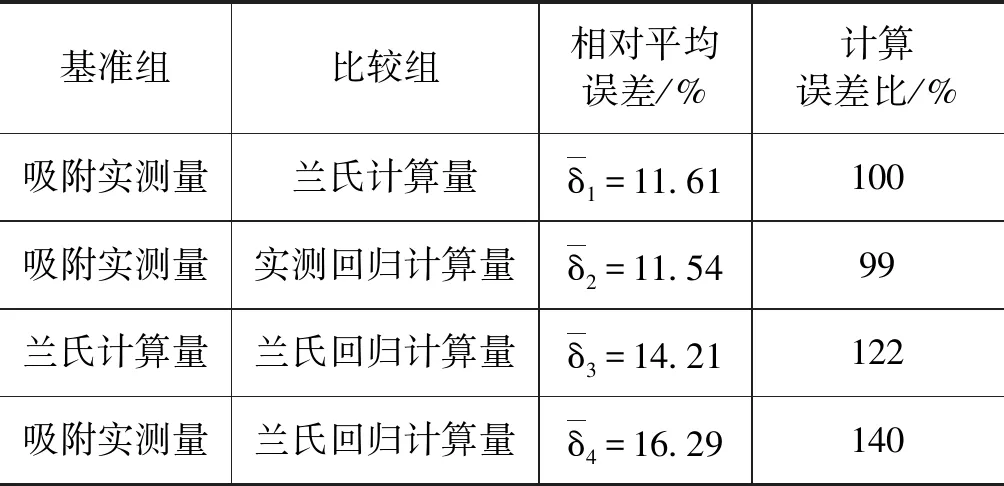
表5 页岩的基准组与比较组的相对平均误差和计算误差比

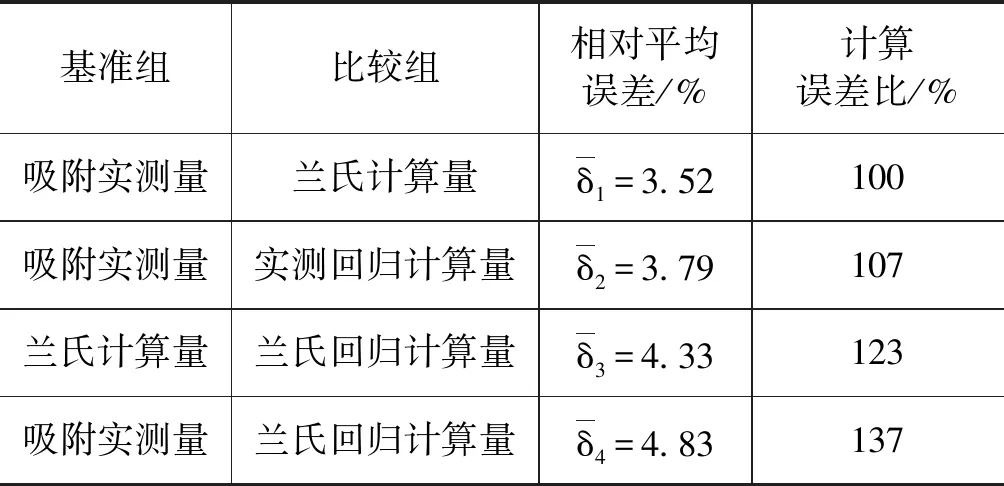
表6 煤岩的基准组与比较组的相对平均误差和计算误差比

3 结果与讨论

3.1 理论误差

误差一般分为两大类，理论误差和实验误差。理论误差来源于当研究的问题很复杂时，为了便于分析，往往采用对实际问题进行抽象、简化处理后的“物理模型”。对于兰氏等温吸附(单分子层吸附)理论的四个基本假设分别是：

(1)固体表面对气体分子只能发生单分子层吸附；

(2)固体表面是均匀的，所以摩尔吸附热不随表面覆盖程度的大小而变化；

(3)被吸附在固体表面上的分子相互之间的作用力可以忽略；

(4)吸附与解吸以相等的速率不断地进行而处于一个动态平衡。

大量吸附实验证实，单分子层等温吸附线只是五种吸附等温线类型中的一种，其余四种都是多分子层吸附等温线，包括BET多分子层吸附理论。还有等量吸附焓的实验证实：对于表面覆盖率不是很低时，被吸附的分子之间往往存在不可以忽略的相互作用力；另外，煤岩的等量吸附焓会随着表面覆盖率变化而变化。所以说，模型自身与实际情况之间的理论误差是存在的。因此实际吸附情况还是较兰氏等温吸附物理模型更复杂。

Freundlich等温吸附式并不具有Langmuir等温吸附式的物理模型，而仅是一个以指数方程为数学形式的吸附经验式以概括地表达部分吸附事实。而且多元函数指数方程的微积分比多元函数分数方程简单容易。抛开有无物理模型和纯数学计算的难易，有物理模型的兰氏等温吸附方程所产生的理论误差(表5和表6)和用经验吸附式的温度-压力-吸附方程所产生的理论误差(表5和表6)是一样的。就两者的平均值而言，经验公式的误差比物理模型的误差大3%，可以忽略不计。从相同的吸附实测量出发，用温度-压力-吸附方程所产生的理论误差与用兰氏等温吸附方程所产生的理论误差是一样的。前提是从相同的吸附实测量出发，因为相同的吸附实测量可以保证不同的数学方程，但实验误差、误差传递和比较标准都是相等的。

3.2 误差传递

直接测量不存在误差传递，误差传递只存在于间接测量中，并可以通过误差传递公式求出。兰氏等温吸附方程中的兰氏体积和兰氏压力，以及温度-压力-吸附方程中的四个参数(A、B、β、Δ)都是通过间接测量而得到的。理论上只要是从相同的吸附实测量出发，无论是按精确物理模型处理数据还是按经验公式处理数据，在计算误差上应该是相等的，但实际上差得很多。如表5中页岩的=16.29%，表6中煤岩的=4.83%。造成此类结果的唯一原因是误差的逐级传递，即包括了从吸附实测量到兰氏计算量的第一级误差传递再加上从兰氏计算量到兰氏回归计算量的第二级误差传递。由此可以得出一个结论：多于一级的误差传递可以导致误差的放大。

从表面上看，从兰氏计算量到兰氏回归计算量是只经过一次数学计算，也只有一级的误差传递，却比一级误差传递的大了许多。因为兰氏计算量是通过第一级误差传递而得到的。所以实际包含了“隐性”第一级误差传递再加上“显性”第二级误差传递，因此比真正的只有一级误差传递的误差要大就不足为怪。

3.3 实验误差

实验仪器的精确度产生的实验误差，测量仪器有测量仪器的测量误差，控制仪器有控制仪器产生的控制误差。虽然无法讨论所引用数据的实验仪器的精确度，但仍然可以得出：①多个元素(温度、压力)控制系统产生的控制误差一定大于单个元素(压力)控制系统产生的控制误差。②对于相同精确度的测量仪器，测量小值的相对误差一定大于测量大值的相对误差。比如说，这个系统会产生±0.2cm3/g的误差，对于总测量2cm3/g，相对误差为10%。而对于总测量20cm3/g，相对误差就仅为1%。

3.4 实验结果误差

实验结果误差是从实验开始操作到最终数据处理整个过程中所产生的误差。所以最终误差值的大小以及如何修改实验方案的可行性还得取决于实验结果误差。比较表5页岩与表6煤岩的四种相对平均误差值后可以看出：煤岩的相对平均误差值就比页岩对应的误差值小很多。也就是说，煤岩的计算吸附量更接近其实测吸附量。除了测量大值的相对误差一定小于测量小值的相对误差以外，在两个测量细节(起始测量压力和测量点数)上，煤岩是不同于页岩。

(1)起始测量压力，煤岩没有低于1兆帕的测量点，而页岩有；

(2)测量点数，同样是三个系列温度，页岩实测吸附量是36个，是煤岩测量点数(18个)的一倍。

因此起始测量压力和测量点数是修改吸附实验方案的重点。

4 改进的建议

(1)如果能从相同的吸附实测量出发，用温度-压力-吸附方程所产生的理论误差与用兰氏等温吸附方程所产生的理论误差是一样的。关于煤层气或页岩气吸附数据的处理选择使用温度-压力-吸附方程是完全可行的，是合理的。温度-压力-吸附方程描述温度、压力和吸附体积三个相互共存、互为影响变量的实际情况，并能解释吸附实验中发现的各种现象，如吸附温度的负影响、压力的正影响、二元吸附、吸附极大值、等量吸附焓等。

(2)与一般的化工吸附不同，对于低于1MPa时煤岩、页岩的吸附和解吸的精确表征在实际地下气体抽采中并不重要，页岩气吸附或煤层气吸附起始测试压力完全可以定为1MPa。

(3)按照国家标准的要求，为了求得恒温条件下的兰氏体积和兰氏压力，需要在该温度下测定一定(6～8个)的点数。但是如果按温度-压力-吸附方程来处理实测吸附量，则7个以上的不同温度、压力下的实测吸附量就可以精确表征该温度、压力范围内介质的吸附行为；所以完全可以采用诸如非常规变温变压吸附或非常规系列等温吸附来减少吸附测试点，但仍然可以达到精确表征温度-压力-吸附行为。

(4)除了保证样品测试前的平衡水以及测试必须达到动态平衡外，系列等温吸附必须精确控制等温。而变温变压吸附，除了保证样品测试前的平衡水以及测试必须达到动态平衡外，则不需要控制温度。

5 结论

通过以上对页岩气和煤层气的吸附实测量进行的吸附测试方法和数据处理中误差的影响及其纠正的研究，可以得出以下几点：

(1)吸附实验过程，特别是模拟地下的煤岩和页岩的吸附，不可避免会产生理论误差和实验误差。

(2)处理同一批吸附实测量，用温度-压力-吸附方程所产生的理论误差与用常见的兰氏等温吸附方程所产生的理论误差是相等的。

(3)因为所报道的兰氏参数都是经过吸附实测量的数学处理得到的间接量，所以用兰氏参数再进行的计算会产生误差传递。多于一级的误差传递一定导致实验结果误差的放大。

(4)为了使计算吸附量更接近于吸附实测量，同时也为了更精确表征介质在一定温度-压力范围内的吸附行为，建议制定一个统一的样品测试前的平衡水预处理程序，要求报告7个以上的变温变压(起始压力≥1MPa)吸附实测量，并用温度-压力-吸附方程来处理数据可以最大限度地降低实验结果误差。