投影机与球幕有效对比度白皮书
Claude Ganter (著) 贾 硕 (编译)
(1.美国Sky-Skan公司;2.中国科学技术馆,北京100012)
1投影机对比度
一般地,投影机原生对比度C的定义为完全饱和的白色图像 (RGB 编码的 (255,255,255))的亮度与黑色图像 (RGB 编码的 (0,0,0))的亮度(即残余背景照度)之比。测量照度时,投影机应未对其灯泡 (或其它类型光源)亮度进行任何动态控制(译注:关闭动态光圈、恒定灯泡功率)。
测量过程和计算都很简单,使用平面银幕,投射白色图像并测量照度。然后,在投影机继续以完全相同的方式工作时,透射黑色图像,并在银幕上的相同位置进行第二次测量。例如,如果测得白色画面照度为1000 lx,黑色画面照度为0.4 lx,则对比度为2500∶1。
之所以要使用平幕,是因为制造商使用的是“开放视场”(open field)概念,这意味着从房间反射出来的任何光都不应照回到银幕上。与外部世界的影响完全隔离的环境下,测量出的投影机对比度是一个理想值,因此称为“投影机原生对比度”。
实际上,只需要排除杂散光源或其它恒定光源不必要的照明影响就可以准确测得原生对比度。因为来自投影机灯泡的反射与其自身的光强度成正比,因此当用白色画面照度除以黑色画面照度时,房间的影响会自动消除。因此,使用其它任何形状的银幕,都可测出正确的原生对比度。
值得一提的是,其他方法也是可行的。
“ANSI对比度”测量的是平面银幕上50%棋盘格测试图的对比度。但是由于图案与投影机部件(成像面板、镜头等)之间可能存在相互影响,因此该测量方法(通常不会测出很高的对比度)难以操作。同样ANSI对比度似乎与天文馆的观影体验不太相关,因为观众在天文馆内可能会更适应暗场,并可以直接感知全黑信号时的黑暗程度。
因此在本文中,我们仅使用 “原生对比度”一词来表征投影机的对比度。
原生对比度也称为 “开/关对比度” (尽管从技术上讲,“关”在测量时投影机仍为 “开”),或者甚至更混乱地称为“动态对比度”,尽管此处不允许动态控制。术语 “动态”仅表示将白色和黑色的度量接连进行,并在时间上分开。
以下是一些制造商关于亮度和原生对比度C的最佳值/估计值,我希望这些值是可以接受的,因为我们的主要目标是显示这些数值与天文馆球幕是如何相互影响的,而不是确定确切的数值。
为了方便讨论,我们根据投影机对比度划分出3个类别,每类取一个型号做代表:
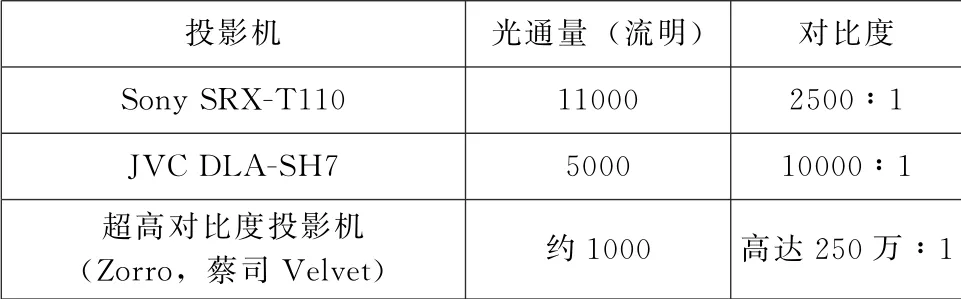
表1 三类典型对比度的投影机基本数据
2 球幕对比度
球幕对比度的理论推导,可以参考照明行业中用于测量光源强度的积分球理论 (也称光度球、光通球),该理论与计算方法已相当完善。
简单地讲,该理论假定一个复杂的图案发出的光朝各个方向传播,通过对空腔球体中光的多次反射求和就可以进行积分。球体还充当模糊设备,通过在一个位置的单个测量值就可以估算发射光的总能量。
进行这种计算的前提条件是假设球体的表面像朗伯反射器(或漫反射器)一样工作。
朗伯材料很容易在日常生活中见到。想象一面喷涂无光漆 (matte paint)墙面,四处走动很容易发现光在各个方向上是近似一致的。再想象,一面黑色的墙壁上有一片白色正方形的喷有无光漆的区域,则当您从其侧面测量时,测得的反射光亮度会下降,因为反射光仅从一个较小的角度范围内射出。当测量角度足够小,且仅在白色方块范围内进行点测,测得的亮度又是不变的。
球体中的每个朗伯体微元的反射光,向球内其它任意微元发射的光量相等。这种 “魔术”性质是由几何定律决定的,该定律确定了立体角,距离平方反比定律决定了发光能量。其实,除了知道球体是朗伯体,没有什么玄妙的,只是自然规律在起作用。
然而,工业上发明积分球的初衷是想通过光在球内壁的多次高效反射来提升光源亮度。而天文馆恰恰不需要这种反射带来的亮度放大,他们要提高对比度,这个改变需要花费一番努力,下面将会讨论。虽然我们的目标大相径庭,数学基础却是一致的。
将第一次反射产生图像的光能强度归一化为1,球冠状的银幕的放大因子A 就表示多次额外反射产生的光能与其之比。以下公式将光的多次衰减反射表达为一个无穷幂级数:
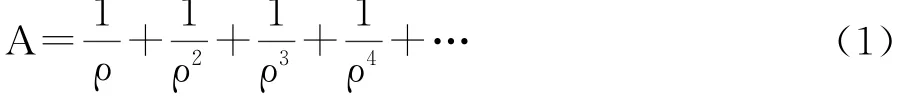
可用如下形式表示:

其中,

r是球幕的反射系数 (或增益),c是被照亮的球幕面积(球体的一部分)。
当讨论球幕反射系数 (或增益)r时,需要注意的是,银幕表面通常有透声孔,增益指的是根据其带来的反射面积损失修正后的带有涂料的幕板的反射率。例如,如果涂料反射了60%的光,而透声孔的面积占球幕面积的20%,则球幕的实际银幕增益为48%,即0.6 乘以0.8,然后以百分比表示。需要注意是,球幕制造商提供的球幕增益信息中包含了透声孔的影响。
对于天文馆中球幕,可以根据球幕开角Θ 计算球幕面积c。这就需要将立体角微元在球面上积分,表达式为:


表2 不同开角的球幕面积占整球面积比例对照表
表3 显示球幕的亮度放大率如何随球幕增益(来自涂料和透声孔的综合影响)和球幕开角的影响而变化。注意,放大率可以高于100%。
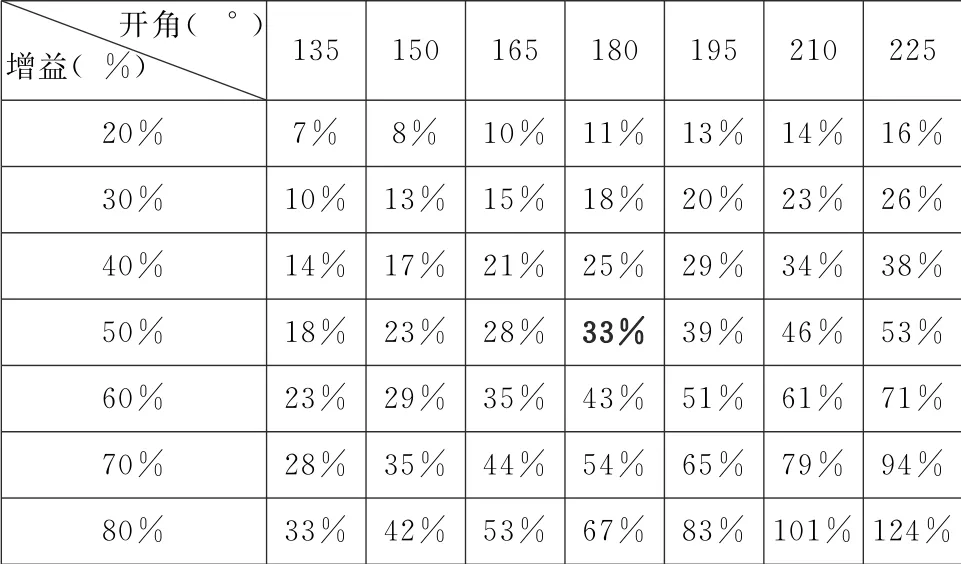
表3 球幕亮度放大率表
从表3中可以看出,增益为50%,开角为180°的球幕画面亮度增加了三分之一(33%)。由于球幕上的多次后续反射增加的这33%要加到第一次反射光的强度上(已归一化为100%),因此,与在平面银幕上的测量值相比 (当然假设在相同的距离上测量),这确实是一个非常明显的影响。在此示例中,如果我们在平面银幕上使用亮度计测量出亮度为10.0cd/m,那么在球幕上将测得13.3cd/m。
后续的反射光不含有初始图像信息 (由第一次反射光携带)。亮度的放大是均匀分布的,它会叠加到第一次反射形成的图像上面,这是光在球体内多次反射造成的。
假设我们投射的球幕画面在图像的某处带有一个小的黑色圆形。由于圆形面积非常小,因此不会改变白色画面中13.3cd/m的亮度。但是在黑色圆形内,我们只能测得经球幕反射放大出的额外亮度,即3.3cd/m。将这两个数字相除即可得出全球幕的对比度,在我们的示例中对比度就是4∶1,下面是一般表达式:

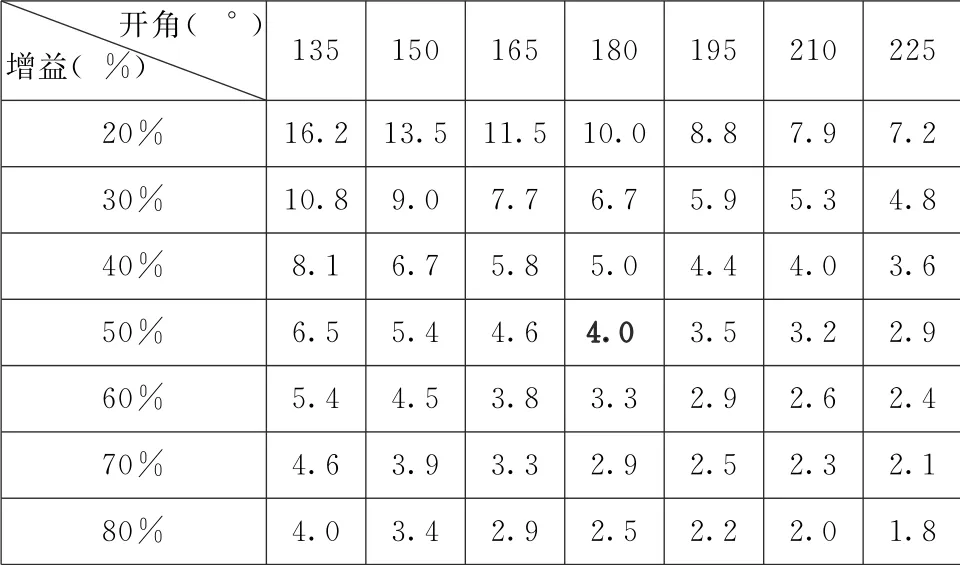
表4 全球幕对比度表
让黑色圆形面积增大继续推导。投射一个棋盘格测试图,它由相等数量的纯白色(100%)正方形和纯黑色(0%)正方形相间组成,球幕对比度如何变化?
在这种情况下,第一次显示的图像反射会模糊(由于多次反射亮度叠加,“积分”的影响),反射光以相同的量照到所有正方形上。这样我们就可以分两个部分计算:
①白色方块的亮度为1+0.5×A
②黑色方块的亮度为0+0.5×A
取值0.5是由于棋盘中白色方格覆盖了全球幕画面中的50%。由此可知,棋盘格测试图的球幕对比度C等于①除以②的比值:

从表5中可以看到,投影在球幕上的棋盘格图像在增益为50%、孔径为180°时,对比度为7∶1。继续前面的示例,我们将在白色正方形中测得11.67cd/m,在黑色正方形中测得1.67cd/m。
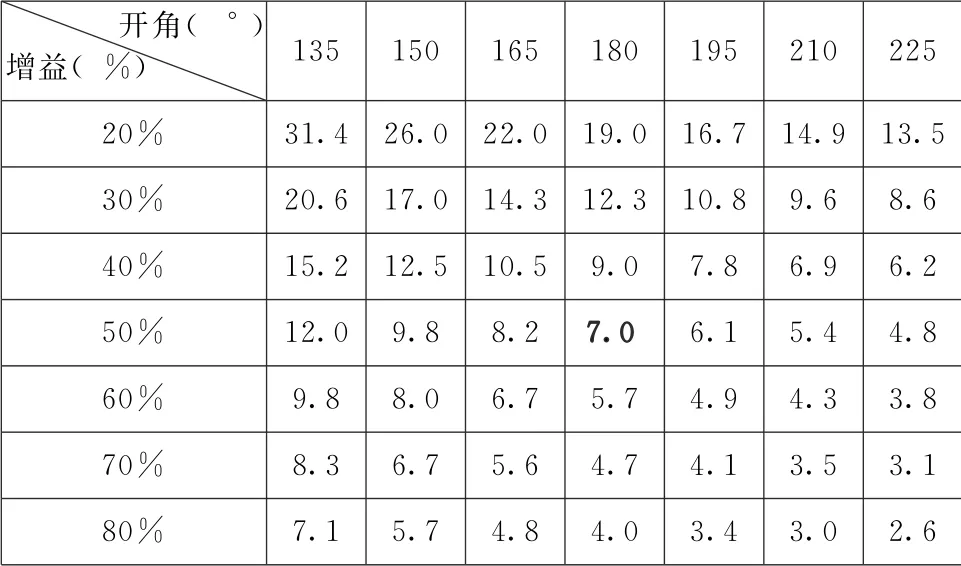
表5 棋盘格测试图对比度表
从某种意义上讲,这种球幕对比度的测量类似于投影机的ANSI测量方法,也适用于球幕。这些测量可在同一时刻进行,因此也被称为 “静态对比度”。
本节中推导没有考虑投影系统的影响。
通常,改善全球幕和棋盘格图案对比度的简单做法是:
(1)使用较低反射系数的涂料;

图1 黑色小圆形:(左)投射画面原图,(右)使用等立体角鱼眼镜头投影效果图r=50%,Θ=180°,f=0.999,Cd=4.0黑色圆形内不再是纯黑色
(2)如果可能,使用较小开角的球幕 (小于180°,更接近平幕)。
当然,人们通常不会在球幕上显示棋盘格,而会投射真实的图像。除了爆炸这样的场景外,可以说大多数图像的光要少得多。
一个重要的概念是,我们这里不讨论场景反射率的本质。实际上这更像是一个摄影场景,其动态范围经过压缩和裁剪,适合可用范围 (8位RGB 0至255)。此外,数据值 (例如JPEG 文件)和投影亮度之间的关系应遵循sRGB等相关标准。

图2 棋盘格测试图:(左)投射画面原图,

表6 sRGB投影亮度表以及一些有用的值
如果用数码相机从一个均匀区域拍摄照片,从生成的JPEG 文件中通常可以发现,所有点的最高值在大约在124级,换句话说,预期的投影亮度约为20% (投影机最高亮度的五分之一)。此结果随相机曝光校准和制造商JPEG 引擎的不同而不同,但是这种情况在很多品牌的产品中都有体现,所以可以假设我们找到了一个方便的标准,用于平均场景投影亮度。
我们称此场景投影亮度为填充因子。摄影场景的填充因子在不同图片之间会有很大不同,但是平均而言,我们可以说相机期望一个场景在投影设备上的填充因子约为20% (或0.2)。可以说我们期望80%的像素为黑色,而只有20%的像素为白色。的确与棋盘格测试图的情形完全不同(更好)。
如果f是如上定义的填充因子,则球幕对比度C的一般表达式为:

换言之,填充因子在最小0 (黑色图像)和1(全白色图像)之间调节着输入光的总能量,从而限制了放大量。因此,随着填充因子变小,球幕图像的对比度会变高。
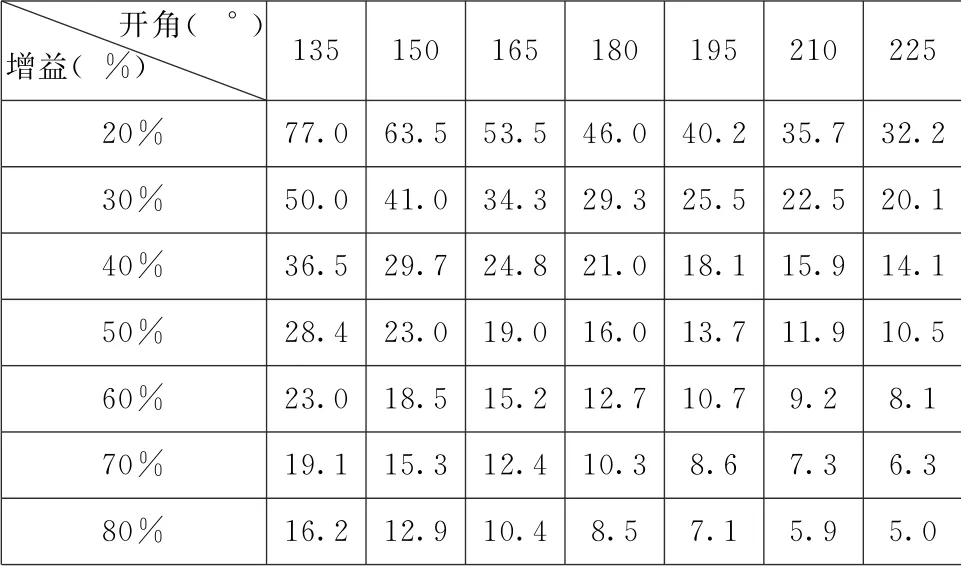
表7 标准对比度表 (填充因子=0.2)
表7之所以重要,是因为它给出了真实生活场景在球幕中的对比度。r=50%和Θ=180°的球幕的标准对比度为16∶1,这并不是很好。
通常的做法是,艺术家们对发行的全球幕节目画面进行分级(增强对比度),让投影出的节目看起来仍然不错。

图3 影片 《莫纳克亚山》(Mauna Kea):(左)球幕原始图,(右)等立体角鱼眼视图r=50%,Θ=180°,f=0.167,Cd=18.9请注意圆心处,由于交叉反射导致图像对比度急剧下降
下面对天象节目的情形加以分析:
假设我们在球幕上渲染了1000万像素。在常见的小型充气球幕影院中,月球和行星占据约1000像素(2平方度)。如果我们添加8000 颗星,每颗星由一个全亮像素表示,即添加了8000像素。考虑到5%面积的球幕上显示0.2%亮度的银河系,相当于添加了1000个白色像素 (1000万×0.05×0.002)。与可用的1000 万像素相比,所有这些像素相当于10000个全亮像素(1000+8000+1000)。占比就是0.001 (或0.1%)。
因此,对于使用数字天象系统渲染的常见天象节目的场景,假设填充因子为0.1%是基本合理的。
在这个星空场景中加上航天器或全景图,填充因子很容易达到2%,对于天象节目中展示的大多数的“太空艺术”画面而言,这个估值是足够的。
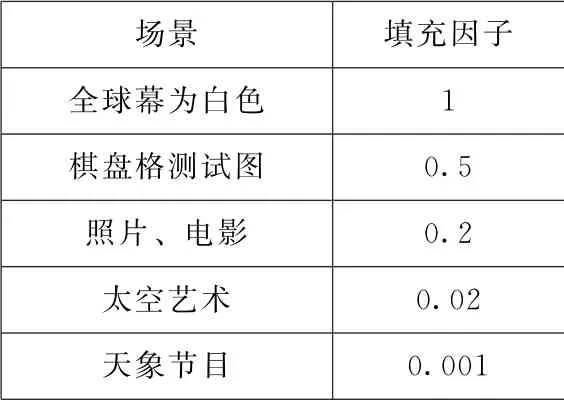
表8 根据场景分类的粗陋尝试
其实这里“太空艺术”和 “天象节目”估算的填充因子是有问题的。这是因为对比度会受到我们尚未考虑的投影机原生对比度的影响。但是,对于填充因子0.2或更高的情况,先前计算的表格数据显然还是可靠的。
当然还是要解决此问题,以确保计算可靠。
在下一部分中,我们将投影机和球幕的因素考虑进来计算有效对比度。
3 投影机与球幕有效对比度
在本节中计算更加复杂,把投影机的因素考虑进来并不会提升球幕对比度,只会使其变得更低。根据经典投影光学,光只会是相叠加增强的而不会相消。
求出球幕有效对比度很重要,它可以让我们看出不同投影技术之间的差异。另一方面,选择更优参数的方案会获得更好的效果。
我们将C称为有效对比度,它是考虑了投影机和球幕的影响的实际对比度。
我们将黑度B定义为黑的程度和白的程度之比(归一化为1)。显然,它就是投影机原生对比度的倒数:

这个数字通常很小,例如对于2500∶1的原生对比度,B=0.0004。
我们需要根据画面的黑暗程度的影响来修正填充因子。修正后的填充因子f只能在最小值B和最大值1之间变化:

然后,还须修改主要的对比度表达式,因此B出现在分母中:

让我们看看先前定义的标准对比度表 (填充因子=0.2)在原生对比度为2500∶1的投影系统中如何变化:
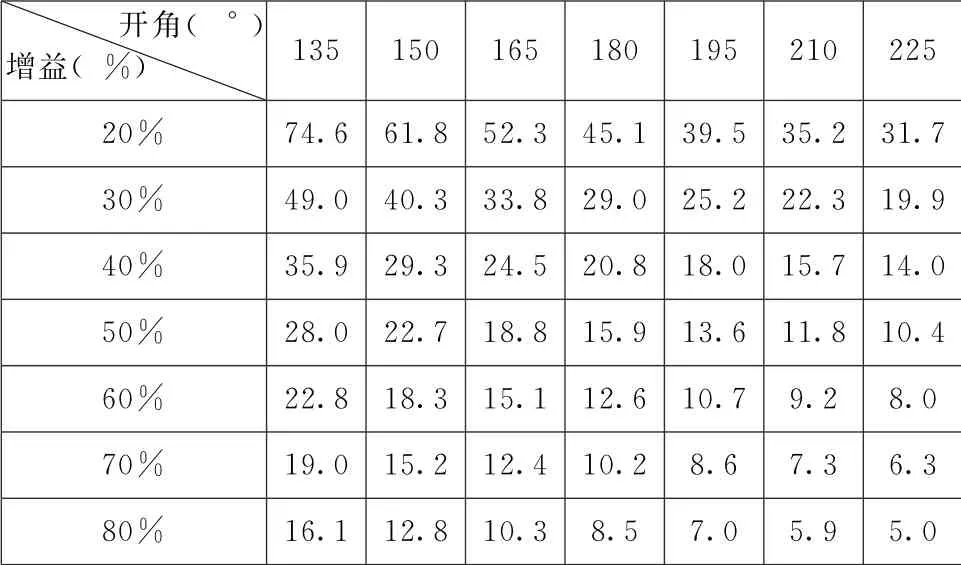
表9 原生对比度为2500∶1的球幕投影系统的标准对比度表 (填充因子=0.2)
正如预期的,与表7相比表9几乎没什么变化。对于“照片/电影”等“标准对比度”应用,其填充因子通常为0.2,这只是确认选择高对比度投影仪没有实际优势。
3.1 “太空艺术”节目的有效对比度
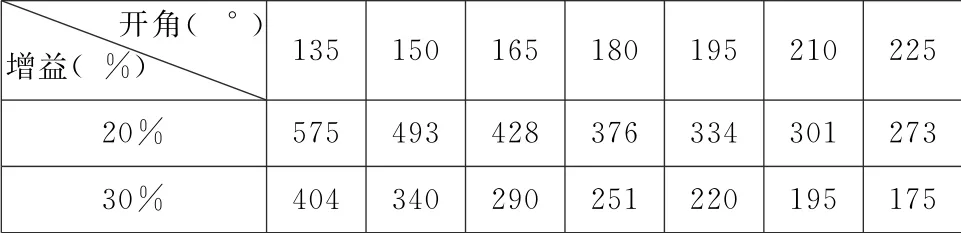
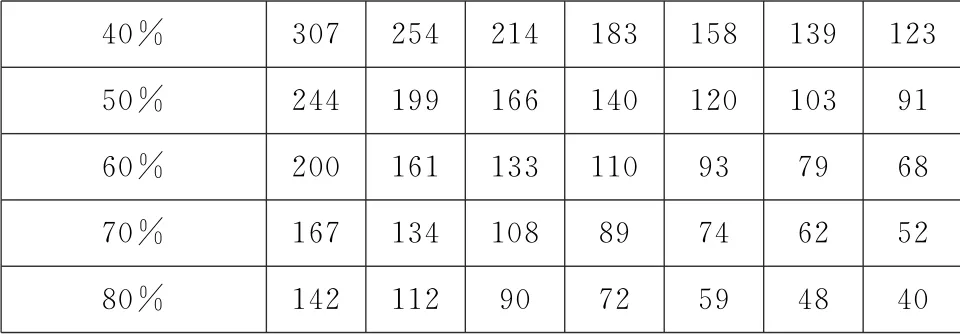
表10 原生对比度为2500∶1的球幕投影系统播放的“太空艺术”节目 (填充因子=0.02)的对比度表
40% 307 254 214 183 158 139 123 50% 244 199 166 140 120 103 91 60% 200 161 133 110 93 79 68 70% 167 134 108 89 74 62 52 80% 142 112 90 72 59 48 40
“太空艺术”节目的填充因子大约为2%(0.02),并且有可能出现更大的差异。我们先用相同的2500∶1 对比度的系统进行计算,再对2500000∶1对比度的系统进行计算。
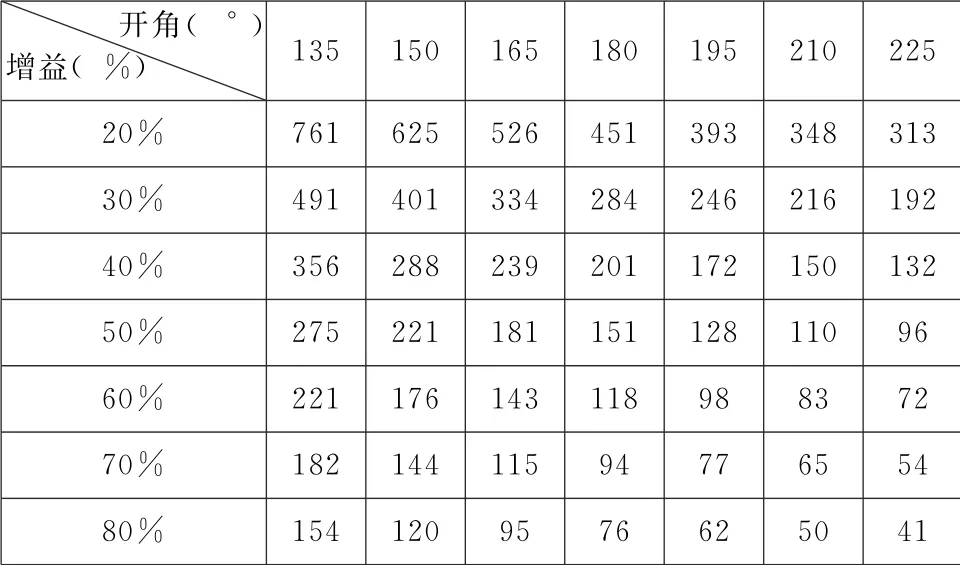
表11 原生对比度为2500000∶1的球幕投影系统的“太空艺术”节目 (填充因子=0.02)的对比度表

图4 影片 《哈勃》:(左)球幕原图,(右)等立体角鱼眼视图r=50%,Θ=180°,f=0.0134,Cp=2500,Ceff=201

图5 与图4条件相同,但亮度已提高10倍来看清黑的程度
与使用2500∶1 对比度的系统相比,使用2500000∶1对比度的投影系统时,有效对比度的确提高了8% (对增益为50%,开角180°的球幕)。但很明显,无论使用极低还是极高的原生对比度的投影机,在上述环境下的表现差别不大。

图6 影片 《哈勃》:(左)球幕原图,(右)等立体角鱼眼视图r=50%,Θ=180°,f=0.0134,Cp=2500000,Ceff=225

图7 与图6条件相同,但亮度已提高10倍来看清黑的程度
3.2天象节目的有效对比度
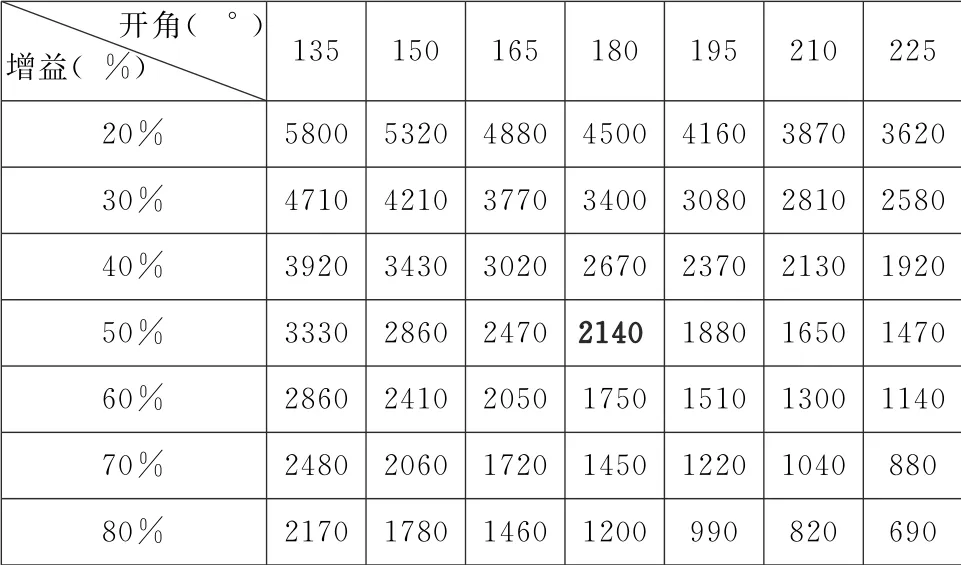
表12 原生对比度10000∶1的投影系统的天象节目 (填充因子=0.001)对比度表
天象节目的画面填充因子可以低至0.1%(0.001)。这个讨论非常重要,因为天文馆需要良好对比度来让观众感受到真实的星空,这是用户的核心需求。实际上,一般天文馆是不会选择2500∶1的投影系统的。因此10000∶1和2500000∶1系统的比较结果更为重要。
让我们看一下两个高对比度系统之间的比较。
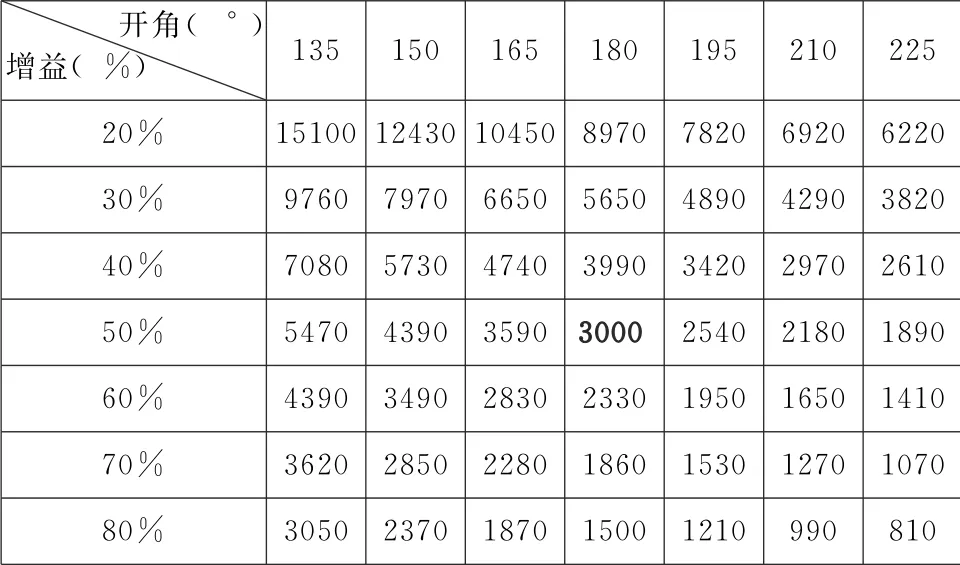
表13 原生对比度2500000∶1的投影系统的天象节目 (填充因子=0.001)对比度表

图8 星点测试图:(左)圆幕原图,(右)等立体角鱼眼视图r=50%,Θ=180°,f=0.0011,Cp=10000,Ceff=1958

图9 与图8条件相同,但亮度已提升10倍以看清黑的程度
这次有更大的差别。显然,投影机原生对比度2500000∶1的系统以3000∶1的有效对比度 (增益50%,180°球幕)胜出,而原生对比度10000∶1的系统则以2140∶1的有效对比度惜败。
但从视觉感受上对比,二者有效对比度的差别(28.7%)远没有投影机的原生对比度的差别 (250倍)来的大。只有在球幕开角非常小 (更像平幕)、非常暗的画面的条件下才能真正表现出超高的对比度(这一般是做不到的)。

图10 星点测试图:(左)圆幕原图,(右)等立体角鱼眼视图r=50%,Θ=180°,f=0.0011,Cp=2500000,Ceff=2645

图11 与图10条件相同,但亮度已提升10倍以看清黑的程度
3.3 球幕增益优化对对比度影响
实际上,如果球幕增益可以从50%降低到30%,则10000∶1对比度的系统可以达到3400∶1的有效对比度。这是一个非常现实的折衷,因为此类投影机的亮度通常为超高对比度投影机亮度的五倍。
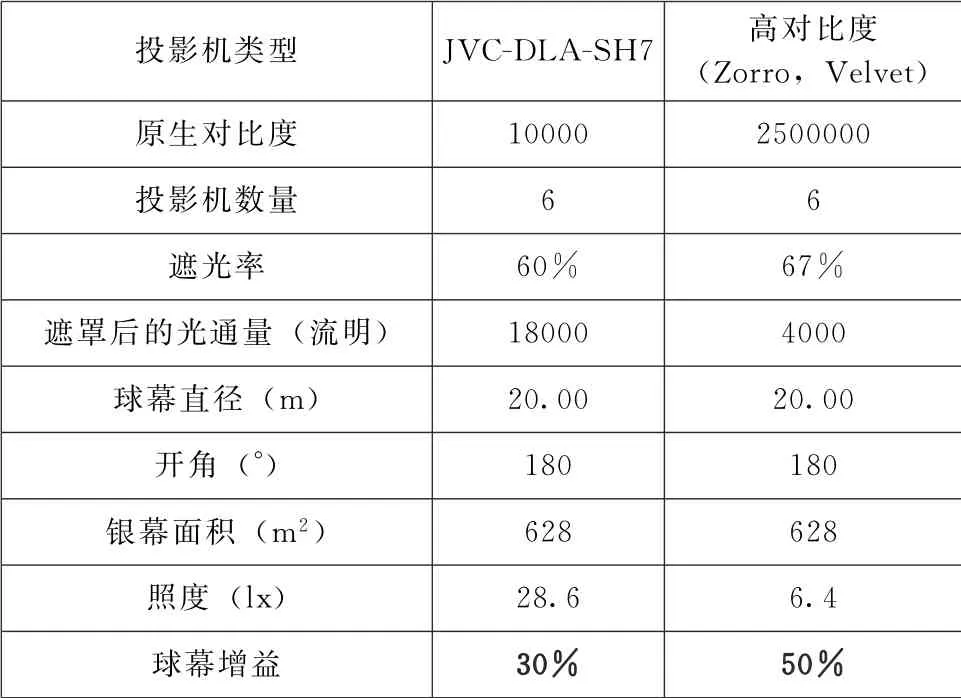
表14 两个高对比度系统的一种可行的优化方案
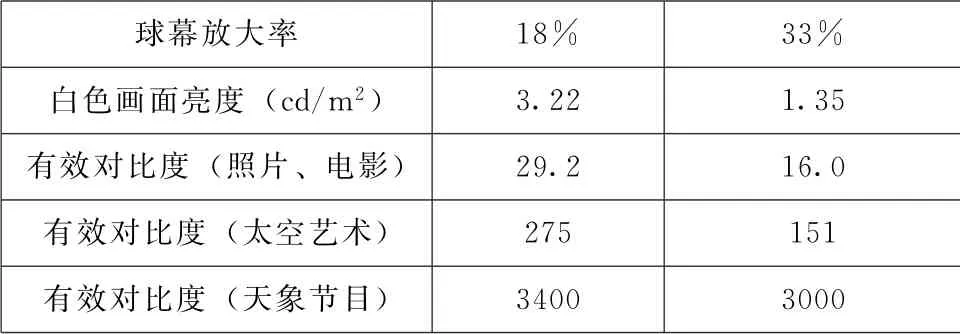
球幕放大率 18% 33%白色画面亮度 (cd/m2) 3.22 1.35有效对比度 (照片、电影) 29.2 16.0有效对比度 (太空艺术) 275 151有效对比度 (天象节目) 3400 3000
可见,降低球幕增益的效果对实际结果具有极大的影响。
我们发现10000∶1对比度的系统是最佳的折衷方案,因为较高的亮度允许我们选用增益更低的球幕。包括天象节目在内的所有的情形下,有效对比度都可以更高,同时保持两倍或更高的亮度 (还有更好的色彩)。
3.4 极高对比度的投影机具有优势的情况
(1)显然,只有在球幕上不显示任何画面,且假设不存在其他杂散光源时,超高对比度投影机才会表现更好(这是唯一可以 “看到”原生对比度的情况)。
(2)此外,当使用亮度非常低的光学天象仪授课时,在较暗处会显示出一些优势 (但当用数字系统投射某些内容,较低的亮度会影响观众对色彩的感知,且有效对比度会下降)。
(3)现有高增益球幕无法升级替换掉的情况(然而,大多数场景下还是不能真正提升对比度,花在投影机上的额外投资须与新球幕的成本进行比较)。
4 结论
本文建立了一种考虑投影系统和球幕的共同影响,可准确计算有效对比度的方法。
主要结论是,包括天文象节目在内的所有实际使用场景,对比度为10000∶1的数字投影机都是目前最好的解决方案。理由是,考虑所有实际条件,这个配置都可以在高亮度与球幕增益之间取得平衡,来获得最佳对比度。
当对比度为2500000∶1的投影机在亮度和成本都接近10000∶1对比度的投影机时,超高对比度投影机才可能得到更广泛的应用。
当然,人们会思考是否这就是球幕环境中对比度控制问题的最佳解决方案。
注释
①本文作者Claude Ganter生于1959年,1989年在法国的路易·巴斯德斯特拉斯堡大学研究采用红外光谱和核技术分析硅材料,获博士学位;曾在法国巴黎发现宫 (Palais de la Découverte science museum)任研究工程师;曾任职法国布列塔尼天文馆馆长12 年,期间开发出一套数字天象系统,可在Windows网络上运行;2001年起在美国Sky-Skan公司任科学部主任,从事软件算法研究,擅长数字天象系统光学设计。
②在工业生产过程中,投影机对比度的实际测量会按照比本文提出的方案更为复杂的ANSI标准进行。通常使用九个测量点的方法,但实质上是开启了动态对比度 (开/关方法)测得的。
③如前所述,白皮书的推导是基于业内公认的用于光源测量的“积 分 球” 理 论。 下 面 是 更 为 详 尽 的 介 绍:http ∶//www.labsphere.com/uploads/technical-guides/a-guide-to-integratingsphere-radiometry-and-photometry.pdf。本文尽量避免数学推演。3.2节应该可以满足最苛刻的读者的要求,因为它包含了能量传递不变性 (我们称为 “魔术”性质)的完整说明。
④下面是有关sRGB标准的信息,文献介绍了gamma转换是如何将sRGB 数据转换为线性域的:http∶//en.wikipedia.org/wiki/SRGB。
⑤我们使用Photoshop CS6 来为我们的文章制作配图。尽管Photoshop并不是用于科学研究的工具,但它可以用于使用自定义色彩空间 (简化伽玛值或线性CIE 6500K)进行线性图像数据处理。
附录A:
模拟图片的制作步骤:

表A1 模拟表格r=0.5,Θ=180°,Cp=10000∶1
目前,市面发行的全球幕节目拷贝的画面一般为4K 分辨率图片序列帧,每个颜色8位,我们按此进行模拟。本文中使用了一些测试图,例如小圆孔或星空。我们用Photoshop来完成下面步骤的制作:
第1 步:打开图片,如果需要,指定一个“sRGB”色彩空间标签,并转换为每个颜色16位,保存图片;
第2步:将等距图片转换为等立体角投影。这是确保球幕画面面积与原图有线性关系的必要条件;
第3步:将sRGB 颜色配置文件转换为简化的RGB灰度系数1,以模拟投影机的亮度 (线性数据)。使用选择工具和直方图,测量光度当做填充因子(30%红色,59%绿色,11%蓝色,通常建议对每种颜色进行单独处理,但此处没有必要);

图A1 用于模拟天象节目的星空图案
第4步:计算此图片的白色和黑色有效亮度,作为本文定义的有效对比度C计算公式中的分子和分母。导出校正值用于图像的曝光和补偿。如果需要,曝光校正可以避免饱和,而补偿值能模拟出背景交叉反射的影响;
第5步:转换回sRGB 颜色空间。如果需要提高清晰度,可将亮度提高3.32档 (10倍),将其调整为0.5K 分辨率,使用抖动分配转换为8位。
下面以星空图案为例,生成4K 分辨率图案的详细步骤:
用一张边长为500像素的正方形图片平铺生成4K (边长为4096像素)球幕原图,用于对天象节目进行模拟。在gamma值为1的RGB 色彩空间中测量时,此正方形的填充因子f为0.11%。

