简单链形悬挂接触网动力学性能仿真实验
胡 艳,黄盼盼,马 然
(江苏师范大学 机电工程学院,江苏 徐州 221000)
0 引 言
人才培养是高等教育的落脚点和出发点,而高质量的人才培养又离不开科研的支撑。在教学过程中,构建寓教于研的人才培养模式,一方面有助于提高学生学习兴趣,形成学习中参与科研,科研中深化学习,教学与科研良性互动的机制,另一方面有利于形成高水平科研与高质量人才培养同步提升的理想状态[1]。
接触网沿轨道方向“之”字形架设,通过受电弓与接触网间的滑动电接触为列车提供电能,是电气化高速铁路的重要组成部分[2-4],其结构参数设计是否合理对列车运行极限速度有重要影响[5-7]。高速铁路接触网系统目前仍是国内外研究的焦点之一。我国运用较多的接触网分为简单链型悬挂和弹性链型悬挂两种[8]。其中,简单链型悬挂接触网广泛应用于城际铁路和普速铁路。我国第一条时速350 km的城际铁路京津城际铁路即是采用简单链型悬挂接触网系统[9-10]。
针对简单链型悬挂接触网设计了“简单链形悬挂接触网动力学性能仿真实验”,为学生学习过程中参与科研,科研中强化学习提供了一个平台。通过该仿真实验,向学生展示了接触网系统的仿真过程,直观呈现了参数变化对系统动力学性能的影响,有利于激发学生学习的兴趣,一方面有助于增强接触网动力学的理论和实验教学效果,另一方面有助于培养学生的科学素养和实践创新意识。
1 接触网系统
如图1所示,接触网系统主要由接触线、承力索、吊弦、支柱、腕臂(支撑杆)、定位器等部件组成。接触线与受电弓滑板直接接触为列车提供电能;承力索通过整体吊弦悬吊接触线,通过调整整体吊弦的长度可以保证接触线的高度并改善接触悬挂的弹性;承力索通过腕臂固定在支柱处。定位器可使接触线在直线区段呈“之”形分布,使受电弓滑板均匀磨耗[11-13]。既有线路提速改造、新建线路铺设前须对设计方案中接触网的动力学性能进行评估,在进行试验验证之前都需要进行数值模拟仿真。
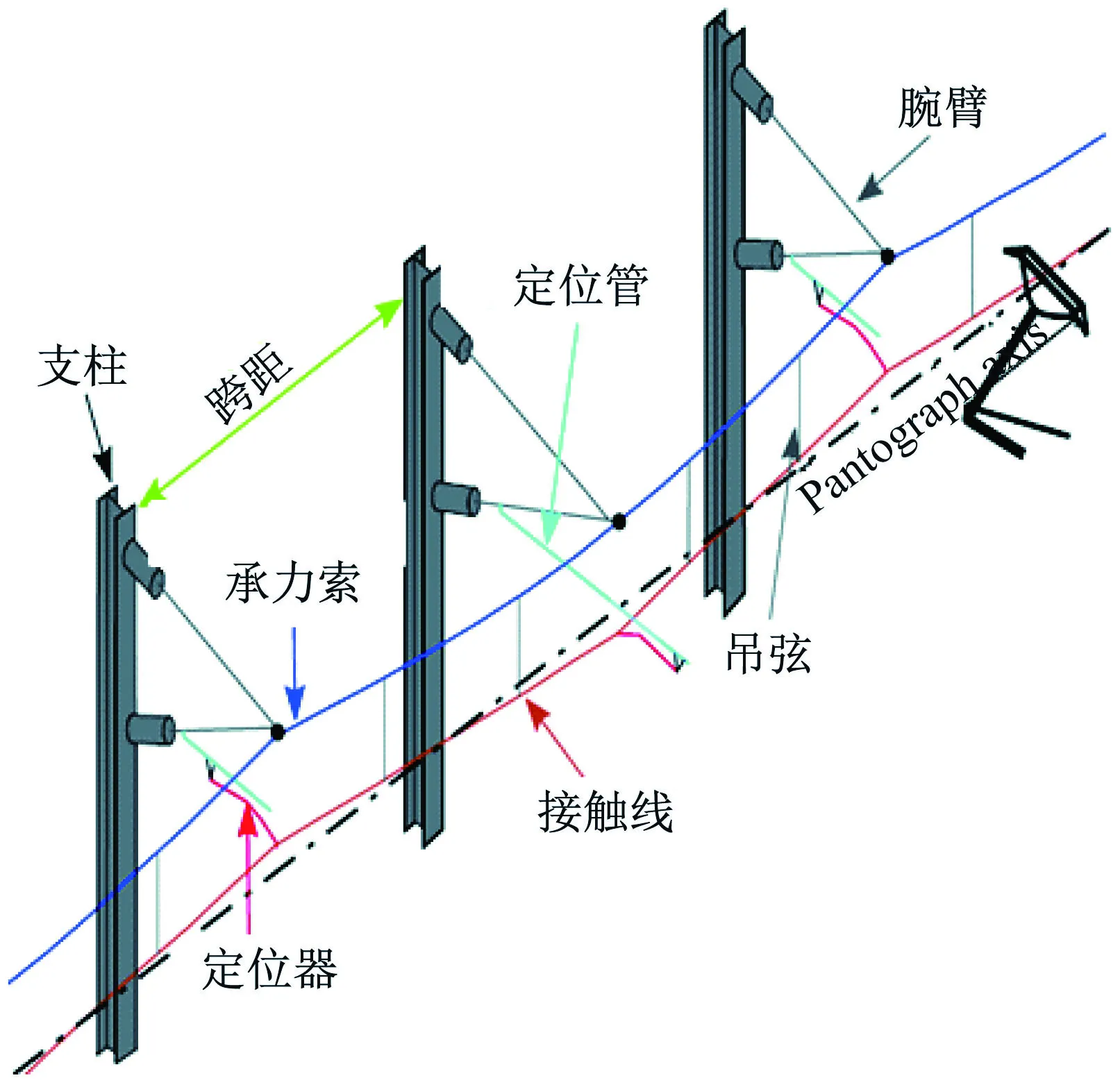
图1 接触网系统示意图
1.1 接触网系统动力学方程
在接触网动力学性能的教学过程中利用势能分析法建立弓网耦合系统动力学方程[14-15]。弓网系统的动能、势能如下:
承力索和接触线位移分别为:
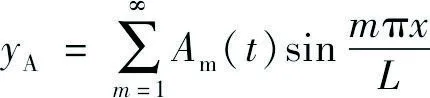
(1)
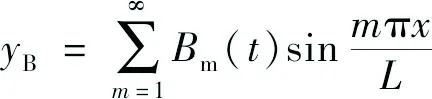
(2)
式中:Am、Bm分别为承力索和接触线的第m阶振动幅值;L为锚段的长度。
承力索和接触线的动能分别为:
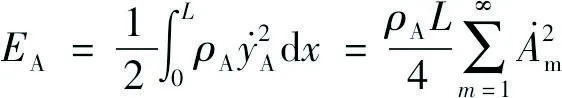
(3)
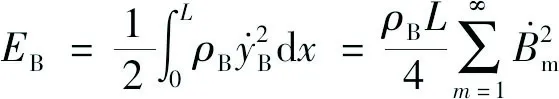
(4)
式中,ρA、ρB分别为承力索和接触线的线密度。
吊弦的动能为:
(5)
式中:MDi为第i个吊弦的质量;P为吊弦的数量。
支撑杆和定位器的动能分别为:
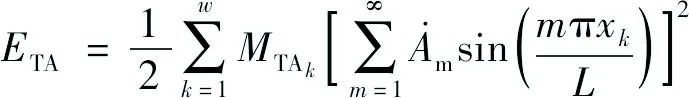
(6)
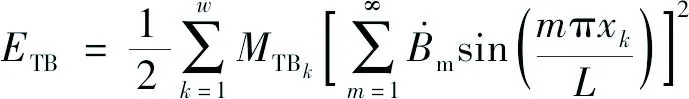
(7)
式中:w为支撑杆(定位器)的数量;MTAk、MTBk为第k个支撑杆和定位器的质量。
受电弓的总动能为:
(8)
式中:M1、M2、M3分别为受电弓3质量块模型中弓头、上臂杆和下臂杆的等效质量;y1、y2、y3分别对应上述质量块的等效位移。
由上述式得到系统总动能为:
E=EA+EB+ED+ETA+ETB+EPAN
(9)
接触线和承力索的抗拉势能为:
(10)
式中,SA、SB分别为承力索和接触线的张力。
接触线和承力索的弯曲势能为:
(11)
式中,EIA、EIB为承力索和接触线的抗弯刚度。
吊悬的弹性势能:
(12)
式中:KDi为第i个吊弦的刚度。
受电弓的弹性势能为:
(13)
式中:K1、K2、K3分别为3质量块受电弓模型中的等效刚度。
弓网间的弹性势能为:
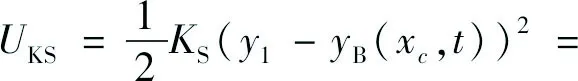
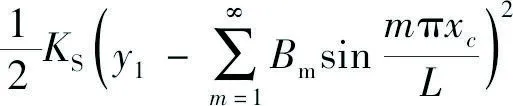
(14)
式中:KS为弓网间的接触刚度;xc为弓网接触位置的横向坐标。
支撑杆和定位器的弹性势能分别为:
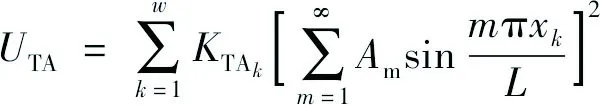
(15)
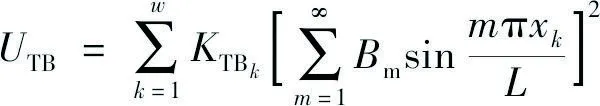
(16)
式中,KTAk、KTBk分别为支撑杆和定位器的刚度。
弓网系统的弹性势能U为:
U=US+UWS+UD+UPAN+
UKS+UTA+UTB
(17)
简化后的承力索n阶振动方程如下:
(18)
简化后的接触线n阶振动方程为:
(19)
由上述理论推导可知,接触网系统动力学方程较为复杂,在教学过程中通过动力学方程判断参数变化对接触网系统动力学性能的影响不够直观。有必要利用有限元方法,直观的展示系统参数变化对接触网动力学性能的影响,践行工程学科倡导的“化抽象为具体”的教学理念。
1.2 接触网系统仿真模型
基于有限元理论、弓网系统动力学理论,采用abaqus软件建立弓网系统仿真模型,如图2所示。受电弓参数取自我国高速铁路普遍采用的SSS400+型受电弓,接触线参数取自京津线高速铁路。仿真模型参数见表1、2。
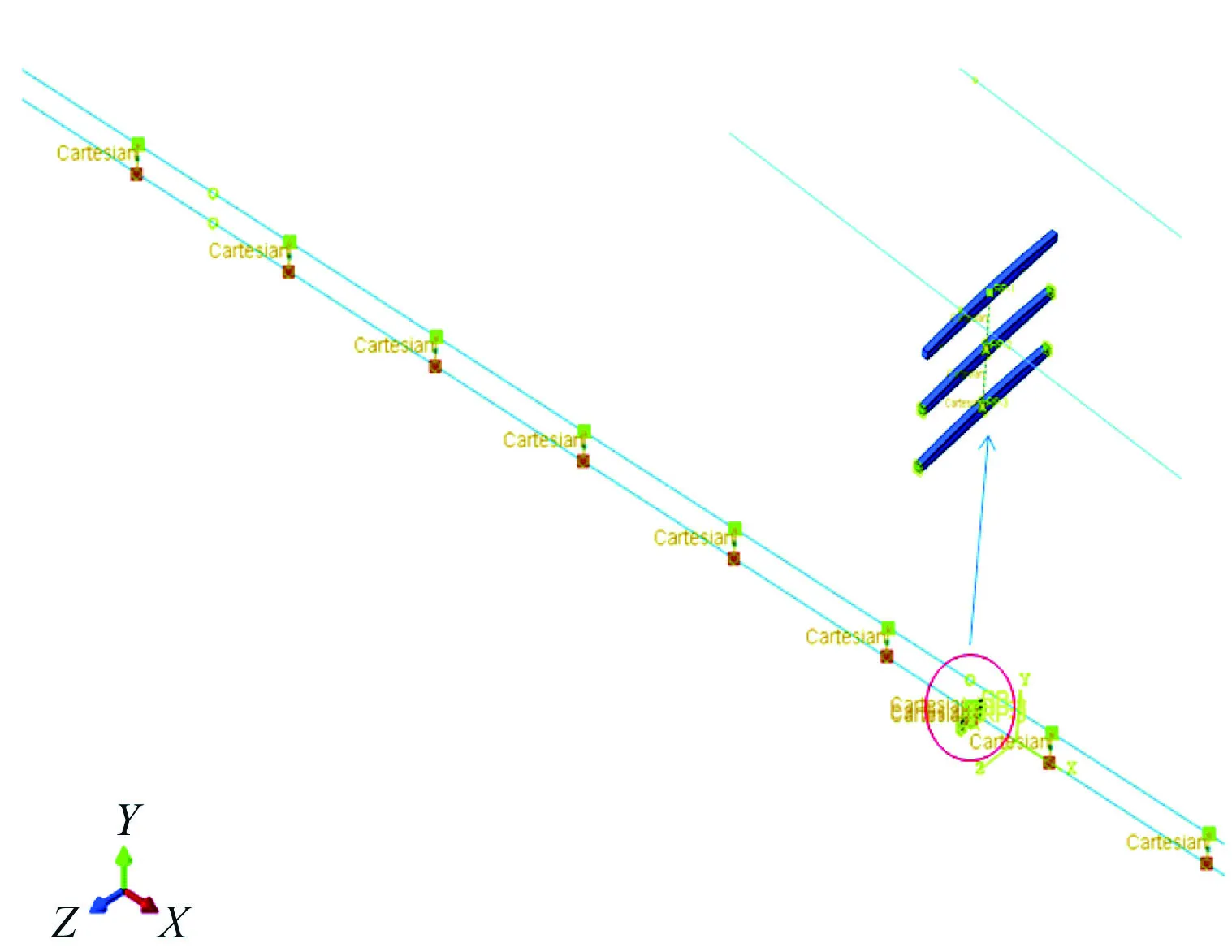
图2 弓网系统模型
表1 受电弓结构参数

参数数值弓头质量,M1/kg6.1上框架质量,M2/kg10.154下臂杆质量,M3/kg10.3弓头刚度,k1/(N·m-1)10400上框架刚度,k2/(N·m-1)10600下臂杆刚度,k3/(N·m-1)0弓头阻尼,c1/(N·s·m-1)10上框架阻,c2/(N·s·m-1)0下臂杆阻,c3/(N·s·m-1)120
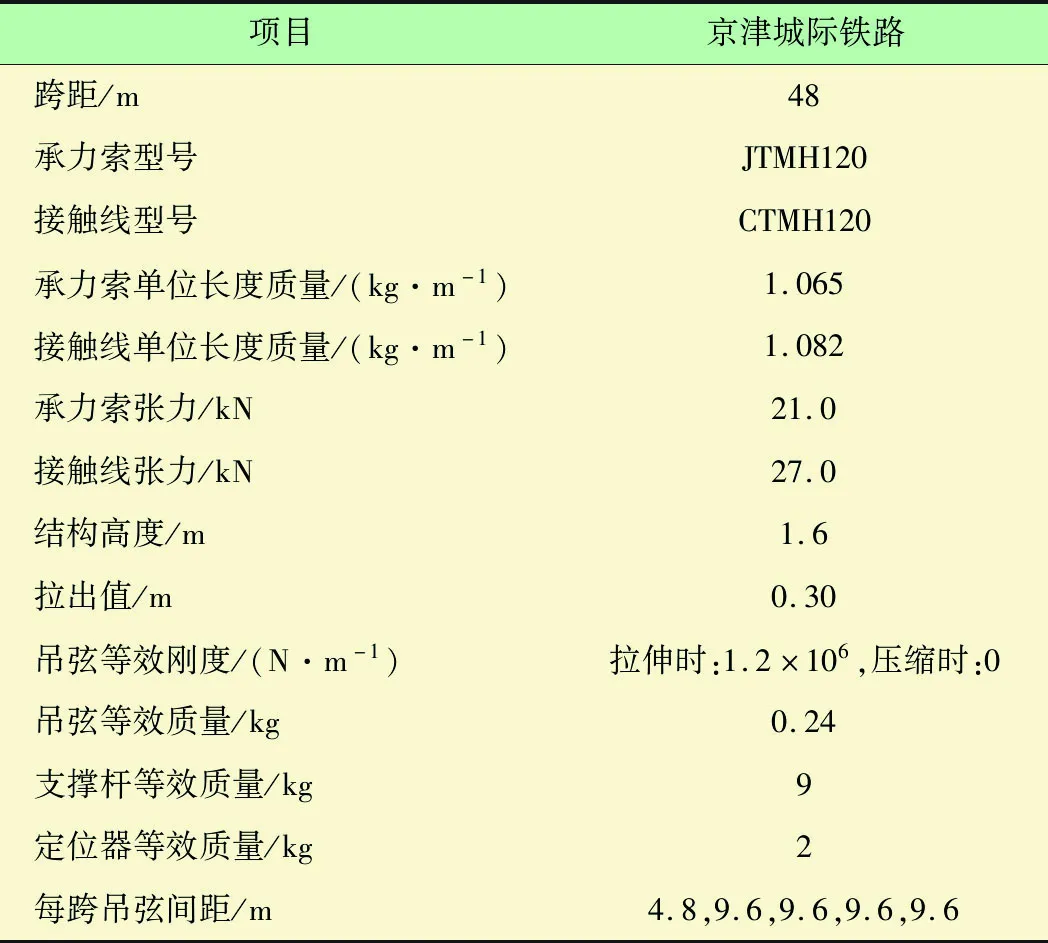
表2 接触网参数
在接触网系统仿真建模过程中,接触线、承力索及吊弦的等效是一项重点难点工作。由于接触网是大跨距的柔性系统,为减小仿真模型体量,较快的获得满足精度要求的计算结果,文中采用梁单元(B31)对接触线和承力索进行离散;实际工况中吊弦由于仅可承受拉力,故采用非线性弹簧对吊弦进行模拟(受压时刚度为0);张力补偿装置等效为接触网两端恒定的集中力;腕臂和定位器等效为一端固定一端附加集中质量的线性弹簧;受电弓采用为弓网动力学分析中应用较多的3质量-弹簧-阻尼模型,建模时第一个质量块的接触表面取自受电弓滑板磨损表面的实际轮廓。受电弓与接触网系统间的相互作用通过添加接触的方式进行耦合(罚函数法);在前处理模块构建弓网系统后,即可生成INP文件。
利用inp文件作为前处理器和求解器之间传递数据的桥梁,通过改变inp文件中关键词(Keyword)对应的参数,模拟不同参数变化(摩擦系数、速度、张力、弓头质量等)对接触网系统动力学性能的影响。采用修改INP文件的方式提交job,可以批量处理job,提高分析效率。限于篇幅仅展示了inp文件中的部分内容:
***
*Mass, elset=Set-92_Inertia-mass-diaoxuan2_
**吊弦质量0.125,
*Element, type=MASS, elset=Set-107_Inertia-
mass-gong_ 81, 1
*Mass, elset=Set-107_Inertia-mass-gong_
**受电弓弓头质量6.1,
*Element, type=MASS, elset=Set-108_
Inertia-mass-shangkuangjia_ 82, 2
*Mass, elset=Set-108_Inertia-mass-shangkuangjia_
**受电弓上框架质量10.154,
*Element, type=MASS, elset=Set-109_
Inertia-mass-xiakuangjia_83, 3
*Mass, elset=Set-109_Inertia-mass-xiakuangjia_
**受电弓下框架质量10.3,
*End Assembly
***
*Connector Behavior, name="ConnSect-Diaoxuan-1,5"
*Connector Elasticity, nonlinear, component=2, independent components=POSITION
2 **1,5吊弦刚度
0., 0.
0., 1.505
1.25e+06, 2.505
***
由于弓网动力学仿真中,接触网及受电弓均会出线较大的几何变形,系统的刚度矩阵将随时间变化,故在仿真过程中采用Newmark积分法对振动微分方程进行求解,最大步长为1 ms。
2 弓网动力学性能仿真实验
弓网间动态接触力是评估弓网系统动力学性能的关键指标。列车的受流质量很大程度上取决于弓网间动态接触力的大小:接触力太小,弓网间容易出现离线电弧;接触压力过大则会导致弓网磨耗加剧,缩短受电弓滑板的更换周期。
2.1 350 km/h时接触网动态响应
将弓网间的摩擦系数设为0.2,弓网间的相对滑动速度设为350 km/h,仿真时间为2.5 s。仿真结果见图3,限于篇幅仅给出了弓网间动态接触力及接触点抬升量随时间的变化曲线。图3中,弓网间动态接触力及接触点抬升量均随时间呈周期性变化,这与接触网刚度随跨度周期性变化相关。由图3可知:弓网间动态接触力在82.6~269.1 N之间波动,符合弓网动态接触力在0~350 N之间变化的要求;受电弓弓头抬升量在31~62 mm之间变化,符合接触点垂向位移范围须小于80 mm的要求;进一步说明,列车以350 km/h运行时,弓网动力学性能符合规范要求[16]。
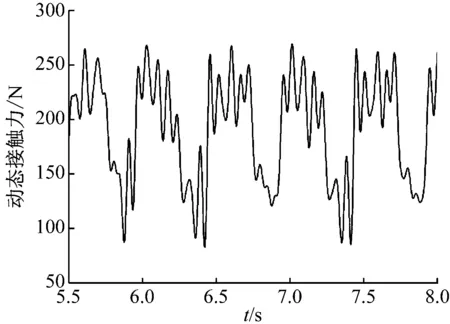
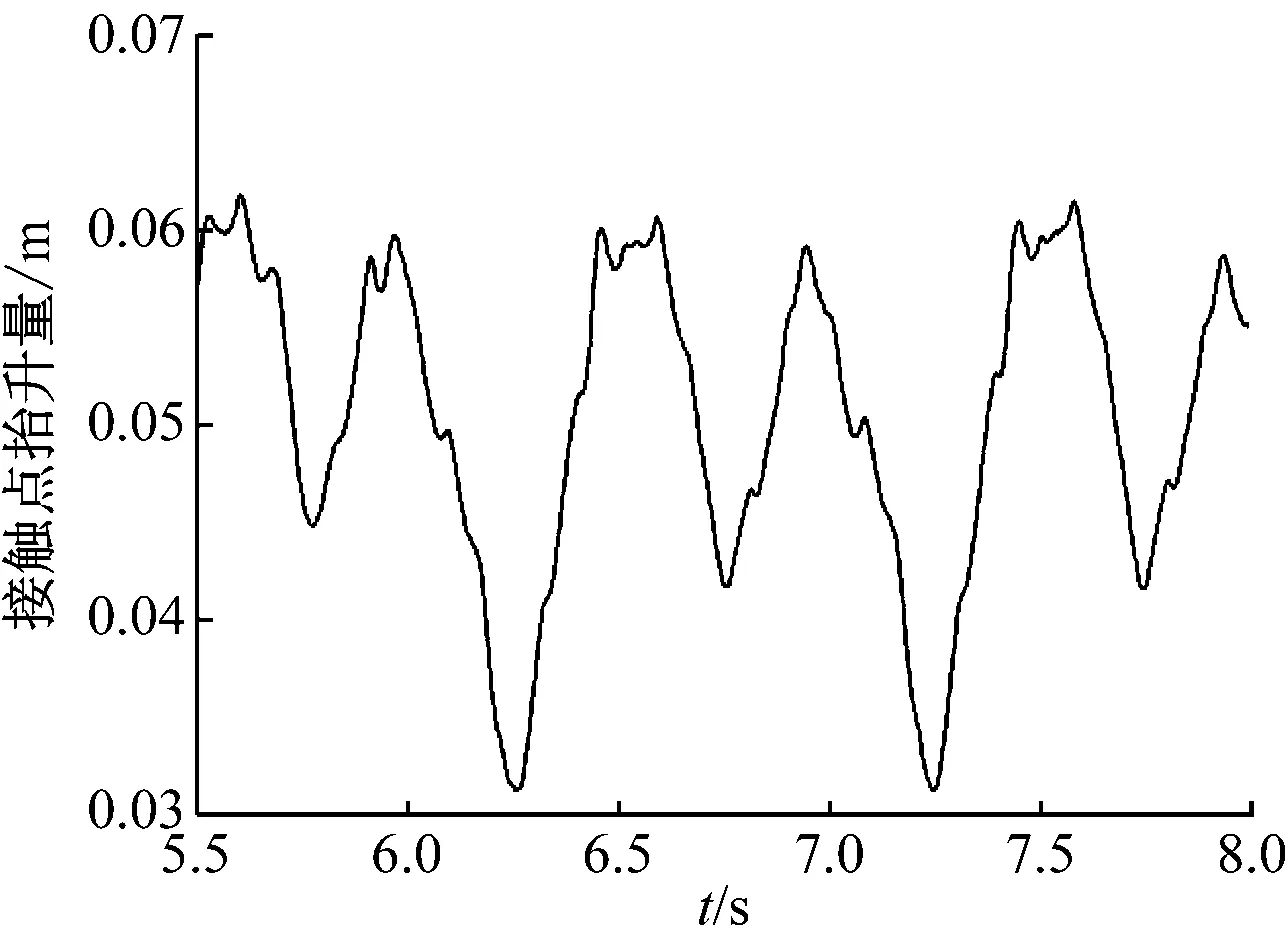
图3 350 km/h时接触网动态响应
2.2 张力变化对弓网间动态接触力的影响
受电弓系统的初始参数保持不变,在INP文件中将接触线张力改为21 kN和33 kN,通过批处理方式提交job,研究接触线张力变化对接触网动力学性能的影响,分析结果见图4。由图4可知:接触线张力为21 kN时,弓网间动态接触力在50.3~280.4 N之间波动;接触线张力为33 kN时,弓网间动态接触力在115.2~253.5 N之间波动;适当提高接触线的张力,弓网间动态接触力的波动范围减小。该仿真结果直观的说明了接触网设计时的一般原则:在一定范围内适当增加接触线的张力,有利于改善弓网间的受流质量。

图4 不同接触线张力时弓网间动态接触力
2.3 弓头质量对动态接触力的影响
接触网系统的参数保持不变,改变受电弓系统的参数。将受电弓弓头的等效质量分别设置为3 kg和9 kg,研究弓头质量变化对接触网动力学性能的影响,分析结果见图5。由图5可知随着弓头质量的增加,弓网间接触力波动范围增大,不利于弓网间的稳定受流。该结论也从侧面说明了当前高速列车受电弓弓头采用轻量化设计的趋势。

图5 不同弓头质量时弓网间动态接触力
3 结 语
本文给出了接触网动力学性能仿真的一般步骤,参考本仿真实验的建模方法,可评估新建或改建线路弓网系统的动力学性能,通过调整诸如接触网张力、密度、吊弦长度、吊弦间距、跨距、定位器拉出值等参数可对既有方案进行优化设计。利用本仿真实验开展教学,一方面可以将复杂的动力学理论直观的展示给学生,提高了教学效果;另一方面也有利于培养了学生运用仿真实验手段解决科研问题的能力。

