基于偏最小二乘回归的疏浚产量预测方法

高 腾，许焕敏

(河海大学 机电工程学院，江苏 常州 213022)

绞吸挖泥船产量决定了工程效益，同时也是评价其性能最为重要的指标之一[1]。预测产量有助于疏浚作业过程中选择最优的作业参数，实现挖泥船的作业优化。由于挖泥船的作业过程由多因素共同作用，产量的影响因素众多，导致对挖泥船产量的预测十分困难。丁树友等[2]研发疏浚作业辅助决策系统并用于疏浚产量的现场寻优，从而提高施工效率;王其松等[3]通过分析大量挖泥船作业反馈的数据，提出将施工经验与施工数据分析相结合，对挖泥船产量进行优化。目前，针对挖泥船产量的优化已经做了大量研究，但产量与工艺参量之间仍缺乏一种可量化的数学关系模型。

因此，本文针对疏浚作业反馈数据，通过Relief权重算法筛选出影响挖泥船产量的主要工艺参量，并在此基础上利用偏最小二乘回归建立产量与主要工艺参量之间的一种可量化的数学模型，为预测挖泥船的产量提供一种方法，对疏浚作业优化具有重要的现实意义。

1 产量主要工艺参量筛选

1.1 绞吸挖泥船影响参量提取

根据文献[3]可知,挖泥船的产量可由下式表示：

W=QC=πr2vC

(1)

(2)

式中：W为挖泥船的产量(m3s)；Q为泥浆流量(m3s)；C为泥浆浓度，以质量百分比表示(%)；r为挖泥船排泥管的半径(m)；v为泥浆流速(ms)；ρs为泥浆密度(kgm3);ρw为水的密度(kgm3)；ρn为泥沙的干密度(kgm3);ε为泥沙孔隙率。

根据式(1)、(2)可得：

(3)

根据式(3)可得，挖泥船的产量与排泥管半径、泥浆流速、泥浆密度、泥沙干密度、泥沙孔隙率有关。其中除去排泥管半径、泥沙干密度及泥沙孔隙率这些不可控的因素外，泥浆流速、密度与泥泵功率和绞刀性能密切相关。因此，总结影响挖泥船作业产量的工艺参量有：绞刀转速(rmin)、泵轴转速(rmin)、横移速度(ms)、管路平均浓度(%)、管路流速(ms)、出口流速(ms)、绞刀切泥厚度(m)、绞刀前进距离(m)和台车行程(m)，共9个参量。

1.2 实时数据标准化处理

基于“天狮号”绞吸挖泥船实时反馈的数据，随机提取100组上述工艺参量的数据，见表1。

表1 产量与各工艺参量数据

由于所提取的产量及各工艺参量的数值不在同一个数量级，因此，为消除不同量纲带来的影响，首先需要对所提取的数据进行标准化处理。标准化变换如下：

(4)

1.3 参量筛选的Relief算法实现

产量的影响因素众多，提取对产量影响较大的参量对降低挖泥船作业复杂度具有重要意义。对原始数据进行标准化处理后，利用Relief权重算法[4]，对工艺参量进行筛选。Relief算法由Kira提出，是目前最为有效的特征选择方法之一，该算法依据特征和类别的相关性赋予特征不同的权重，权重小于某个阈值的特征将被剔除[5]，以此作为特征筛选的理由。Relief算法流程如图1所示。

算法实现过程使用MATLAB实现。将表1的数据随机划分为两类，每一类各50组数据，不设置权重的阈值。按照每个参量权重的大小进行排序，提取权重较大的工艺参量。由于两类数据是随机划分的，为避免程序运行导致的试验误差，将程序运行20次，取平均值作为最终计算结果。如图2所示。其中垂直矩形越高，则表示该参量的权重越大。

根据图2，将各参量按权重大小进行排序，从大到小依次为：管路平均浓度、管路流速、绞刀前进距离、绞刀切泥厚度、绞刀转速、横移速度、台车行程、出口流速、泵轴转速。

由权重大小可知，大部分的参量权重都高于0.1，所以将权重低于0.1的剔除。因此，保留的工艺参量有：管路平均浓度、管路流速、绞刀前近距离、绞刀切泥厚度、绞刀转速、横移速度。根据文献[6]，挖泥船作业产量主要与泥泵特性和管路特性有关,所以提取出的主要工艺参量符合疏浚工程中的实际应用。

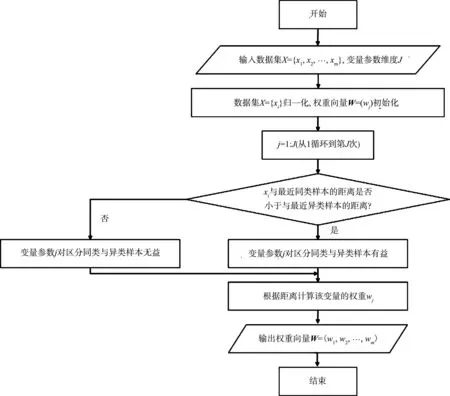
图1 Relief算法流程

图2 参量权重

2 偏最小二乘回归分析

2.1 偏最小二乘回归理论分析

偏最小二乘回归是一种多元统计数据分析方法，它的研究内容主要是多因变量与多自变量之间的回归建模，特别是当自变量内部存在着多重相关性时，而疏浚作业中各工艺参量之间相互影响，关系复杂，因此，采用偏最小二乘回归进行建模则会更加有效。

1)从标准化自变量矩阵中提取第一个主成分t1，其中w1为标准化自变量矩阵的第一主轴,且

(5)

t1=E0w1

(6)

E0=t1pT1+E1

(7)

(8)

F0=t1rT1+F1

(9)

式中：E1为标准化自变量矩阵的残差矩阵；p1为E0在第一主成分上的回归系数；F1为标准化因变量矩阵的残差矩阵；r1为F0在第一主成分上的回归系数。

2)以E1取代E0、F1取代F0，用同样的方法重复步骤1)，有：

(10)

t2=E1w2

(11)

E1=t2pT2+E2

(12)

(13)

F1=t2rT2+F2

(14)

以此类推，从步骤2)开始，可以使用交叉有效性确定偏最小二乘回归所提取的成分个数。

3)确定所提取的成分t1,t2,…,tm后，进行回归分析。首先实施F0关于t1,t2,…,tm的回归：

F0=r1t1+r2t2+…+rmtm

(15)

由于所提取的成分th(h=1,2,…,m)均为E0的线性组合，因此

(16)

F0=r1E0w*1+…+rmE0w*m=E0(r1w*1+…+rmw*m)

(17)

y*=β1x*1+β2x*2+…+βpx*p

(18)

式中：β1、β2、…、βp为标准化数据的系数。

最后，通过数据标准化的逆过程，可得到因变量y关于自变量xj的回归方程为

y=α0+α1x1+…+αpxp

(19)

式中：α0、α1、…、αp为回归方程的回归系数。

2.2 交叉有效性分析

偏最小二乘回归一般来说不需要采用所有的成分进行建模，选择成分的个数可通过增加一个成分，判断新增的成分能否对模型的预测精度有明显的提升来确定。

记yi为原始数据，t1,t2,…,th是偏最小二乘回归分析中提取的所有成分，yh(-i)表示在建模过程中，除去第i个样本点后，用t1,t2,…,th这些成分进行建模，再根据此模型计算第i个样本的预测值；yh(i)表示在建模过程中，选取所有的样本点并使用成分t1,t2,…,th进行建模后，根据此建模模型预测的第i个样本点的拟合值。PRESSh为因变量的预测误差平方和，SSh表示误差平方和，Q2h定义为交叉有效性，计算公式为：

(20)

(21)

(22)

一般情况下认为，当Q2h≥0.097 5时，表明增加的成分对于改善回归模型的精度有着显著的作用，因此可以继续增加偏最小二乘回归的成分，直至当Q2h< 0.097 5时，可不再增加回归模型的成分，这时提取的成分个数即为偏最小二乘回归的最佳成分个数[7]。

3 实例分析

以“天狮号”绞吸挖泥船实时反馈数据为例，共1 000组作为试验数据。基于主要工艺参量筛选后的结果，根据偏最小二乘回归原理，建立如下的数学模型：

y=1.838 8+0.014 6x1+0.010 8x2-0.001 6x3-

0.106 4x4-0.008 7x5-0.075 7x6

(23)

式中：y为产量(m3s);x1为绞刀转速(rmin)；x2为横移速度(ms)；x3为管路平均浓度(%)；x4为管路流速(ms)；x5为绞刀切泥厚度(m)；x6为绞刀前进距离(m)。

为避免偶然误差，从1 000组数据中随机选取50组作为试验样本，比较预测产量与实际产量，如图3所示。

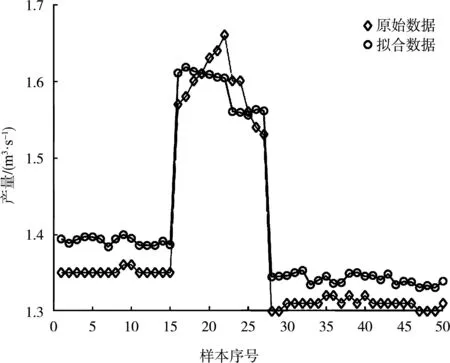
图3 预测产量与实际产量比较

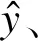
4 结论

1)为了筛选出影响产量的主要工艺参量，降低作业复杂度。本文利用Relief权重算法，根据各工艺参量的权重大小提取出权重较大的主要工艺参量作为数学模型的自变量。

2)通过偏最小二乘回归分析建立产量与主要工艺参量之间的数学模型，并对模型的拟合效果进行分析，该方法建立的数学模型能够较好地对产量进行预测。

3)本文中利用偏最小二乘回归建立的产量与主要工艺参量之间的数学模型，不仅可用于对挖泥船的产量进行预测，同时也能选择最优作业参数，实现挖泥船的作业优化，从而提高作业效率。