高一物理中渗透极限方法教育探讨

(广西壮族自治区南宁市第三中学,广西 南宁 530201)

科学思维是学生在学习和运用物理知识和方法过程中必备的能力,也是核心素养的重要方面,教师应有意识地在教学中培养学生的科学思维能力。人教版教材中多次展现极限方法的运用,其目的是让学生通过多次接触,逐步领悟、掌握；微元法是极限方法的基本应用,运用微元法可以快速解决较复杂的高中物理问题,只有对极限方法有了一定的理解,才能理解和应用微元法。科学思维的形成需要学生在学习过程中不断体会和领悟,这就要求教师在教学中应有意识、有计划地进行渗透。

依据皮亚杰认知发展理论,高一学生处在“形式运算阶段”,多数学生具备一定的抽象思维能力,但仍较薄弱。笔者按照“初步体会—初步感受应用—初步尝试应用—再次感悟”的程序，在高一逐步进行渗透,使学生对极限方法经历螺旋式上升的理解过程。

1 逐步体会

高中物理首次运用极限方法的是瞬时速度的概念,在瞬时速度的教学中,让学生了解极限方法,初步体会即可。

师：我们知道平均速度是描述一段时间内的运动快慢,如果想知道刘翔在经过终点那一刻的速度是多大,该怎么办呢?

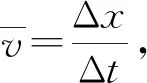
图1

生：第3张，时间间隔是0.02s,更精确。

通过讨论,教师给出瞬时速度的定义,并明确向学生指出：时间间隔Δt非常非常小,无限接近于0,这在技术上很难实现,但我们可以运用极限思维在头脑中“实现”,因此极限思维是处理物理问题的一种重要思维方法。

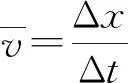
2 感受应用

学习过瞬时速度后,学生初步了解了极限思维,但尚未明了如何应用极限思维解决物理问题。必修一2.3节中通过“无限分割”v-t图像得出“面积代表位移”结论,又运用了极限方法，本节是使学生感受利用极限思维解决问题的重要契机。

师生共同学习了教材“思考与讨论”的内容后，教师提问：如何在小车的v-t图像上运用极限方法？

生：在v-t图像中每一个小矩形代表一段时间内的位移,这些矩形“面积”之和就是物体运动的位移(如图2)。

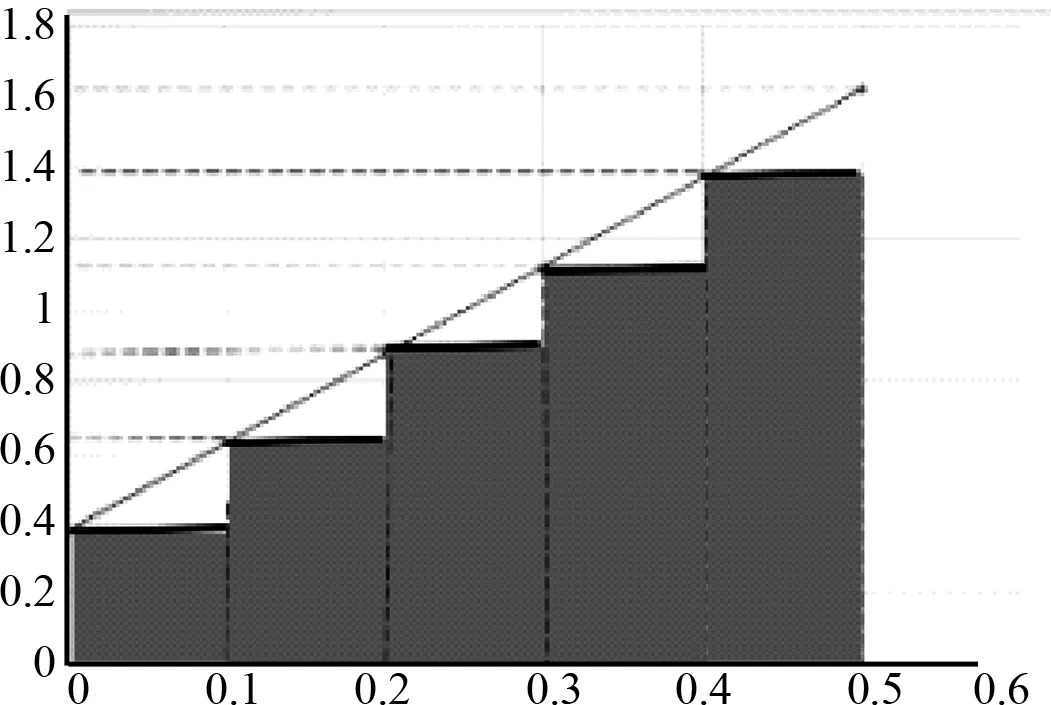
图2

师：如果时间间隔取的是0.04s,还是采用上述方法估算位移,我们又该如何在v-t图像中体现呢?如果时间间隔取得更小,比如取0.02s、0.01s，甚至更小呢?

师生共同探究：时间间隔越小,相当于把时间均分的份数越多,借助GeoGebra分析，把时间分割成多份(图3为分割成20份、图4为分割成100份),我们发现时间被分割的份数越多,小矩形越多,小矩形“面积”之和就越接近于图线与坐标轴围成的“面积”,我们可以想象：当时间被分割成无限多份,这些无限多个小矩形“面积”之和就等于梯形的“面积”。极限是一种重要的思想方法,之前由平均速度引出瞬时速度时我们也用到了极限方法。

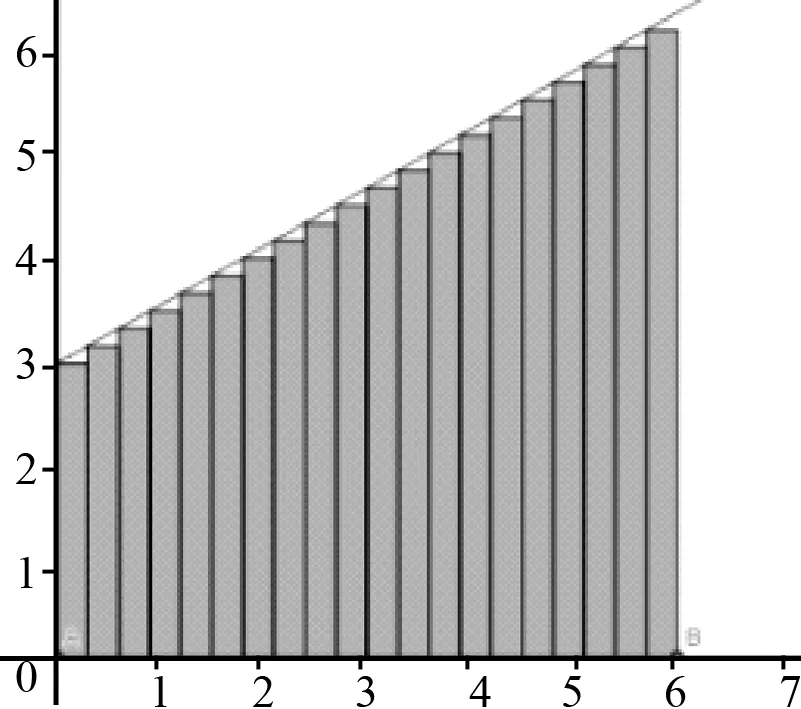
图3

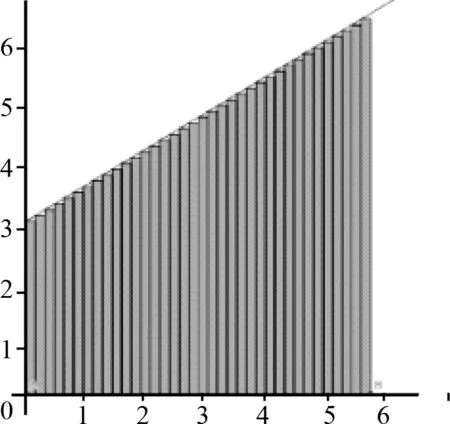
图4

在教学中,通过“无限分割”时间,获取时间微元Δt,在Δt时间内把“变速”当“匀速”,再对所有Δt内的匀速直线运动的位移求和，即为匀变速直线运动的总位移。微元法是极限方法的基本应用之一,在上述教学中已有体现,但是不宜要求学生完全掌握,只要求学生初步感受利用极限方法解决物理问题。另外在新课教学中借助GeoGebra软件进行动态演示,可以让学生经历从感性到理性的认知过程,更有利于学生接受极限方法。

3 尝试应用

3.1 向心加速度表达式的推导

必修2第五章第5节“做一做”栏目从一般性的结论出发,利用极限方法从理论上研究向心加速度的方向和表达式。由于向心加速度表达式的推导过程比较抽象,很多教师在教学中回避了推导过程,直接把公式告知学生。笔者认为：学生经历了几次极限方法的渗透和感悟,已具备在教师的帮助下尝试使用极限方法解决问题的能力,因此本节课是学生尝试使用极限方法的良机。

(1) 向心加速度的方向

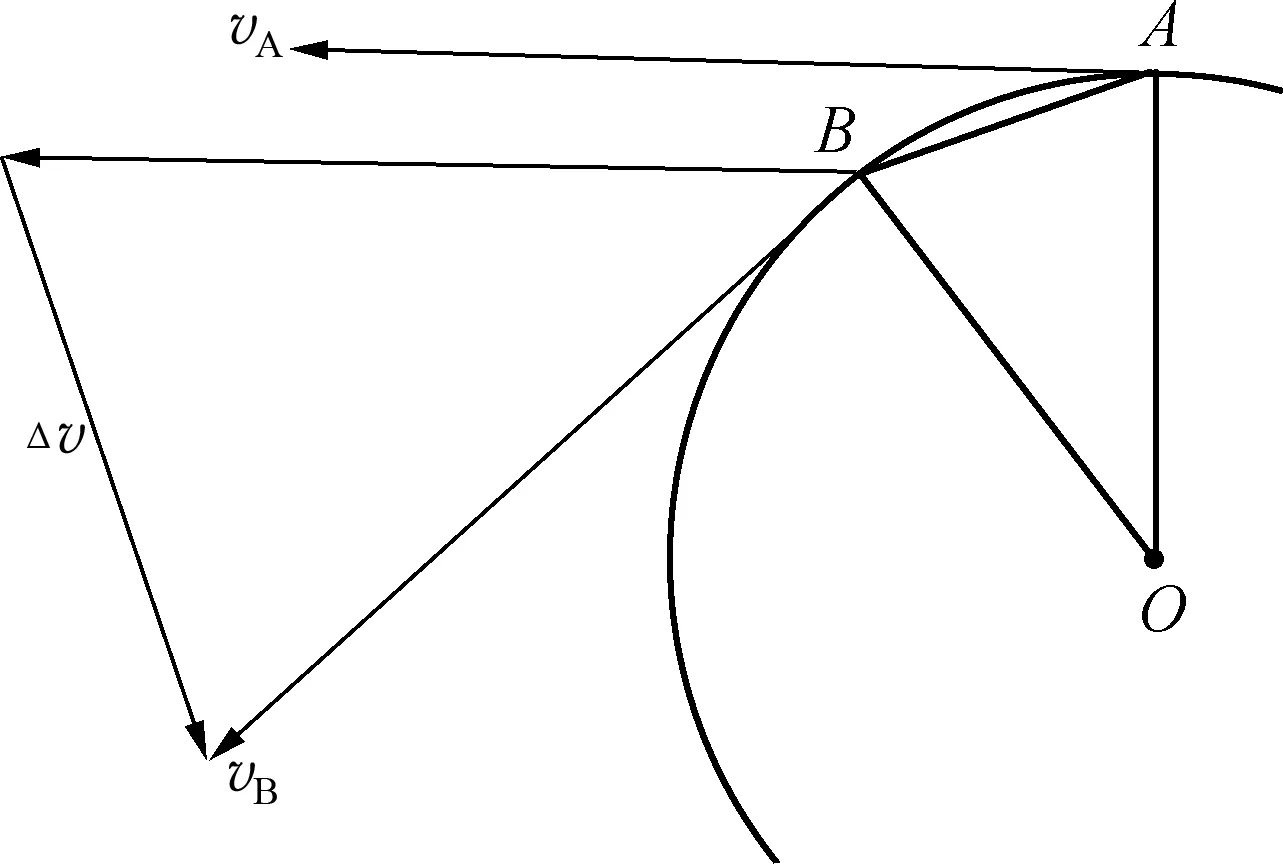
图5

图6

(2) 向心加速度表达式

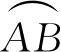
3.2 开普勒第二定律的证明

开普勒第二定律也叫面积定律,即：行星与太阳的连线在相等的时间内扫过相等的面积。根据开普勒第二定律可推知：行星在远日点速度小,在近日点速度大。

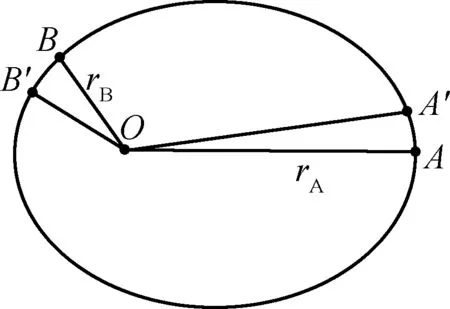
图7

3.3 重力做的功

如图8所示，小球A从同一高度按不同的路径下降到另一高度,对于按(1)、(2)方式下降,学生利用公式W=Fscosθ，能快速计算出重力做功为mgh。若小球按任意曲线下降,该如何求解呢?教师引导学生：

图8

(1) 在求解匀变速直线运动的位移时,我们是把物体的运动分解成很多段“匀速运动”,通过类比,小球下降的路径能不能也分成很多段?

(2) 当分的段数越多,每一间隔就越接近一段倾斜的线段,物体通过s1这段位移时,重力做的功是多少?

答：ΔW1=mgs1cosθ=mgΔh1。

(3) 物体通过整个路径,重力做的功是多少?

答：W=W1+W2+…=mg(Δh1+Δh2+…)=mgh。

证明过程利用极限方法来“化曲为直”,使复杂的物理问题转变成简单的问题。先无限分割,对一微元过程进行分析,找出规律,再求和,展现了微元法的基本应用步骤。

4 再次感悟

关于“弹性势能的表达式”,课标明确提出“着重体会探究过程,领悟研究方法”。功与能有密切的关系,可通过弹力做功去

研究弹性势能。弹簧的形变量越大,弹力越大,弹力做功属于变力做功,如何求出弹簧被拉长x的过程中弹力做的功?教师引导学生回忆求匀变速直线运动位移的方法：把物体的运动分割成很多份,每一小份速度的变化很小,可以近似认为每一份是匀速运动,求出每一小份的位移后再求和。对于弹力做功,可用同样的方法来处理：把弹簧被拉长的过程分解成很多段,每一小段的长度为Δx1,Δx2,Δx3,…每一小段的拉力认为是不变的,即每一小段的弹力分别为F1,F2,F3,…整个过程弹力做功为F1Δx1+F2Δx2+F3Δx3+…类比匀变速直线运动v-t图线下的“面积”表示位移,同样可以借助F-x图像求出弹力所做的功，得到弹性势能的表达式。

5 结语

在人教版教材中,极限方法在概念的定义、结论的推导中多次出现,但没有直接说明,这就要求教师从更宽的视角研读教材,体会教材中蕴含的科学思维方法,并将之显性化。科学思维不是一朝一夕就可以培养的,只要教师在教学中不断渗透,学生自有浸润、感悟、理解,为物理学习打下坚实的基础。