天津滨海新区土层邓肯-张模型参数研究

徐小明，常高奇

（中交第一航务工程勘察设计院有限公司，天津 300222）

引 言

京津冀地区粘性土特别是软土具有承载力低、压缩性高、渗透性低等特点，属于典型的第四纪全新世滨海沉积，研究土体受到荷载作用后的最终破坏状态便尤为重要，因此大部分情况下可以在不考虑时间对土的应力-应变和强度的影响，研究土的受力变形发展。为便于研究天津滨海新区地层土体的变形特性，进行土的非线性应力变形计算，需采用研究形式较易于推广、涉及参数可以通过试验获得、能够较好的反应土体变形的本构模型。基于广义胡克定律的线弹性理论形式简单、参数少、物理意义明确，在许多工程领域中广泛应用，但由于天津滨海新区地层情况以及工程建设对土体变形的要求较大，因此采用非线性弹性理论对土的应力应变关系进行研究。1963年，康纳通过双曲线拟合出土的三轴试验的应力应变关系曲线，之后邓肯等人在此基础上提出了增量弹性模型，即邓肯-张（Duncan-Chang）模型。孙谷雨对南京地区土样在冻结状态下进行三轴固结排水（CD）试验，并对进行邓肯-张模型参数进行研究分析[1]；张云等通过大量土样的三轴固结排水（CD）中得到上海各主要土层的邓肯-张模型参数，并进行线性分析，得出其模型参数的取值特点以及变化规律[2]；罗刚等对邓肯-张非线性弹性模型进行了一定的改进[3]。该模型可以很好的反映土应力-应变关系的非线性变形特性，其参数可以通过室内三轴试验获得，本文将在前人学者的研究基础上，对于天津滨海新区土层的邓肯-张模型参数进行理论计算，并分析研究。以期望可以很好地反映天津滨海新区地层的变形特性。

本文以天津滨海新区地层为研究对象，根据室内土工试验结果以及该地区地层情况，选取具有代表性地层的土样进行室内三轴固结排水（CD）试验，获得不同地层的邓肯-张模型参数，并进行分析探讨，得出该地区邓肯-张模型参数规律，为今后的工程建设涉及地层变形特性研究提供借鉴。

1 邓肯-张模型参数的确定

康纳提出的利用双曲线来拟合土体常规三轴试验的偏应力与轴应变的关系曲线，即：

将式（1）变形后可得：

绘制以1ε为横坐标，以为纵坐标的散点图，若式（2）看作是以1ε为自变量，以为因变量的一次函数，可将这些散点近似拟合成为线性关系。其中a为直线的截距，b为直线的斜率。

在常规三轴试验过程中，2σ、3σ为定值，即dσ2=dσ3=0，则土样的切线模量可表示为：

在式（3）中，当ε1→0+时，土样的起始变形模量；在式（1）中，当ε1→+∞时，土样的极限偏差应力值。即在截距a可看作是土样在三轴试验中的起始切线模量Ei的倒数，斜率b可看作是土样在三轴试验中的极限偏差应力(σ1-σ3)ult的倒数。

对实际的三轴试验应力应变曲线而言，ε1并不能无限大，因此(σ1-σ3)ult的值难以确定，为解决这一难题，引入破坏比Rf。当该曲线有峰值时，则土的破坏偏差应力(σ1-σ3)f=(σ1-σ3)峰值；当曲线没有峰值时，可根据一定的应变值（通常取ε1=15%）对应的偏差应力为(σ1-σ3)f。此时破坏比公式为：

根据Janbu经验公式：

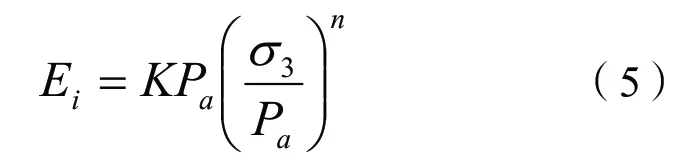
以及摩尔-库伦强度准则，则有：

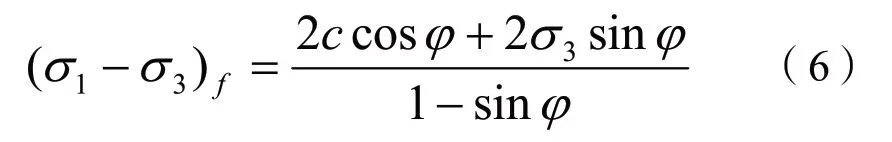
将式（2）、（4）、（5）、（6）带入式（3）得出邓肯-张模型土的切线变形模量表达式：

式中：Pa为大气压，一般取Pa=101.3 kPa；σ1-σ3为主应力差（kPa）；φ为土的内摩擦角（°）；c为土的内聚力（kPa）；Rf为破坏比，无量纲；(σ1-σ3)f为土样破坏时的偏差应力值，（kPa）；(σ1-σ3)ult为土样应变很大时的极限偏差应力值，（kPa）；K、n为邓肯-张模型中材料参数，无量纲。

邓肯-张模型土的体积变形模量B，其大小可通过三轴试验结果确定，计算公式为：

式中：(σ1-σ3)70%和(εV)70%分别表示当(σ1-σ3)达到(σ1-σ3)f的70%时，相应的土样的偏差应力和体应变。由此可知，围压一旦确定，体积变形模量B就是定值，因此，体积变形模量B是与围压有关的常数，邓肯-张模型中土的体积变形模量B表达式为：

由式（8）、（9）可知，邓肯-张模型中的参数共7个，分别是c、φ、Rf、K、Kb、n、m。

以天津滨海新区粉质粘土层土样的三轴固结排水试验为例，分别计算其邓肯-张模型参数。

1.1 参数c、φ的确定

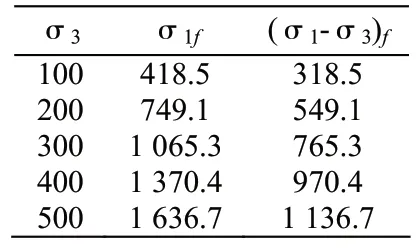
表1 偏差应力计算

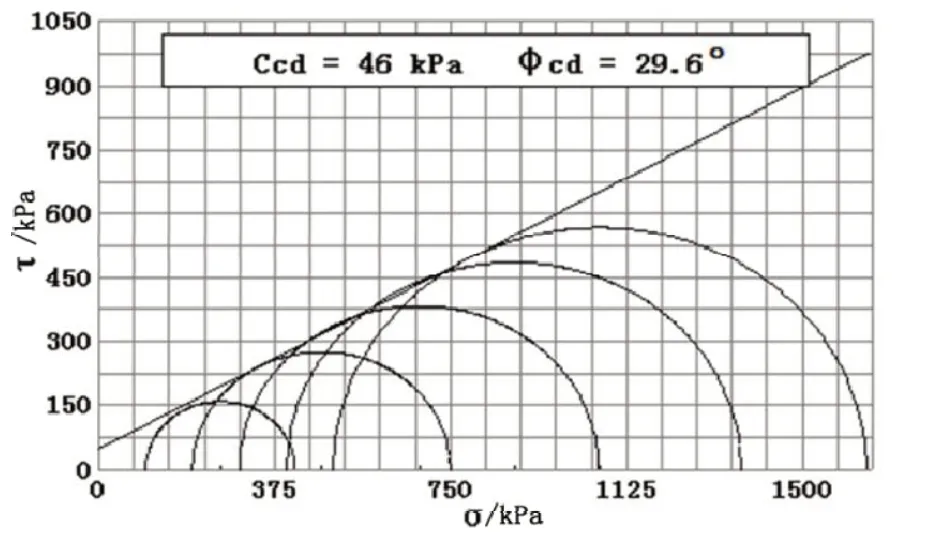
图1 应力差强度包线

以第③层粉质粘土为例，取该土样(σ1-σ3)f为轴向应变在15%时对应的偏差应力，表1所示为不同围压下的土样破坏时偏差应力计算，其中σ1f为土样破坏时的轴应力值。图1为该土样的应力差强度包线，则该土样的c=46 kPa、φ=29.6°。

1.2 参数Rf的确定

为便于确定参数Rf，需引入参数S，定义参数S为应力水平，其计算公式为：

在用一次函数拟合以1ε为横坐标，以为纵坐标的散点图时，其相关系数往往小于1，这是因为应力水平偏高或者偏低都会发生试验点偏离直线的情况，因此根据邓肯等关于计算直线的截距a以及斜率b的计算方法，分别计算当S=70%、S=90%时，土样在不同围压下对应的1ε、的值。在绘制直线时，使直线通过应力水平S=70%以及S=90%的点。绘制线性关系曲线，如图2所示，由图中各直线的截距和斜率，可知土样在不同围压下系数a、b的值，然后可计算出对应的Ei、Rf的值，计算结果如表2、表3所示。

图2 ε1 /(σ 1 - σ 3)与ε1关系趋势线

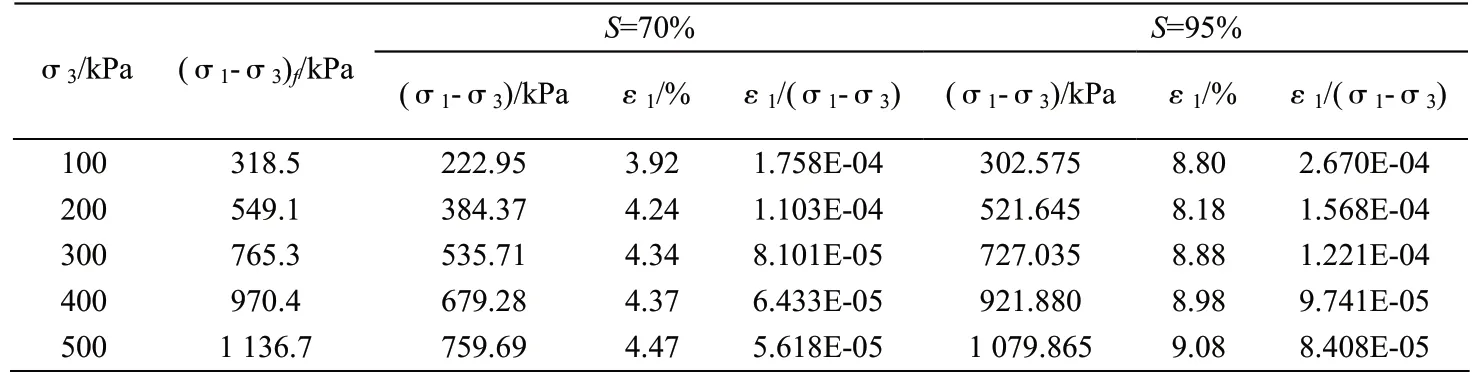
表2 不同围压下的 (σ 1- σ 3)与ε1计算

表3 参数Ei和Rf计算

1.3 参数K、n的确定

表4 不同围压下y和x计算

图3 y和x关系趋势线

若以x为自变量，y为因变量，则式（11）可看作是x～y线性关系的直线解析式，该直线的截距为lgK，斜率为n。分别计算土样在不同围压下x、y的值，计算结果如表4所示，绘制x～y散点图，进行线性拟合，拟合结果如图3所示，因此参数K=118.74、n=0.642。

1.4 参数Kb、m的确定

若以y为自变量，z为因变量，则公式（12）可看作是z～y线性关系的直线解析式，该直线的截距为lgKb，斜率为m。分别计算土样在不同围压下z、y的值，计算结果如表5所示，根据计算结果绘制z～y散点图，进行线性拟合，拟合结果如图4所示，因此参数K=57.29、m=0.532。

表5 不同围压下B和z计算

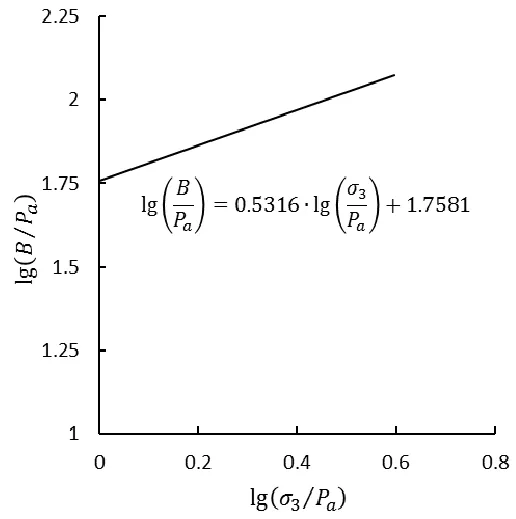
图4 参数B和z关系趋势线

综合可知该土样的邓肯-张模型的7个参数，结果如表6所示。

表6 土样邓肯-张模型参数

2 邓肯-张模型参数的分析

为对各主要土层的邓肯-张模型参数进行分析，根据选取的各土层土样的三轴固结排水试验结果，分别计算其邓肯-张模型参数进行统计，同一地层的各参数则选取其平均值，其结果如表7所示。

图5为K与φ的关系曲线，随着φ值的不断增加，K也相应增大，两者之间的关系可以拟合为K=4.1291e0.109φ，相关系数R2=0.8729，具有较强的相关性。K与c之间并没有明显的相关关系。

图6为Kb与φ的关系曲线，随着φ值的不断增加，Kb也相应增大，两者之间的关系可以拟合为Kb=0.5374e0.1442φ，相关系数R2=0.887，具有较强的相关性。Kb与c之间并没有明显的相关关系。

表7 天津滨海新区各主要土层邓肯-张模型参数

图5 参数K与φ的关系曲线

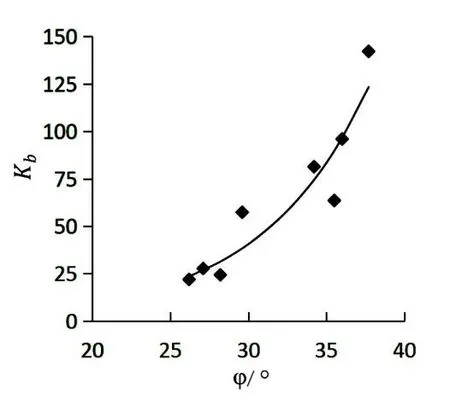
图6 参数Kb与φ的关系曲线

参数Rf、n、m与c、φ值之间并没有明显的相关性。Rf分布在0.644～0.765范围之间，平均值为0.698，标准差为0.040，变异系数为5.8%，变异系数小于15%，无需剔除数据；n分布在0.471～0.761范围之间，平均值为0.630，标准差为0.011，变异系数为16.7%，变异系数大于15%，剔除偏离平均值最大的数后，其平均值为0.652，标准差为0.091，变异系数为14.0%，变异系数小于15%，无需再剔除数据；m分布在0.532～0.829之间，平均值为0.623，标准差为0.092，变异系数为14.7%，接近15%，剔除偏离平均值最大的数后，其平均值为0.594，标准差为0.052，变异系数为8.8%，无需再剔除数据。

3 结 论

通过对天津滨海新区主要地层土样的三轴固结排水剪试验数据计算，分析天津滨海新区的邓肯-张模型参数的变化规律，并得出以下结论：

1）随着φ值的不断增加，K也相应增大，近似指数关系，相关系数为0.8729，具有较好的相关性；

2）随着φ值的不断增加，Kb也相应增大，近似指数关系，相关系数为0.887，具有较好的相关性；

3）参数Rf、n、m与c、φ值之间并没有明显的相关性，其离散度从大到小依次为m、n、Rf。

4）参数Rf取值范围为0.644～0.765，一般可取平均值0.698；参数n取值范围为0.471～0.761，一般可取平均值0.652；参数m取值范围为0.532～0.829，一般可取平均值0.594。