新型冠状病毒肺炎早期时空传播特征分析*
王聪 严洁 王旭 李敏
1)(四川警察学院计算机科学与技术系,泸州 646000)
2)(四川警察学院,四川警事科学研究院,成都 610200)
3)(四川警察学院道路交通管理系,泸州 646000)
4)(四川师范大学影视与传媒学院,成都 610068)
5)(四川师范大学计算机科学学院,成都 610068)
通过最新公布的流行病学数据估计了易感者-感染者模型参数,结合百度迁徙数据和公开新闻报道,刻画了疫情前期武汉市人口流动特征,并代入提出的支持人口流动特征的时域差分方程模型进行动力学模拟,得到一些推论: 1)未受干预时传染率在一般环境下以95%的置信度位于区间[0.2068,0.2073],拟合优度达到0.999;对应地,基本传染数R0位于区间[2.5510,2.6555];极限环境个案推演的传染率极值为0.2862,相应的R0极值为3.1465;2)百度迁徙规模指数与铁路发送旅客人数的Pearson相关系数达到0.9108,有理由作为人口流动的有效估计;3)提出的模型可有效推演疫情蔓延至外省乃至全国的日期,其中41.38%的预测误差≤ 1 d,79.31%的预测误差 ≤ 3 d,96.55%预测误差 ≤ 5 d,总体平均误差约为 2.14 d.
1 引 言
2020年伊始,新型冠状病毒肺炎(COVID-19)疫情猝然爆发.临近春节,疫情在春运因素的叠加下从九省通衢的武汉三镇向祖国大地迅速蔓延.目前国内疫情发展已相对趋于平稳,但国际视角下发展趋势却日益恶化: 截至2020年3月9日,疫情已出现在全球102个国家和地区,其中意大利、伊朗和韩国等国家确诊人数均已达到数千人.如不采取紧急措施,COVID-19的全球流行趋势将日趋严重.考虑到疫情早期传播过程客观上更能反映其传染特征,为给国内可能产生的局部复发及国际疫情防控协作提供有意义的决策参考,利用当前相对丰富的病例调查数据,挖掘疫情在爆发初期的传染和域间传播规律仍有必要.
COVID-19的基本数据估计是研究的基础.来自《新英格兰医学杂志》的研究[1]对COVID-19早期的425名感染者的统计显示: 疾病平均潜伏期约为5.2 d,平均传染周期约为7.5 d,基本传染数(basic reproduction number,R0)约为2.2.Zhou等[2]利用公开新闻报道数据代入仓室模型得到了另一个可能的结果,他们初步估计,COVID-19的 R0值约为2.8—3.3,传播能力接近SARS.通过对“钻石公主”号邮轮个案的分析,文献[3]认为在95%的置信度下,R0的值约为2.28(2.06—2.52).然而该文献对每日感染人数的泊松分布假设并未得到其他文献印证,因乘客和工作人员陆续离船和核酸检测周期带来的时变因素也不能完全忽略.改进的仓室模型同样被应用于防控效果评价[4]和拐点预测[5].但传统的仓室模型并不能够模拟疫情在地域间的传播,《科学》杂志的一项研究[6]利用复杂网络对人类迁徙流动进行了分析,指出疾病的传播与城市间的“等效距离”,而非地理距离密切相关,而等效距离的核心构成因子是城市间的交通流量.因此,考虑人口迁徙的疫情传播模型得到了广泛关注,《柳叶刀》的一项研究[7]利用了航空网络人口流量数据和腾讯移动数据,通过一种考虑人口迁移的SEIR模型[6,8]首次对本次疫情的时空传播特征进行建模,得出了 R0的估计值为2.68,并预测疫情在全国的指数级爆发将会在1—2周后出现.然而该研究的主要问题在于,铁路而非航空才是国内春运期间的核心运力;假定武汉至其他城市的流量相等,与真实的域间交通流特征同样有着显著差异.Yang等[9]基于百度迁徙[10]数据和中国疾病预防控制中心(Chinese Center for Disease Control and Prevention,CCDC)每日公布的上报病例数[11],参照SARS的流行病学调查,利用深度学习的方法预测了COVID-19在国内和几个重点省份的发病曲线,认为疫情在4月底前难以完全平息.该研究的结果紧密依赖于百度迁徙规模指数,而该指数构造方法目前并未公开,与真实人口迁徙的关系并不完全明确.由于流行病学模型的预测结果通常显著依赖于初始系数的取值,以上研究在参量估值上的差异可能使得使用不同来源的研究结果大相径庭[12].更重要的问题在于,来自CCDC的针对截至2月11日中国内地所有报告病例的调查[13]证实,前期各项研究采用的上报日期数据与真实发病日期之间在时间和波形上均存在显著差异.作为真实发病日期的一种近似,确诊和上报日期存在的这种误差对前期各项研究的可靠性也提出了挑战.考虑到有限的医疗资源、社会承受力和行政成本[14],各级防控措施的介入时点和力度是另一个亟待研究的问题.管控介入时点的一个重要参考是疫情首次到达本地时间[15],Chen等[16]建立了全球流行病的城际传播模型,利用航空流量数据对疾病到达航空网中任一城市的时间进行了估计.该研究将城市间的交通流量以及疾病传染率定义为常数.而在真实环境下,传染率等关键参数通常是时变[17,18]的,且对于本次疫情而言,春运因素使得交通流量的常数假定也难以成立.通过以上分析可知,目前的研究集中于疫情基本参数的估计和疫情传播防控过程的建模和预测,且受限于早期相对匮乏的数据,进一步的有效性交叉印证和误差校正也有其必要性.
本文通过甲类传染病防控措施尚未启动时病例的回顾数据,首次利用病例的发病日期而非确诊上报日期,给出了未受干预条件下COVID-19传染能力估计,并利用一宗极端环境下的个案讨论了疫情的极限传染能力.在此基础上,首次给出了疫情蔓延至全国各省区的关键时点估计: 利用百度迁徙的公开数据和新闻报道数据推断湖北至各省区的真实人口迁徙流量,并与其他来源的公开报道数据进行了交叉校验;利用估计的参量值和人口迁徙流量构造了时域差分方程传播模型,用于推断其他地区首例病人到达时间,并将预测结果与收集得到的全国各省区首达病例时间做对比,验证了模型的有效性.本文的结论对复工复产复学过程中疫情局部复发的防控工作可能有所助益,也为疫情在域外的传播防控提供了参考.
2 疫情的初始传染情况估计
2.1 基本数据
来自CCDC最新文献的统计[13],截至2月11日,确诊病例共计44672人.从中可整理12月31日前病例发病日期统计如表1.
2020年1月1日以后的精确数据文献[13]并未给出,本文采用两种方法进行估计:
1)利用GetData Graph Digitizer软件抓取文献[13]公布的每日发病人数统计直方图,将其转化为近似数值;
2)利用文献[19]提出的蒙特卡罗方法,从该文献拟合的韦布尔分布中采样得到发病日期与上报日期的时间差,并结合CCDC网站[11]爬取得到的各地上报数据,反推出每日发病人数的估计值.
为校验方法的可靠性,统计两种估计方法得到的每日累积发病人数,依据文献[13]明确给出的1月10日,20日和31日数据推算的累积发病人数和对应日期上报CCDC的确诊人数如表2所列.
由于CCDC公布的确诊病例统计自1月3日开始,表中12月31日的上报人数以3日人数代替.表2有两点值得注意.第一,文献[13]数据与上报数据,特别是疫情前期的数据存在显著差距.其中一个重要原因是,文献[13]以发病日期统计病例,而CCDC网站以各地上报日期统计病例.这一差别极有可能增大前期部分研究的误差.考虑到真实发病日期更具参考意义,在此以文献[13]数据作为参数估计的基准数据.第二,表2的多数数据为某一区间范围.这是因为文献[13]百分比仅保留至小数点后一位,由此带来的舍入误差在早期病例数量研究中不容忽视,因此按照四舍五入的原则,反推出单项数据的上下限.从表2可以看出,无论是蒙特卡罗法亦或软件抓取法,所得数据与文献[13]给出的当日真实累积发病人数均较为接近,其参考价值可以互相印证.比较而言,软件抓取法的数值均落入依据文献[13]反推的区间内;且从2月11日的总计数据来看,软件抓取法获得的累积估计发病人数与截至当日的实际累积发病人数误差仅约0.04%;受2月11日将临床诊断纳入确诊依据这一重大变化的影响,12日新增确诊病例高达15153人,导致蒙特卡罗法在2月11日的估计误差达到了54.82%,因此本文采用软件抓取法的数据为基准.

表1 2019年累积发病人数Table 1.The cumulative number of confirmed cases in 2019.
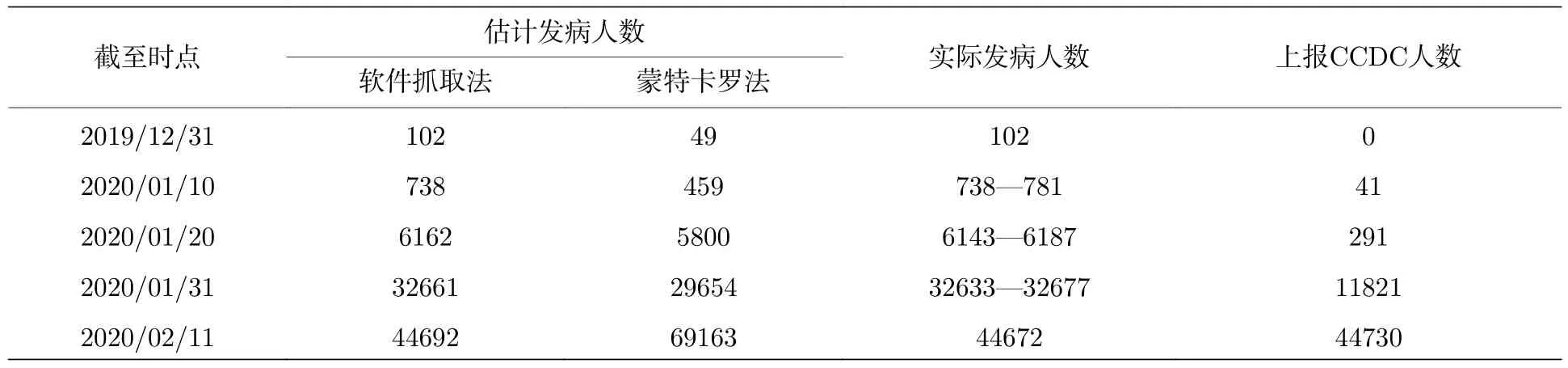
表2 2020年各时间段累积发病人数Table 2.The cumulative number of confirmed cases in each time slots in 2020.
2.2 一般情况下的传染率与基本传染数估计
仓室模型是目前流行病传播研究的主流方法之一.模型通常包括易感者(susceptible,S)、感染者(infected,I)、潜伏期感染者(exposed,E)和康复者(recovered,R)四类人群,根据考察目的的不同,可分别构成SI,SIS,SIR,SEIR等模型.考虑到疫情初期尚不存在,或极少存在康复者,且潜伏期感染者同样存在传染的可能,简化讨论起见,将潜伏者与感染者合并计算,并以SI模型模拟疫情初期发病情况.在此假定下,潜伏期对模型的核心影响可近似表达为时域上的平移,不影响其他参数的实质性讨论.令总人口为N;人群中初始感染者人数为 i0;传染率,即每名传染者每天使得易感者致病的概率为 β;则在时刻t,感染者的数量 it可表达为
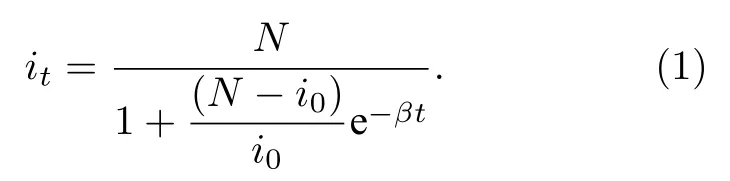
可见这是一个Logistic函数.将首次出现发病病例的2019年12月9日作为坐标原点,并考虑到我国在1月21日将COVID-19列为乙类法定传染病,并采取甲类传染病的防控措施,利用2020年1月21日及以前的数据进行估计.将N定义为武汉城市长期居住人口,公开资料显示约为1418.65万人.注意到截至12月31日疫情虽已传播至湖北部分市州,然而由于此时病例主要集中在武汉,且总人口基数足够大,使用武汉亦或湖北的人口数据为基数对估计结果不产生决定性影响.将表1和表2数据代入(1)式做回归分析,可得在不同时间点上,β的拟合值,95%置信区间与对应的拟合优度(goodness of fit,R2)如表3所列.
从表3中可以看出,即使在疫情早期数据不够充分,且受随机因素影响波动较大的情况下,模型的拟合优度最低亦能达到0.868;随着日期的推移,可以获取的数据日渐丰富,传染率 β 的取值从0.2213逐渐收敛到0.2060—0.2070,拟合优度也随之上升至0.999.可以认为SI模型能够有效模拟疫情早期的爆发情况.抽取表3中 β 在几个时间点上,包括12月31日,1月3日,1月9日和1月20日的取值对疫情做拟合,可得图1.
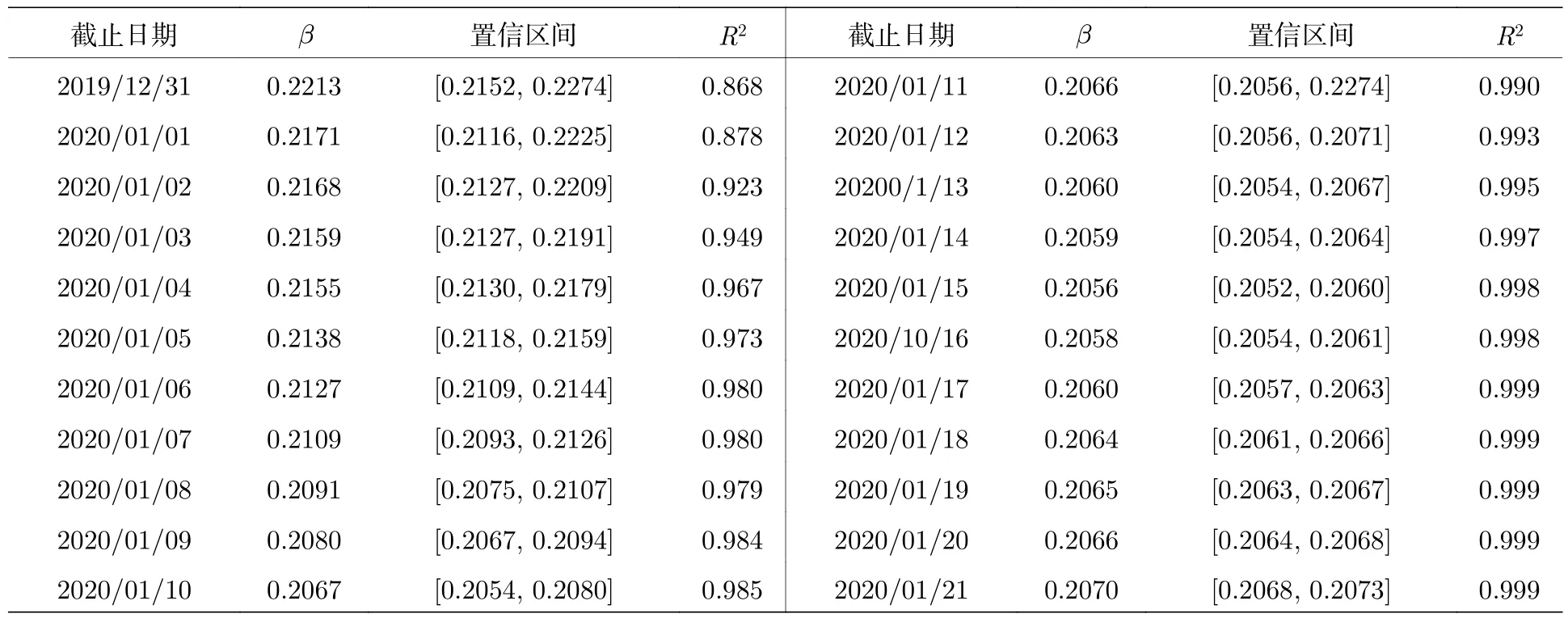
表3 传染率 β 可能的取值Table 3.Possible values of the infection rate.
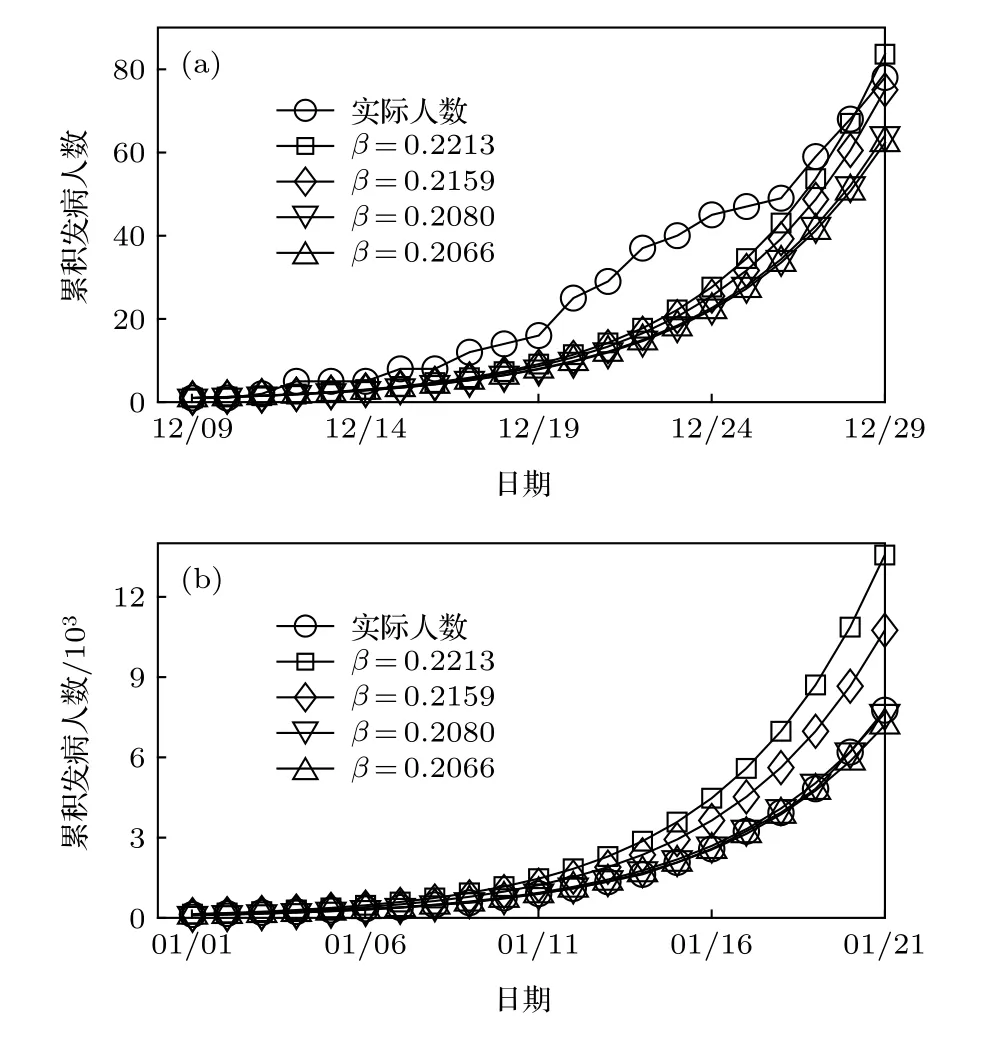
图1 不同的 β 取值下实际累积发病人数与预测发病人数的对比(a)2019年;(b)2020年Fig.1.Comparing the actual cumulative number of cases and its estimations according to different β :(a)Year 2019;(b)year 2020.
注意图1纵轴取对数.为便于观察,将几个重要的时间节点数据列于表4中.
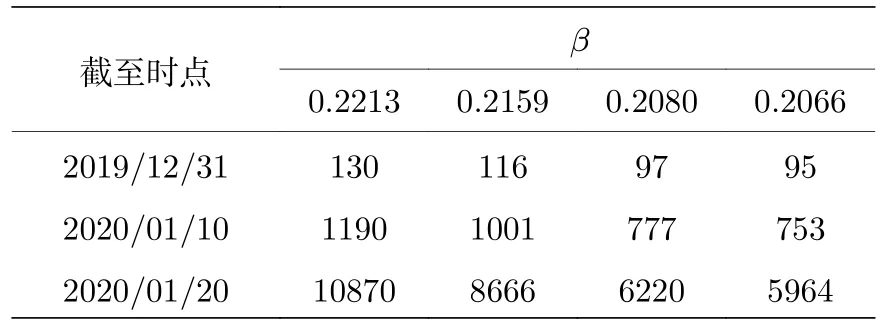
表4 重要时间节点的累积发病人数Table 4.Cumulative confirmed cases in key time nodes.
由表4可见,早期数据中存在的较大波动可能导致显著的计算误差.而代入1月10日和20日的数据后,无论取上限还是下限所受波动均在可接受的范围内.因此有理由将该表的结尾,即1月20日的 β 取值和置信区间作为传染率的有效估计.
一般认为基本传染数(basic reproduction number)R0的一个可行的计算公式为[20]

其中 Tg为平均感染天数,即病例从具备传染能力到康复或死亡而失去传染能力的平均时长.由此可得到 R0在疫情早期的一般估计.文献[1]给出的Tg可能的取值为7.5 d.《新英格兰医学杂志》最近的研究[21]对 1099个病例进行了调查,显示COVID-19潜伏期中位数和四分位距(interquartile range,IQR)为 4.0 d(2.0—7.0 d);自出现症状至发展为肺炎的中位数和IQR为3.0 d(1.0—6.0 d).由于COVID-19在潜伏期同样具有传染性,且从IQR来看,这两个数据均存在一定程度的右偏,有理由认为 Tg的取值为(4.0+3.0)d+右偏量,其后病人应已得到收治.通过不同文献的相互印证,可以推定 Tg=7.5的取值在当前研究阶段是有依据的.将1月21日估计的 β 取值和置信区间代入(2)式,估计对应的 R0为2.5525,95%置信区间为[2.5510,2.6555].
2.3 极端环境下的个案分析
截至目前本文的分析仅涉及了一般情况.全国范围内的复工复产目前已陆续展开,复学工作也在谨慎研究中.在特殊情况下,如环境更封闭(工厂车间)、人口密度更大(中小学与大中专院校)、人际接触更频繁(办公环境与写字楼)等,一旦爆发疫情,后果仍不堪设想.因此本文专门针对一宗封闭环境下中小人群聚集性疫情的个案进行分析.
据2月21日新闻报道[22],山东任城监狱发生聚集性疫情.监狱是典型的同时具备封闭环境、高人口密度和人际频繁接触等特征的研究样本,在此将其作为极端情况进行分析.相对于文献[3]研究的“钻石公主”号邮轮个案,监狱环境更加封闭,人口密度更高,且任城监狱的个案核酸检测周期较短,可以将“钻石公主”号邮轮因检测周期和乘客在长达10日内陆续离船导致的时变因素最大限度地排除.由于监狱在押人员数量和人员编制不属于政府公开信息,本文根据公开报道[23]进行侧面推算.该报道称,截至2月20日该监狱确诊病例207例,核酸检测人数为2077人,因此本文假定N=2077,it=207;同时有报道称2月初个别人出现咳嗽症状,因此假定 i0=1,坐标原点为2月1日,可得到t=19.考虑到缺乏数据的交叉印证,在此并未沿用文献[3]中以泊松分布拟合每日发病人数的方法,而采用了点估计,将t=19时的确诊人数 it=207直接代入(1)式进行求解,可得 β ≈ 0.2862;代入(2)式可得对应的 R0达3.1465,显著高于一般情况下的传染率.在此条件下,患病人数翻倍时间约为2.42 d.考虑到2077人的数量级与多数中小学或中等规模的工厂接近,这为我们敲响了警钟,日常生产生活中的疫情防控工作仍不能放松.
2.4 简要小结
本节估计,在95%置信区间内,未加人工干预时COVID-19的传染率 β ∈[0.2068,0.2073],其极大似然估计为 0.2070;进而推论 R0在 [2.5510,2.6555]间波动,极大似然估计为2.5525,与学界对SARS较为乐观的估计相近[24,25];作为一个可能的极限值,在极端利于病毒传播的环境下,R0可能达到3.1465,与SARS较为悲观的估计相近[26].虽较文献[2]的估计略低,但仍可得到相似的推论,即COVID-19属于传染性中等偏高的疾病.
3 疫情的时空迁徙特征
回顾SARS及本次疫情的流行过程,一个共同的特点都是从一点爆发,随着人员迁徙流动迅速蔓延至全国.显然,如果能够在疫情传播的早期切断域间传染途径,经济和社会承受的压力会小得多.因此研究疫情的时空迁徙特征,特别是爆发初期的特征十分必要.本节依赖前文的基础参量估计和百度公开的迁徙数据,构造了简易的时域差分方程模型,模拟了疫情早期的地域迁徙状况,并估计了各省级行政区域的首例病人输入时间.
3.1 迁徙流量的基础数据估计
百度迁徙网站[10]开放了2020年至今全国所有省区和地级市的迁徙规模指数,以及每个区域的Top 100人口流量百分比.其中迁徙指数和人口流量百分比均分别公布了迁入和迁出数据.通过对该网站的爬取,将元旦至春节百度迁徙规模指数与2019年同期数据进行对比,结果如图2所示.
考虑历年春运工作均围绕农历新年安排,因此以农历日期为基准进行统计.最新研究[27]认为虽然在关闭离汉通道前产生短暂的恐慌性迁出人流,但今年武汉春运期间的迁徙流量与往年相比没有显著的统计学差异,可以认为离汉人员主体是正常春节返乡人流.然而由于迁徙指数的构成目前并未公开,有必要对该指数与迁出人口的对应关系进行验证.
考虑到铁路运力是春运期间域间流动的主体,且历年春运中铁路运力的占比总体稳定,从公开的新闻报道中抽取了武汉市三大火车站(武汉站、汉口站、汉阳站)春节前的发送旅客人数.由于文献[27]验证了不同年份春运期间人口流量的相似性,丰富样本起见,同样抽取了2019年春运的报道,得到统计结果如表5所列.
限于信息采集手段,表5的数据缺失了部分日期的发送旅客人数.
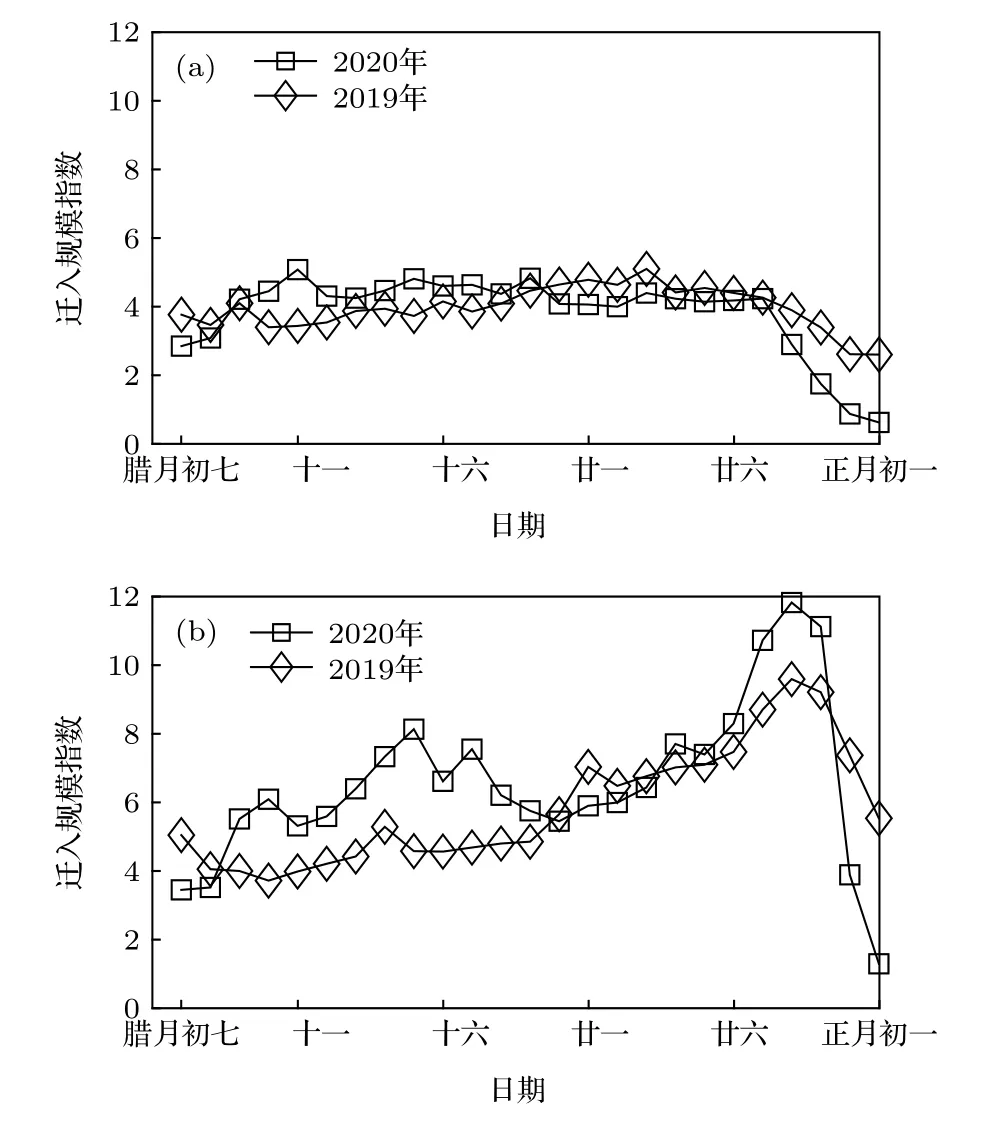
图2 武汉“封城”前夕迁徙指数与2019年的对比(a)迁入规模指数;(b)迁出规模指数Fig.2.Comparing the migration index of Wuhan before the spring festival with the same period of 2019:(a)Inner migration index;(b)outer migration index.
如表5所列,迁徙指数与三大火车站发送旅客人数之间的Pearson相关系数达到0.8408,二者呈强正相关;考虑到铁路的极限运力和反应滞后性(春运期间的车票预订因素),且1月22日宣布即将关闭离汉通道可能导致恐慌,将该点数据作为异常点剔除,重新计算的Pearson相关系数达到0.9108,故可以认为二者极强正相关.因此可以粗略假定区域j的迁徙指数Mj与实际迁徙人口pj满足线性关系:

一个重要的问题是参数k的取值.针对湖北省的全部市州和直属行政区(天门、潜江、神农架林区等),有

来自《荆州日报》和湖北省春运办的新闻报道称[28]: “春运首周,···截至 17日零时,全省铁、水、公、空发送旅客1050.7万人次”,可知

统计报道同期湖北省所有直属区域的迁出指数,可得

于是得到比例系数k的估计约为0.100679.
进一步,武汉市春运开始至封城期间的迁出指数合计107.116992,迁入指数合计56.4331536,可估计武汉市在此期间人口净流出为503.4815万人.该估计亦可与武汉市政府在1月26日的新闻发布会上公开的迁离人数相互印证[29],可以认为该推论具备一定的参考价值.
3.2 疫情到达时间推演
防控决策时需要回答的重要问题是,疫情将于或已于何时到达本地.在此,提出了一个简易的时域差分模型,利用迁徙数据,推导疫情首次到达特定行政区域的可能时间.
首先给出SI模型的差分形式:

当相对于 it-Δt和β,N取值极大,即易感者人数占绝对优势时,有便于计算起见,(7)式可近似为
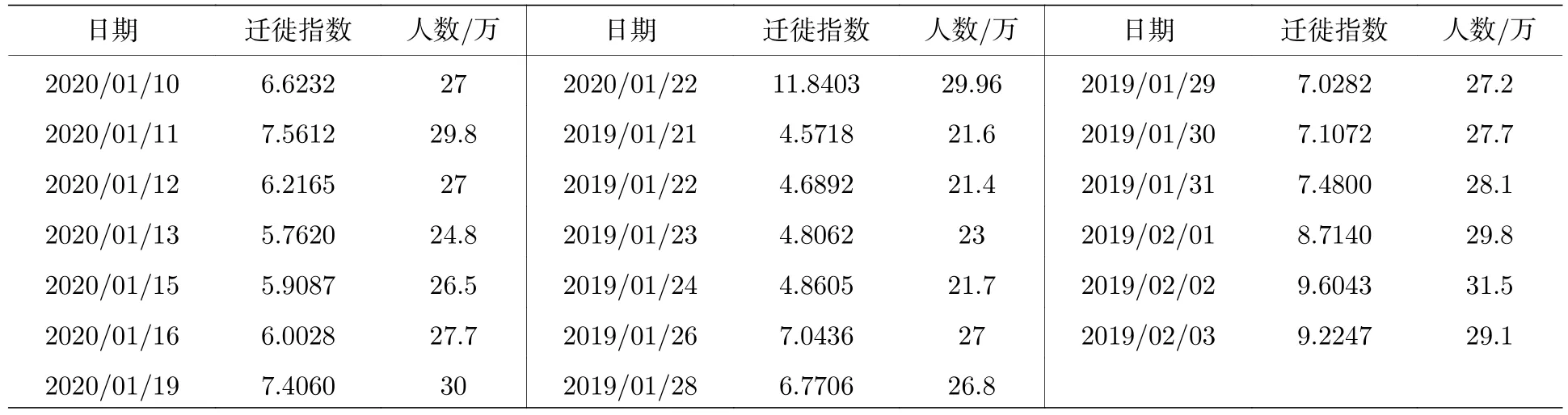
表5 武汉市三大火车站发送旅客人数与迁出指数Table 5.The Baidu inner migration index and the number of the travelers sent from Wuhan`s major railway stations.
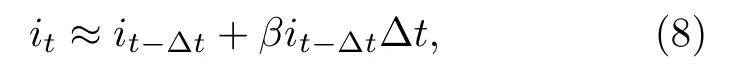
其中Δt定义为一个自然日,即满足Δ t=1 .当考虑人口迁徙因素时,假定人口迁徙概率与感染概率条件独立,对于区域j,有
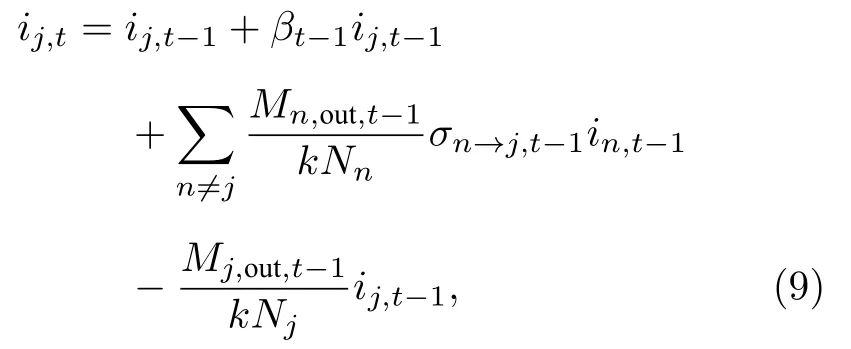
其中ij,t是区域j在第t天的感染人数;σn→j,t-1为第t—1天区域n向区域j流动的人口占区域n当日迁出总人口的比例;Mn,out,t-1为区域n在第t—1天的迁出指数;Nn为区域n的总人口数.由表3可知,由于传染率的估计会随着数据的丰富不断变化,为了拟合这种数据估计上的时变特征,在此将传染率 β改写为βt-1,即第t—1天统计发病人数得到的传染率估计.
根据文献[13],截至2019年12月31日湖北省共有14个县区报告病例.考虑到仅武汉市辖下县区级行政区域就有13个,可以认为在疫情初期,绝大部分病例集中出现在武汉市,因此仅考虑武汉向外省迁移的情况.
疫情首次到达模拟和判决的伪Python代码算法如下:

在此必须考虑,当疫情前期数据不够丰富时,传染率 β 的估计值可能不够精确,但此时却是实施决策的关键时刻,利用后期得到的传染率代入预测在决策时点上是做不到的.因此取多个时间点的传染率预测代入算法1进行仿真.本文取12月31日,1月3日和1月20日 β 的估计值代入计算.取1月3日的原因是,利用12月31日的数值预测,疫情将于1月4日蔓延至省外.因而3日可以作为决策前夕的关键时点.得到的结果如表6所列.
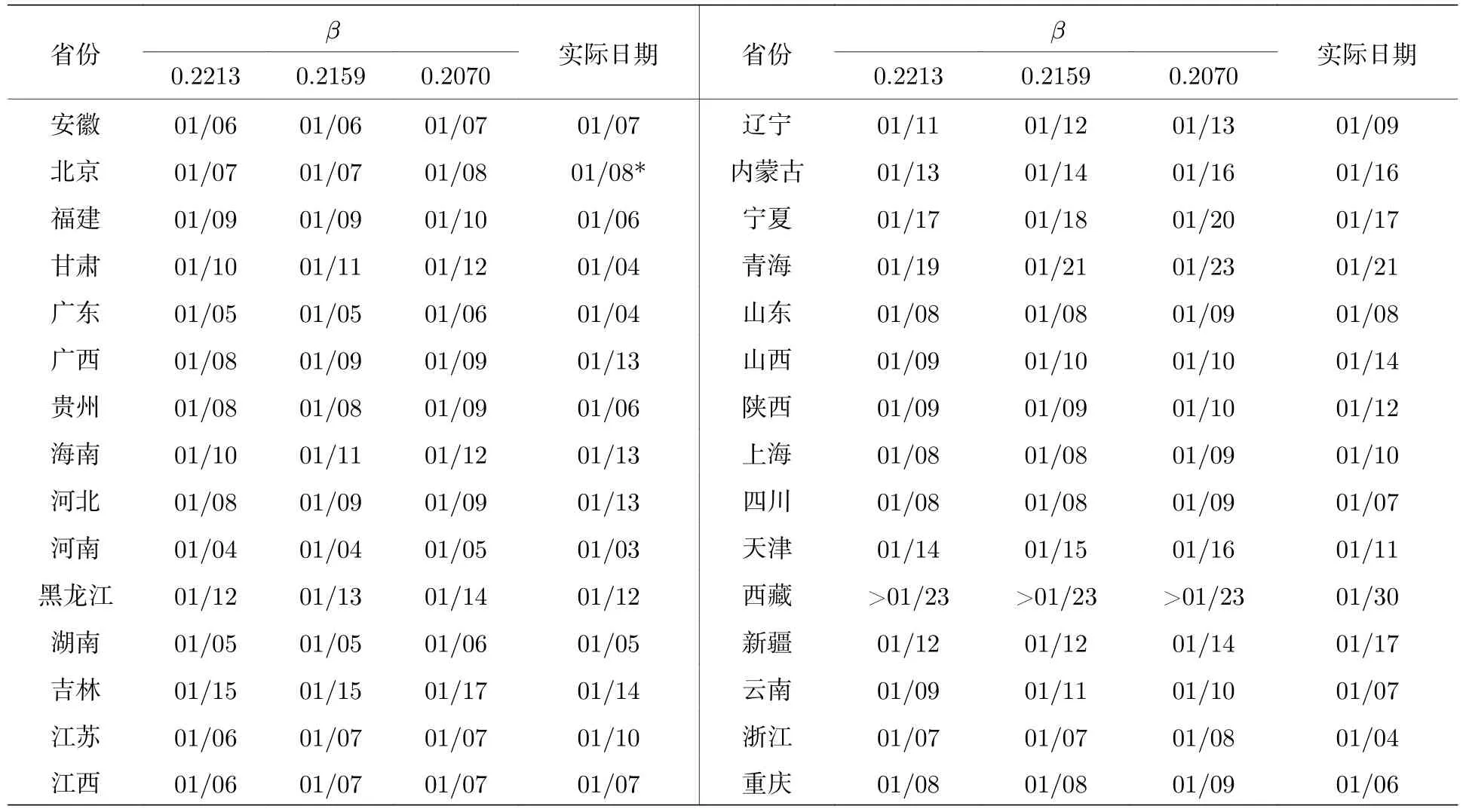
表6 省级区域的首例到达时间Table 6.The arrival times of each provinces.
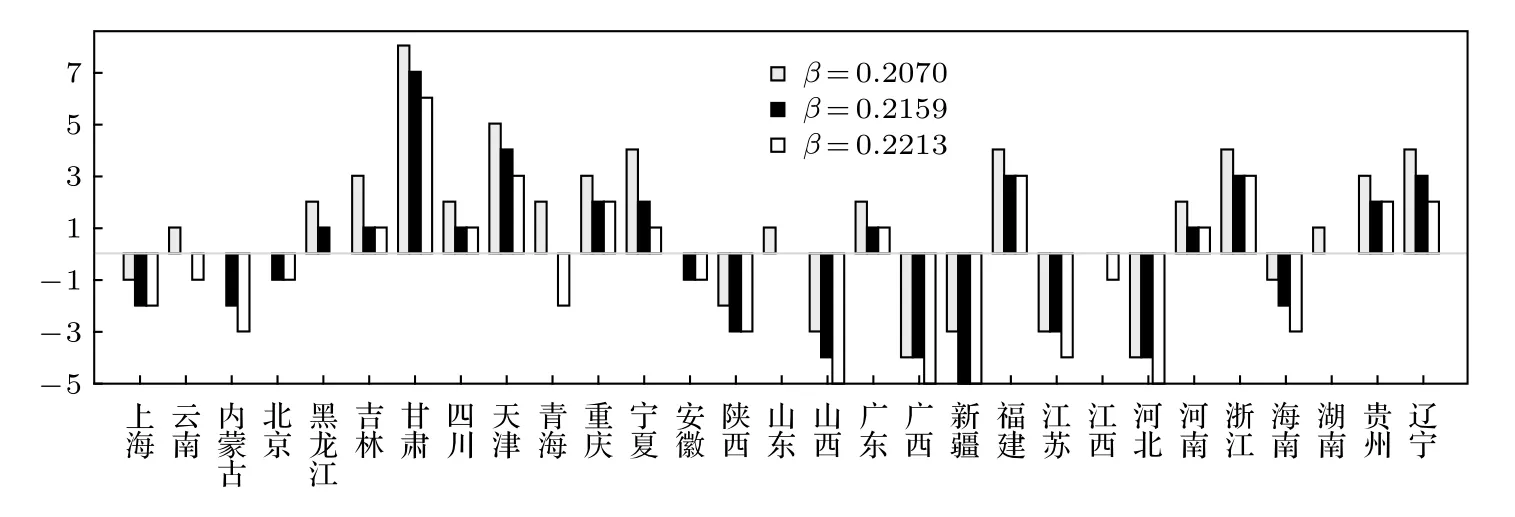
图3 各省区首达病例时间预测误差Fig.3.The estimation errors of the first arrival times for each provinces.
搜索各省级区域关于首例确诊病例的新闻报道,并与腾讯网“新冠肺炎确诊病患活动轨迹”专题[30]提供的病例轨迹数据合并,整理了病例抵达当地的时间填入表6中.表中海南和北京进行了特别标注,原因是: 虽然海南第124号确诊病例于1月2日自武汉返琼,但发病日期为2月5日,期间间隔35 d,超过了文献[1,21]报道的最长潜伏期,不应认定为输入病例,故将该省首达日期认定为第157号病例抵琼日期,即1月13日;北京市病例轨迹数据缺失,但据新闻报道[31,32],该市至迟1月8日凌晨即存在输入病例,在此取该日期作为首达日期;西藏自治区仅1例病例且到达于1月30日,其统计意义不足,予以剔除.
各省区病例首达时间的预测误差如图3所示.就已搜集的信息来看,模型对疫情向省外的蔓延时点的估计较为准确.基于12月31日的数据预测,疫情将于1月4日蔓延至省外.考虑到蔓延前夕的预测对决策最为关键,因此以1月3日的预测数据为例分析,疫情首先于1月4日蔓延到河南省,首达省份与模型预测一致,首达时间预测误差也仅有1 d.模型估计各省首达时间的平均预测误差为2.14 d,其中有 41.38%的预测误差 ≤ 1 d,79.31%的预测误差 ≤ 3 d;除甘肃外,所有省份的首达时间预测误差均 ≤ 5 d,反映了模型的有效性.考虑到各省最早上报病例日期为1月19日,相对在省外蔓延的确切日期滞后16 d,采用模型预测得到的理论预测值显得更有价值.即使择取12月31日和1月20日的模型参量估计也可达到较好效果,其中预测疫情蔓延至省外的时间误差分别为1和2 d,首达省份预测无误;平均预测误差也仅为2.31和2.48 d.表6可能反映的另一个沉痛的现实是,在迅猛发展的疫情面前,强力交通管制措施采取的时间同样显得滞后.如果根据模型的预测,将强力交通管制措施提前到1月4日,即模型预测的即将蔓延至省外的时间施行,则可有效阻断疫情在除河南外全部省份的蔓延.
4 结 论
本文利用最新的流行病学调查,取疫情尚未得到有力干预时的数据代入动力学模型进行拟合,给出了传染率和基本传染数的一般估计.为模拟复工复产复学过程中可能出现的聚集性疫情特征,利用公开报道的极端环境个案,给出了可能的传染率和基本传染数上限.在此基础上,综合流行病学调查数据、互联网爬取数据和公开新闻报道数据,在佐证百度迁徙规模指数参考价值的前提下,估计了疫情发源地迁至各地的绝对人口数量,代入设计的时域差分模型,模拟了疫情初期在地域间的传播过程,给出了疫情首次到达各省级区域的时间估计,并与新闻报道数据做比对,验证了模型的有效性.
本文的创新在于: 首次以流行病学调查中公布的发病时间,而非确诊和报告时间为基准进行疫情推演.相较于两个时间节点间约10 d的错峰,这一选择显然更具合理性;给出了已得到初步应用的百度迁徙规模指数的有效性验证,侧面证实了它与人口迁徙规模的粗略线性关系;利用人口迁徙数据,首次给出了疫情到达全国各省的时间预测.有限度使用新闻报道数据以改善疫情初期科研数据尚不够丰富的现状也是本文的一个特点.
本文还存在以下不足,将在后续工作中改进:本文依据的流行病学调查数据更多依赖于患者个人回忆,可能存在时间偏差,需要更加精确的数据进行进一步验证;本文提出的方法对疫情爆发后强力防控措施介入条件下的推演偏差可能较为显著,应重点思考优化方案;如何对各级力度的疫情防控措施进行量化分析与效能评价,在有效控制疫情的前提下做到松紧适度,降低对经济社会的负面影响,也是一个值得研究的问题.

