太阳电池翼在轨模态光学测量优化的计算机辅助方法

王 威，臧 旭，郭其威，张美艳，唐国安

（1.复旦大学 航空航天系，上海 200433；2.上海宇航系统工程研究所，上海 201109）

0 引言

柔性电池翼是空间站的重要组成部分，其动力学特性影响着空间站的姿态控制［1］。空间站运动状态变化产生的动态激励，同样引起柔性电池翼的持续振动，由此产生的交变应力可能导致柔性电池翼自身或与空间站的链接件损坏，破坏空间站的正常工作，且在设计计算时，其频率特性也会影响到减振参数设计［2］。因此，掌握这些柔性附件的动态特性是非常有必要的。我国借鉴国际空间站成功经验，采用“Mast”+“Blanket”柔性电池翼的设计方案［3］。

随着计算机技术的迅猛发展，有限元法已成为预示大型挠性结构动力学特性的主要手段［4-8］。大多数科研工作者采用混合坐标法或假设模态法研究柔性翼这类柔性结构的动力学建模问题，重心偏向于研究中心刚体的大范围运动与柔性附件的弹性变形运动之间的刚柔耦合现象［9］，所采用的简化模型大多是柔性梁或柔性板，其精度需要通过实验验证。

柔性电池翼具有展开面积大、刚度低等特点，在地面进行展开状态模态试验时受重力［5，10］、悬挂系统及空气阻力等因素的影响极大，测得的模态参数与在轨状态的结果有一定差别［11］，因此，需要在轨实验。

实验中对模态的测量可分为接触式测量和非接触式测量两种，且这两种测量方式都发展得非常成熟。相比于前者，非接触式测量具有不与被测物体直接接触而不产生附加误差、测量速度快、采样频率高、量程大等优点，被越来越多地运用于实验中［12-14］，且在柔性翼的在轨测量实验中也被广泛应用［15-17］，郎燕等［18］为提高测量精度也提出了优化方法。然而，在轨模态分析试验采用非接触式光学测量时，上述文章中并没有提及如何选择靶标位置、相机选择及外参系数设置是否合理等问题。同时，可供相机安装的位置非常有限，从相机观察柔性翼整体时，由于动态激励下柔性翼不同位置的响应结果相差较为悬殊，导致信噪比不同，即使响应结果相同，靶标处于不同位置测得结果误差也不一样。为了充分利用空间站在轨状态的有限资源，优化相机安装位置和视角以及评估在轨模态试验方案的有效性，有必要利用计算机图形学方法，结合有限元瞬态响应计算结果，对柔性翼在轨模态非接触测量的光学拍摄过程进行仿真，并建立相应的软硬件平台。

本文基于空间站柔性翼的有限元模型，先采用MAC.Nastran有限元软件，求解出柔性翼在动态激励下瞬态响应的动力学参数；然后借助计算机图形学软件OpenGL对上述结果进行可视化设计，生成不同位置、不同视角等相机参数下柔性翼的变形图像，并获取靶标在像平面的投影轨迹；随后重构出靶标的动态位移曲线，并与有限元计算结果对比，从而评估测量方案。本文充分利用动力学仿真成果，结合光学仿真，以靶标的投影轨迹长度预先对柔性翼在轨模态的测量方案做出评估，得出有限实验方案的条件下的最优测量方案。该方法可发展为计算机辅助试验的一种手段，为航天器柔性翼在轨模态测量方案的选择提供理论依据，从而弥补无法地面实验的不足。

1 柔性翼在轨激励动态过程的力学仿真

柔性翼结构如图1所示，其由柔性阵面、张紧机构、伸展机构、收藏箱、收藏筒和驱动机构等组成，宽度超过6 m，总长接近30 m。

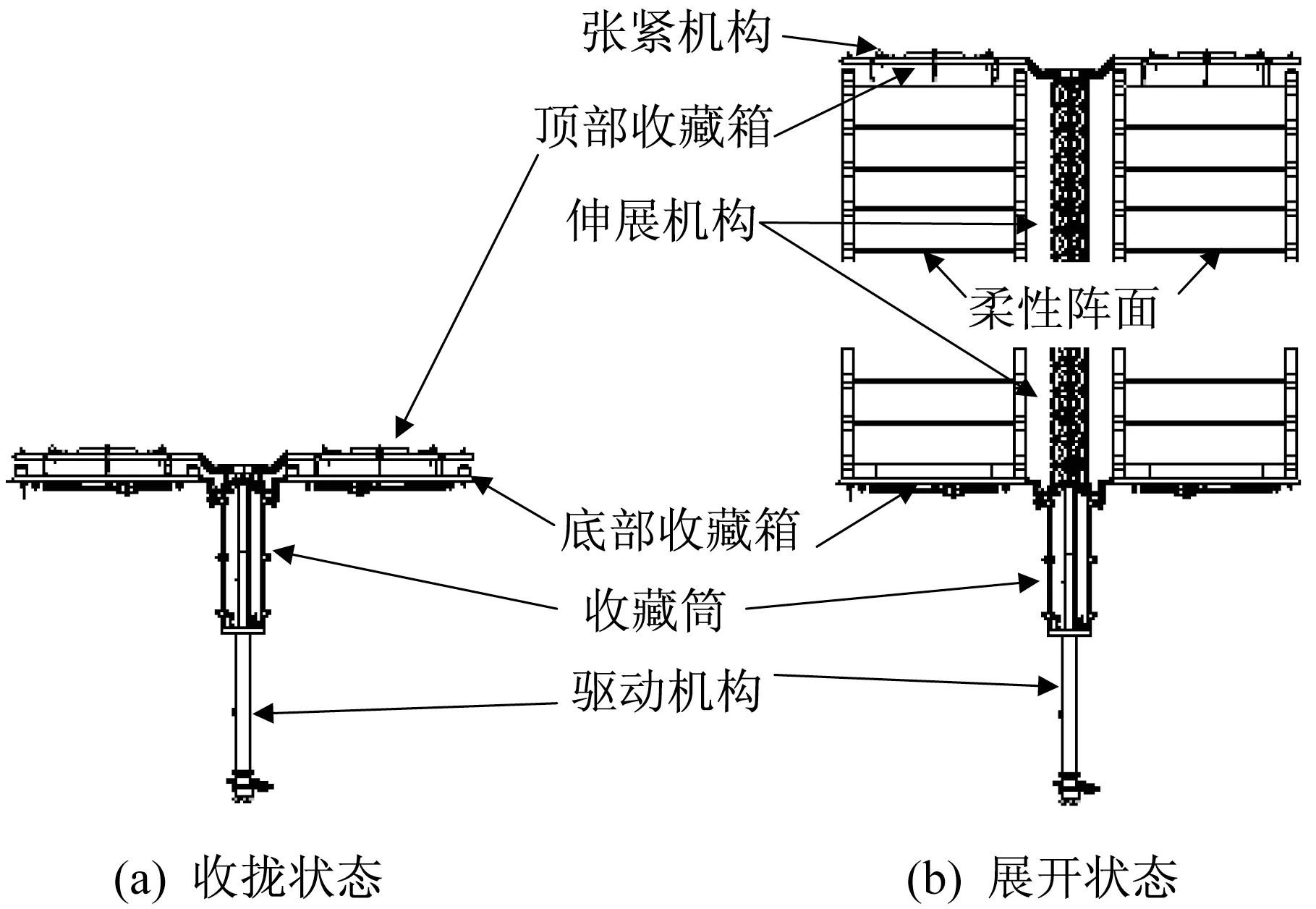
图1 空间站柔性翼结构-机构Fig.1 Mechanism diagram of the space station flexible solar array structure

郭其威等［19］对柔性翼有限元模型进行了在轨工况激励下的瞬态响应过程的数值仿真。仿真时，电池翼模型与本体在驱动机构连接处（根部）分离。根部的加速度a(t)、角速度ω(t)和角加速度α(t)作为数值仿真的输入条件。

参考以根部为原点，随本体一起运动的非惯性坐标系O-xyz，柔性翼上任意质点做非惯性运动的加速度，可表示为

式中：r(t)为质点关于坐标原点的矢径，为时间t的函数。

典型的在轨工况包括变轨、对接和分离等，加速度时间函数如图2所示。

图2 空间站柔性电池翼根部的加速度输入条件Fig.2 Acceleration input conditions of the space station flexible solar array root

根据根部的输入条件，利用有限元分析程序能计算得到柔性电池翼各处的动态位移响应结果。为了模拟光学成像效果，在柔性电池翼有限元模型上选择若干节点作为测量用的物方点，如图3所示。物方点用编号1～15标识，其中1～5位于伸展机构上，6和8以及7和9位于上下收藏箱的两侧，10～15分布在柔性阵面上。

图3 光学测量物方点在有限元模型中的位置Fig.3 Physical point positions in the finite element model during the optical measurement

使用MSC.Nastran进行柔性电池翼的瞬态响应分析，从结果中提取物方点所在节点的响应数据，得到动态位移曲线，如图4所示。各个物方点的响应数据表明，柔性电池翼振动以一阶阵型为主，频率约为0.044 Hz。拍摄对象以较低的频率作低速运动，有利于基于双目相机的光学测量实施。对比如图3、图4所示的物方点布局和响应函数可知：主伸展机构、顶部收藏箱上物方点（5、7、9）和柔性阵面上的物方点（10、13）的振动幅度较大，便于根据成像后的相差测量其位移。但如果相机布置在靠近本体附近，由于近大远小的透视关系，这些物方点成像后的绝对距离则较小，也影响测量精度。伸展机构和底部收藏箱上物方点（1、6、8）则相反，靠近本体，但振动幅度较小。柔性面的运动是自身相对运动和伸展机构牵连运动的叠加，振幅最大点在阵面的中部偏上处（如物方点13）。

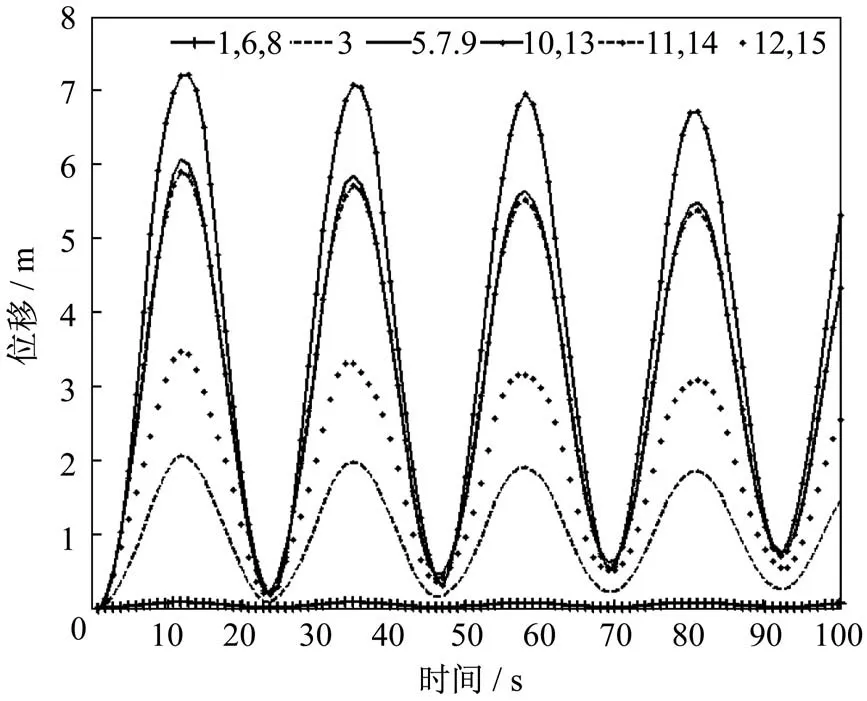
图4 物方点瞬态响应的有限元仿真结果Fig.4 Finite element simulation results of the physical point transient responses

通常在本体附近容易安装相机，但本体附近物方点的响应幅度较小，而远离本体的物方点响应幅度大，相机安装或拍摄难度相对较大。这些矛盾需要将有限元力学仿真与光学成像仿真相结合，得到不同输入条件下物方点的最终成像效果，综合分析相机-物方点布局，以及镜头焦距、传感器分辨率等参数对测量精度的影响，进而优化测量方案。

2 柔性电池翼动态变形的光学仿真

在柔性电池翼瞬态响应的动力学仿真基础上，可进行成像过程的光学仿真。光学仿真就是根据设定的焦距、视角、分辨率等参数，将柔性电池翼瞬态响应可视化，模拟相机的拍摄过程。物方点（包括靶标、定义模型的节点等）经过相机镜头摄影后成像在像平面上，理想的投影成像模型是几何光学中的小孔成像模型，其本质是射影几何中的中心透视投影过程。基于光学测量的在轨实验模态分析的场景示意图如图5所示。相机安装位置、焦距、视角等是需要优化的试验方案参数。

图5 基于光学测量的在轨实验模态分析场景Fig.5 Schematic diagram of the on-orbit experimental modal analysis scenario based on optical measurement

整个场景的建模参考统一坐标系O-xyz，称为世界坐标系。在世界坐标系下，相机的安装位置用pC(xC，yC，zC) 表 示，相机的光 轴方向用目标点pT(xT，yT，zT)定义：光轴指向从pC到pT。因此，相机坐标系的一个基矢量可以表示为

式中：l3、m3、n3分别为基矢量w的坐标分量。

为了指定相机的转动方向，可以在位于光轴与相机上方的平面内选择一个“上方向量”a，该向量在世界坐标系下的分量是(ax，ay，az)，那么相机坐标系的另外两个基矢量u和v可按如下规则确定，即

式中：u′=w⋅a=[m3az-n3ay m1ax-n1az m2ayn2ax]T；l1、m1、n1为基向量u分量；l2、m2、n2为基向量v的分量。

将相机取景范围内任意一个靶标p在世界坐标系、相机坐标系下分别记为(xw，yw，zw) 和(xb，yb，zb)，若采用齐次坐标，两个坐标分量的变换关系表示为

式中：M1称为世界坐标系到相机坐标系的变换矩阵，也称作相机外参数矩阵，可以由基矢量u、v和w的分量确定，即

实际上，相机的成像平面（即传感器）位于w轴正向。但为了便于数学上的描述，等价地将成像平面置于w的负向，如图6所示。设成像平面与相机安装位置pC的距离为f（也称作焦距），根据射影几何的透视关系，任意点p在成像平面上的投影点q就是pC与p连线与成像平面的交点。据此，可算得投影点q(xq，yq，zq)在相机坐标系下的分量为

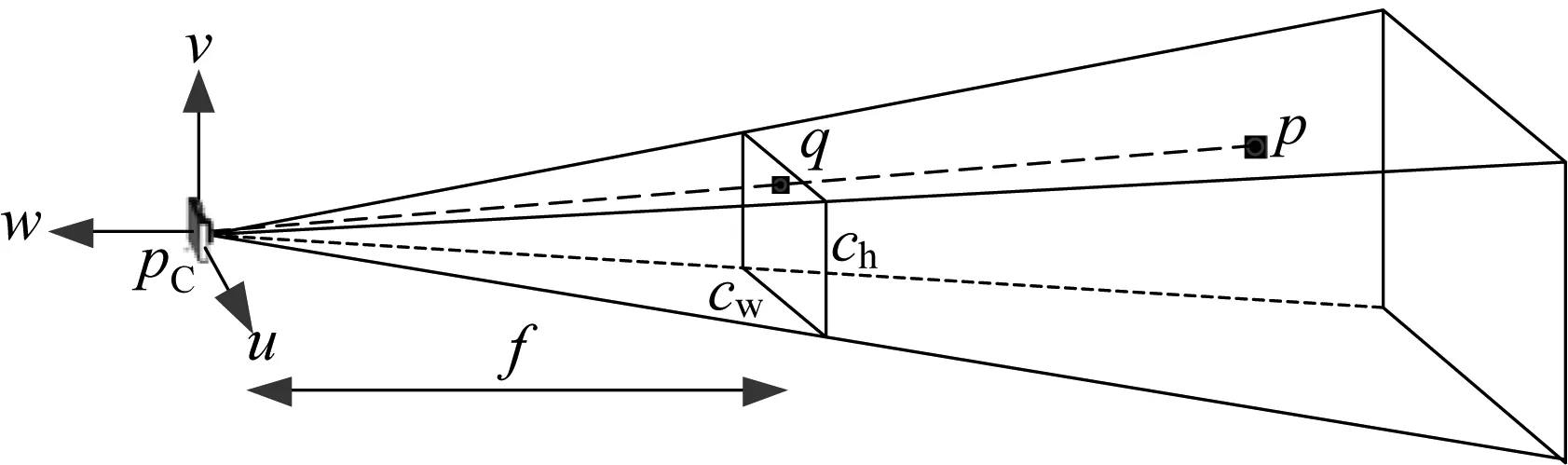
图6 相机透视投影视图Fig.6 Perspective projection view of the camera

若不考虑消隐、光照等图形学效果的处理，坐标分量zq不再参与计算，故可以将其忽略。将式（6）中的前两个变换表示成

式中：投影变换矩阵

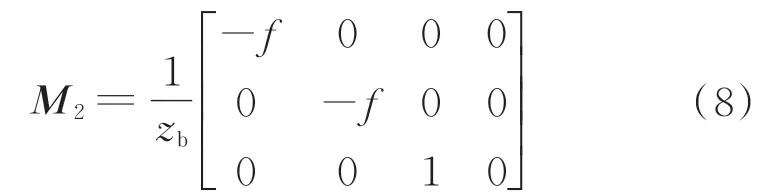
在计算机图形学中，为了能适应不同的显示设备（当前问题中为传感器的不同分辨率），需要将投影点q用归一化坐标表示为

式中：

式中：cw、ch是显示设备（底片）的长度和宽度。常规设备（底片）的显示区域都是矩形的，归一化后xn、yn的范围是[-1，1]。当应用到具体设备时（例如相机的传感器），将长度和宽度方向上的像素个数分别记为Nw和Nh，那么投影点q在设备坐标系下的像素位置（用齐次坐标表示）为

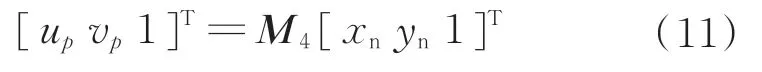
式中：

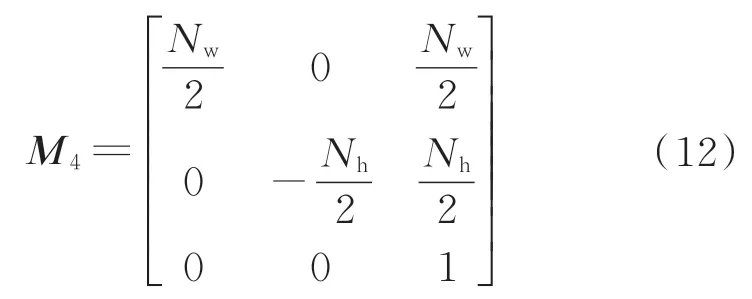
综上所述，任意点p在建模时采用的世界坐标系分量与最终在相机传感器上的像素位置的变换关系为

式中：M=M4M3M2M1为总的3行4列变换矩阵；(up，vp)为任意点p的像素坐标。

柔性翼的有限元模型都是由点（集中质量）、线（杆梁）、面（板壳）或实体单元构成。所有单元的具体位置都用节点的世界坐标系分量表示，根据式（13），也便确定了它们在相机传感器上的像素位置。只要将在轨激励下瞬态响应得到的位移函数迭加到柔性翼模型的节点坐标上，即可实现该瞬态响应过程的光学仿真。

3 坐标重构与光学效果评价

以郭其威等［19］的柔性电池翼有限元模型为例，世界坐标系建立在如图3所示的主伸展机构的根部，用有限元分析程序MSC.Nastran计算后可以得到某个在轨激励条件下模型中所有节点瞬态响应的位移时间函数。布置两个相机构成双目光学测量系统，利用相差从靶标的二维投影图重构其世界坐标的三维分量。

光学成像过程的仿真基于OpenGL图形标准，在Visual Studio 2010开发平台上，以Windows应用MFC实现。两个相机和目标点位置由OpenGL函数glulookat定义，相机焦距等参数由函数glperspective定义，相机传感器的像素在MFC初始化窗口时定义，相机1和相机2的完整参数见表1。

表1 相机参数设置Tab.1 Camera parameters for shooting

如图7所示的4幅图像分别为相机1和相机2在第0秒（初始状态）和第11秒所拍摄的柔性电池翼瞬态振动型态的光学仿真图，其中黑白格表示各个靶标。

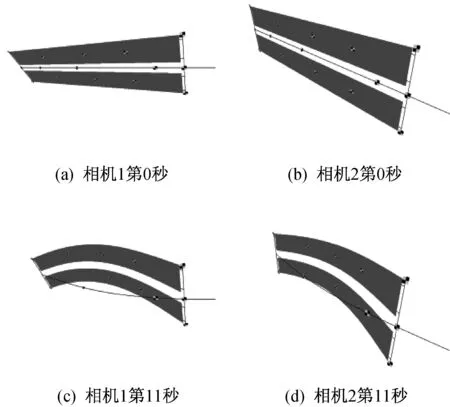
图7 光学仿真柔性电池翼拍摄效果图Fig.7 Shootingeffect pictures of theoptically simulated flexible solar array

同一个靶标在世界坐标系下的三个坐标分量xw、yw和zw是唯一的，经两个相机成像后的像素位置是不同的，分别记为(up1，vp1)和(up2，vp2)。靶标在不同相机中投影后的像素位置差异可用于重构三维坐标。将由式（13）表示的相机1、相机2的变换矩阵分别记为M(1)和M(2)，分量是m(1)ij和m(2)ij(i=1～3；j=1～4）。那么式（13）表示的世界坐标分量和像素位置存在关系可以表示为［20］

其中，

采用最小二乘法求解超定方程式（14），可通过像素坐标(up1，vp1)和(up2，vp2)重构出靶标点在世界坐标系中的三维坐标(xw，yw，zw)。

当面向柔池电性翼的模态分析问题时，重构对象不仅仅是靶标的世界坐标，而且还需靶标的三维移动分量（即位移向量）。根据式（13），容易算出靶标的像素位置，将不同时刻的靶标像素显示在同一张点阵图上（如图8所示），就能得到柔性电池翼的靶标的运动轨迹，图8中的数字是靶标的编号。

图8 光学仿真拍摄效果Fig.8 Shooting effect pictures of the optical simulation

点阵图上靶标运动轨迹的长度可大致表明位移向量的可辨识程度，即长度越大表明位移辨识精度越高。为了凸显动态位移效果，用*号标记表示靶标在图像传感器上的初始位置，+号标记则表示拍摄结束时的位置，浅色线段是运动的靶标在图像传感器上留下的轨迹。由图8可见：靶标13的运动轨迹最明显，位移的可辨识性好；靶标1的轨迹不明显，位移的可辨识性较差；而靶标3则介于它们之间。三维计算机图形学的显示还包括消隐功能，若建立更为详细的电池翼模型，那么靶标的运动轨迹还可能出现被遮挡现象，如图8（a）所示相机1显示的结果中，靶标4和9表明部分时段无法被检测到，这也是试验方案需要评价的内容。

仍以靶标1、3和13为例，三维重构后得到瞬态响应结果如图9～11所示。在图9～11中，实线是有限元仿真的结果，可作为电池翼上靶标的“实际”运动时的响应曲线，o型标记为采用双目视觉三维重构得到的动态位移。

重构精度对比结果见表2，可见靶标的可辨识程度随着振幅的增加而逐渐增大，因此，重构结果的效果与投影轨迹的分析结论一致。靶标的轨迹分析所涉及的图形旋转、投影变换等属于正问题，而三维重构所涉及的图像处理、超越方程求解等属于逆问题，前者的运算复杂度低于后者。因此，在制定试验方案时，用力学仿真与光学仿真相结合的轨迹分析方法能对靶标布局、相机安装位置和参数设置做出快速的评价。

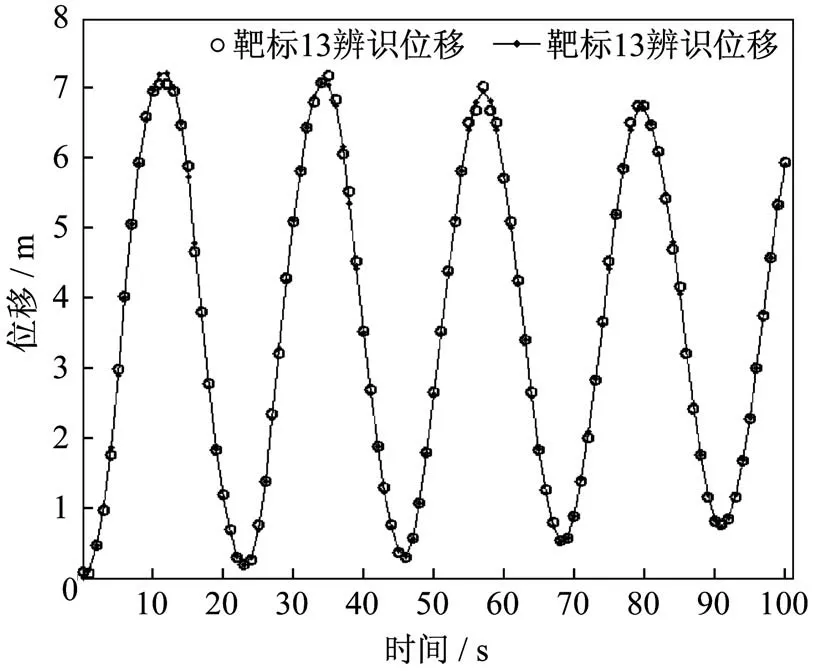
图9 靶标13：基本可完全辨识Fig.9 Target 13：almost completely recognizable

图10 靶标3：可部分辨识Fig.10 Target 3：partially recognizable

表2 重构精度对比Tab.2 Comparison of reconstruction accuracy

图11 靶标1：完全不可辨识Fig.11 Target 1：completely unrecognizable

4 结束语

利用空间站在对接/分离/变轨过程中柔性电池翼受激励产生的大幅度动态位移，采用对双目点阵图像进行三维坐标重构的非接触测量方法，是实现在轨电池翼实验模态分析的一种可行的途径。本文将对柔性翼动态响应的有限元力学仿真与成像过程的计算机图形学仿真相结合，根据靶标在图像传感器上的运动轨迹长度的可辨识性，对基于光学测量的试验模态分析方案进行快速评估，进而在测量方案实施前进行评估优化，属于计算机辅助实验系统的组成部分，能充分利用结构动力学仿真成果，弥补大型柔性部件地面实验的不足。