基于高渗透可再生能源分层分区并网节能规划

温新　邵科　王念念　王一帆

摘 要

针对加入可再生能源后的配电网规划和系统优化问题，提出了一种考虑投资成本的和节能效果的分层分区规划模型。上层规划在规定总投资成本的目标函数后，考虑了可再生能源的接入规划和相应的约束条件，下层从储能的加入和线损最小为目标函数，通过上层给定的电源规划下计算最小网损，生成最优的组合方案。

关键词

配电网;可再生能源;二层规划模型;节能规划

中图分类号： G633.6                        文獻标识码： A

DOI：10.19694/j.cnki.issn2095-2457.2020.04.70

0 引言

现代社会对电力供应的可靠性、无污染性要求的提高，传统火力发电所带来的环境污染、全球气候变暖等问题越来越被人们所重视。由于无法灵活跟踪负荷网的变化，所以采用清洁性能源的分布式发电得到了快速发展。

研究表明，针对同一线路不同的节能手段降低损耗的潜力不同;同一种节能手段针对不同的线路运行条件，节能潜力依旧有较大差距。因此，通过对不同节能技术手段在不同线路上节能潜力的对比分析，有助于节能方案的高效实施。

如今，配电网节能任务中考虑了电源的影响，例如在模型中加入的电源位置和容量的不相同，将带来不同的线损方面影响。文献[1] 搭建了最小化配电网有功网损、电压偏差和静态电压稳定指标的多目标优化的模型，并兼顾了配电网运行经济、安全和稳定性。文献[2]把配电网运行的经济性和电压质量当作目标，并将多场景的分析运用在其中。基于以上分析可知，当可再生电源接入主要会对网络损耗、潮流分布情况等方面产生影响。这些因素的改变会影响整个系统的运行成本增加。因此本文主要从DG的投资运行成本、发电成本等方面建立优化配置电源模型

本文下层模型以电网损耗为目标函数，综合考虑原有网络结构的电网损耗，借鉴引用改进遗传算法进行重构，在结合节点电压幅值保证、最大输送容量等因素，重构优化模型，实现网损最小化。

基于以上分析，本文提出了一种高渗透可再生能源分层分区电网并网节能规划方法。首先从DG的投资运行成本、发电成本等方面建立优化配置电源模型，然后综述近10年来传统配电降损法及含有分布式电源的配电网优化配置研究成果，通过建模分析配电网中光伏电源容量、位置、运行方式对配电网网损的影响。

1 节能规划模型

1.1 分层分区节能规划思路

首先对待改造区域的电网依照供电片区或变电站实行解列分区成各子区配网，之后根据子区配网节能指标的情况，建立双层规划模型。上层模型考虑电源规划接入点位置和容量，计算总投资成本。下层模型考虑降损方案，运用改进遗传算法，计算电网总网损值。

1.2 接入分布式可再生能源的网损变化模型

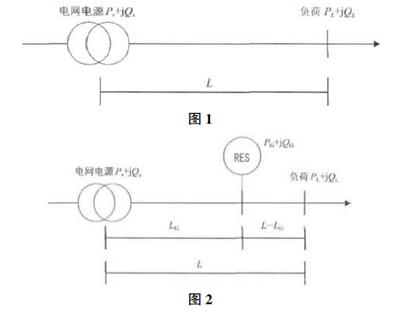
在简单的潮流计算中，电网负载端的消耗由电源端单独提供，而引入分布式可再生能源后，电网消耗由电网电源与分布式可再生能源共同提供。本文采用文献【3-4】的模型，运用数学分析推导出影响电网损耗的影响因素。在负荷大小相同，不考虑线路压降以及三相不平衡的情况下，建立的理想模型图1和图2。设全线路电压为U0，其中，Ps、Qs分别代表电源的有功功率、无功功率;Pl、Ql分别代表负荷的有功功率、无功功率;PG、QG分别代表可再生能源电源（RES）有功、无功功率;L代表电网电源与负荷之间的距离;LG代表电网电源与可再生能源电源（RES）之间的距离。

通过接入可再生能源，电网网损可以得到有效降低，因为可再生能源可以改变电网的潮流构成。无可再生能源接入的系统中，电网电流大量在线路中流动，造成较大的线路损耗，而加入后负荷所需用电，一部分由电源供给，另一部分改为由接近负载端的可再生能源提供。

1）系统流入负载的单项电流：

假设线路单项阻抗率为r0（Ω/km）未接入可再生能源时，IS=IL，电网损耗为：

2）接入可再生能源后单项电流为IG：

所以电源单独提供的电流Is：

此时电网损耗将分为两个部分：

3）可得是否接入可再生能源，电网网损差值为：

由式可知，电网网损因素与可再生能源接入处与负荷距离（LG）、接入可再生能源的功率（PG）、无功功率（QG）相关。

1.3 各个影响网损因素的分析

1）可再生能源的接入位置

由网损差值式可知，当接入的可再生能源容量以及功率因数不变时，△S的大小仅与LG的大小线性相关，LG为电网电源与可再生能源接入之间的距离，当LG越大，及可再生能源越接近负荷中心时，△S越大。

2）可再生能源相对负荷容量

由网损差值式可知，当考虑可再生能源相对负荷容量对网损影响时，控制可再生能源的位置及功率因数为一定值，即设LG为常数;设可再生能源相对负荷的比值为K，即：

可见，当K=1时，△S最大，即此降损最优;当K=2时，△S=0，表明此时无降损效果;当K>2时，网损将大于未接入可再生能源。

所以当可再生能源容量与负荷的容量相当时，可使配电网损耗最小。

3）可再生能源运行时功率因数

由网损差值式可知，此情况下要控制可再生能源位置及容量不变，设PG=SGcosφ，QG=SGsinφ（φ为可再生能源系统功率因数角），则无功功率略多时会减少系统损耗，可再生能源发出的无功功率补偿了负载所需的原本在电网中吸收的无功功率，从而无功电流减小，减小电路的有功损耗。若要为电网提供无功支撑[5]，可采用目前常用的恒无功功率Q控制[6]、恒功率因cosφ控制[7]、基于并网网点电压幅值的cosφ（U）[8]

1.4 上层规划模型

1.4.1 目标函数

本文将DG接入配电网，以总成本最小化为目标建立模型：

minF=min（F1+F2+F3）

式中：F1为可再生能源的年投资，运行成本;F2为DG的发电费用

（1）可再生能源的年投资成本和运行费用表达式为：

式中：n为规划年限;r为固定的年利率;C 为第i个节点处可再生能源的投资成本;C 为可再生能源的运行成本;P 为可再生能源在i节点安装的容量;xi为是否安装可再生能源;Nd为装置可再生能源的节点数目。

（2）DG的發电费用表达式为：

式中：Tmax为最大电网利用小时数;C 为第i个可再生能源的单位容量发电价格。

（3）网损费用的表达式为：

Ce为销售电价，Ploss为网损值

1.4.2 约束条件

（1）潮流平衡约束

式中：N为总节点数;Pi、Qi分别为注入到节点i的有功、无功功率;θ、f分别为节点电压的实、虚部分量;Gij，Bij分别为节点导纳矩阵的实、虚分量。

（2）节点电压约束

式中：Uimin，Uimax分别为节点i处电压的下限、上限。

（3）分布式能源接入容量的约束

式中：Pi为节点i允许安装的可再生能源最大容量。

（4）可再生能源安装总容量限制

式中：β为0.6;P为系统负荷总容量， 为高比例可再生能源率

1.5 下层规划模型

根据上述影响网损因素的分析，结合文献xx构建以下模型，重构电网结构：

1）潮流计算收敛性约束

潮流计算时，收敛性受网络结构、带入初值确定等诸多因素影响。本文计算时若迭代计算不超过40次可以收敛的方案即视为符合要求的构造方案。

2）电压幅值约束

即如式中所示，节点电压（U ）要在电压幅值最小值（Umin）与最大值之间（U ）。

3）输送线路容量约束

式中，S 为线路的最大输送容量。

4）分布式电源渗透率约束

式中，S 代表分布式电源额定功率;SL代表电网的总负荷。

应用文献【9】表示配电网的网络构架矩阵：

1）配电网不同层网络结构的线路信息矩阵C

2）包含线路首末两端节点信息的矩阵S和M

3）配电网各个层次之间的关系矩阵G

确定这几个矩阵后，把恒功率模型分布可再生能源和储能装置并入节点，即可进行对电网的前推回代潮流计算。

2 模型求解

2.1 场景削减法

分布式电源特别是光伏发电与风力发电通常有不确定性与随机性的特征，并且大部分时间的输出功率达不到额定值。如果不去考虑时间特性，只是把分布式电源作为恒定的直流点源，不同类型的分布式电源输出特性并不能完全反映，因此求出配电网的优化结果一定与实际相差甚远。所以，风电和光伏等分布式电源在接入配电网时，需要考虑电源时序特性。具体来说，像风力发电，风速会随着季节变化并存在巨大差异，能够通过待规划区域风速随着时间的变化数据得出出力特性;像光伏发电，光照强度受到天气和季节的双重影响，在进行时间划分的基础上，能够同时依据天气情况进行划分。

可以发现，分布式电源出力是以年为周期的，如果将风速、光照强度与数据样本的时间间隔设定为1小时，那一年有8760个数据样本，共8760个场景，而在模型的求解过程当中，还要对每个场景做计算，如此将导致运算量特别大，规划复杂度也高，对此运用场景削减方法减少不确定性场景个数是必要的。本文提到了改进后的K-means聚类算法来聚类类似的场景，场景聚类后，能够简化原始数据，大大缩减计算量和计算时间。对风速和光照强度聚类之后，相应的功率输出能够依据前文所描述的建模方法计算求得。

改进后的K-means聚类方法

K-means聚类算法以与k个聚类中心距离最小为原则，把数据集经过迭代分为不同的聚类，在给定聚类个数时能够得到较好的性能。但是，传统的聚类算法无法给出最优的聚类数目，在实际使用时的结果或许并不是最适合的。针对这个问题，本文依据选择聚类有效性指标，对传统的k均值聚类算法进行了一定的改进，即在聚类数目的范围内，对聚类结果进行了分析，确定下来最优聚类数目。

改进K-means方法的原理为，在聚类个数的搜索范围之内，根据聚类有效性指标来评价聚类结果质量，搜索聚类空间能够得出一系列的聚类结果，选择最优聚类结果相对应的最优聚类个数。聚类个数搜索范围为2， 中的整数，其中N是数据集中的样本总数。本文选择适合K-means聚类的Calinski Harabasz（CH+）有效性指标进行判断，CH+指数的定义是：

其中，Tk与Pk分别是k处的类间方差与类内方差，分别反映类间分散性与紧密性。随着k值的增加，Pk逐渐减少，Tk逐渐增加，而CH+的索引值在一定k时可能达到最大值，这与最优聚类数k相对应，由此应该选择CH+指数大、类数少的聚类结果。

改进后k均值聚类的算法步骤如下：

（1）设置聚类数k搜索范围为2， ;

（2）依据搜索范围内最大和最小距离原则，选择初始聚类的中心。采用k均值聚类算法对聚类中心做更新，直到能符合判别函数并收敛为止。依据聚类结果计算CH+指数，循环进行第2步;

（3）比较不同k值下的CH+指数，当CH+指数到最大值时，对应的k值为最佳簇数;

（4）输出最优聚类结果。

2.2 运用改进遗传算法进行重构[10]

该算法应采用十进制编码方法，将配电网中的回路数视为染色体长度。将环网中各开关的开、关状态视为一个复合染色体组基因，分布式供能和储能装置等效为“负”负荷，根据配电网结构独特的层次性特点，以分层前推回代来潮流解。

3 结论

本文以经济投资成本为主要目标，综合考虑可再生能源接入影响能、源规划模型以及环保节能效益等因素，实现分层分区，统筹合理分配，实现了经济效益最大化。运用场景削减法，将不确定的可再生能源出力变换为可确定的求解值。通过基于改进遗传算法进行含分布式可再生能源和储能装置的配电网重构，在保证节点电压的同时，实现了电网网损的降低，并使节点电压得到补充。本文在考虑经济效益与节能环保的同时，切实考虑电力系统安全性和稳定性的需求，使课题研究更加贴合实际需求。

参考文献

[1]吴雄.分布式电源并网多目标规划与决策研究[D].

[2]刘君.基于分类概率多场景分析的分布式电源规划研究[D].

[3]马明.分布式电源对配电网网损影响及配置的研究[D].南京理工大学，2007.

[4]涂有庆.含分布式发电的配电网网损研究[D].湖南大学，2008.

[5]司传涛，肖静，张阁，et al.光伏发电系统无功支撑能力评估分析[J].广西电力， 2015， v.38;No.156（06）：32-38.

[6]司传涛，肖静，张阁，et al.光伏发电系统无功支撑能力评估分析[J].广西电力， 2015， v.38;No.156（06）：32-38.

[7]晁阳.并网光伏发电系统无功电压控制研究[D].重庆大学.

[8]司传涛，肖静，张阁，et al.光伏发电系统无功支撑能力评估分析[J].广西电力，2015， v.38;No.156（06）：32-38.

[9]江卓翰，何禹清，曹丽璐，et al.基于改进遗传算法的含分布式电源和储能装置配电系统网络重构[J].电力系统保护与控制，2018.

[10]雷英杰，张善文.MATLAB遗传算法工具箱及应用[M].西安电子科技大学出版社，2014.