例谈教学中的“圈养”和“散养”

张仁进，江苏省南京市鼓楼区教师发展中心小学研训部副主任，高级教师。先后主持了“小学数学课堂中先研后教的范式”“小学数学建构按需乐学、大空间下的学与教动态平衡”等省市规划课题并顺利结题;多次参加市区教学基本功比赛并获一等奖，曾获南京市课堂教学竞赛一等奖，开办区级以上学术讲座五十余次，已发表或获奖的论文、案例近60篇。

[摘   要]长期以来，教师在课堂教学中一直朝着流畅、细腻、精致的方向努力，也的确创造了很多精彩的设计。然而在更关注“学”，更关注个别化发展，更关注学生综合能力提升的当下，教师应努力使教学从“圈养”走向“散养”，使核心素养的培养真正落地。

[关键词]圈养;散养;素养;小学数学

“圈养”本是一个畜牧业名词，意为关在圈里饲养;“散养”则是指在圈外分散饲养或放养。对人类来讲，虽然散养动物更健康、营养价值更高，但圈养动物产量更高、更方便。在课堂上，也存在大量类似“圈养”的教学。比如，很多教师更多地追求教学中行云流水般的过程、细腻精致的手法、令人惊艳的预设等，于是课堂该有的样子在课前就已经被严格而详细地设定好，只要按照既定“剧本”一环接一环地有序推进，就能热热闹闹而又顺利地完成教学目标。但很多学习过程也因为教师“无微不至”的精细化处理或铺垫而失去了应有的挑战性，这样的教学就如同“圈养”。

我国台湾语文教育专家李玉贵曾说：“我在大陆上课很紧张，因为这里见不得冷场。”也有其他台湾教师表达过类似的感慨，如“大陆的教师太会教了”“大陆的课堂是不是一定要教出点东西来才罢休”[1]。的确，我们的很多教学还在某种程度上“执着于教”，教师在课堂上的急功近利依然或多或少地存在，有更多刻意圈养的意味，缺少自由散养的信心。在此，将以苏教版五年级数学“除数是小数的除法”一课为例，介绍笔者的两次教学设计，解读教学中的“圈养”与“散养”。

一、第一次教学设计：“圈养”举例

1.让学生在具体情境中初步感悟算理

一是先独立思考再交流。在教学“除数是小数的除法”一课时，教师让学生先独立思考，然后再小组交流以下问题。

（1）用手机发短信0.1元一条。口答：1.5元可以发多少条短信？请列出算式并简要地写出你是怎么想的。

（2）用彩绳制作中国结，每0.25米可制作一个。现有0.75米的彩绳，可以制作多少个中国结？请列出算式并简要地写出你是怎么想的。

二是全班分享。教师在学生展示列式时强调其数量关系式，在学生叙述算法时强调两种方法：一种是化成小单位“角”或“厘米”计算;另一种是利用商不变的性质，除数、被除数同时乘10或100后再计算。

三是比较提升。引导学生比一比两题的算式与以前学过的有何不同，然后教师揭示并板书本课的课题“除数是小数的除法”。让学生比较计算每一题的两种方法有何共同点，如“都是转化成整数来计算的”，教师再板书“转化成整数”。

四是巩固算法。教师请学生口算以下题目：0.8÷0.4=（）;0.36÷0.06=（）;0.125÷0.025=（）。

五是反思总结。教师请学生谈一谈“除数是小数的除法应如何计算”。

2.让学生在对比反思中进一步明晰算法

教师先出示一个数学问题：一只鸭重2.696千克，一只鸡重0.8千克，鸭的质量是鸡的多少倍？然后用下列步骤引导学生对比和反思，明晰算法。

一是独立思考。思考：这个问题中的列式要怎样转化而商不变？只写出过程即可（见图1）。

二是组内交流。请学生在小组内观察并讨论：观察组内每人转化得对不对，如果发现有错误的，在组内开展互助，纠正错误;如果同组内出现了不同形式的正确转化，讨论哪一种转化更好。

三是全班展示分享。先判断哪些转化正确，再比较哪种转化更好。如图1的三种转化（其中包括错误示例）。

四是回顾反思。请学生再谈一谈对“除数是小数的除法”有什么新的认识。为了使学生进一步明确小数点移动的位数取决于什么，让他们再试着说一说以下各题应如何转化。

0.035÷0.05=（ ）;0.0024÷0.006=（ ）;2.6÷2=（ ）;7.98÷4.2=（ ）

显然，在以上主体设计中不乏闪光点。如层次清晰，教学环节整体上比较简约;重视激活学生生活经验，试图为学生找到理解新知的附着点;重视学习方式，努力实现教师课堂的“让、等、退、隐”等。但仔细琢磨整个教学过程，仍不难发现其中“圈養”的痕迹。

二、分析第一次教学中的“圈养”

1.与儿童天性不相适的封闭性

在拉丁文中，“儿童”一词意味着自由。蒙台梭利认为“儿童是上帝派来的密探”。苏霍姆林斯基认定儿童是探究者。探究的天性使儿童产生对周围世界的惊异，因而儿童是哲学家。好奇心、自由自在、探究未知是儿童的天性。而圈养之所以被称为“圈养”，是因为它限定了范围，限制了自由。在当下的课堂教学中，可以清晰地看到很多“圈养”的痕迹。如上例中，教师在让学生感知算理的环节，从具体情境到最后口算巩固，除数、被除数的小数位数都是相同的，显然教师的教学目标就是想先把学生“圈”在“转化成整数”这个阶段。

2.与学习过程不匹配的切割感

在圈养条件下，无论圈中动物的饭量大小，是否饥渴难忍，进食的时机都不能像散养那样自由，而是要由饲养者统一掌控，定点定时地喂食。在教学中，这一特点体现为刻意的强化与分割。上例中，教师在其创设的两个问题情境中都孕育了小数除法的算理和算法，再通过全班分享、提升概括环节，让学生初步掌握了小数除法的计算方法——移动小数点，将被除数、除数全部转化成整数。不仅如此，教师最后还通过三道口算题巩固算法、强化认识，以使学生形成更强的思维定势，即“要将除数、被除数统统转化成整数”。从某种角度来讲，这种强化具有一定的“诱骗性”。在第二个让学生明晰算法的环节，教师将重点放在了“纠偏”上（也是一种深化）：转化时不一定要将除数、被除数统统转化成整数，只需要按照商不变的规律将除数转化成整数即可。而这个“偏”的原因正是上一阶段“喂食”的结果。这样，对于“除数是小数的除法”的计算法则，学生经历了两个阶段才完成。

事实上，从学习者的角度思量，学习的过程应该是一个连贯的过程，但并非所有学生都必须经历这样的过程。少数学生可能在课前已经知晓算法，大多数学生在这些学生的启发或引领下完全可以自己理解并掌握，个别“学困生”只要花些时间也完全能够“跟上来”。更重要的是，这段跋涉的过程无论对哪种水平的学生来说，都是一次可贵的“学习之旅”。然而，教师因为怕学生出错，怕课堂乱，怕课堂生涩冷清不热闹，将一个连贯的学习过程人为地分割成了两个环节，将学习目标封顶，不许学生越雷池一步。

3.与儿童发展相背离的温室效应

被圈養的动物虽然生活空间封闭，但是有固定的场所遮风挡雨，有人定时投喂，久而久之，它们的天性或求生能力就会退化，一旦开圈放生，在自然界将难以生存。教学中的“圈养”也同样如此。学习是一个连贯的过程，任何一个问题的解决、概念的建构、技能的形成都必须经过学习者的入境、联结、建构、重组才能实现。但是，教师因为要“分散难点”“稳步分层推进”，便将一个相对完整的教学活动过程人为地转化成若干“小步走”，这往往能使课堂显得非常紧凑、热闹、好看，学生也因为“小步走”而觉得数学不难，生活不难。然而同样的知识，当教师以更接近现实情况的数学问题考查学生时，就会发现原来课堂上的“高歌猛进”只是虚假繁荣。这正是因为学生平时“圈养”得过多，完整经历问题解决的过程少，全历程的数学活动体验少，在解决实际问题过程中的碰壁、调整、反思、重建的过程不明显造成的。为了使教学能够突破这种“圈养”，笔者改进了教学设计。

三、第二次教学设计：“散养”探索

1.引出问题

教师出示例题：妈妈买鸡蛋用去7.98元，每千克4.2元，妈妈买了多少千克鸡蛋？要求学生说明“妈妈买了多少千克鸡蛋”怎样列式以及自己是怎样想的。过程如下。

教师板书关系式：总价÷单价=数量

师：估算一下，这道题的商大约是多少？

生：把7.98看成8，4.2看成4，商大约是2。

2.探究算法

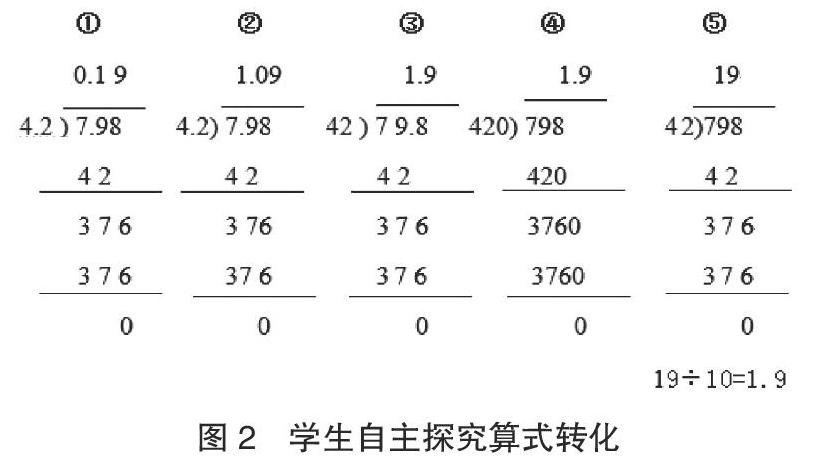
一是自主探究“7.98÷4.2”。教师给出研究提示：用以前学过的知识在学习单上算出来，并在小组内交流自己的想法。尝试计算并展示不同的解法，说一说每种算法的思路是什么（见图2）。

二是全班交流。请学生判断：哪些算法是错误的？为什么？学生A说：估算的时候大约是2，所以不可能是0.19和1.09。学生B说：第一种7.98大于4.2，商应该大于1。学生C说：4.2×（）=7.98，商一定是一个一位小数，不可能是1.09。接下来是请计算正确的学生介绍经验，说一说自己的算法思路。以下是学生的几种回答。

（1）把除数和被除数同时乘10变成79.8÷42计算，或者把7.98元和4.2元换算成“角”计算（79.8角和42角）。

（2）把除数和被除数同时乘100变成798÷420计算，或者把7.98元和4.2元换算成“分”计算（798分和420分）。

（3）把除数乘10，被除数乘100，最后的商再除以10变成1.9。

三是理性思考。教师引导学生：先回味每一种算法，再静静思考，你比较欣赏哪一种算法，为什么？必要时可以举例说明你的观点。这里是希望通过学生之间的互动与交锋，使争论的话题聚焦在小数点移动的位数。如果学生触及不到这一话题，教师可以提问：是不是一定要把除数、被除数全部转化成整数？举例说明。这样，学生的举例中必定会有类似于“2.916÷1.2”这样的算式，这会让学生进一步在竖式计算中体验“移动小数点取决于除数的简便性”。

四是比较抽象算法。请学生根据刚才几道题目的计算，谈一谈它们在算法上有什么共同点。学生提出：都是把除数转化成整数。教师完成板书“除数是小数→除数是整数”。

四、分析第二次教学中的“散养”

以上两次教学中，教学二基本保留了教学一的优点，同时较好地解决了教学一中的不足，隐约可见“散养”的意味。具体体现在以下几个方面。

1.放手创设大空间让学生自主尝试

突破“圈养”的明显标志就是要给学生足够大而可行的活动区域。因为学生已有“除数是整数的小数除法”的计算经验，因此在教学二的开始，教师开门见山，比教学一少了两个情境，这样便于学生在黄金时间内集中精力解决主要问题。教学二通过减少两个情境而拆除了不必要的框框，即没有了教学一中过度的预设，使学生能直面更真实的问题，因而学生可以信马由缰，使解决问题的过程更加完整，学习也更具连贯性。

2.突出了个体自主建构的全过程

长期以来，受传统教学观念的影响，课堂更多呈现的是“全体”——基于集体的教学，因而往往求同明显，求异不足。个别化、个性化学习容易被忽视。教学二基于“散养”的理念，为突破以上局限做了一定的尝试和努力。在课堂开始的自主尝试环节，显然每一个学生都在积极回忆、联结、调取相关知识经验，在积极地解决问题。无论尝试正确还是错误，对学生个体来说都是一次有意义的经历。在全班分享汇报环节，学生个体之间相互推动、相互启发、相互学习，是促进每一个体实现不会到会、不明晰到明晰、不透彻到透彻的过程。在理性思考算法择优环节，巩固前面习得的计算方法，同时通过计算正确的学生举例、计算，让计算错误的学生体验到小数点移动的关键点。最后通过抽象概括出“除数是小数的计算方法”。教师希望通过这种有目的的课堂“散养”，让学生之间互相影响和推动，完成知识的自主建构。这样，学生在教学中就不仅获得了知识与技能，还有思想方法、过程体验和经验积累。

3.凸显理性思维与学习探究的主动性

数学思维说到底是一种理性思维。虽然对小学生来说，强调理性思维还为时过早，但可以结合具体学习内容渗透理性意识。如本例中，在探究算法环节的理性思考部分，教师提出“先回味每一种算法，再静静思考，你比较欣赏哪一种算法，为什么”的问题，显然就是想激发个体理性思考的意识。有的学生拘泥于自己的算法，有的学生听过同伴发言后进行了调整或吸纳了别人的算法，有的学生敏锐地发现了转化中的简便方法……接下来教师就以学生的有机生成（学生举例的算式）作为学习资源，进行二次竖式计算，这一过程对大部分学生来说是验证环节，对少数暂时有困难的学生来说是体验过程，通过计算类似于“2.916÷1.2”的算式，体验转化中的简便方法。这样，就在学生主动探究的学习中体现了理性思维。

必须指出，这里的“散养”不是自由放养，而是一种积极而富有意义的、基于明确目的的“散养”，但是这种所谓的“明确目的”是隐性的，它隐藏于数学活动之中。教师的作用应该集中体现在教学活动的预见、设计和组织，即学习场的创建和维护上，使每一名学生在这样的学习场中能够自主选择、自由奔跑、总结和反思，最大限度地突出“每一个的学习、每一个的生长”，而对学生核心素养的培育自然隐于其中。

参考文献

[1]陈洪杰.追问观点背后的观点·小学数学教师[M].上海：上海教育出版社，2017.

（责任编辑   郭向和）