基于统计分析的最优救援井数量及救援成功率研究

张 森, 刁斌斌, 高德利(中国科学院院士)

(中国石油大学石油工程教育部重点实验室)

0 引言

钻井平台一旦发生井喷、爆炸着火等事故，将不能靠近钻井平台进行作业，如果不能在短时间内完成救援封堵作业，那么将会造成严重的经济损失和环境污染。目前，救援井仍是解决这一类问题最有效的方法[1-3]。

由于救援井与事故井在地下精确连通的难度较大，一次封堵成功率比较低，现有的测距技术和连通工具很难实现救援井与事故井的一次性连通[4]。那么如何利用救援井在最短的时间内、用最低的成本和最优的救援井数量完成救援任务是救援井计划的重要组成部分。在制定救援井计划时，需要考虑两个问题：在不考虑救援成本的情况下，是否可以通过无限增加救援井的数量来缩短封堵的时间？在考虑救援成本的情况下，该如何根据现场的救援能力选择合适的救援井数量和救援井的启动时间？本文采用统计学的方法对以上问题进行详细分析。

近些年统计分析的方法在石油工程领域发挥了一定的作用[5-8]。本文结合现场实际救援能力用统计分析的方法建立了“时间-累积封堵成功率”模型，该模型在考虑人力资源、基础设备和关键技术等条件的情况下，系统分析了尝试封堵的次数、连通工具的性能(封堵成功率)、平均钻井时间、救援井数量、救援井的启动时间对累积封堵成功率的影响，并且通过实例验证该模型的实用性，为在不同的事故类型和救援能力的情况下制定出最优的救援井方案提供一定的理论支持。

1 “时间-累积封堵成功率”模型的建立

1.1 骰子游戏

“骰子游戏”的游戏规则：首先，取一个常规的六面体骰子，重复的滚动骰子直到出现6点，记录所需要滚动的次数n，记为一组游戏。按照这样的规则进行足够多组游戏后，统计出n所对应的出现6点的频率f，频率f除以总的滚动数N得到n所对应的出现6点的概率，从游戏看出，滚动1次就出现6点的概率最大，随着需要滚动次数的增加出现6点的概率逐渐减小。

以上游戏记录的是出现6点的次数，现在记录骰子出现6点时所用的时间。一次拾骰子和掷骰子记作一个回合，假设每一个回合的时间相等，记为一个平均时间ta。如果某一组游戏中用了3个回合，那么这一组游戏的时间记3ta，可以看出随着滚动回合的增加，一组游戏时间也会增加。如果将出现6点的概率比作封堵成功的概率，将滚动的次数比作尝试封堵的次数，通过将次数转化为时间的方式就可以得出时间与封堵成功率的关系。

1.2 “时间-累积封堵成功率”模型

假设：该模型中救援井到达事故井附近后成功连通并且封堵的概率为Ps，如果第一次连通失败，将钻头上提，填埋钻孔，进行新一轮的尝试，再次尝试的情况下，救援井由于卡钻等自身的原因导致救援井失效的概率记为Pu。这里采用正态(高斯)分布N(μ，σ2)来统计救援井到达事故井附近所用时间的累积概率分布[9-11]。由正态分布的定义可知：

时间的概率密度分布表示为：

(1)

时间的概率密度分布的积分是累积概率分布，可表示为：

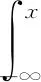
(2)

从而可以得出时间与累积封堵成功率的关系：

P=Ps·FX(x)

(3)

式中:fX(x)—概率密度函数;

FX(x)—累积分布函数;

P—累积封堵成功率;

μ—平均值;

σ是标准差。

多次尝试必然导致作业时间的延长，这里采用具有单独均值和标准差的高斯分布描述这个时间延迟，这种方法在数学上描述为初始时间分布与对应于的第二分布的卷积[12-13]。计算方法如下：

由式(3)可知第一次尝试的累积封堵成功率：

P1=Ps·Gaussian(t1,SD1)

(4)

每次尝试失败后，开始新的尝试时将产生一个新的高斯，新的尝试将会产生额外的时间，那么在第i次尝试时，时间与累积封堵成功率之间的关系：

Pia=Pi·Gaussian(t2,SD2)×Gaussian(ti-1,SDi-1)

(5)

缩放因子Pi可表示为：

(6)

由于高斯的卷积特性，新高斯的标准差表示为：

(7)

式中:Pia—第i次的累积封堵成功率;

Gaussian()—给定平均时间t和标准差SD的高斯分布;

Pi—缩放因子。

假设：每一口救援井到达事故井的平均时间t1=60 d，标准差SD1=5 d，封堵成功率Ps=25%，那么一次尝试的情况下到达事故井附近的时间密度概率和累积封堵成功率的分布如图1所示。

图1 一次尝试封堵的时间密度概率和累积封堵成功率

由图1可知，在一次尝试封堵的情况下，由累积封堵成功率曲线可以看出要达到25%的封堵成功率大约需要75 d。当到达最大封堵成功率后，随着时间的延长封堵成功率不会再增大。可见，在给定封堵成功率的条件下，75 d内完成封堵的概率只有25%，这远远不能保证在规定时间内完成有效封堵。

2 救援井数及启动时间对累计封堵成功率的影响

尝试封堵次数对累积封堵成功率的影响，假设：现场的救援条件只能满足1口救援井的施工，现场的救援参数如表1所示。

表1 现场设计的平均时间和标准差参数

2.1 救援井数量n对累积封堵成功率的影响

单个救援井很难同时满足作业时间短和封堵成功率高的两个条件。所以基于多个骰子的“骰子游戏”的情况下建立了“时间-累积封堵成功率”模型，假设该模型中每个救援井的累积成功概率分布是相同的，且每口救援井之间不会互相干扰。

当同时钻n口救援井时，时间与累积封堵成功率的关系表现形式如式(8)：

(8)

式中:CPD—累积封堵成功率。

分析当同时钻2口、3口和4口救援井时，时间和累积封堵成功概率的分布如图2所示。

从图2可以得到：①通过增加同时启动的救援井个数可以增大最大累积封堵成功率，但到达最大成功率的时间不同，井数越多用时越少；②1口井到达80%的概率需要大约119 d，同时启动2口、3口和4口救援井到达理想成功率的时间分别约为：84 d、74 d和70 d；③增加同时启动的救援井数量可以缩短到达理想累积成功率的时间，但随着井数的增加，缩短到达理想成功率时间的效果呈递减趋势。

2.2 救援井的启动时间对累积封堵成功率的影响

假设每口井的推迟时间都是相对于第1口井而言，将第2口救援井的启动时间分别设置为+15 d、+25 d和+35 d(+代表推迟)。第2口井的启动时间设定为+20 d，第3口井的启动时间分别设置为+30 d、+40 d和+50 d。

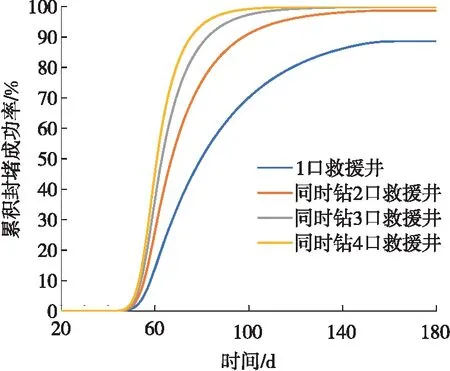
图2 多口救援井同时启动时的累积封堵成功率

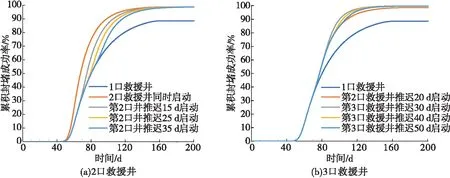
图3 救援井的启动时间对累积封堵成功率的影响

从图3(a)可以看出：相对于1口救援井而言，第2口救援井启动的推迟时间越长其到达理想累积封堵成功率的时间越长。从图3(b)可以看出：当第2口井的启动时间一定时，第3口井到达累积封堵成功率的时间会随着启动时间的推迟而延长，但对到达理想成功率的时间影响不大。

3 案例分析

2010年4月墨西哥湾“深水地平线”钻井平台爆炸事故，对人类造成了巨大的经济损失，对环境造成了严重的污染[14-16]。将参数代入“时间-累积封堵成功率”模型中计算分析，可以得到时间与累积封堵成功率的关系,如图4所示。

从图4中可以看出：相对于1口救援井，第2口救援井推迟18 d启动仍然可以明显缩短到达理想累积封堵成功率的时间；第3口救援井和第4口救援井在推迟50 d启动的情况下与第2口井推迟18 d启动所达到理想累积封堵成功率的时间相差不大，在预期的时间内采用2口救援井就可以到达累积封堵成功率，这时启动第3口救援井或者第4口救援井并不能缩短到达理想成功率的时间。所以BP公司采用了2口救援井的方案，从而验证的该模型的实用性。

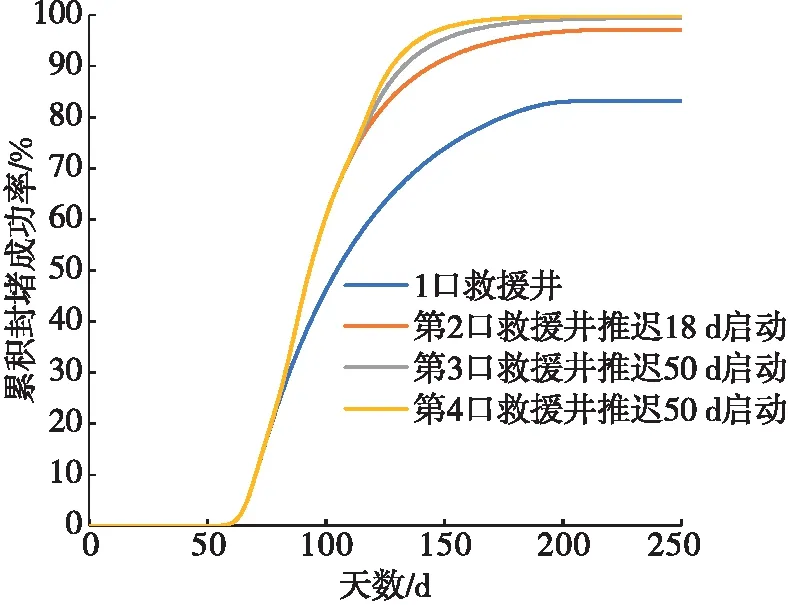
图4 “深水地平线”的累积封堵成功率

4 结论

1)“时间-累积封堵成功率”分析表明，利用1口井救援井进行一次封堵成功率较小，目前只能通过采用多次尝试封堵的方法可以提高累积封堵成功率，但会延长达到理想封堵成功率的作业时间。

2)“时间-累积封堵成功率”显示，相对于1口救援井而言，多口救援井作业可以缩短作业时间、提高最大累积封堵成功率。但是每口救援井的启动时间对累积封堵成功率有一定的影响。在同时启动多口救援井的情况下，井数越多到达理想累积封堵成功率的时间越短。随着井数的增加，缩短到达理想成功率时间的效果呈递减趋势。在不同时启动多口救援井的情况下，每口井的启动时间的间隔越短到达理想成功率的时间越短。但是当后1口井的启动时间推迟到一定的期限时，增加救援井的数量将不能显著缩短到达理想累积封堵成功率的时间。

3)在实际处理事故中，救援井数量和启动时间会受实际救援条件的限制，结合现场的人力资源、基础设备和关键技术等条件，“时间-累积封堵成功率”模型可以制定出一套合理的救援井方案。