基于最小延迟时间的宽频带柔性罗氏线圈设计研究

张 石，姜 奎，张 博，夏 晖，孙 通，霍焕杰，许益纬，朱 博

（1.龙源（北京）风电工程技术有限公司，北京 100034；2.合肥工业大学 电气与自动化工程学院，安徽 合肥 230009）

0 引 言

近年来，智能电网的大力建设对电力系统的在线监测水平提出了更高要求。作为电力系统状态监测信息获取的主要手段，柔性罗氏线圈因为具有不含铁芯、无铁磁饱和问题、频带宽以及便于实现开口设计等显著优点，在电能质量监测和瞬态电流测量等领域中得到广泛应用[1-3]。

柔性罗氏线圈由于其无铁芯设计，也带来了增益较低和信噪比差的问题，因此需要将线圈本体的输出信号送至有源积分电路，提升输出信号的信噪比。相较带铁芯设计的自积分线圈和无源积分线圈，有源积分罗氏线圈积分电路和线圈本体结构参数选择较为复杂[4-8]。传统的设计方法需要多次调整结构参数才能达到预期的性能指标。为提高设计效率，本文提出依据现场使用环境，在给定部分结构参数情况下，基于延迟时间最小原则的宽频带柔性罗氏线圈参数设计方法[9]。

文中介绍了有源积分罗氏线圈的基本原理，基于集总参数模型分析了有源积分罗氏线圈的传递函数，最后提出了一种宽频带柔性罗氏线圈参数设计方法。设计并制作了脉冲电流测试线圈，通过试验测试验证了设计方法的可行性。

1 罗氏线圈测量原理

罗氏线圈测量电流的基本原理为法拉第电磁感应定律。如图1所示，载流导体穿过圆环形罗氏线圈的中心，并与罗氏线圈平面垂直[10]。

图1 罗氏线圈测量原理示意图

假设载流导体中流过的被测电流为i(t)，根据安培环路定律，有：

式中，H为磁场强度，l为线圈的周长，B为磁感应强度，μ0为真空磁导率。

对于圆环型罗氏线圈，可进一步推导得到：

式中，rc是线圈中心半径。

设线圈输出的感应电动势为e(t)，线圈匝数为n，每匝线圈截面面积为A，则有：

可见，罗氏线圈的感应电势e(t)正比于被测电流的变化率。要得到被测电流的波形，还需要根据被测电流的特点，设计积分电路进行还原处理。

2 宽频柔性罗氏线圈传递函数分析

柔性罗氏线圈为无铁芯设计，磁导率小，无源积分电路积分效果与信噪比不能兼顾，这导致其理论频带参数往往无法兼顾低频与高频性能。文中采用文献[11]提出的线圈自积分、无源积分以及有源积分电路配合的复合积分电路设计方案来解决此问题，该方案可将工作频带拓宽到谐振频率。所采用的罗氏线圈传感器复合积分电路如图2所示。

图2 复合积分电路设计图

对于上述罗氏线圈测量电路，线圈部分由基尔霍夫定律有：

联立式（4）～式（6），得到线圈部分有：

对（7）进行拉氏变换，得到其传递函数H0(s)为：

无源积分器与有源积分器传递函数分别为：

整体传递函数为：

式中，I(s)为被测电流的拉式变换；M为互感系数；Rs为线圈内阻；L为线圈自感；C为线圈等效电容；Ra为终端电阻，用于实现自积分；u0(·)为积分器输出电压；R1、C1为无源积分电阻和电容；R2、R3、C2为有源积分电阻和电容。

上述复合积分电路的罗氏线圈传递函数中，传感器的增益与互感系数、延迟时间、积分电阻以及积分电容有关。整体的高频特性受线圈的自感L与线圈等效电容C的乘积（延迟时间）限制，乘积越小，线圈的高频特性越好[11]。因此，文中在设计线圈参数时，重点关注线圈的工作频带，设计线圈本体结构参数时，核心原则是延迟时间最小，以保证线圈的高频性能达到最优。

3 宽频罗氏线圈结构参数优化方法

典型罗氏线圈的结构如图3和图4所示，利用漆包线在一柔性材质的骨架材料上按照螺旋结构均匀绕制。在骨架材料始端绕制到末端后，从骨架材料的中心穿过一根回线回到始端，如图1所示。完成绕线后填充柔性材料，并布置屏蔽层。屏蔽层外部通常加装外部绝缘材料，起到保护传感器的作用。

图3 罗氏线圈的截面图

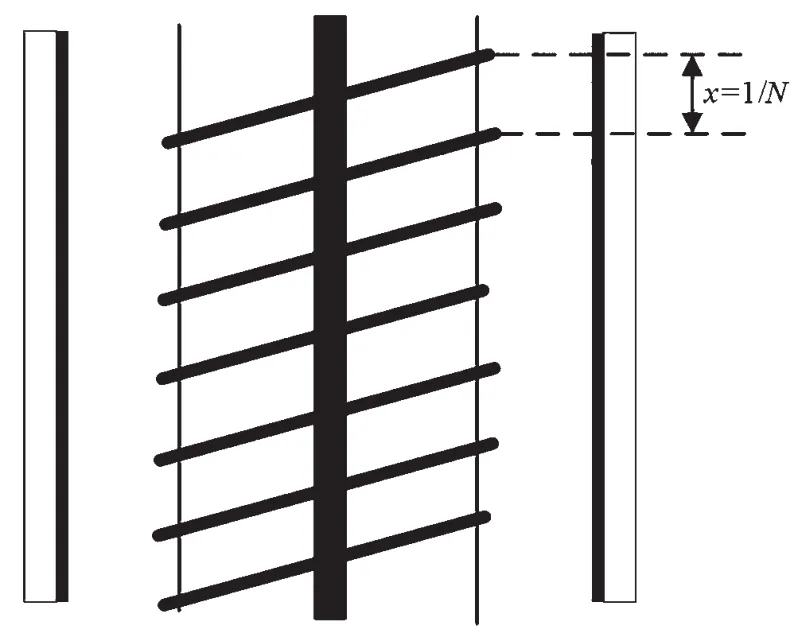
图4 罗氏线圈的绕线示意图

如上所述，传感器的高频性能与线圈自感和电容参数密切相关。影响线圈自感和电容参数的关键结构参数包括线圈周长l、屏蔽层直径ds、线径dwire、填充材料与骨架材料的相对介电常数ε1和ε2、骨架截直径df以及单位长度上线圈的匝数N（绕线密度）。

根据罗氏线圈的测量原理，互感系数M为：

线圈骨架截直径df为：

现有文献中一般采用L0=μ0N2A计算单位长度线圈的自电感，其中N=n/l，为骨架截面积。该公式仅在紧密绕制的线圈中，即x＜2.5dwire时成立，其中x=1/N。当x＞2.5dwire时，单位长度自电感L0应修正为：

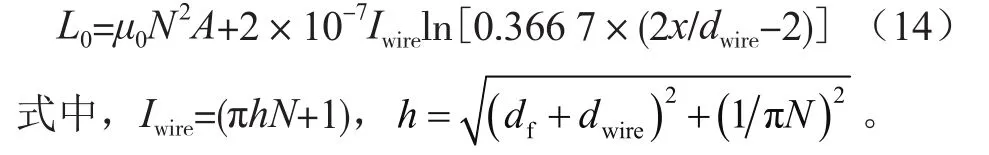
C R Hewson等人的实测数据表明，线圈单位长度电容满足：

基于上述理论，提出的线圈结构参数设计思路包括以下几个步骤。一是根据线圈布置环境的具体需求，确定线圈周长l、屏蔽层直径ds、导线直径dwire以及填充材料与骨架材料的相对介电常数。二是根据被测电流的频率与幅值，确定线圈灵敏度M，即互感系数。三是基于延迟时间最小原则，寻找绕线密度N的最优取值，使得LC最小，代入式（13），确定骨架截面直径df。四是根据变比要求及文献[10]中提出的复合积分电路时间常数的匹配关系，确定积分电阻和积分电容。

4 适用于8/20 μs雷电流测量的线圈设计与测试

针对雷电脉冲电流测试需求，本文设计了一套可用于8/20 μs雷电流测量的线圈，并开展了试验测试。

4.1 罗氏线圈结构参数设计

通过文献调研发现，雷电流脉冲上升时间一般为微秒级，电流峰值一般为kA级别。国标中规定的实验室雷击损坏相关试验中采用的标准电流波形为8/20 μs，其频率分量主要为10 kHz～1 MHz。同时，考虑到实验室脉冲电流测量对线圈长度要求不高，为此文中将设计的线圈互感系数定为100 μH。主要结构参数设定如表1所示。

表1 罗氏线圈传感器结构参数表

将上述参数代入式（14）～式（17），得到延迟时间随N的变化曲线如图5所示。由图可知，当N取5 000时，延迟时间最小，罗氏线圈的高频截止频率可达到理论值上限。考虑到被测电流的幅值一般为数千安，因此将传感器变比设置为1 V/1 kA，最大电流为10 kA。

图5 延迟时间L0C0随N的变化曲线

根据文献[10]所设计的复合积分电路，其核心思想是将无源积分和有源积分环节的工作频带进行组合，从而拓宽整体积分器的工作频带。为此，需要通过电路参数的特定设计，保证不同积分环节截止频率相互匹配。如图6所示，图中无源积分环节的截止频率为1/T0，有源积分环节的截止频率为1/TL和1/T1，通过电路参数设置，使得1/T0与1/T1相匹配。文中，TL=R3C2，T1=R2C2，T0=R1C1，ωc为线圈自然谐振角频率，基于上可以设置积分电路中的元件参数如表2所示。

图6 复合积分器幅频特性

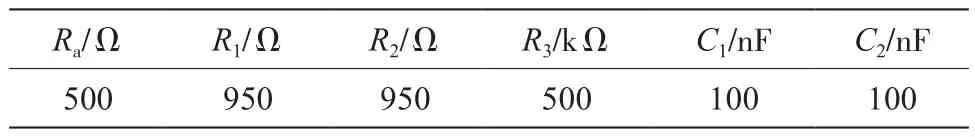
表2 复合积分器参数表

将设计的线圈参数带入罗氏线圈传递函数（11）可得，罗氏线圈与积分器整体的幅频特性如图7所示。由图可知，所设计的线圈理论频带范围为10 Hz～1 MHz，幅频特性为-60 dB，可满足雷电脉冲电流测量的频带和设计的变比需求。

图7 罗氏线圈整体的频率特性曲线

4.2 罗氏线圈性能测试试验

基于表1中的设计参数，制作了如图8所示的罗氏线圈样品，并开展了雷电冲击电流测试试验，测试获得了所设计自制宽频罗氏线圈的测量性能。测试中分别采用自制宽频罗氏线圈与Pearson110线圈同时测量回路电流。测量典型波形如图9所示，图中自制宽频罗氏线圈上升沿为6.62 μs，50%脉宽为21.08 μs，Pearson110线圈测量波形的上升沿为7.18 μs，脉宽为22.1 μs。两者上升沿时间相差不超过7.8%，50%脉宽相差不超过4.3%。图9中的波形幅值存在一定差异的原因，是由于自制线圈变比与Pearson线圈变比不同。自制线圈与Pearson线圈测量幅值的差异分析如图10所示。两者的峰值之间的线性相关系数为0.975，表明文中所设计的线圈的线性度较好。上述测试结果表明，文中设计的传感器在脉冲雷电流测量中与标准线圈测量结果基本一致，证明了文中所提出的设计方法的合理性。

图8 文中设计的罗氏线圈

图9 自制罗氏线圈与Pearson测试对比图

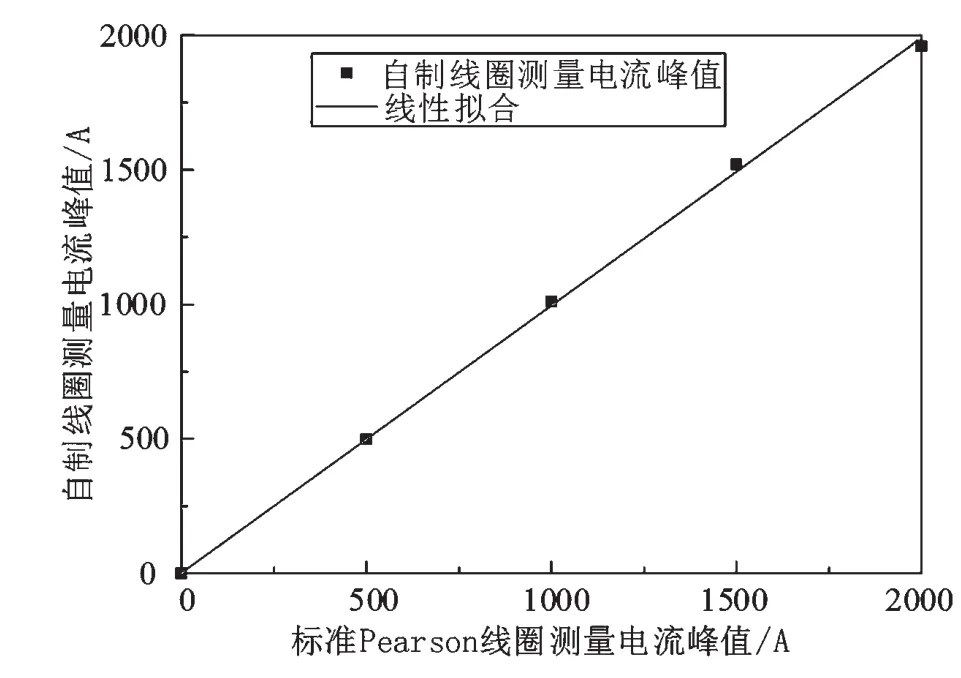
图10 自制罗氏线圈线性度测试

5 结 论

本文提出了基于延迟时间LC最小原则的宽频带柔性罗氏线圈的参数设计方法，基于该设计方法，线圈高频性能可一步达到最优。设计了一款适用于实验室脉冲雷电流测量的柔性罗氏线圈并开展了实验室测试，所设计线圈实际测量波形与Pearson线圈测量波形进行对比，性能如下。一是上升沿时间相差不超过7.8%，50%脉宽相差不超过4.3%，二是不同电流峰值下，幅值结果高度线性相关，线性相关系数为0.98。测试结果表明，所设计的线圈可以满足微秒级上升沿雷电流测量需求，即文中所提出的线圈参数设计方法具有可行性。