东海深部地层时深转换关系的分段优化拟合
陶天生,李春峰,李珂迪,姚泽伟
(浙江大学 海洋学院,浙江 舟山 316021)
0 引言
在地震资料处理和解释中,时间域地震剖面虽然可以反映构造的整体形态与位置,但不能确切地描述构造的深度和产状。因此,在精细的地质与地球物理研究中,通常需要对地震剖面进行时深转换,将地质层位从时间域转换到深度域。目前进行时深转换的方法有很多,如变层速度模型法、速度控制点法、二元回归法、井震联合速度建模法等[1-4]。不同的方法适用于不同的地质条件,但每种方法都有其局限性。拟合公式法是利用钻井获得的时深数据进行时间-深度的曲线拟合,得到时-深对应关系式。由于钻井深度的限制,获得的数据一般在5 000 m以内。对于更深部地层的时深关系,可以通过上部地层的外延来实现。
目前拟合公式法常用多项式或幂函数关系式来构建模型[5-6]。在钻井控制深度内,它们的拟合度都很高,但在没有控制点约束的深部,不同模型的外延结果往往有很大差异,且深度越大,差异越明显。针对这一问题,本文以东海陆架盆地中部某凹陷41口钻井垂直地震剖面数据(VSP)为基础,用软件构建不同的时深关系模型,获得深部地层的时深对应关系。利用三维地震勘探中获取的层速度资料计算每口井的时深对应关系,将结果和模型进行对比,探讨不同模型在深部地层时深转换的准确性,建立了研究区时深转换的分段拟合模型,提高了深部地层时深转换的准确度。
1 数据与方法
本文用到的钻井VSP数据和三维地震速度体数据均由中国海洋石油集团有限公司上海分公司提供。VSP是在地表激发地震波,在井内安置检波器接收地震波,然后经过校正、叠加、滤波等一系列处理得到深度、时间、速度数据,具有准确可靠的优点,但是钻井深度有限,无法到达深部地层。三维速度体数据是由多道地震速度谱分析获得,其优点是深度、时间、速度数据范围大,可以到达深部地层,但准确度不及钻井VSP数据。
本文统计了东海陆架盆地中部某凹陷41口钻井的VSP数据以及相应位置的三维速度体数据(图1),VSP数据的时间域范围是0~3.65 s,深度域范围是0~5 582 m(表1)。速度体数据的双程旅行时(TWT)范围是0~8 s。
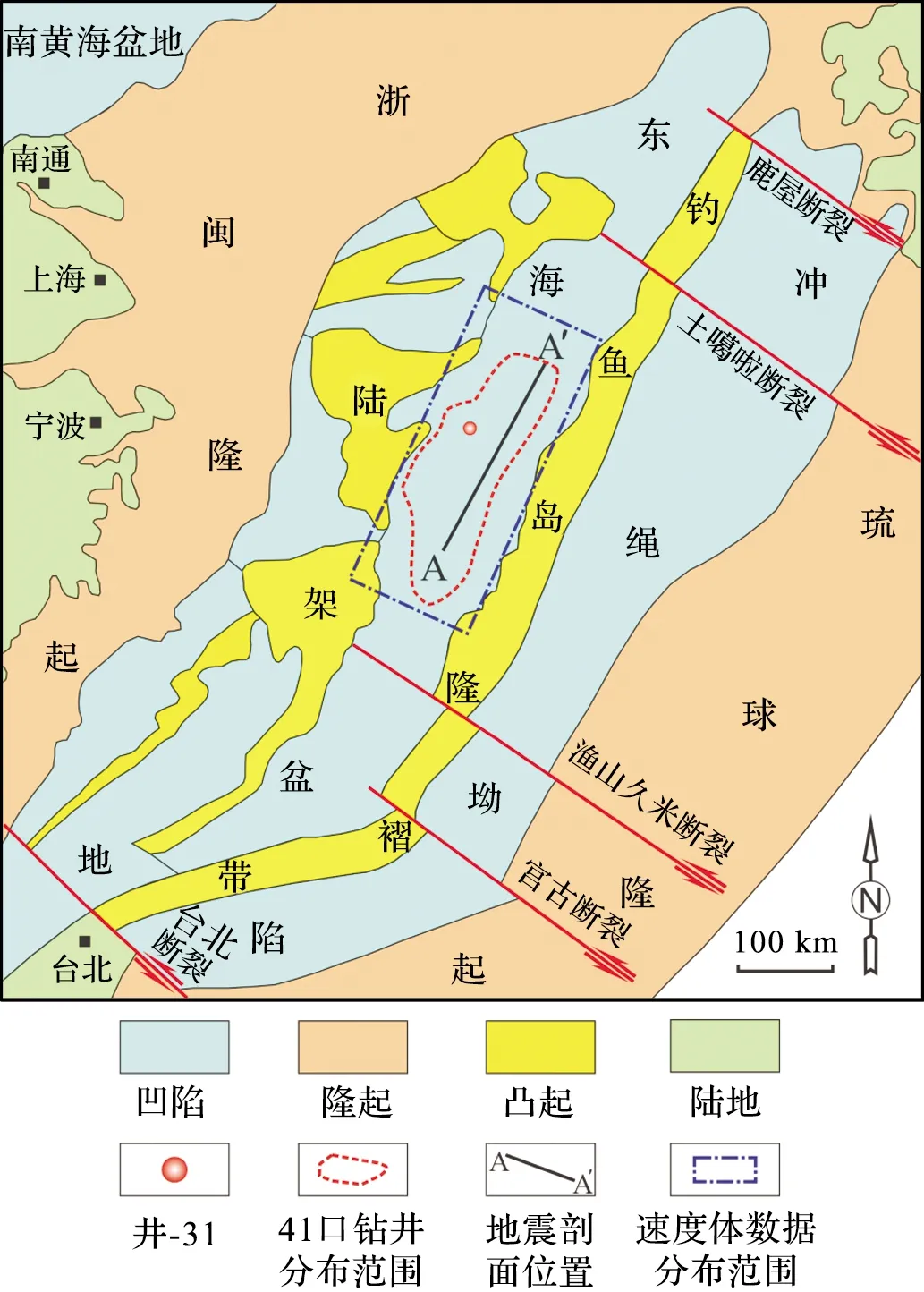
图1 东海陆架盆地构造位置图[7] Fig.1 Geodynamic framework of the East China Sea Shelf Basin[7]
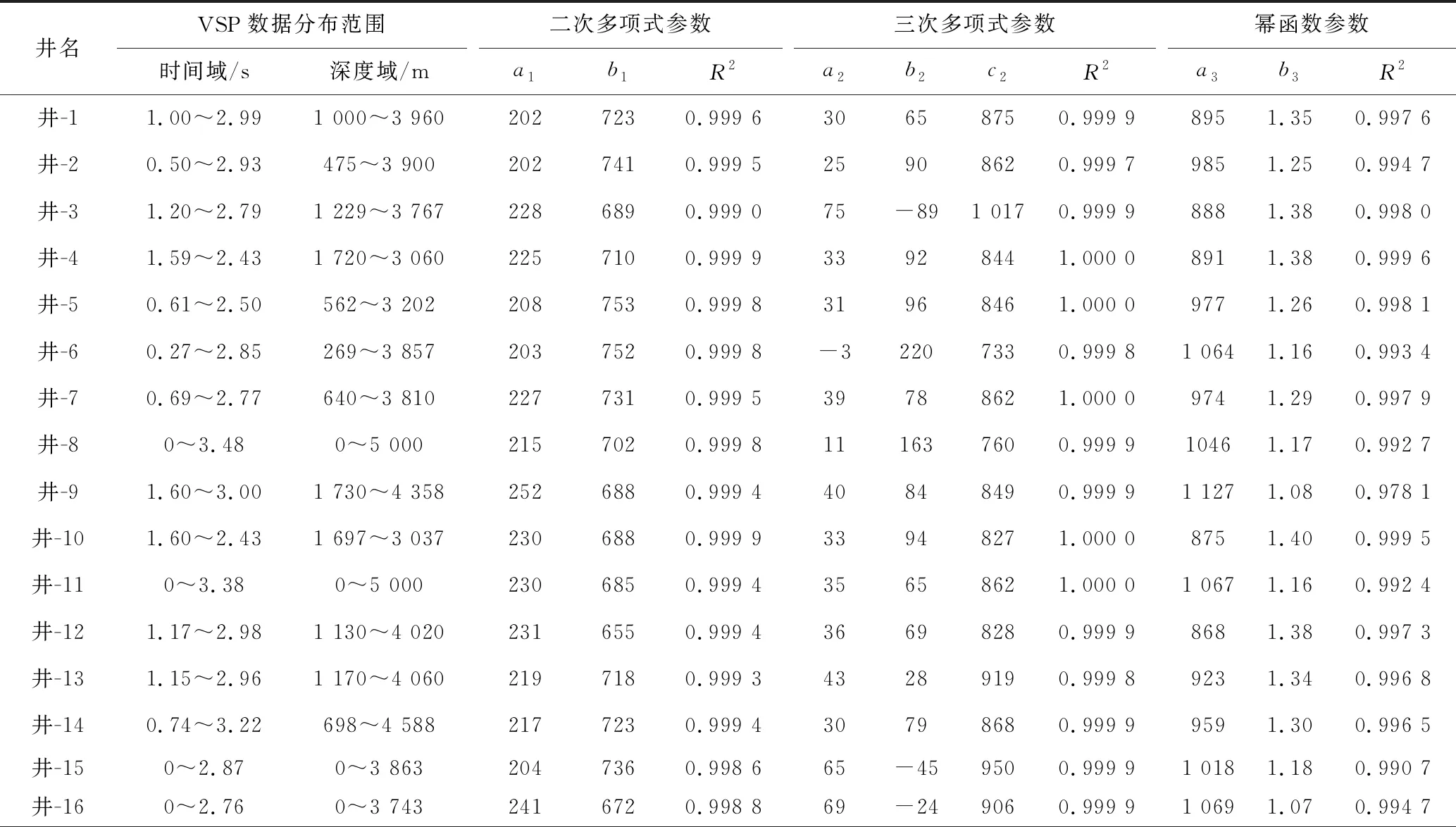
表1 41口钻井VSP数据时深分布范围与全段时深拟合公式参数Tab.1 Time and depth distribution of VSP data and fullsegment time-depth fitting parameters from 41 drilling holes

表1 (续)
在钻井控制深度内(TWT≈0~3 s),三维速度体数据与钻井VSP数据计算得到的时深点和时速点几乎重合(图2),说明三维速度体数据在浅层准确可靠。在TWT大于3 s的地层内,层速度增速随深度逐渐减慢(图3),符合一般的地质规律。在TWT=8 s 时,41口钻井位置的平均地震层速度达到6 208 m/s(图3),深度达到18 140 m(图4),与WANG et al[8]的研究结果基本一致。本研究根据三维速度体数据计算所得的研究区速度结构的变化趋势与前人在东海陆架盆地南部地区的研究结果接近[9]。另外,地震剖面AA′显示研究区的莫霍面TWT大约为11 s(图5),以速度体数据0~8 s的时速对应关系为基础,按层速度增速减慢的合理趋势外推3 s,估计8~11 s内地层平均速度为6 500 m/s,以此计算出莫霍面的深度为27 890 m,也与前人利用不同方法计算的结果基本一致[10-13]。综上,本研究认为三维速度体数据在TWT为3 s之下的深部地层是准确可靠的,以三维速度体数据的计算结果来判断不同模型在深部地层中的适用性是可行的。为了表述方便,将由速度体数据计算得到的深度和速度分别称为“实际深度”和“实际速度”。
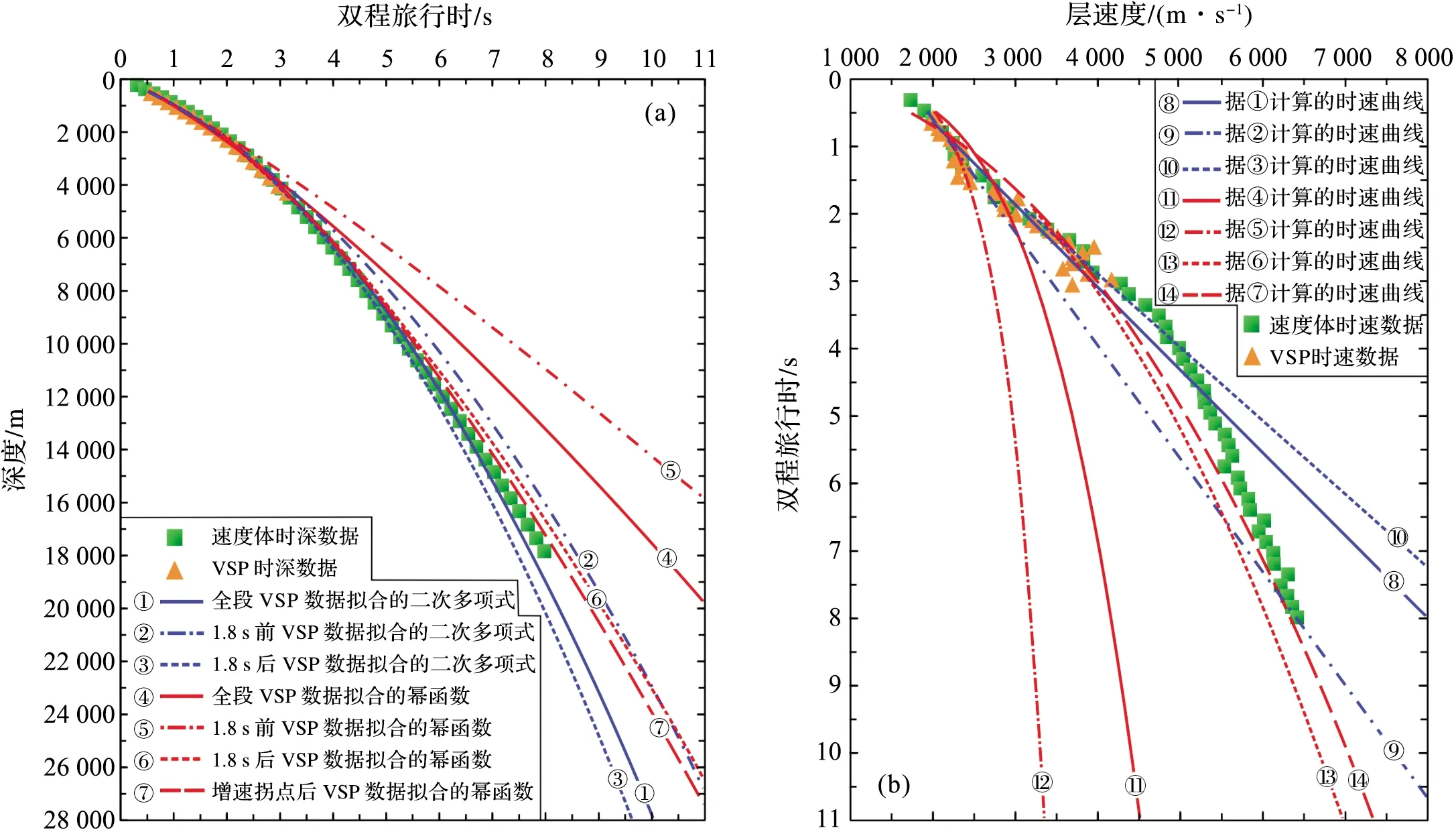
图2 井-31时深散点和拟合曲线图(a)及时速散点和计算的层速度曲线图(b)Fig.2 Time-depth scatter plot and fitting curves(a) and time-speed scatter plot and calculated interval velocity curves(b) of the well-31
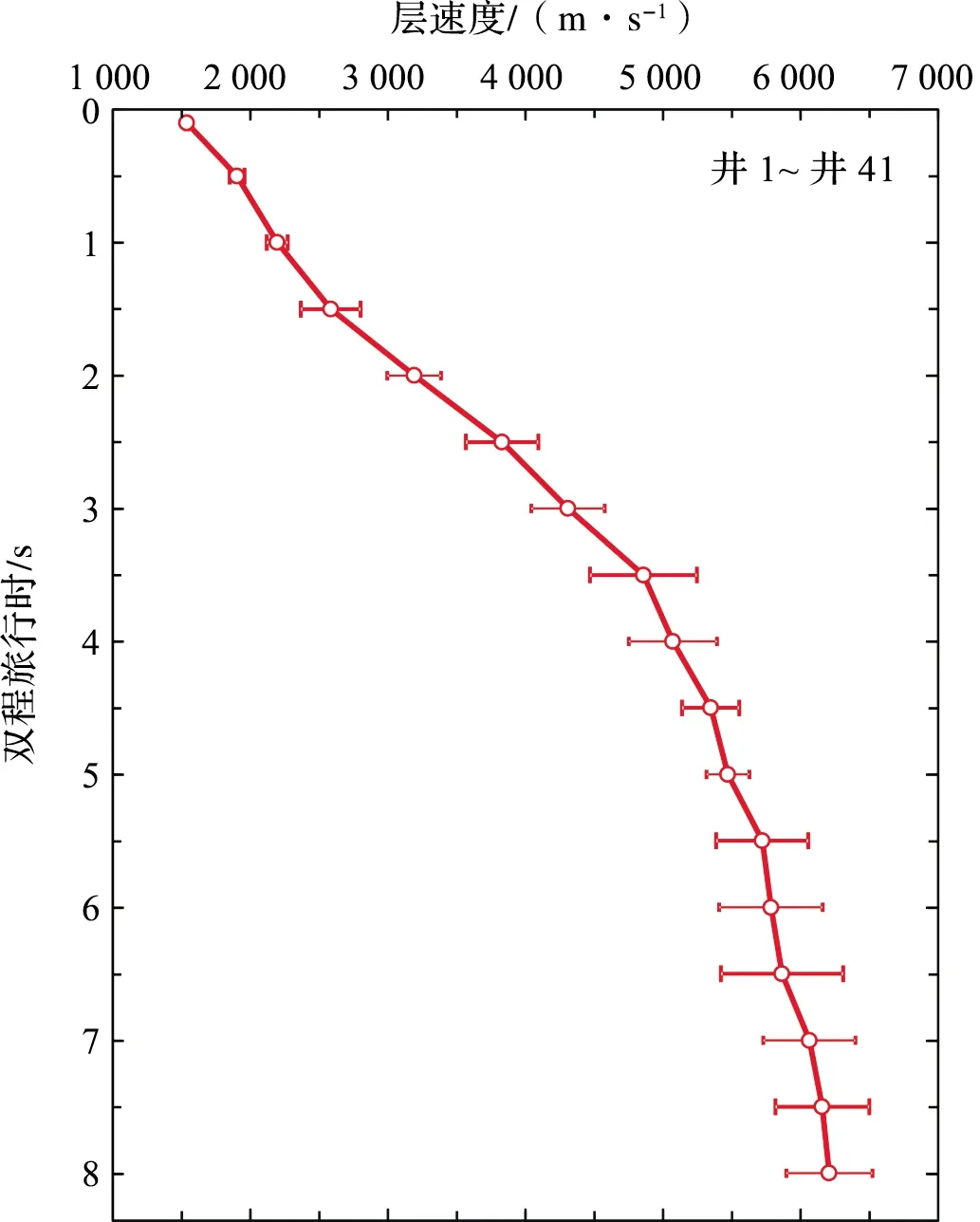
图3 41口钻井速度体平均时速数据Fig.3 Average time-velocity data from velocity volume of 41 drilling holes
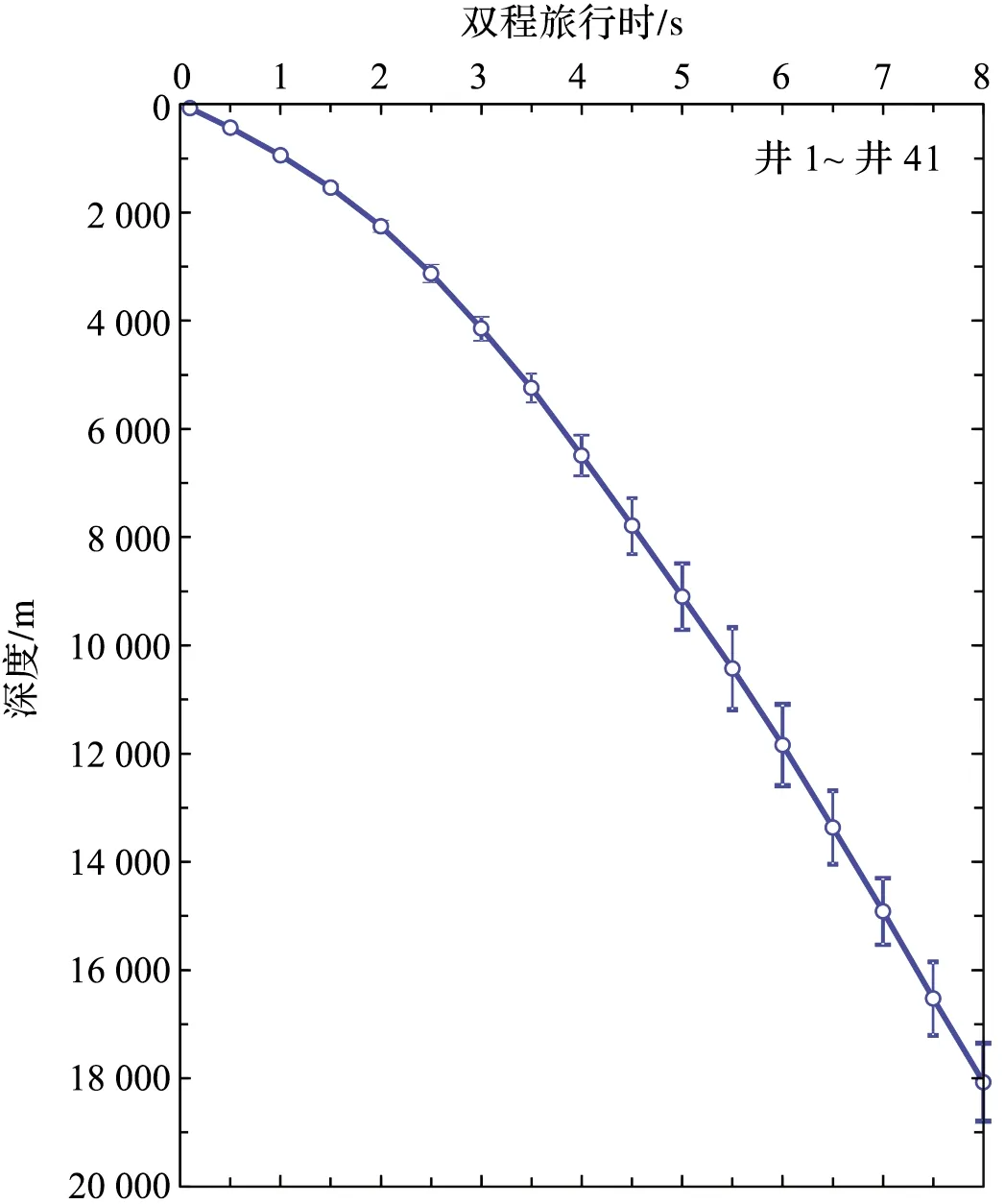
图4 41口钻井速度体平均时深数据Fig.4 Average time-depth data from velocity volume of 41 drilling holes

图5 地震剖面AA′Fig.5 Seismic profile AA′
2 不同模型的拟合效果
本文分别用二次多项式、三次多项式和幂函数来构建时深关系模型,其拟合公式分别为:
Dpoly2=a1t2+b1t
(1)
Dpoly3=a2t3+b2t2+c2t
(2)
Dpower=a3tb3
(3)
式中:D为地层至海底的深度,单位:m;t为双程旅行时,单位:s;poly2和poly3分别表示二次和三次多项式拟合,power表示幂函数拟合;a1、b1为二次多项式的系数;a2、b2、c2为三次多项式的系数;a3、b3为幂函数的系数与指数。
公式(1)、(2)、(3)分别对t求一阶导数再乘以2就能得到与t对应的层速度(简称为拟合速度),公式分别为:
Vpoly2=4a1t+2b1
(4)
Vpoly3=6a2t2+4b2t+2c2
(5)
Vpower=2a3b3tb3-1
(6)
式中:V为层速度,单位:m/s。
对研究区41口钻井的全段VSP数据分别进行时深拟合,得到拟合公式参数(表1)。3种模型在钻井控制深度内都有很好的平均拟合优度,分别为0.999 3、0.999 9和0.993 6。在时深关系的三次多项式模型中,时速关系为二次多项式,根据速度向深部增高,且增速逐渐减小的地质规律,可以推断只有三次项系数为负和二次项系数为正时才可用该模型,否则在将三次多项式拟合时深公式应用于计算深部的层速度时,会发生速度倒转的问题,给出不合理的结果[5]。研究区有38口钻井三次多项式的拟合参数并不满足这一条件,因此在研究区深部地层的时深转换中不建议使用三次多项式模型。
以井-31为例,对二次多项式与幂函数模型在深部地层时深转换中的适应性进行深入分析。井-31 VSP数据的时间域范围是0.56~3.05 s,深度域范围是507~4 170 m(表1),对全段VSP数据进行时深拟合,拟合公式分别为:
Dpoly2=204.1t2+738.9t
(7)
Dpower=974.2t1.255 5
(8)
对应的层速度公式为:
Vpoly2=816.4t+1 477.8
(9)
Vpower=2 446.2t0.255 5
(10)
当TWT在3 s以内,两种模型的拟合曲线与VSP数据的时深点高度重合,拟合效果好,从计算的层速度来看,二次多项式模型在TWT=2 s以内地层拟合效果更佳。在超出钻井控制深度后,两种模型的拟合曲线以不同的变化趋势向下延伸,深度越大,差别也越大。二次多项式拟合深度与实际情况整体较为接近。在3~6.1 s内,拟合深度略小于实际深度,在3~4.8 s之间两者差值逐渐增大至215 m,在4.8~6.1 s之间逐渐减小至0 m,之后拟合深度超过实际深度,且差值随深度增大而增大(图2a)。TWT达到8 s时,井-31处的实际深度是17 871 m,拟合深度是18 968 m,绝对误差为1 097 m,相对误差为6.1%。用时速关系分析造成上述情况的原因(图2b),在3~4.8 s之间,拟合速度小于实际速度,所以拟合深度偏小,该偏小值随时间增加逐步增大。4.8 s 时拟合速度与实际速度都为5 397 m/s。在4.8 s 后,拟合速度大于实际速度,拟合深度逐渐接近实际深度,在6.1 s后超过了实际深度。当TWT=8 s 时,实际速度为6 366 m/s,拟合速度为8 006 m/s,绝对误差为1 640 m/s,相对误差为25.8%。根据速度趋势来看,随着地层深度的增加,拟合深度与实际深度的差值会越来越大。换言之,在TWT=8 s以下的深层,二次多项式拟合结果的误差将越来越大。
幂函数拟合深度在3 s之后与实际情况偏差较大(图2a)。模型的拟合深度在3 s之后小于实际深度,且偏差随着深度的增加而增加,这是因为在TWT=2 s 之下的地层中,拟合速度小于实际速度(图2b),时间累积效应会造成拟合深度的偏差随深度逐渐增大。当TWT=8 s时,拟合深度与拟合速度分别偏低25.8%和34.6%。
计算全区41口钻井在8 s时的拟合深度并进行误差统计(图6),结果显示井-31时速与时深拟合偏差的情况具有普遍性。当TWT=8 s时,41口钻井的实际深度分布为17 113~20 016 m,二次多项式拟合深度分布为17 860~22 195 m,其中38口钻井拟合深度偏大。41口钻井的拟合深度的绝对误差最小为62 m,最大为3 345 m,平均为1 636 m;相对误差最小为0.3%,最大为19.8%,平均为9.2%;与之对应的层速度较实际速度平均偏高36.2%。幂函数拟合深度为7 919~15 917 m,全部偏小,绝对误差最小为1 334.85 m,最大为10 660.6 m,平均为5 275.32 m;相对误差最小为7.7%,最大为57.3%,平均为28.9%;与之对应的层速度较实际速度平均偏低35.6%。综上,幂函数模型的拟合深度与计算的层速度在钻井控制深度以下比实际值显著偏小,拟合效果差,不建议使用。二次多项式模型的拟合深度在TWT为6 s内误差较小,6 s后误差逐渐增大;由其计算的层速度在TWT=4 s后偏差较大,且速度随时间匀速增大,不符合地质规律,在TWT=4 s以下地层不建议使用二次多项式模型。
3 不同层段的VSP数据对深部地层拟合效果的影响
针对二次多项式与幂函数在深部地层(TWT>3 s)的拟合问题,本文尝试对VSP数据采取分段拟合的方法来建立模型,并考察用不同时段的VSP数据建立的模型在深部地层的适用性。研究区钻井VSP数据的时间域范围是0~3.65 s,本文首先以中间值1.8 s为界将每口钻井的VSP数据分为前后两段,分别用二次多项式与幂函数进行拟合。
以下仍以井-31为例进行分析。1.8 s前VSP数据的二次多项式与幂函数拟合公式分别为:
(11)
(12)
对应的层速度公式分别为:
(13)
(14)
1.8 s后VSP数据的拟合公式分别为:
(15)
(16)
对应的层速度公式分别为:
(17)
(18)
式中:上标b表示据1.8 s前的VSP数据,上标a表示据1.8 s后的VSP数据。
只使用1.8 s前VSP数据的两种模型的拟合结果与使用全段VSP数据相比有明显变化(表2)。对于二次多项式模型,二次项系数明显减小,一次项系数略微增大,拟合深度受二次项系数影响明显减小,拟合速度随时间匀速增加,但增速减慢。对于幂函数模型,系数增大不明显,指数减小幅度较大,拟合深度受指数影响显著减小,拟合速度增速也相应减慢。只使用1.8 s后VSP数据的模型拟合结果的变化则相反。对于二次多项式模型,拟合深度增大,拟合速度增速加快;对于幂函数模型,拟合深度明显增大,拟合速度增速也加快。
进一步的计算与对比可以发现,上述分段模型中,基于1.8 s后VSP数据的幂函数模型,对1.8 s以下深部地层的速度与深度拟合结果与实际情况吻合较好(图2)。该模型中,TWT=8 s时拟合深度为16 767 m,比实际深度小1 104 m,相对误差为6.2%;拟合速度为6 055 m/s,比实际速度慢311 m/s,相对误差为4.9%,拟合效果理想。而其它模型都存在明显的缺点,例如使用1.8 s后VSP数据的二次多项式模型在TWT=4 s以下地层中的拟合速度明显偏大;基于1.8 s前VSP数据的二次多项式模型虽然在TWT=1.8 s以上地层中的拟合效果较好,但在TWT=1.8~8 s内的地层中拟合速度偏小,导致拟合深度误差较大(图2)。
全区钻井的分段拟合结果显示,上述井-31拟合结果受控于VSP数据的分段选取的情况在其它钻井中也普遍存在。总体而言,在二次多项式与幂函数模型中,选取的VSP数据层段越深,拟合深度越大,计算的层速度也越大。幂函数模型对VSP数据层段的变化极为敏感,使用不同层段数据的拟合结果差异极大;二次多项式比较稳定,拟合结果差异较小。
从拟合效果来看,选取不同层段的VSP数据进行时深拟合,拟合效果不同,其中基于1.8 s前VSP数据的二次多项式模型在TWT=1.8 s以上地层中的拟合效果较好。只使用1.8 s后VSP数据的幂函数模型最接近实际情况,在该模型中当TWT=8 s时,41口钻井的平均拟合深度为17 252 m,比实际小888 m,相对误差为4.9%,平均拟合速度为6 327.1 m/s,比实际快119.1 m/s,相对误差为1.9%。这可能是因为该模型中拟合速度随地层深度增加而增加,且增速逐渐减小,符合地质规律。
4 VSP数据最佳层段的选取
根据上述以1.8 s为节点分段拟合的结果,本文用幂函数模型对井-31不同层段的VSP数据进行了试验,结果表明使用2.0 s后的VSP数据拟合效果最好(图2)。当TWT=8 s时,井-31的拟合深度为17 230 m,比实际深度小641 m,相对误差为3.6%;拟合速度为6 327 m/s,比实际速度慢39 m/s,相对误差为0.6%,拟合效果极佳。
深入分析井-31的VSP时速数据,发现在0~2 s内,层速度随双程旅行时的增加而增加,增速基本不变,在2.0 s后增速有明显改变(图7),将2.0 s称为井-31的增速拐点,据此识别确定其余40口井的增速拐点,确定研究区41口钻井的增速拐点分布在1.5~2.4 s 之间,平均为1.9 s(图8)。用幂函数分别对41口钻井的增速拐点后的VSP数据进行拟合,结果表明,当TWT=8 s时,41口钻井的平均拟合深度为17 546 m,比平均实际深度小594 m,相对误差为3.3%;平均拟合速度为6 499 m/s,比平均实际速度快291 m/s,相对误差为4.7%(图6),拟合效果进一步提高。
需要注意的是,由于增速拐点的识别与定位具有一定的主观因素,因此,增速拐点可能存在一定的误差。另外,某些钻井增速拐点的位置可能并不明显,这也增大了增速拐点识别的不确定性。
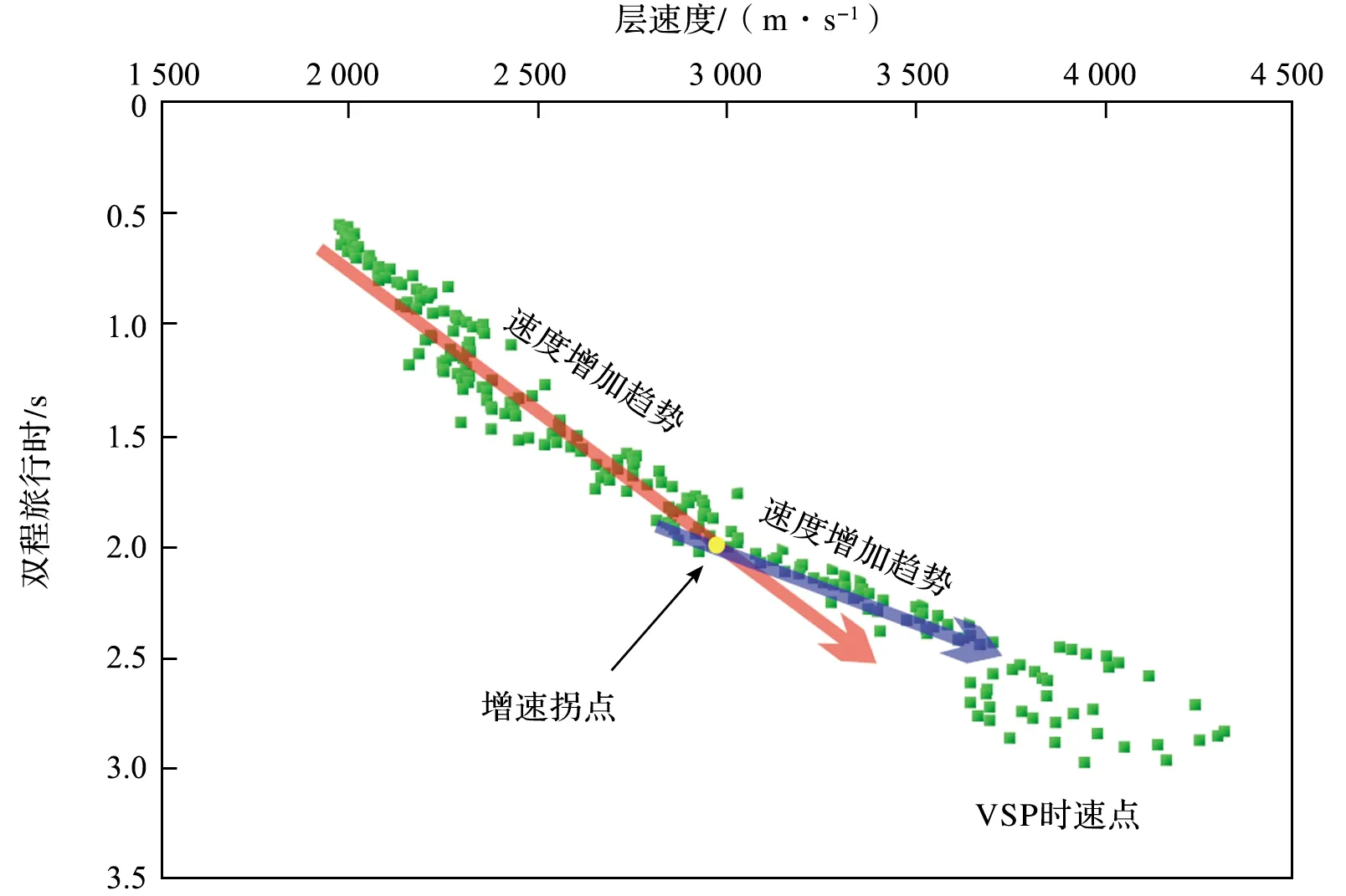
图7 井-31中层速度变化趋势图Fig.7 Variation trend of interval velocity in well-31
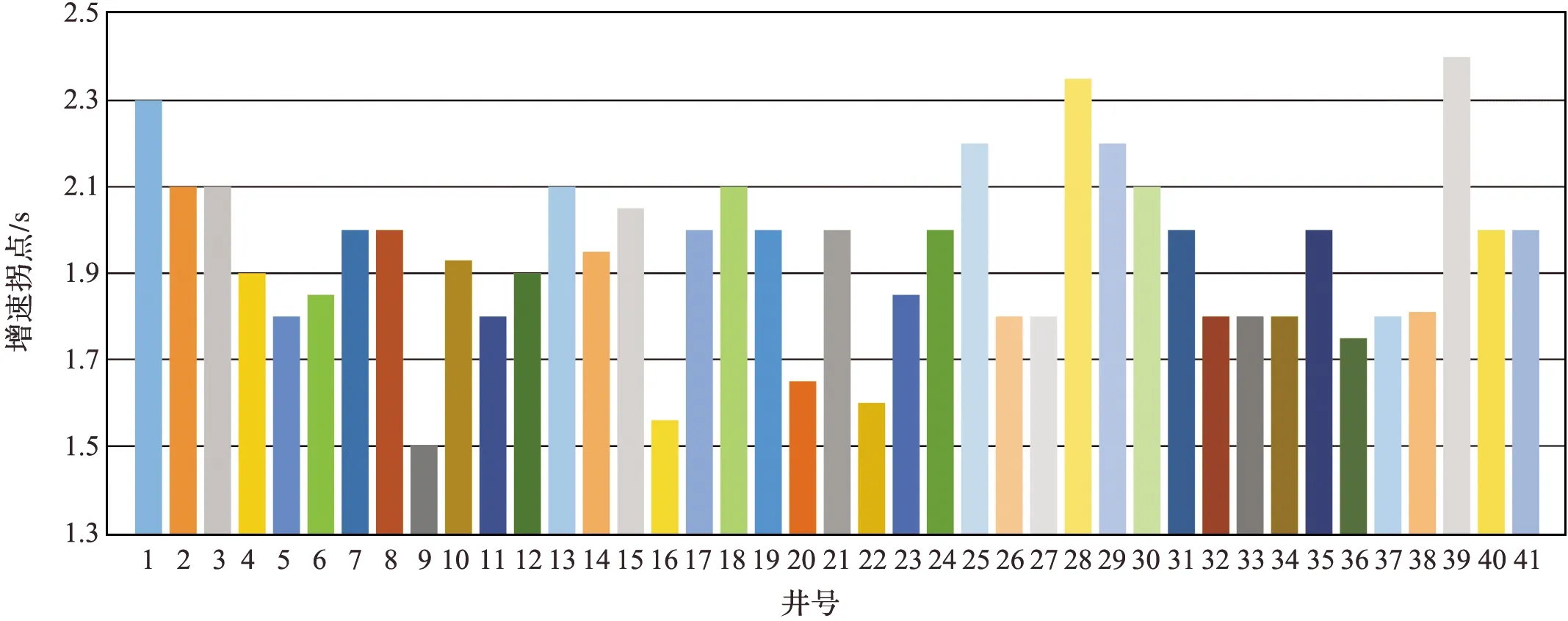
图8 41口钻井的增速拐点Fig.8 Interval velocity increase turning points of 41 drilling holes
5 分段拟合模型的建立
上述研究表明,在研究区用二次多项式对增速拐点以上的VSP数据进行拟合,结果可适用于增速拐点以上地层;用幂函数对增速拐点之后的VSP数据进行拟合,结果可适用于增速拐点以下地层。如前所述,本研究区41口钻井的增速拐点在1.5~2.4 s之间,平均为1.9 s。为了简便,这里近似地取增速拐点为2 s。据此对全区41口钻井的VSP数据进行分段拟合,建立适用于研究区时深转换的分段拟合模型(图9):
D=219.3t2+705.3t(0 ≤t<2 s)
(19)
D=818.3t1.466(2 s ≤t)
(20)
此外,多条地震剖面显示研究区的莫霍面在11 s左右(图5),分段拟合模型在11 s的平均拟合深度为27 516 m(图9),平均拟合速度为7 334 m/s(图10),这与前人研究成果基本一致[10-13],表明改进后的模型在研究区深部圈层也适用。
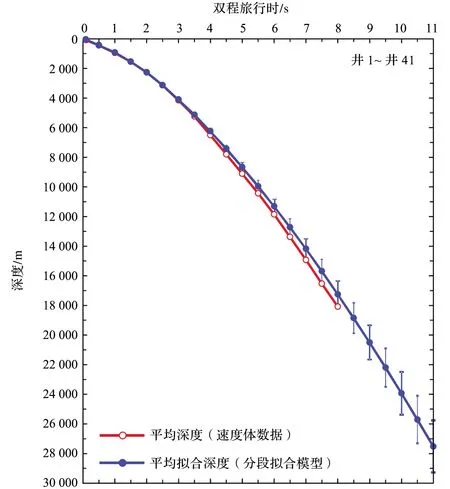
图9 速度体数据与分段拟合模型时深数据对比图Fig.9 Comparison of time-depth data from velocity volume data and segmented fitting model
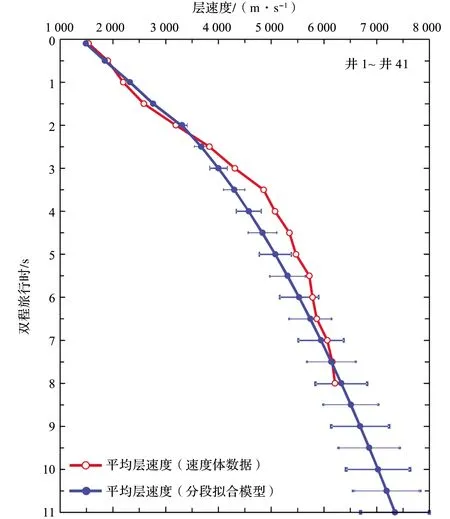
图10 速度体数据与分段拟合模型时速数据对比图Fig.10 Comparison of time-velocity data from velocity volume data and segmented fitting model
6 结论
本文利用多项式和幂函数对东海陆架盆地中部某凹陷41口钻井VSP数据进行了时深拟合,并通过与地震速度体数据以及多道地震剖面反射特征的对比,对拟合公式在深部地层的适用性进行分析,建立了适用于研究区时深转换的分段拟合模型,得到以下主要认识:
(1)基于全段VSP数据的二次多项式与幂函数的时深拟合结果,在钻井VSP数据段内(TWT≈0~3 s)这两种方法的平均拟合优度都超过0.99,时深拟合效果优良。在VSP数据段外,幂函数模型的拟合深度与层速度比实际值明显偏小,不建议采用;二次多项式模型的拟合深度在TWT=6 s内误差较小,但由其计算的层速度在TWT=4 s后与实际速度偏差增大,因此在TWT=4 s以下地层不建议使用。
(2)使用不同层段的VSP数据进行时深拟合的结果不同,一般来说,层段越深,拟合深度就越大,计算的层速度也越大;幂函数模型对层段深度的变化极为敏感,拟合结果差异较大。
(3)钻井VSP数据存在增速拐点,使用幂函数模型对增速拐点之后的VSP数据进行拟合的效果良好,拟合深度与计算的层速度可适用于莫霍面以上岩层。不同井的增速拐点不同,研究区的增速拐点分布在1.5~2.4 s之间,平均为1.9 s。
(4)取研究区VSP速度增速拐点的近似值为TWT=2 s,在2 s之上和之下地层分别利用二次多项式与幂函数进行拟合,建立适用于研究区时深转换的分段拟合模型为:D=219.3t2+705.3t(0≤t<2 s);D=818.3t1.466(2 s≤t)。
致谢本研究钻井VSP数据与地震数据均由中海油上海分公司提供。同时感谢两位审稿专家对本文提出的宝贵意见。

