农村地籍测量中抵偿高程面独立坐标系建立和转换
胡著翱 邓军红 彭飞

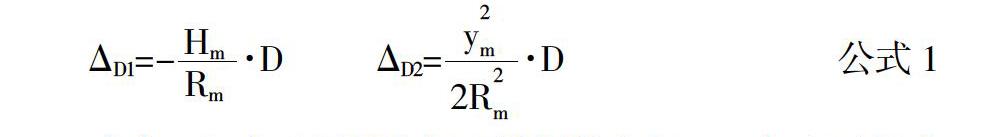
摘 要:在农村地籍测量中,以村庄为单位建立抵偿高程面独立坐标系统可以满足规范要求的坐标系长度变形要求。在实际应用中,用“坐标缩放法”正、反算公式直接进行坐标改正,方法简单,逻辑严密,并通过算例和实例验证,可广泛引用于各种抵偿高程面独立坐标系之间的转换。
关键词:地籍测量;抵偿高程面;坐标缩放法;坐标转换
中图分类号:P226.3 文献标志码:A 文章编号:2095-2945(2020)10-0079-03
Abstract: In rural cadastral survey, the establishment of an independent coordinate system of compensating elevation plane based on the village can meet the requirements of the specification for the length deformation of the coordinate system. In practical application, the forward and inverse calculation formulas of "coordinate scaling method" are used to correct coordinates directly. The method is simple and logical, and verified by numerical examples and examples, thereby can be widely used in the conversion between independent coordinate systems of various compensating elevation planes.
Keywords: cadastral survey; offset elevation surface; coordinate scaling method; coordinate transformation
引言
根据《地籍调查规程》(TD/T 1001-2012),在地籍测量中,当长度变形值大于2.5cm/km时,坐标系统应根据以下具体情况依次选择:(1)有抵偿高程面的高斯投影统一3°带;抵偿高程面为调查区域平均高程面;(2)高斯投影任意带的平面直角坐标系统;(3)有抵偿高程面的任意带的平面直角坐标系统;抵偿高程面为调查区域平均高程面。
在进行农村地籍测量时,对于面积和高程落差较大的地区,无法构建以县区为单位的统一坐标系。为了满足规程要求,可以以村庄为单位建立抵偿高程面独立坐标系,以村庄平均高程作为抵偿高程面,以村庄中心点坐标为中心,采用“坐标缩放法”进行坐标改正,既保证村庄位置不变,又可控制坐标系长度变形。
1 抵偿高程面独立坐标系建立和转换流程
在进行农村地籍测量时,高等级控制点密度和精度满足每个村庄加密图根控制点测量的需要。高等级控制点坐标一般为国家统一3°带1980西安坐标系坐标。在面积较大或高程落差较大的县区,为了满足当长度变形值不大于2.5cm/km的要求,坐标系统可选择以村庄为单位建立抵偿高程面独立坐标系,在高等级控制点满足要求的前提下,独立坐标系建立和转换流程如下:
(1)在高等级控制点的基础上,进行加密控制测量,测出每个村庄的图根控制点坐标。该坐标为国家统一3°带1980西安坐标系高斯平面坐标。
(2)根据各图根控制分布情况,找出接近村庄中心位置的图根点,作为村庄独立坐标系的中心点坐标,保持该中心点坐标不变。
(3)根据各图根控制点高程,计算出村庄的平均高程,作为抵偿高程面高程。根据抵偿高程面归化计算公式(见公式1),计算出椭球面缩放系数(见公式2)。
(4)按照“坐标缩放法”抵偿高程面换算公式(见公式3),对每个图根点到村庄中心点之间的距离进行改算,得出每个图根点在村庄抵偿高程面独立坐标系中的高斯平面坐标。
(5)利用村庄内部的图根控制点独立坐标系坐标,进
行村庄地籍碎部测量。
(6)为了满足整个县区所有村庄地籍测量成果统一管理和汇交需要,根据“坐标缩放法”原理和坐标反算公式(见公式6),借助GIS软件,将各村庄地籍图矢量数据反算到统一坐标系中。
2 抵偿高程面归化公式
众所周知,实地测量的边长D投影到高斯平面坐标系中有两次变形的影响[1],即测距边长归算到参考椭球上的变形?驻D1和将参考椭球上的边长归算到高斯投影面上的变形?驻D2。
式中:Hm表示测距边长两端平均高程,Rm表示测距边长中心点处平均曲率半径,ym表示测距中心点到中央经线距离。
上式中,测距边长归算到参考椭球上的变形?驻D1的计算公式即为抵偿高程面归化公式,抵偿高程面引起的长度变形与抵偿面高程成正比,与测距边长中心点处平均曲率半径成反比。假设测距边长抵偿高程面变形缩放系数为m,则:
式中的正负号跟Hm有关,如果由参考椭球面向抵偿高程面转换,则为正,反之为负。如果由一个抵偿高程面向另外一个抵偿高程面转换,公式1、公式2仍然成立,Hm即为目标抵偿高程面高程-原抵偿高程面高程,公式2中的正负号与Hm的正负号一致。
3 “坐标缩放法”换算公式
从严格意义上说,抵偿高程面改正的坐标计算可以采用膨胀椭球法,通过改变椭球参数,利用高斯投影公式重新计算坐标,但过程比较繁琐[2]。在高斯平面坐标系中,采用坐标直接改正的方式进行换算,方法简单、易于操作[2,3],本文在中心点坐标的選取方法上稍有区别,称之为“坐标缩放法”坐标换算。张宏在《宅基地使用权和建设用地使用权调查控制测量的一种方法》[3]中详细论证了该方法和公式的正确性和严密性。
假设某点换算坐标为(X,Y),换算后坐标为(XH,YH),本村中心点坐标为(X0,Y0),现用抵偿高程面高程为H0,转换后抵偿高程面高程为H1,地球平均半径Rm,“坐标缩放法”坐标换算公式如下:
式中,目标抵偿高程面H1和现用抵偿高程面H0,如果为参考椭球体高程面时,高程为0。该公式,可实现两个不同抵偿高程面之间的直接换算,也可以实现参考椭球面向任意抵偿高程面坐标系之间的正反算。
算例:
已知某村图根控制点P1国家统一3°带1980西安坐标系坐标为(X,Y)=(4007037.124,479157.423),本村中心點国家统一3°带1980西安坐标系坐标为(X0,Y0)=(4006586.403,479503.814),现用抵偿高程面高程H0=350m,换算后目标抵偿高程面高程为H1=400m,Rm=6378140m,换算后该点坐标为(XH,YH)。代入公式3可求得(XH,YH)=(4007288.397,479156.135)。
同时已知图根点在国家统一3°带1980西安坐标系高斯平面直角坐标为(X,Y)=(4007037.100,479157.442),则H0=0m,目标抵偿高程面高程H1=400m,根据公式3求得变换后控制点坐标为(XH,YH)=(4007288.398,479156.135)。
两者相差(?驻X,?驻Y)=(0.001,0.000),坐标基本一致。
4 基于GIS软件进行矢量图形坐标系转换
以河南省某县级市农村集体土地使用权地籍测量为例,该市地籍图共牵扯到500多个行政村,数据量巨大,几乎每个村庄各建立了一个抵偿高程面独立坐标系,根据《河南省地籍调查县级平面直角坐标系建设若干意见》的有关要求,为确保各项数据库建设项目成果坐标系统统一,奠定地籍管理规范化建设的技术基础,“平面坐标系统以县(市)为单位统一建立”。因此,需要将以村庄为单位建立的抵偿高程面独立坐标系成果,换算到统一的坐标系中。成果换算以地籍图为主,需要考虑矢量图形转换方法,借助GIS软件进行矢量图形坐标系变换。
从公式3可以看出,由于换算前后的坐标计算是一个线性公式,可以分为两个部分,一个平移量,另外一个是椭球缩放量。
假设平移量表示为(?驻X,?驻Y)则:
假设缩放量表示为(KX,KY),则:
则“坐标缩放法”坐标反算公式如下:
本实例采用苍穹地理信息系统软件(KQGIS)进行坐标系换算,苍穹软件可将各村的地籍图直接进行系统变换,根据公式6和苍穹软件的功能设置,分平移和缩放两步进行变换。
第一步计算平移参数,由公式4计算可得(?驻X、?驻Y)。然后利用苍穹软件的带参坐标转换功能进行转换即可。
第二步进行椭球缩放。利用投影系统转换功能,将转换前的椭球面的长半轴加上现用抵偿高程面高程H0,并保持偏心率不变,计算出短半轴数值。转换后的椭球面长半轴加上目标抵偿高程面高程H1,并保持偏心率不变,计算出短半轴数值,转换即可。
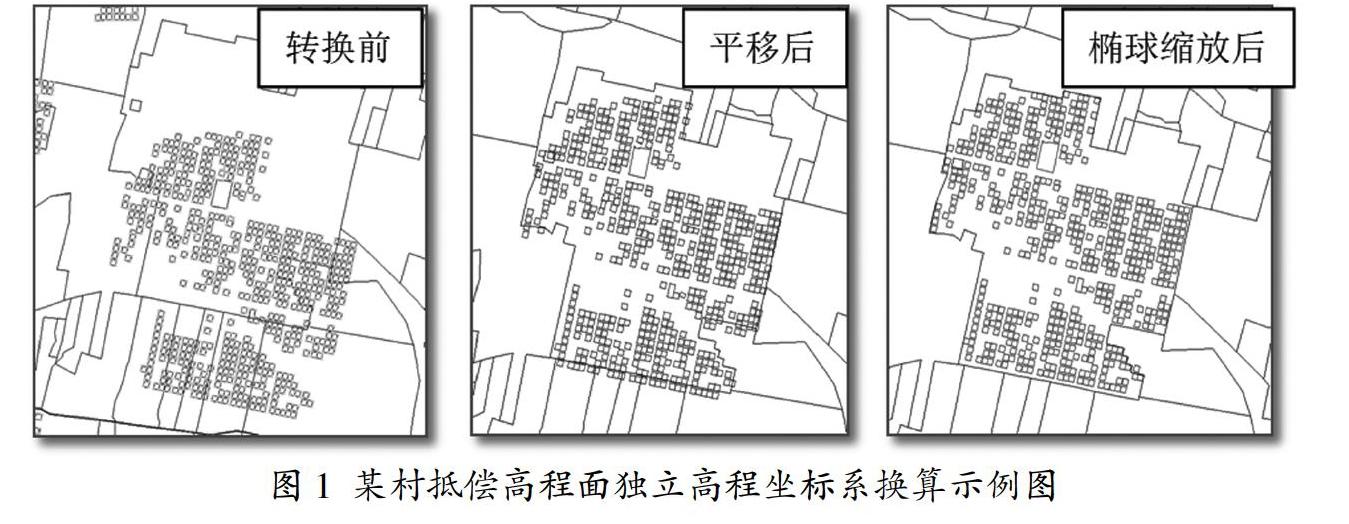
从图1可以看出,经过苍穹软件处理,转换前宗地图层与目标图层差距较大,经过平移后宗地图层与目标图层已经比较接近,再通过椭球缩放变换后宗地图层和目标图层完全套合。
在实际操作中,为了保证转换精度和成果质量,每个村庄至少取1个控制点进行转换前后的坐标对比验证。在实验村庄中,对控制点图层转换后,以图上解析坐标的方式,得到控制点P1的坐标为(4007288.397,38479156.135),与上节算例通过公式计算的坐标(4007288.397,479156.135)完全吻合,说明利用GIS软件进行矢量图形转换结果,和公式计算法计算结果完全一致。
5 结论
在农村地籍测量中,以村庄为单位建立抵偿高程面独立坐标系统可以满足规范要求的坐标系长度变形精度,在范围面积大或高程落差大的县区广泛采用此种方式。在实际应用中,用“坐标缩放法”计算公式直接进行坐标改正,方法简单,逻辑严密,适用于抵偿高程面独立坐标系的建立和转换,可广泛应用于农村地籍测量中。
为了满足农村地籍成果统一管理和汇交的需要,需要将各个村庄的独立坐标系地籍矢量图形,转换到全县区统一的坐标系中,可借助于GIS软件,用“坐标缩放法”反算公式,分平移和缩放两步进行图形坐标系统转换。通过算例和实例验证,该方法计算正确,满足规范要求,解决了实际生产问题。
参考文献:
[1]孔祥元,梅是义.控制测量学[M].武汉:武汉测绘科技大学出版社,2000,2:23-26.
[2]宋臣,张立宝.村庄地籍调查中抵偿高程面的选择方法[J].测绘与空间地理信息,2017(9):213-215.
[3]张宏.宅基地使用权和集体建设用地使用权调查控制测量的一种方法[J].测绘与空间地理信息,2015(2):198-201.

