立体几何体积的三种常规解题方法分析

杨 徽

(重庆市酉阳第一中学校 重庆酉阳 409800)

引言

笔者从历年的高考数学卷题目分布研究中发现，立体几何在整张数学卷子中所占比例很大。立体几何的题目一般会在选择、填空题的最后几题和大题的第二、三题的位置中分布，主要考查学生对立体几何基本知识点的了解程度，以及对立体几何与向量、平面几何等知识点相结合的理解能力。[1]

一、适当分割，多个求和

一般的数学考题中，关于体积的计算，不会是一个简简单单的长方体、正方体或是三棱锥，而是几个长方体、正方体的结合形成的多面体，求它们相结合形成的体积。[2]在此类型中，最常见的解题方法就是分割法，把多面体分割成几个我们常见的立体几何。然后，分别求出每个分割体的体积。最后，将所有的分割体体积相加，就能得出总体积了。例如，在多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF//AB，EF=1.5，EF与平面AC的距离为2。那么，该多面体的体积是多少？在本题中，由于多面体ABCDEF是一个不规则的立体几何图形，我们无法用常见的立体几何的体积算法，去计算该多面体ABCDEF的体积。此时，我们便可以运用分割法的知识，将多面体ABCDEF分割成常见的立体几何，再进行计算。我们先连接BE、CE构成一个新的平面BCE，这个平面将多面体ABCDEF分割成了四棱锥E-ABCD和三棱锥E-BCF。此时，多面体ABCDEF的体积就等于四棱锥E-ABCD的体积加上三棱锥E-BCF的体积。教师可以引导学生得出V多面体ABCDEF=VE-ABCD+VE-BCF，在进行求解。

二、先补后减，整体计算

第二种关于立体几何体积的常见算法，是与分割法相对的补形法。我们把题中所给的多面体用常见的立体几何加以拼凑，把它拼成常见的立体几何。然后，在求出这个大的立体几何的体积后，再把补上去的，小的立体几何的体积算出来，两者相减就能得出多面体的总体积了。例如，已知斜三棱柱的侧面A1ACC1与平面ABC垂直，∠ABC是直角，BC=2，AC=，且AA1⊥A1C，AA1=A1C，求点C到侧面A1ABB1的距离。

对于斜三棱柱ABC-A1B1C1。因为，是斜三棱柱的缘故。所以，在计算点C到平面A1ABB1D距离时，两者是线面关系，线面关系会很难计算。此时，我们便可以运用第二种计算立体几何的体积算法—补形法。将斜三棱柱ABC-A1B1C1补成一个平行六面体ABCM-A1B1C1M1。然后，我们再设点C到平面A1ABB1D的距离为d，而在平行六面体ABCM-A1B1C1M1中，d也是平面A1ABB1与平面C1CMM1之间的距离，作A1D⊥AC于点D，作A1E⊥AB于点F。因为，AA1=A1C，AC=，AA1⊥A1C。所以，A1D=。又因为∠ABC是直角，BC=2。所以，AB=。因为，侧面AA1CC1与底面ABC垂直，A1D⊥AC于点D。所以，A1D⊥AB，又A1E⊥AB于点F，已知AB⊥面A1ED。因而，AB⊥ED，又∠ABC是直角。所以，DE∥BC，D为AC中点，且，

三、等底等高，相互转化

“等底等高，相互转化”，即是我们常说的等面积法。把原本不容易得出的底面面积或高，通过代替的方式转化为比较容易得出的底面面积或高。当我们在求四面体P-ABC的体积时，由于顶点P到底面ABC的距离h1不容易得出，我们可以换一个点作为顶点，将四面体P-ABC换成四面体A-PBC。此时，我们会发现，顶点A到面PBC的距离h2就可以很容易得出，从而我们可以计算出四面体A-PBC的体积，而这种简单的转化法就是我们常说的等体积法。例如，在棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD=2，PD⊥底面ABCD，若PD=AD=l，请求出棱锥D-PBC的高。

∵底面ABCD是平行四边形，且AB=2AD=2

∴AB=CD=2，AD=BC=1

又∵∠DAB=60°

∴由余弦定理可以算出BD=

∴BC⊥BD

又∵PD⊥底面ABCD

∴BC⊥PD

∴BC⊥平面PBD，BC⊥PB

在Rt▲PDB中

∵PB=2，V棱锥D-PBC=V棱锥D-PBC

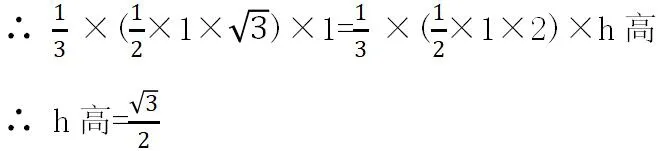
即菱锥D-PBC的高为。

四、总结

总之，想要学好立体几何，教师就要让学生把立体几何当中的知识点理清楚。然后，在一般的基础上理解体积计算的各种方法，明白每一种方法之间的变通，让学生在实践过程中能运用这些巧妙的方法，更好地掌握该知识点。