对规律性瞬时尖峰数据的一种降维优化处理方法

卜鸿翔

（南瑞集团有限公司 江苏省南京市 211106）

1 引言

在电力行业中，通常对用电负荷以每15 分钟采样一次的频率记录用户的日用电详细情况，每日共采样96 个负荷特征值。在大数据分析中，这96 个负荷特征值（即96 个变量）组成的高维分析源数据，存在信息相似、采集异常、数据跳变等特点，一般需要进行数据预处理和降维处理，以便于进一步使用。在以往研究中，为了分析方便，普遍会将所有异常信息识别为脏数据后进行剔除，而在实际应用中，特别是对单个用电企业日用电情况分析中，由于一些外部影响因素持续发生影响，其日负荷数据的瞬时性尖峰值数据在相邻一段时间内会规律性重复出现，所以该类数据不应该被当成脏数据被去除，而基于保留的这些规律性瞬时尖峰数据，在进一步用PCA 方法做降维处理后，日负荷曲线会出现尖峰特征失真的情况，对后期分析产生较大影响。为了解决这一问题，本文提出一种方法，改变PCA 基于数据之间的距离进行因子加权的做法，采用信息熵加权方法（基于数据密度进行因子加权）进行特征提取处理，以保留分析原数据原有的特征。

2 规律性瞬时尖峰数据的处理困境

本文所说的规律性瞬时尖峰数据是指在一段时间内，有规律地重复出现的瞬时性峰值波动数据，这类数据发生所用时间不长，但尖峰时段出现有一定的规律，其产生的原因多种多样，既可能是与季节有关的冬季取暖、夏季空调，甚至可能是高铁经过、节假日等造成的。对用电用户的短期用电分析来说，造成尖峰数据的成因在持续发挥作用，不能被简单忽略，需要保留这些数据做全面分析。

图1 为是某省级电网 2016年8月某用户的负荷数据，采样频率为15 分钟，每日共96 负荷值，该用电用户在19:15 左右出现的“钉状”负荷波动，由于在相邻的一段时间均发生，所以不能用常见消除“钉状”毛刺的方法简单剔除，因为这样会导致相关影响因素的丢失。但基于保留的规律性瞬时尖峰数据进行PCA 降维处理后，随着维度的压缩（本文压缩时间段维度，将每日95 个时间段经过PCA 降温后压缩为23:00～8:00、8:00～9:00、9:00～12:00、12:00～17:00、17:00～22:00、22:00～23:00 共6 个时间段），其降维后的日负荷特征曲线如图2 所示。

对比图2 和图1 可知，图2 与图1 负荷特征曲线明显不同，在图2 中19:15 的负荷特征与8:30 左右的负荷特征相比，其“钉状”特征并没有图1 明显，存在特征权限失真情况。

进一步分析可知，基于距离的PCA 降维方法对这类数据并不适用，主要原因在于PCA 基于方差等进行加权处理，是对瞬时尖峰数据的平均化处理，从而导致了尖峰特征的失真，本文将采用一种基于密度的加权处理方法--信息熵加权方法，避免了平均化处理，以最大化保留了尖峰数据的原有特征。

3 信息熵加权方法介绍

信息熵是在1948年由克劳德•艾尔伍德•香农提出，用来一种度量信息量多少的方法，其信息量多是基于各信息源提供信息的概率进行计算，通常高信息度的信息熵则低，低信息度的信息熵则高。

使用信息熵加权方法的思想是：基于不同维度的特征在识别过程中所起的作用不同这一事实，将信息熵作为权值来突出识别重要的特征或样本，从而提高模式识别率。

基于信息熵加权进行特征提取的计算方法如下：

设数据矩阵D 有n 维属性集，m 个数据对象，其也可表示为由t 个子矩阵X 组成。

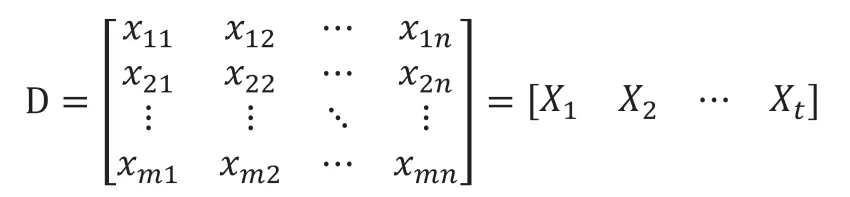
子矩阵X 表现如下：

信息熵加权特征提取的目标是获得保留原始矩阵重要特征的新数据矩阵D'。

步骤1：计算子矩阵Xt中第j 维属性对应的第i 个数据对象的特征值比重：

其中：Mij为特征值比重,xij为特征值,i=1,2,…,m；j=a,a+1,…,b；且

步骤2：计算子矩阵Xt的熵值：

其中：当Mij=0 时，则MijlnMij=0。如果子矩阵中每个对象的特征值完全相等，那么此时Нit=Нimax=1，此时权重最大；当数据对象的特征值相差越大时，也就是在子时间序列里信号波动越大，则Нit越小。

步骤3：对原子矩阵的均值加权，以赋予子矩阵的新特征值。

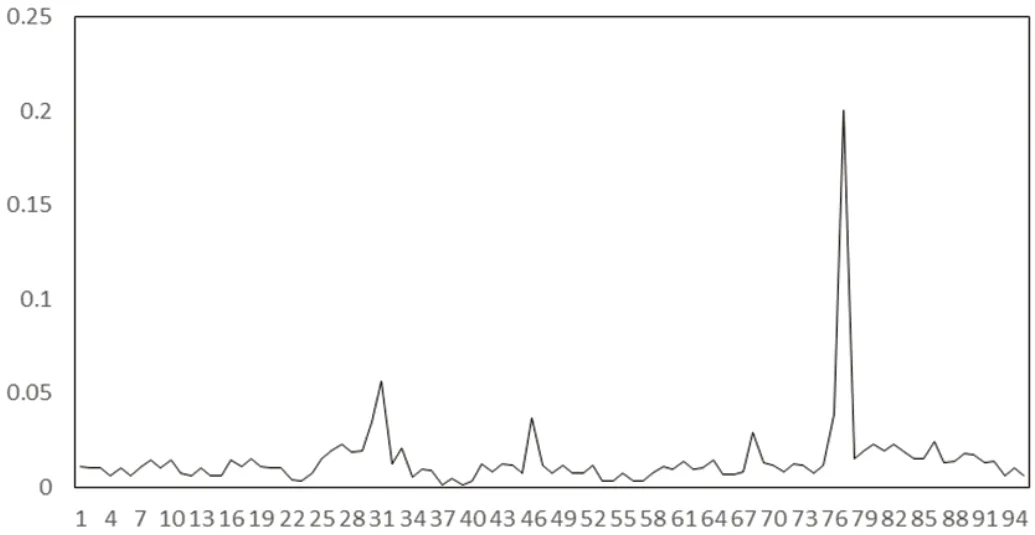
图1：含规律性瞬时尖峰的曲线

图2：基于PCA 降维后的曲线

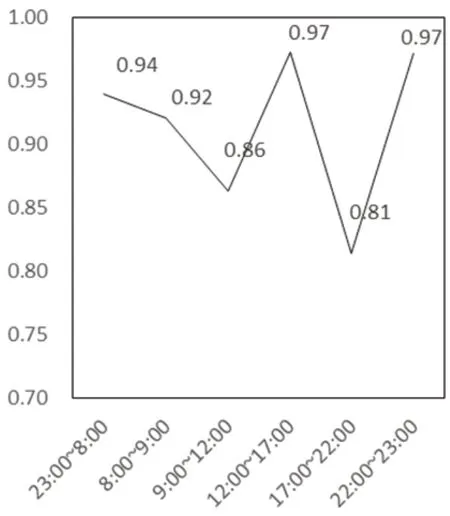
图3：各时段信息熵加权系数

此时ψit是对象i 在子序列t 中的各属性平均值。

4 案例介绍

本案例以图1 的采集数据为样本，基于信息熵加权方法进行降维处理，降维仍然按照图2 的6 个时段进行维度的压缩。

4.1 计算每个时段属性对应的信息熵（加权因子）

根据信息熵加权方法，计算每个时间段的特征值比重（对照计算公式的步骤1），并进一步得到其信息熵（对照计算公式的步骤2），通过计算，6 个时间段对应的值分别为0.94、0.92、0.86、0.97、0.81、0.97（如图3），这说明该用户在9：00-12：00 和17：00-22：00的信息熵较小，即对应时段的负荷波动比其他时段大，尤其是在17：00-22：00 该时段可能会发生一些瞬时功率大幅度变化的事件，这与图1 中19：15 左右出现的“钉状”波动特征类似。

表1：两种方法降维后的聚类结果对比

图4：基于信息熵加权的特征曲线

图5：两种方法降维后的聚类轮廓系统图

4.2 计算每个时段的特征值

基于得到的以上的信息熵作为加权因子，计算作为每个时间段的特征值（对照计算公式的步骤3）,各时段特征值分别为0.06，0.06，0.04，0.04，0.11，0.06，相对应的降维特征曲线如图4 所示。比较图4 与图2 可知，图4 更接近图1 的曲线特征。

4.3 后续应用效果验证

本文在进行降维处理后数据，主要为聚类分析（主要算法为K-means）服务。本验证将选取具有规律性瞬时尖峰特征的用电用户分别基于PCA 和信息熵加权降维处理后进行聚类分析，以验证效果。

为了验证效果的客观性和广泛性，选取某省实际用电用户的日负荷数据作为样本，在用电行为特征上，“朝九晚五型”、“价格敏感型”、“夜间用电型”、“用电稳定型”等用电用户各选取100 个，共400 个样本用户。

评判应用效果的标准主要来自两个方面，一是通过轮廓系数进行评价，它结合内聚度和分离度两种因素，可以在相同原始数据的基础上用来评价不同数据处理方法对聚类结果所产生的影响。二是业务准确度评价，本验证首先根据专家经验，对400 个实例进行主观分类，然后将聚类结果与专家分类相符的个数占总实例个数之比评估业务符合度。

经过计算，使用基于PCA 和信息熵加权降维处理的聚类轮廓系数如图5 所示，PCA 处理后的平均聚类轮廓系数为0.21，信息熵加权处理后的平均聚类轮廓系数为0.27。在技术指标上，后一种进行K—means 聚类效果更好。

两种方法处理后进行聚类后的业务精准度对比如表1 所示，由表可知，后一种方法具有更高的准确率。

5 结论

综上所述，通过本方法的优化，不仅保留了源数据的原始特征，又很好处理了规律性瞬时尖峰数据降维带来的特征失真问题，对处理单个用电企业的用电数据分析提供了一种新的参考方法，本方法不仅适用于电力领域，也适用于其他领域的类似特殊数据的处理。