基于神经滑模变自抗扰控制的感应电机变频调速系统设计

苗立伟

摘   要：基于强化感应电机变频调速系统的调速质量及响应速度的考量，文章设计出建立在神经滑模变自抗扰控制的感应电机变频调速系统。应用ADRC控制，在基础上提升了调速系统控制品质与控制精准性能。综合神经逆控制思想，创建起神经滑模变自抗扰控制器，减少系统的抖振现象，实现对感应电机调速系统转速、转矩、磁链等参数的最优化控制。

关键词：神经滑模变自抗扰控制;感应电机变频调速系统;系统设计

感应电机具有结构简单、成本较低、运行精准度较高等特征，在变频调速系统中发挥着重要的作用。但性能较高的感应电机调速系统的发展，在一定程度上限制于电机时变非线性特征。现阶段具有代表性的感应电机变频调速控制理论主要为转速开环恒压频比（Voltage/Frequency，V/F）控制、转差频率控制、矢量控制（Filed Oriented Control，FOC）与直接转矩控制（Direct Torque Control，DTC）。本研究建立在已有研究成果基础之上，提出基于神经滑模自抗扰控制的感应电机变频调速系统。

1    感應电机现代控制技术简述

1.1  标量控制

交流电机的标量控制属于基于非线性方程在稳态平衡点上的线性化。从这一点来看，凭借电机的稳态数学模型，单纯调节变量的大小，为此，控制效果均符合稳态要求[1]。此种控制方法的优势为能够应用经典的线性控制理论进行控制器的设计。此种设计有助于调整非线性系统动态性能，转变程度如何主要受到距离系统期望平衡点远近的影响[2]。但是，基于交流电机多变量系统，应用标量控制还存在一定的不足，具体表现为系统输入与输出之间的解耦难度较大。

1.2  适量控制

为避免经典标量控制所存在的不足之处，有关学者提出矢量控制理论。此种手段能够经由转矩渐进解耦与对磁链的控制，促使交流电机性能与直流电机一样，在设计控制器环节中还应用到电机非线性数学模型。矢量控制手段的应用建立在解耦与交换坐标基础之上[3]。矢量控制理论经由对电机磁链的控制，将定子电流细分为转矩与磁链，经由非线性反馈电压控制规律直接或是间接完成控制。但存在的一点问题是，基于转子磁链矢量精准度较难实现，且坐标交换的复杂程度较高，很难获取到良好的控制效果。除此之外，定子电流的解耦需要建立在明确的磁链空间位置之上，为此，在矢量控制系统中需要配备测量转子位置或是速度的传感器，导致整个系统装置过于复杂且笨重。

1.3  直接转矩控制

直接转矩控制属于全新的控制手段。与矢量控制不同的是，应用逆变器输出的空间电压矢量直接控制定子磁链矢量与电磁转矩。在实践中不需要转速信息，可在坐标下经由交流电机的数学模型，控制转矩与磁链，极大地简化了中间流程。直接转矩空时也是电压类型控制，具体为经由空间电压矢量对目标定子的磁链与电磁转矩进行调控，基于节省电流环，将空间电压矢量直接设置在电子电感中，不涉及过渡过程，为此速度得到了显著提升。但存在的一点问题是，缺少电流的直接控制会造成电流脉动的增加，进而影响到启动电流。

2    感应电机变频调速系统的数学建模

感应电机属于非线性时变控制对象，在实践期间，电机电阻、电感、气隙磁通过时可受到环境影响。基于分析便捷性的考量，常规会忽视谐波影响，提出立项的假设。依据已有研究结论以及数学逻辑推导，获得感应电机矢量控制下的数学模型公式如下：

在计算简化期间，针对感应电机变频调速系统数学模型应用Clarke交换与Park交换，经由转变，系统数学模型实现简化，在一定程度上减少变量之间的耦合程度与状态变量数量。

3    神经滑模变自抗扰控制器设计

3.1  滑模变自抗扰控制器结构

在控制技术的不断完善下，经典比例、积分和微分（Proportion Integral Differential，PID）无法适应系统精准度与速度的需求，为此，有研究人员提出自抗扰控制技术。自抗扰控制技术控制器的结构主要为跟踪微分器和非线性反馈率以及自抗扰控制器等。在感应电机变频调速系统数学模型中能够发现，转子磁链在完成坐标转变期间，d轴磁链与电流存在耦合，借助于非线性控制理论对数学模型做解耦，不可避免地会形成一定的误差，由此影响到最终控制效果。基于此，应用自抗扰技术能够对此问题加以解决。在自抗扰控制器设计期间，应用3个一阶自抗扰控制器对调速系统转速与电流以及位置进行调控，不同控制器的参数调制均存在差异，完成自身工作。自抗扰控制器可进行宽带响应转速环与电流环的调控，但是控制参数较多。基于减少整定参数的考量，提升调速系统鲁棒性，应用了滑模变结构，构造滑模变自抗扰控制器。

3.2  神经滑模变自抗扰控制器的构造与作用

神经网络逆系统的设置建立在线性化、解耦成为伪线性系统的基础之上。逆系统的实现可分为有解析与无解析两种方式。感应电机属于多输入多输出、强耦合非线性的高阶系统，精准数学模式较难应用破解式进行展现，仅能够应用类似模型来替代。基于神经网络可随意精度逼近复杂静态非线性函数，为此，应用神经网络实现被控系统的逆系统，由此创造出非解析实现形式的逆系统。滑模变自抗扰控制器有助于提升感应电机变频调速系统响应速度及精准度，同时也能够在一定程度上简化参数整定数量，进一步提升系统的鲁棒性。但是，此控制器还需要将被控制对象精准数学模型作为前提基础，但实际上感应电机调速系统自身属于多变量时变系统，构建精准数学模型难度较大。为此，在系统中应用到神经网络逆控制，借助于BP学习法持续靠近调速系统数学模型与滑模变自抗扰控制函数，应用归一化处理数据训练与校验神经网络。

4    仿真与结果

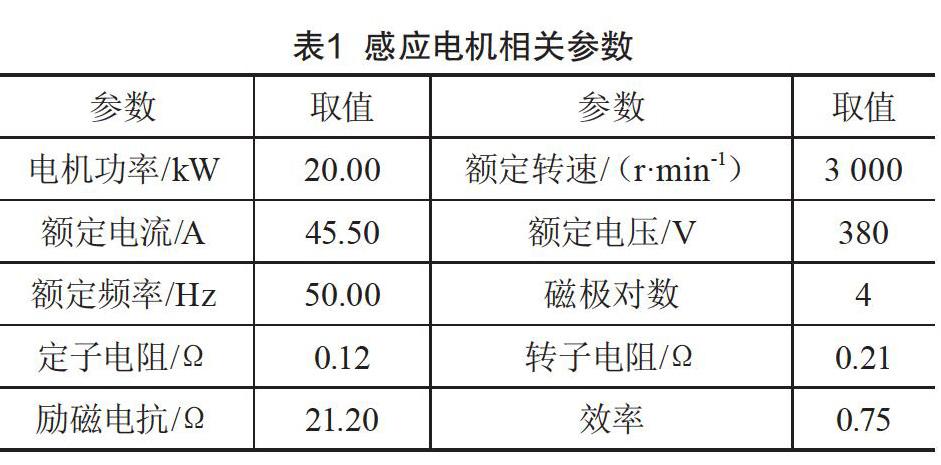
在Matlab中simulink环境下创建感应电机变频调速系统神经滑模变自抗扰控制器仿真模型。感应电机与空间矢量脉宽调制（Space Vector Pulse Width Modulation，SVPWM）模型利用S函数建模，位置控制器与速度调节器应用PID调控;电流调节环应用比例调节和积分调节（Proportional Integral Controller，PIC）。如表1所示，经由持续调控仿真模型的参数，将伸进滑模自抗扰控制调速系统与加入PID算法的变频调速系统做对比。仿真结果显示，加入神经滑模自抗扰控制算法的变频调速系统相对于仅仅加入传统PID控制变频调速系统，在调速质量、平温度、响应速度上均具有更大的优势。在Simulink环境做仿真实验，结果发现，基于神经滑模自抗扰控制感应电机变频调速系统的平温度以及高速响应速度等优势，整个系统的可靠性均有所提升。

5    结语

在电机控制理论、现代控制理论与非线性控制理论的完善下，为感应电机变频调速向高性能方向发展提供理论支持。感应电机自身属于多变量、非线性的时变系统，电磁转矩、速度等实现控制的难度较高，促使电机的调速性能没有办法提升。经本次研究发现，在感应电机变频调速系统中引入神经滑模变自抗扰控制器，可促使整个系统的稳定性、速度、抗干扰强度等均得到提升。

[参考文献]

[1]郭金妹，张建荣，陈磊.基于神经滑模变自抗扰控制的感应电机变频调速系统的研究与设计[J].科技与创新，2019（12）：16-18.

[2]张晖鹏，于海生，刘旭东，等.异步电机四象限驱动系统的线性自抗扰与滑模控制[J].青岛大学学报（工程技术版），2019（2）：1-7.

[3]李益敏，陈愚，李云龙.基于滑模自抗扰的永磁同步电机控制系统设计[J].电气传动，2019（8）：22-25.