《确定位置》教学实录与评析

陈云帆 陆凯

《确定位置》是人教版数学六年级上册“图形与位置”板块的最后一个内容，它侧重对各部分知识的融合，即用已经学习过的方向（角度）、距离来确定位置。本课教学让学生在具体的情境中经历用方向和距离描述物体位置方法的探索过程，体会用方向和距离确定物体位置的科学性，注重培养学生的观察能力、识图能力和表达能力，发展学生的空间观念，通过“图形与位置”知识的前后联系，初步感受坐标几何体系。

一、创设情境，激发兴趣

师：同学们看大屏幕，请问这是什么？（课件演示台风“山竹”）

生：台风。

师：对。这是2019年登陆我国内地的最强台风“山竹”，我们也把它称为“风王”。就在台风“山竹”即将来临当天，我国海域上有一艘船突然发生故障，无法继续航行，被迫停在了海面上。你看到这艘船了吗？（播放茫茫大海的视频）

生：没看见。

师：海面风高浪急，能见度非常低，船只很难被人发现。幸运的是，在这艘船的附近有一座灯塔，灯塔上的观察员及时发现了这一险情。请你想一想，观察员会做些什么呢？

生：向救援中心报告船只所在的位置，请求救援。

师：对。今天，我们就在这里成立海上救援指挥中心，你们都是指挥中心的指挥官。下面，我们要根据灯塔上观察员发出的信号，准确找到这艘船的位置，实施救援行动，你们准备好了吗？

生：准备好了！

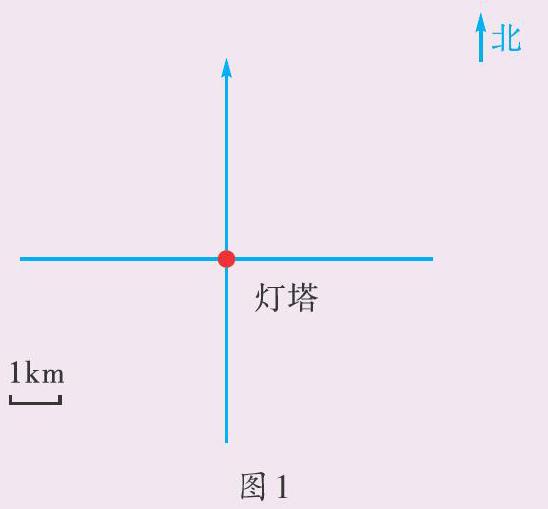
师：现在，我们的首要目标是确定这艘船的位置。（板书课题“确定位置”，课件演示平面图，如图1）

师：在这幅平面图中，以谁为观测点？图中的1厘米代表实际距离多长？

生：以灯塔为观测点，图中1厘米代表实际距离1千米。

【评析】一個贴近生活实际的情境，能够拉近学生与学习内容之间的距离。因此，围绕学习内容设置的教学情境要贴近生活，要有一定的代入感，使学生能够快速进入学习状态。

二、思考交流，解决问题

师：情况十分紧急，听，观察员发来了一个信号。（播放语音“距灯塔3千米”）

师：故障船可能在哪里？赶快在图中画一画。

生画图。

师：都画好了吗？

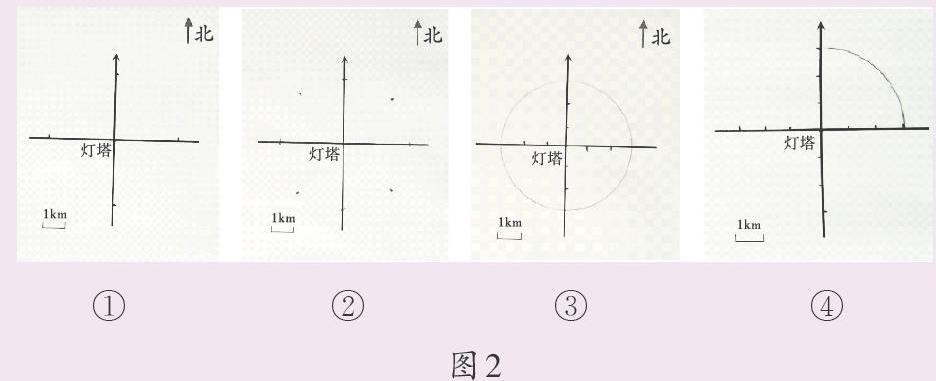
生1：1厘米代表实际距离1千米，3千米应该画3厘米，故障船可能在东、南、西、北这四个方向，所以我画了4个点。（如图2中的①号图）

生2：我认为故障船可能在东南、东北、西南、西北这些地方，所以我画了8个点。（如图2中的②号图）

师：还有别的可能性吗？

生3：我认为有无数种可能，但都集中在一个以灯塔为中心，距离灯塔3千米的圆上，所以我画了一个圆。（如图2中的③号图）

师：时间紧迫！我们只有一次救援机会，现在我们的救援船只可以出发了吗？

生：不能，我们还需要更准确地确定船只的位置。

师：快听！信号员又发来信号了。（播放语音“东北方向”）

生继续画图，修正船只所在的位置。

师：东北方向3千米，现在能确定船只的具体位置了吗？

生：还是不行。

师：方向和距离都有了，怎么还不能确定船只的位置呢？

生1：东北方向表示的是东和北之间的一块区域，是一个大致的方向。

生2：只能确定船只在东北区域的这条弧线上。（如图2中的④号图）

师：虽然现在仍然不能确定船只的位置，但是船只所在的范围缩小了。要确定船只的具体位置，还需要什么信息？

生：角度。

师：来看下一条信息是不是我们想要的。（播放语音“30度”）真的是角度，赶快在图中画出船只的位置吧！

生画图，修正船只所在的位置。

师：找到船只的具体位置了吗？

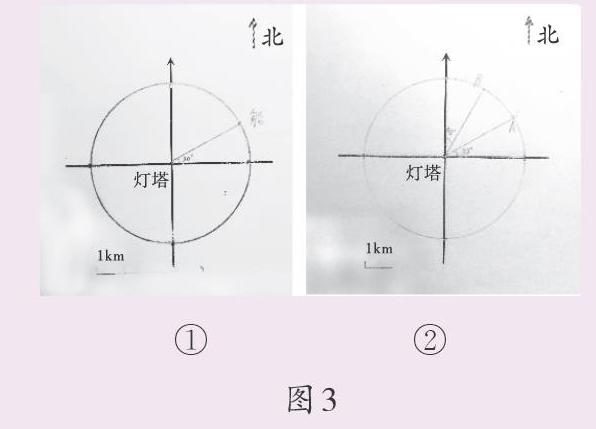
生1：找到了。我用量角器在东北方向量出了30°的角，找到了角与弧线的交点，也就是船只所在的位置。（如图3中的①号图）

2：我找到了两个点，因为东北方向内有两个夹角是30°，一个是从东往北的30°，一个是从北往东的30°，这样一来，还是不能确定故障船只的位置。（如图3中的②号图）

师：大家的意见和他一样吗？只有东北方向30°这个条件还不能确定船只的具体位置，但是把原来的一条弧线缩小到了两个点呢？时间紧迫，让我们一起来祈祷生命的电波。（播放语音“东偏北”）现在能确定船只在哪个点上了吗？

生：能。

师：东偏北是什么意思？

生：东偏北30°，就是以东为基准，向北偏30°，测量的时候把量角器的0刻度线对准正东方向。

师：那么另一个点在什么方向呢？

生：北偏东30°，就是以北为基准，向东偏30°，测量的时候要把量角器的0刻度线对准正北方向。

师：你能准确地描述船只的位置并通知你的船员吗？同桌之间说一说。

生1：船只在灯塔的东北方向，东偏北30°，3千米处。

生2：船只在灯塔的东偏北30°方向，3千米处。

师：语音提示给了4条信息，你为什么只用3条信息呢？

生：东偏北其实包含了东北方向，东偏北30°方向的描述更精确。

师：厉害！这名同学不仅准确地描述出船只的位置，还能辨别多余的信息。在数学上，我们通常说船只在灯塔的东偏北30°方向，3千米处。那么，救援船只现在可以出发了吗？

生：可以了！（播放救援成功的视频画面）

师：4段生命电波，加上同学们的集体智慧，我们救回了故障船上船员们的生命，这就是数学的力量！为我们这些优秀的指挥官鼓鼓掌吧！

师：回顾刚才我们确定船只位置的过程，从一个圆上的无数个点精确到东北区域内的2个点，再精确到1个点。大家想一想，确定位置需要哪些条件？

生：方向、角度、距离。

师：对！这就是确定位置所必需的条件。最后提醒大家，不要漏掉了观测点——灯塔，知道为什么吗？

生：没有观测点，就算描述得再精确，我们也不知道从哪里进行观测。

【评析】奥苏泊尔说：“影响学生学习最重要的因素是学生已经知道了什么。”因此，执教者基于学生视角和“最近发展区”理论设计学习任务。学生在学习过程中，围绕“如何确定船只的具体位置”这一问题不断探索，缩小船只所在的范围，在修正中实现聚焦，经历了从面到线（圆弧）再到点的过程，逐步明白方向、角度、距離和观测点在确定位置中的必要性。这种体验式的数学学习，其实是对数学信息的不断丰富、完善和加工，最终得出结论。整个过程充满理性的思考和分析，散发出浓浓的数学味。

三、巩固提升，深化理解

师：巨大的风浪过去了，大海回归平静。观察员发现的船只越来越多，我们一起来看一看。

（一）巩固练习.

【评析】有效的练习在学生的“最近发展区”里进行才能发挥最大的功效。执教者设计练习题不仅要考虑各个知识点的连贯性，还要注重题目的开放性，以促进学生思维的发展。通过做习题和课件演示，学生明晰了“方向（角度）、距离”之间的相互依存关系，知道每个要素在精确定位过程中的作用，以及在描述位置时方向（角度）的相对性。执教者设计的习题分层递进、逐步深入，对学生巩固所学知识具有重要作用。

（二）生活中的“确定位置”（课件演示“1点钟方向”，如图4）

师：1点钟方向其实包含了方向、角度，像这种描述的方法在军事题材的电影、电视以及户外探险时比较常见。（课件演示“军事题材电影中对1点钟方向的运用”）

生：我想到钟面上1点钟和12点钟之间的夹角是30°，12点指向正北方向，所以就是北偏东30°方向。

师：你觉得电影里出现的1点钟方向一定是北偏东30°方向吗？

生：不一定，因为在实际运用中我们往往以面对的方向作为12点钟方向，而不是去找正北方向。

【评析】数学源于生活。我们在生活中常常借用时钟的时针描述物体的方向，学生在辨析中用数学知识解释了生活中“1点钟方向”，感受到生活语言的简洁性、相对性，体验到了数学语言的严谨性。

（三）深化理解

师：船5在灯塔的南偏西方向，想一想，船5可能在哪里？如果在南偏西45°，船5可能在哪里？如果在南偏西45°方向5千米，你能找到船5的具体位置吗？（课件演示“回顾确定位置的过程”，如图5）

师：回顾刚才确定船5位置的过程，有南偏西这个条件，我们能确定一个面，加上角度这个条件，能确定一条线，再加上距离这个条件，就能确定一个点，其实，确定位置的方法就是不断地获取条件且逐步精确的过程。

【评析】执教者引导学生回顾和梳理确定位置的过程，有利于学生深入理解方向（角度）、距离在确定位置中的意义，逐步从学习数学知识走向掌握数学方法。

四、回顾与延伸

师：同学们，有关确定位置的知识，我们在一年级就已经接触了，现在我们来回顾一下。（微课播放视频“知识回顾”，如图6）

知识点1：一年级时，我们学习了用“第几”的方法在一条直线上确定位置，这时只需要知道一个量。

知识点2：五年级上学期，我们学习了用数对的方法确定位置，需要知道物体在第几行、第几列这两个量。

知识点3：今天我们又学习了用含有角度的方向和距离确定位置。想一想，这两种方法有什么共同之处呢？其实它们都是在一个平面上确定物体的位置，都需要两个量。

小结：这些知识是我们将来学习平面直角坐标系、空间坐标系的基础。请同学们思考，当我们需要在一个空间确定位置时，需要知道几个量呢？

生：（猜想）3个、4个、5个……

师：课后，同学们可以围绕这个问题继续探究。

【评析】执教者引导学生回顾小学阶段“图形与位置”板块内容，让学生经历从一维空间到二维空间的认识，并为学习三维空间的知识埋下伏笔。这样做能够为进一步学习平面直角坐标系、极坐标系、空间坐标系奠定基础。

【总评】

在设计教学时，执教者基于课标理念和学生的已有认知，确定教学目标并最终得以落实，具体体现在以下几个方面：

1.感悟知识学习的意义。虽然“按部就班”式的教学不失为一种方法，但从学生学习能力培养角度来说显然不够。在本课中，学生在获取信息、聚焦问题、解决问题的过程中，逐渐明白了方向（角度）、距离在描述物体位置时的作用。学生对于知识的理解已经不仅停留在对教材知识的浅表记忆上，而是逐渐内化为描述位置的一种内在需求。

2.培养学生的空间观念。课标把“空间观念”作为义务教育阶段数学学习的核心概念之一，把建立初步的空间观念作为数学思考的一个重要目标。从某种意义上说，空间观念作为一种重要的教学能力之一，是评价学生能力发展的一项重要指标。学生在目标物体范围不断缩小的过程中，由初始可能的4个点、8个点、圆上无数个点到四分之一圆上的点，然后聚焦到两个点，最终精确到1个点，这不仅培养了学生的空间想象能力，还为本单元的后续学习奠定了思维基础。

3.发展数学思维能力。执教者总结和回顾“确定位置”的学习过程，使学生加深了对方向（角度）、距离在确定位置中所起作用的理解，有助于学生掌握数学学习方法，从而体会到数学学习是一个螺旋上升的过程，是一个循序渐进的过程，更是一个不断拓展丰富的过程。

（该课例获2018年全区中小学信息技术与学科教学深度融合优秀课例观摩评选活动一等奖）

（责编 欧孔群）