柔性绳网展开过程的多元回归模型的优化

王 全， 陈 曦， 石益建， 付 杰

(南京理工大学机械工程学院，南京 210094)

目前，针对柔性绳网系统的研究，主要方法是建立柔性绳网的仿真模型，用于分析其展开过程的动力学特性。Gärdsback等[1]开发了一个解析三自由度模型和一个全三维有限元模型，用以分析折叠后的柔性绳网展开过程的动力学特性。李京阳等[2]建立了空间飞网系统的柔性模型和松弛模型，并进行对比研究，以使模型的动力学特性更逼近于真实飞网。张青斌等[3]基于离散化模型，研究了柔性绳网展开过程中展开面积、空间位形和飞行距离等方面的动力学机理。刘海涛等[4]基于正交试验，对柔性绳网展开过程的影响因子进行灵敏度分析。刘昊等[5]利用绝对节点坐标法，建立柔性绳网捕获过程的动力学模型，验证静力学和振动分析提供参数选型的有效性，并分析了影响收口过程的关键指标。甄明等[6]设计了地面环境下的柔性绳网碰撞试验，通过对比试验结果与仿真结果，分析碰撞过程中的碰撞力和绳段内力，及对包裹目标的影响。

在柔性绳网展开过程中，通常需要柔性绳网在一定距离上展开到最大，但由于柔性绳网仿真中选择的参数无法包含所有的数值，即使进行大量仿真，对比所获得的数据，也无法使该指标达到最佳。Design-Expert可对试验后的数据进行回归分析，拟合多项式曲线，建立拟合因素与响应值间之间的数学模型，并进一步求得最优参数。陶有俊等[7]通过Design-Expert中的 Box-Behnken 试验设计粉煤灰摩擦电选脱炭试验方案，二次方修正模型，并以脱炭效率为优化指标，得到最佳试验条件。Qian等[8]针对软土加固，利用Box-Behnken试验方法，设计室内无侧限抗压强度试验，并获得高炉渣、石膏、激发剂CaO的最佳配比。

图1所示为柔性绳网示意图，现采用集中质量阻尼弹簧[3]建立柔性绳网的动力学模型，并由Design-Expert 11软件设计仿真方案，进而获得充足的仿真数据，同时建立展开位移和展开面积的多元回归模型，此外，对多元回归模型进行优化，得到满足设计标准的理想参数组合，以及讨论发射速度和旋转角对展开效果的影响。

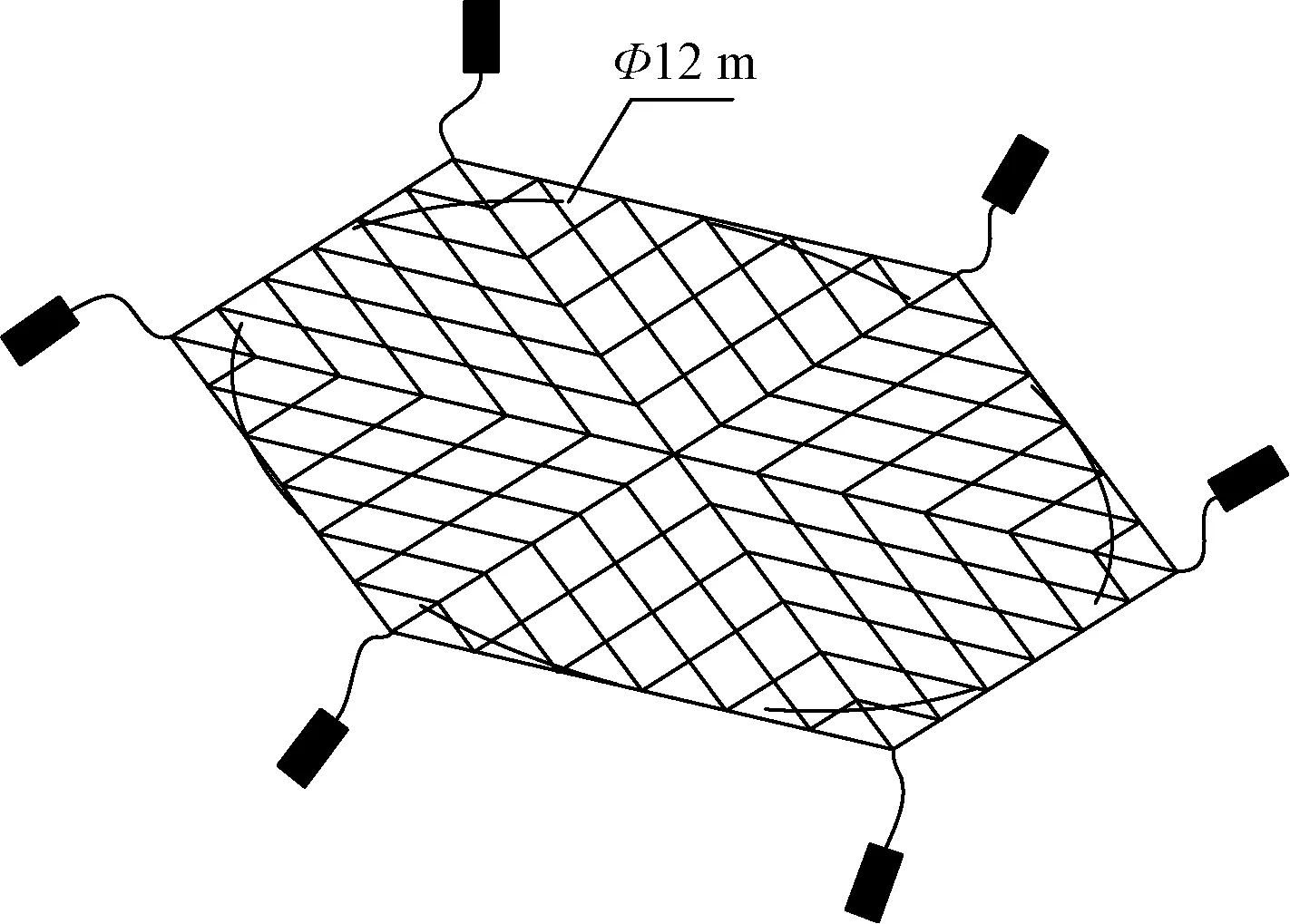
图1 柔性绳网示意图

1 动力学模型

采用离散化思路，将柔性绳网离散为一系列节点，相连两节点仅考虑张力与阻尼力，且柔性绳网质量均匀分配到所有节点上，即将柔性绳网处理为大量集中质量阻尼弹簧的组合，如图2所示。

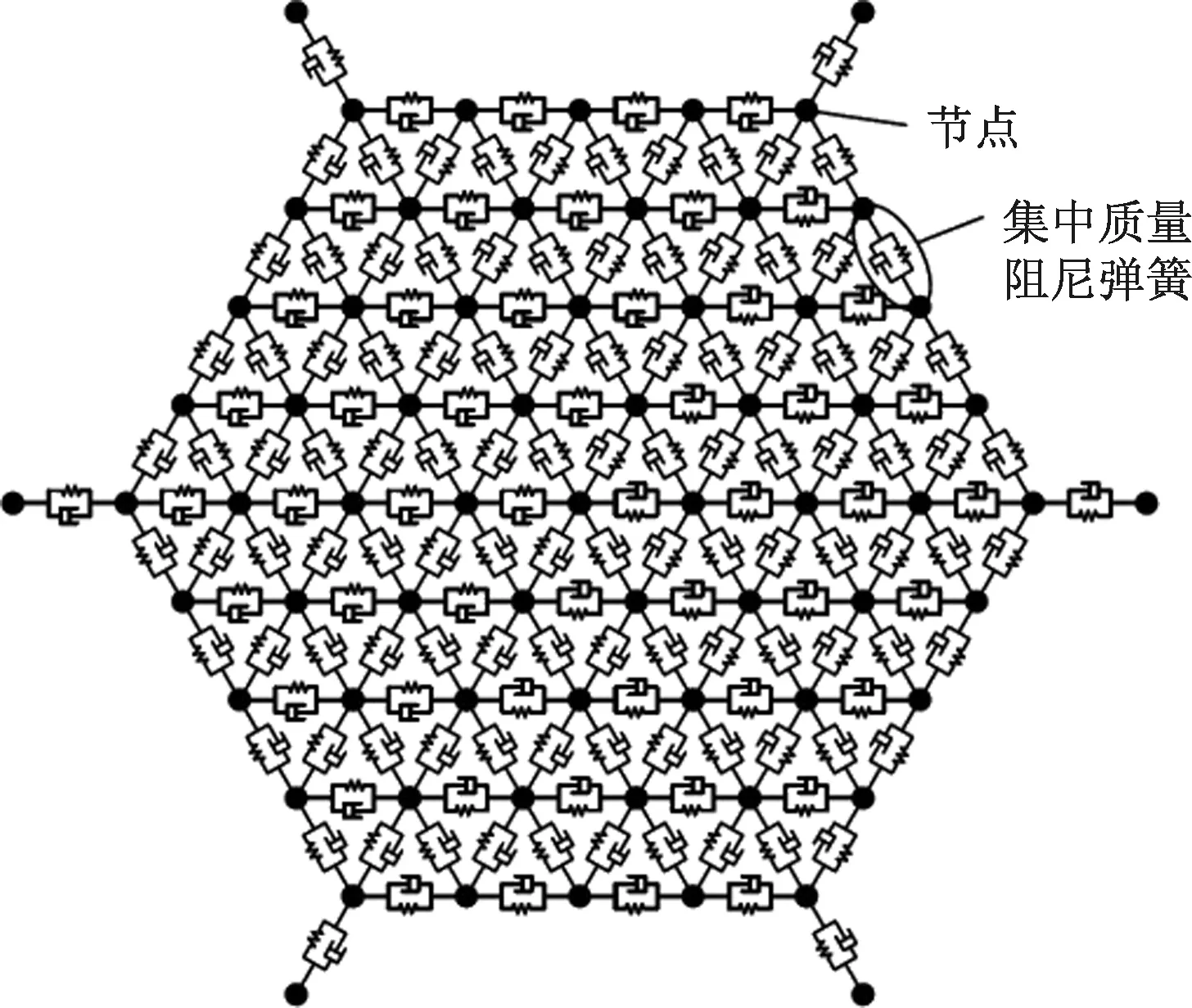
图2 柔性绳网离散化示意图

柔性绳网离散后任一节点的运动公式为

(1)

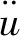
中央差分法是一种常用的显式时间积分方法，经常用于求解运动公式[9]，由中央差分法可得：

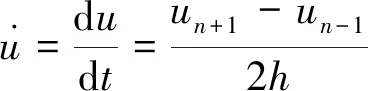
(2)

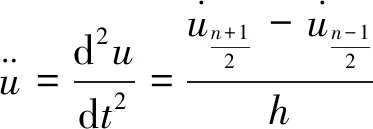
(3)

将式(3)代入式(1)，可得位移迭代公式为

(4)

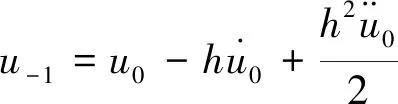
(5)

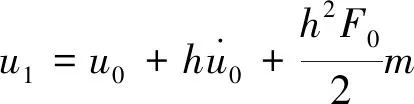
(6)

2 多元回归模型

2.1 仿真设计

响应曲面法是正交试验的一种常用方法，将给定的数据拟合为多元二次回归方程，表示影响因子与响应值之间关系[10]。柔性绳网展开过程中的研究对象为展开面积与展开距离，其主要影响因子为发射速度V、旋转角α和时间t，同时各影响因子的取值范围为：发射速度10～30 m/s，旋转角10°～22° ，时间1～1.4 s，最后按正交表对各影响因子进行排序，并进行水平编码，其值见表1。

通过C++编制柔性绳网动力学模型的计算程序，并将表1中各影响因子数值带入进行仿真，得到50组仿真数据，其部分数据见表2。

表1 三因子五水平编码

表2 部分仿真数据

2.2 响应模型选择

影响因子与响应值之间的多元二次回归公式可以表示为

(7)

式(7)中：y为响应值，即展开位移L和展开面积S；xi为影响因子，即发射速度V、旋转角α和时间t；bi是第i个影响因子的线性影响系数；bii是第i个影响因子的非线性影响系数；bij是第i、j两个影响因子交互作用的非线性影响系数；k为影响因子的个数，k=3。

实验数据采用软件Design-Expert 11进行分析[11-12]，应用多重模型对仿真数据进行拟合，得到展开位移L和展开面积S各响应模型R2综合分析和方差分析比较见表3～表6。由表3～表6综合分析可得，展开位移L最优的响应模型是二次方程模型，展开面积S最优的响应模型是2FI模型。

表3 R2综合分析(展开位移)

表4 方差分析比较(展开位移)

表5 R2综合分析(展开面积)

表6 方差分析比较(展开面积)

注：R2表示决定系数；vs表示对比；F表示拟合缺陷；prob表示概率。

2.3 显著性分析及多元回归模型建立

展开位移L和展开面积S及其影响因子的显著性分析[13]，见表7和表8。P用于表示对模型影响的显著性，由表7可知，展开位移L模型的F为5 115.04，对应的P<0.000 1，说明展开位移L的回归方程为最高显著：发射速度V、旋转角α、时间t、发射速度和旋转角的交互(Vα)、发射速度和时间的交互(Vt)以及发射速度平方项(V2)呈最高显著，说明这些项对展开位移L起主要影响作用；旋转角和时间的交互(αt)、旋转角平方项(α2)以及时间平方项(t2)显著性较小，对展开位移L的影响较小。

由表8可知，展开面积S模型的F=154.06，对应的P<0.000 1，说明展开面积S的回归方程为最高显著：发射速度V、旋转角α、时间t以及发射速度和旋转角的交互(Vα)呈最高显著，说明这些项对展开面积S起主要影响作用；旋转角和时间的交互(αt)以及发射速度和时间的交互(Vt)显著性较小，对展开面积S的影响较小。

表7 展开位移L及其影响因子的显著性分析

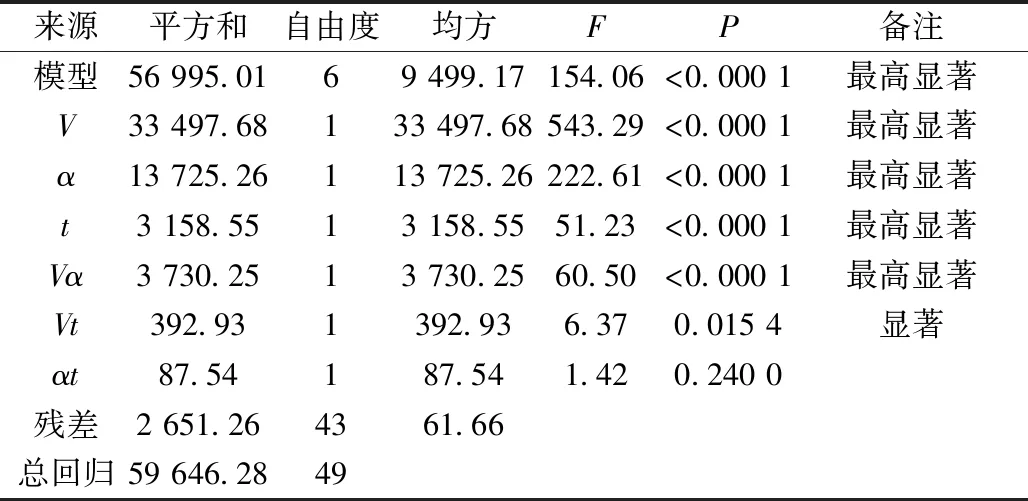
表8 展开面积S及其影响因子的显著性分析

展开位移L和展开面积S对应的多元回归模型如式(8)、式(9)所示。

L=-7.706 05+0.075 362V-0.078 992α-

1.954 23t+0.008 589Vα+0.769 141Vt+

0.137 111αt-0.003 757V2-0.003 995α2+

0.239 183t2

(8)

S=45.503 59-4.728 79V-4.937 79α-

38.936 54t+0.312 435Vα+3.042 06Vt+

2.393 17αt

(9)

2.4 多元回归模型验证

为了验证多元回归模型的准确性，进行了8个仿真验证，并为下面的优化提供仿真依据。这 8个仿真验证中各影响因子的取值与表1中的五水平数值不同，但取值均位于正交试验各影响因子的数值范围内，其具体取值见表9。

由表9可知，展开位移L和展开面积S对应的多元回归模型的计算结果与仿真结果的误差均在10%以内，说明多元回归模型的可信度较高，其优化分析结果可靠。

表9 多元回归模型的仿真验证

注：展开位移L和展开面积S为仿真值，展开位移计算值L′和展开面积计算值S′为式(8)、式(9)的计算结果。

3 模型优化结果与讨论

3.1 数值优化

基于以上多元回归模型，软件Design-Expert 11可以对各影响因子进行优化，即在保证展开位移L在一定范围内，展开面积S达到最大值时的各个影响因子的取值，具体优化条件见表10。

表11为按照表10中的优化条件进行优化所得到的柔性绳网展开优化方案。由优化结果可知，当发射速度为29.481～30.000 m/s、旋转角度为21.916°～22°和展开时间为1.092～1.115 s 时，可以得到展开位移为19.824～20.000 m 和展开面积为115.741～116.644 m2的较好展开效果。

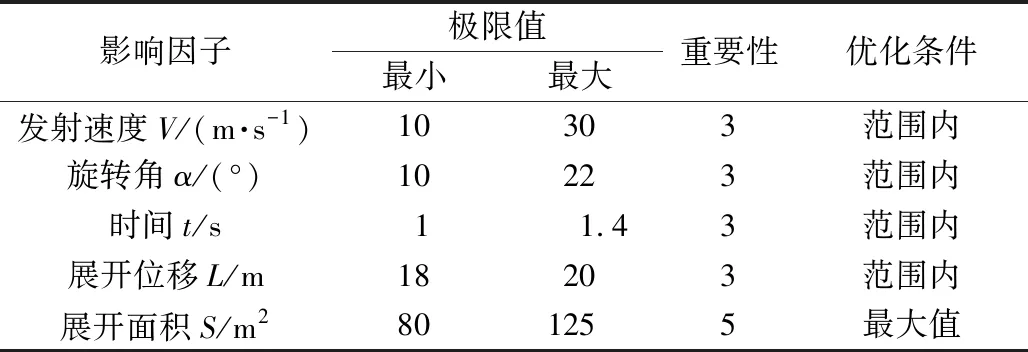
表10 优化条件

表11 柔性绳网展开优化方案

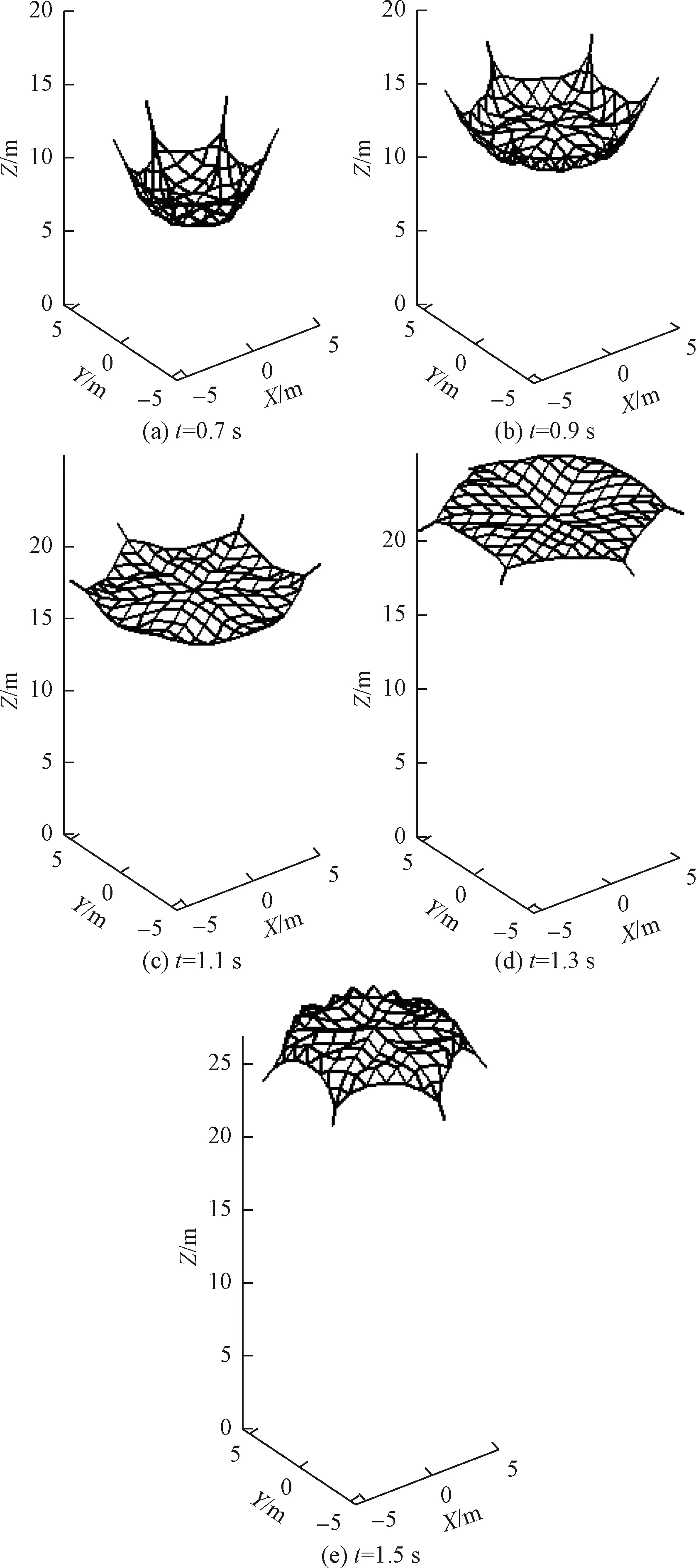
图3 柔性绳网展开过程(V=30 m/s，α=21.916°)

从以上10组柔性绳网展开优化方案中，选取第5组参数V=30 m/s和α=21.916° 进行仿真，得到柔性绳网展开过程示意图以及展开面积S随展开位移L和时间t的变化图，如图3、图4所示。由图3、图4可知，在t=0～1.1 s内，柔性绳网逐渐展开，当t=1.1 s 时，展开位移仿真值L′=19.85 m ，展开面积仿真值S′=115.8 m2，此时柔性绳网在优化条件下展开效果最好，当t继续增加时，柔性绳网逐渐张开到最大，之后由于自身张力和惯性作用，外围逐渐向中心收缩，展开面积S逐渐减小，但由于展开位移L>20 m ,超出优化条件范围，不满足设计要求。由此可知，在给定的设计方案下，通过软件Design-Expert 11，多元回归模型能够得到较为准确理想的优化方案。

图4 展开面积S随展开位移L和时间t的变化图

3.2 图形优化

图5(a)～图5(d)所示为不同发射速度条件下所获得的旋转角和展开时间的最佳匹配图，随着发射速度从30 m/s变化到21.8 m/s,最佳匹配区域从右下角逐渐移动到右上角，展开位移L=18 m、20 m 和展开面积S=80 m2、125 m2四条边界线均上移，以及四条边界线逐渐消失，整个区域面积大小首先近似保持不变，之后逐渐变小，最终消失。这是由于发射速度减小，相同旋转角条件下到达展开位移L=10、15 m 以及展开面积S=80 m2、115 m2所需的展开时间增加，因而最佳匹配区域以及A、B、C和D四条边界线向上移动，当A、B边界线都在取值范围内时，最佳匹配区域由边界线A、B、C及α=22° 构成，面积近似保持不变，当B边界线不在取值范围内时，最佳匹配区域面积逐渐变小，当A、B边界线不在取值范围内时，最佳匹配区域消失，即发射速度V减小到21.8 m/s及以下时, 没有达到优化条件的参数组合。

图5(e)～图5(h)所示为不同旋转角条件下所获得的发射速度和展开时间的最佳匹配图，随着旋转角从22° 变化到16.2°，A和B边界线变化较小，C和D边界线逐渐上移，最佳匹配区域面积逐渐减少，起初为倾斜带状区域，之后逐渐消失。随着旋转角的逐渐变小，相同发射速度的条件下到达展开面积S=80 m2、115 m2需的展开时间增加，因而C、D边界线逐渐上移，由于旋转角在给定值范围内对展开位移L影响较小，因而A、B边界线变化较小。由C、D与A、B边界线变化可知，区域面积逐渐减少，并且旋转角减小到16.2° 及以下时，最佳匹配区域消失，即没有达到优化条件的参数组合。

A为展开位移L=18 m；B为展开位移L=20 m；C为展开面积S=80 m2；D为展开面积S=125 m2

4 结论

采用Design-Expert 11软件对柔性绳网展开过程中的展开位移和展开面积的研究进行设计、结果分析和优化，得到以下结论。

(1)通过仿真验证所建立的多元回归模型的准确性，模型计算结果与仿真结果的误差均在10%以内，说明多元回归模型进行优化分析，其结果较为可靠。

(2)当发射速度为29.481～30.000 m/s、旋转角度为21.916°～22°和展开时间为1.092～1.115 s时，可以得到展开位移为19.824～20.000 m和展开面积为115.741～116.644 m2的较好展开效果。

(3)优化分析结果表明，发射速度越小和旋转角越小，则最佳匹配区域中的参数组合越少；当发射速度V<21.8 m/s或旋转角α<16.2° 时，最佳匹配区域消失，没有参数组合达到优化条件。